广东省广州市番禺中学2024-2025学年下学期八年级期中数学试卷(含答案)
文档属性
| 名称 | 广东省广州市番禺中学2024-2025学年下学期八年级期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 13:45:14 | ||
图片预览

文档简介
2024-2025学年广东省广州市番禺中学
八年级(下)期中数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.下列各组数中能作为直角三角形的三边长的是( )
A. 1,1,2 B. 2,3,4 C. 4,5,6 D. 8,15,17
3.下列曲线中,能表示y是x的函数的是( )
A. B.
C. D.
4.一次函数的图象经过的象限是( )
A. 一,二,三 B. 二,三,四 C. 一,二,四 D. 一,三,四
5.如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是( )
A. , B. ,
C. , D. ,
6.如图,的直角边OA与数轴重合,,以点O为圆心,OB长为半径作弧,与数轴交于点C,则点C表示的数为( )
A. 10 B. C. D.
7.如图,菱形ABCD的对角线交于点O,点M为AB的中点,连接若,,则OM的长为( )
A.
B. 4
C. 5
D.
8.已知,则的值为( )
A. 2 B. 1 C. 0 D.
9.同一平面直角坐标系中,一次函数与为常数的图象可能是( )
A. B.
C. D.
10.如图,在矩形ABCD中,,的平分线交BC于点E,,垂足为H,连接BH并延长,交CD于点F,DE交BF于点有下列结论:①≌;②;③;④;其中正确的是( )
A. ①③④ B. ①②④ C. ①②③ D. ②③④
二、填空题:本题共6小题,每小题3分,共18分。
11.直线向下平移3个单位,得到的直线的表达式是______.
12.如图所示的三角形为直角三角形,那么字母A所表示的正方形的边长等于______.
13.若直线经过点,则代数式的值是______.
14.若是关于x的一次函数,则m的值为______.
15.若代数式有意义,则实数x的取值范围是______.
16.如图,正方形ABCD与正的顶点A重合,将绕其顶点A旋转,在旋转过程中,当时,的大小可以是______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题4分
计算:
18.本小题4分
请通过列表、描点、连线在平面直角坐标系中画出函数的图象.
19.本小题6分
如图,在四边形ABCD中,,,,,且求的度数.
20.本小题6分
如图所示为某汽车行驶的路程与时间的函数关系图象,观察图象中所提供的信息解答下列问题:
汽车前9分钟的平均速度是多少?
汽车中途停了多长时间?
汽车后14分钟的平均速度是多少?
21.本小题8分
如图,E,F是四边形ABCD的对角线AC上两点,,,求证:
≌;
四边形ABCD是平行四边形.
22.本小题10分
如图,菱形ABCD的对角线AC与BD相交于点O,CD的中点为E,连接OE并延长至点F,使得,连接CF,
求证:四边形OCFD是矩形;
若,,求菱形ABCD的面积.
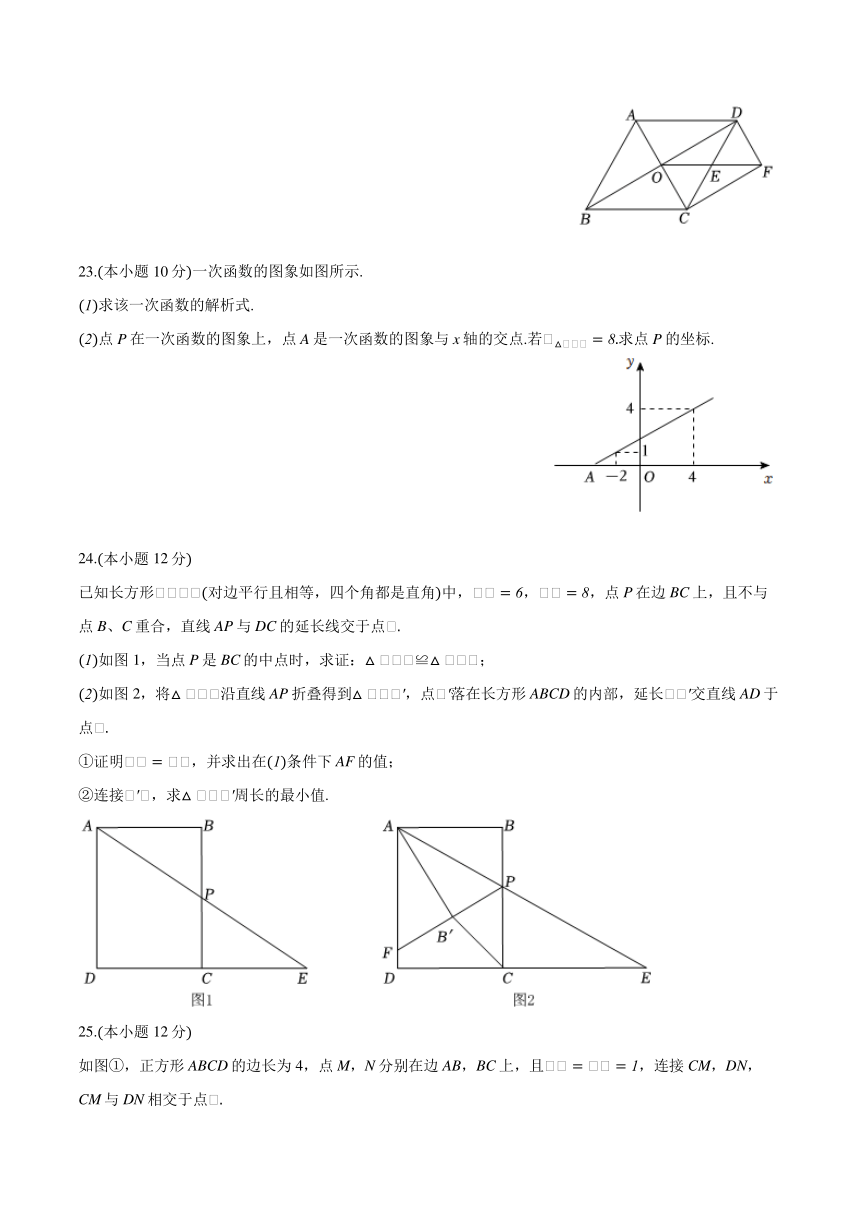
23.本小题10分一次函数的图象如图所示.
求该一次函数的解析式.
点P在一次函数的图象上,点A是一次函数的图象与x轴的交点.若求点P的坐标.
24.本小题12分
已知长方形对边平行且相等,四个角都是直角中,,,点P在边BC上,且不与点B、C重合,直线AP与DC的延长线交于点
如图1,当点P是BC的中点时,求证:≌;
如图2,将沿直线AP折叠得到,点落在长方形ABCD的内部,延长交直线AD于点
①证明,并求出在条件下AF的值;
②连接,求周长的最小值.
25.本小题12分
如图①,正方形ABCD的边长为4,点M,N分别在边AB,BC上,且,连接CM,DN,CM与DN相交于点
线段CM与DN之间的数量关系是______,位置关系是______;
如图②,若E,F分别是DN与CM的中点,求EF的长;
如图③,延长CM至点P,连接BP,使求线段PM的长.
答案
1.B
2.D
3.A
4.C
5.C
6.D
7.A
8.B
9.B
10.A
11.
12.
13.2
14.
15.且
16.或
17.解:
根据平方差公式进行计算即可.
本题考查了二次根式的混合运算,解题的关键是根据运算法则和公式法来计算.
18.解:当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
列表:如表是x与y的对应值:
x … 0 1 2 …
y … 0 2 4 6 …
描点并画出该函数的图象:
.
19.解:在中,
根据勾股定理:,
在中,,,
,
为直角三角形,
20.解:由函数图象知前9分钟汽车行驶了12千米,
所以汽车前9分钟的平均速度是千米/分钟;
由函数图象知时,汽车行驶的路程保持12千米不变,
汽车中途停了分钟;
由函数图象知汽车后14分钟行驶的路程为千米,
汽车后14分钟的平均速度是千米/分钟.
21.证明:,
在和中,
,
≌;
由知≌,
,,
四边形ABCD是平行四边形.
22.证明:的中点为E,
,
连接OE并延长至点F,,
四边形OCFD是平行四边形,
四边形ABCD是菱形,对角线AC与BD相交于点O,
,
,
四边形OCFD是矩形.
解:,,
,,
,
,
,
,
菱形ABCD的面积为
23.解:设一次函数解析式为,
一次函数图象过点和,
,解得
所以一次函数解析式为;
把代入,
得,解得,
点坐标为,
设P点坐标为,
,
,
,解得,
点坐标为或
24.证明:四边形ABCD是矩形,
,
,,
点P是BC的中点,
,
≌;
解:①四边形ABCD是矩形,
,
,
由折叠得,
,
,
矩形ABCD中,,,
,
点P是BC的中点,
,
由折叠得,,,
设,则,
,
在中,,
,
解得,
即;
②由折叠得,,
的周长,
连接,AC,
,
当点恰好位于对角线AC上时,最小,
在中,,,
,
的最小值,
周长的最小值
25.解:,且,
理由:四边形ABCD是正方形,
在和中,
,
≌,
,,
,
,
,
,
线段CM和DN的关系为:,且,
故答案为:,;
连接CE并延长交AD于G,连接GM,
四边形ABCD是正方形,
,,,
,
在和中,
,
≌,
,,
又,
,
正方形的边长为4,,
,
在中,由勾股定理得:,
,
,
;
如图3,过点B作于点H,
,
,
,
,
,
,
,
,
八年级(下)期中数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.下列各组数中能作为直角三角形的三边长的是( )
A. 1,1,2 B. 2,3,4 C. 4,5,6 D. 8,15,17
3.下列曲线中,能表示y是x的函数的是( )
A. B.
C. D.
4.一次函数的图象经过的象限是( )
A. 一,二,三 B. 二,三,四 C. 一,二,四 D. 一,三,四
5.如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是( )
A. , B. ,
C. , D. ,
6.如图,的直角边OA与数轴重合,,以点O为圆心,OB长为半径作弧,与数轴交于点C,则点C表示的数为( )
A. 10 B. C. D.
7.如图,菱形ABCD的对角线交于点O,点M为AB的中点,连接若,,则OM的长为( )
A.
B. 4
C. 5
D.
8.已知,则的值为( )
A. 2 B. 1 C. 0 D.
9.同一平面直角坐标系中,一次函数与为常数的图象可能是( )
A. B.
C. D.
10.如图,在矩形ABCD中,,的平分线交BC于点E,,垂足为H,连接BH并延长,交CD于点F,DE交BF于点有下列结论:①≌;②;③;④;其中正确的是( )
A. ①③④ B. ①②④ C. ①②③ D. ②③④
二、填空题:本题共6小题,每小题3分,共18分。
11.直线向下平移3个单位,得到的直线的表达式是______.
12.如图所示的三角形为直角三角形,那么字母A所表示的正方形的边长等于______.
13.若直线经过点,则代数式的值是______.
14.若是关于x的一次函数,则m的值为______.
15.若代数式有意义,则实数x的取值范围是______.
16.如图,正方形ABCD与正的顶点A重合,将绕其顶点A旋转,在旋转过程中,当时,的大小可以是______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题4分
计算:
18.本小题4分
请通过列表、描点、连线在平面直角坐标系中画出函数的图象.
19.本小题6分
如图,在四边形ABCD中,,,,,且求的度数.
20.本小题6分
如图所示为某汽车行驶的路程与时间的函数关系图象,观察图象中所提供的信息解答下列问题:
汽车前9分钟的平均速度是多少?
汽车中途停了多长时间?
汽车后14分钟的平均速度是多少?
21.本小题8分
如图,E,F是四边形ABCD的对角线AC上两点,,,求证:
≌;
四边形ABCD是平行四边形.
22.本小题10分
如图,菱形ABCD的对角线AC与BD相交于点O,CD的中点为E,连接OE并延长至点F,使得,连接CF,
求证:四边形OCFD是矩形;
若,,求菱形ABCD的面积.
23.本小题10分一次函数的图象如图所示.
求该一次函数的解析式.
点P在一次函数的图象上,点A是一次函数的图象与x轴的交点.若求点P的坐标.
24.本小题12分
已知长方形对边平行且相等,四个角都是直角中,,,点P在边BC上,且不与点B、C重合,直线AP与DC的延长线交于点
如图1,当点P是BC的中点时,求证:≌;
如图2,将沿直线AP折叠得到,点落在长方形ABCD的内部,延长交直线AD于点
①证明,并求出在条件下AF的值;
②连接,求周长的最小值.
25.本小题12分
如图①,正方形ABCD的边长为4,点M,N分别在边AB,BC上,且,连接CM,DN,CM与DN相交于点
线段CM与DN之间的数量关系是______,位置关系是______;
如图②,若E,F分别是DN与CM的中点,求EF的长;
如图③,延长CM至点P,连接BP,使求线段PM的长.
答案
1.B
2.D
3.A
4.C
5.C
6.D
7.A
8.B
9.B
10.A
11.
12.
13.2
14.
15.且
16.或
17.解:
根据平方差公式进行计算即可.
本题考查了二次根式的混合运算,解题的关键是根据运算法则和公式法来计算.
18.解:当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
当时,;
列表:如表是x与y的对应值:
x … 0 1 2 …
y … 0 2 4 6 …
描点并画出该函数的图象:
.
19.解:在中,
根据勾股定理:,
在中,,,
,
为直角三角形,
20.解:由函数图象知前9分钟汽车行驶了12千米,
所以汽车前9分钟的平均速度是千米/分钟;
由函数图象知时,汽车行驶的路程保持12千米不变,
汽车中途停了分钟;
由函数图象知汽车后14分钟行驶的路程为千米,
汽车后14分钟的平均速度是千米/分钟.
21.证明:,
在和中,
,
≌;
由知≌,
,,
四边形ABCD是平行四边形.
22.证明:的中点为E,
,
连接OE并延长至点F,,
四边形OCFD是平行四边形,
四边形ABCD是菱形,对角线AC与BD相交于点O,
,
,
四边形OCFD是矩形.
解:,,
,,
,
,
,
,
菱形ABCD的面积为
23.解:设一次函数解析式为,
一次函数图象过点和,
,解得
所以一次函数解析式为;
把代入,
得,解得,
点坐标为,
设P点坐标为,
,
,
,解得,
点坐标为或
24.证明:四边形ABCD是矩形,
,
,,
点P是BC的中点,
,
≌;
解:①四边形ABCD是矩形,
,
,
由折叠得,
,
,
矩形ABCD中,,,
,
点P是BC的中点,
,
由折叠得,,,
设,则,
,
在中,,
,
解得,
即;
②由折叠得,,
的周长,
连接,AC,
,
当点恰好位于对角线AC上时,最小,
在中,,,
,
的最小值,
周长的最小值
25.解:,且,
理由:四边形ABCD是正方形,
在和中,
,
≌,
,,
,
,
,
,
线段CM和DN的关系为:,且,
故答案为:,;
连接CE并延长交AD于G,连接GM,
四边形ABCD是正方形,
,,,
,
在和中,
,
≌,
,,
又,
,
正方形的边长为4,,
,
在中,由勾股定理得:,
,
,
;
如图3,过点B作于点H,
,
,
,
,
,
,
,
,
同课章节目录
