广东省珠海市华发教育2024-2025学年八年级下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 广东省珠海市华发教育2024-2025学年八年级下学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 14:01:58 | ||
图片预览




文档简介
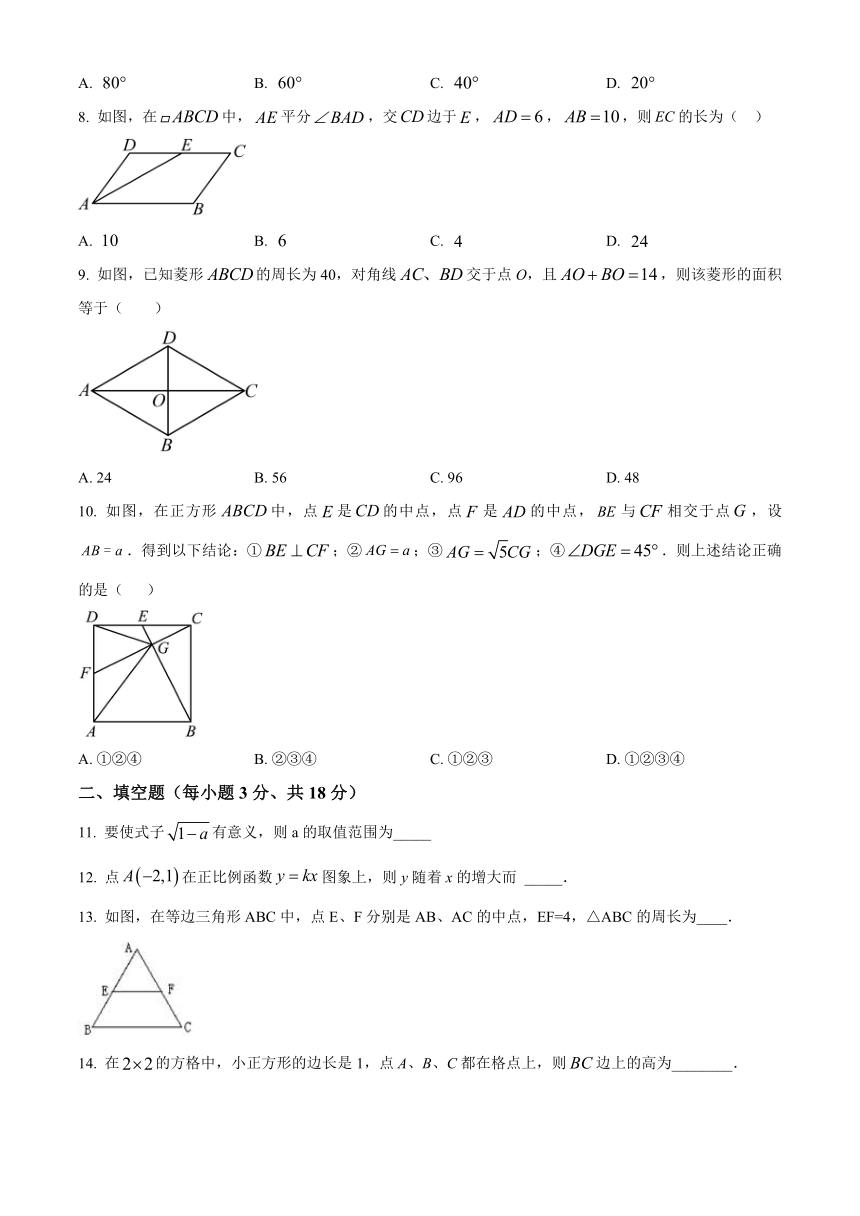
华发教育初中2024-2025学年第二学期义务教育阶段质量检测
八年级数学
一、选择题(每小题3分、共30分)
1. 下列曲线中,表示y是x的函数的是 ( )
A. B.
C. D.
2. 司机王师傅在加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B. 数量 C. 单价 D. 金额和数量
3. 下列二次根式中,为最简二次根式的是( )
A. B. C. D.
4. 已知在中,且,,则( )
A. 5 B. C. 5或 D. 或
5. 下列各组数中,能作为直角三角形三边长的是( )
A. 4,5,6 B. 5,8,13 C. 1,1, D. 1,,4
6. 下列计算正确的是( )
A. B.
C. D.
7. 在平行四边形中,如果,那么等于( )
A. B. C. D.
8. 如图,在中,平分,交边于,,,则的长为( )
A. B. C. D.
9. 如图,已知菱形的周长为40,对角线交于点O,且,则该菱形的面积等于( )
A. 24 B. 56 C. 96 D. 48
10. 如图,在正方形中,点是的中点,点是的中点,与相交于点,设.得到以下结论:①;②;③;④.则上述结论正确的是( )
A. ①②④ B. ②③④ C. ①②③ D. ①②③④
二、填空题(每小题3分、共18分)
11. 要使式子有意义,则a的取值范围为_____
12. 点在正比例函数图象上,则y随着x的增大而 _____.
13. 如图,在等边三角形ABC中,点E、F分别是AB、AC的中点,EF=4,△ABC的周长为____.
14. 在的方格中,小正方形的边长是1,点A、B、C都在格点上,则边上的高为________.
15. 如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作分别交AB,BC于E,F两点,,则EF的长为__________.
16. 如图,在矩形中,E为对角线上与不重合的一个动点,过点E作与点F,于点G,连接,若,则的最小值_______.
三、解答题(每小题6分、共18分)
17. 计算:
(1).
(2).
18. 已知正比例函数的图象过点.
(1)写出这个正比例函数的函数解析式;
(2)已知点在这个正比例函数的图象上,求a的值.
19. 如图,在ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)若∠FDB=30°,∠ABC=45°,BC=,求DF的长.
四、解答题(每小题9分、共27分)
20. 如图1,是我国汉代的赵爽用来证明“勾股定理”的“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为、,斜边长为.
(1)图中阴影部分小正方形的面积用两种方法可分别表示为________和________;
(2)若,大正方形的边长,则小正方形的边长为________;
[知识迁移]通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是棱长为的正方体,被如图所示的分割线分成8块.
(3)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为________;
(4)已知,,利用上面的规律求的值.
21. 问题情境:通过对《平行四边形》一章内容的学习,我们认识到矩形、菱形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,还有各自的特殊性质.根据它们的特殊性,得到了这些特殊的平行四边形的判定定理.数学课上,老师给出了一道题:如图①,矩形的对角线,交于点O,过点D作,且,连接.
初步探究:
(1)判断四边形的形状,并说明理由.
深入探究:
(2)如图②,若四边形是菱形,(1)中的结论还成立吗?请说明理由.
拓展延伸:
(3)如图③,若四边形是正方形,四边形又是什么特殊的四边形?请说明理由.
22. 【阅读材料】
在学习正方形时,我们遇到过这样的问题:如图1,在正方形中,点E、F、G、H分别在、、、上,且,垂足为M,那么与相等吗?
分别过点G、H作、,垂足分别为P、Q,通过证明,得到.
根据阅读材料,完成下面探究1、探究2中的问题.
【探究1】
如图2,在正方形中,点E在上,使用无刻度的直尺和圆规作,交于点F(要求直尺、圆规各使用一次),保留作图痕迹,并标出点F,不要求写作法;
【探究2】
如图3,在正方形中,点E、F分别在、上,将正方形沿着翻折,点B、C分别落在、处,且经过点D,将纸片展开,延长交于点G,连接交于点M.
(1)求证:;
(2)求证:.
五、解答题(23题13分、24题14分,共27分)
23. 阅读材料:
中国-西班牙联合发行《中欧班列(义乌-马德里)》特种邮票1套2枚,两枚邮票的大小、形状相同(如图1).邮票在设计时采用了多种数学元素:根据画面内容邮票以平行四边形的形式呈现,代表着列车前进的速度,凸显中欧班列的动态美;中国与西班牙两个列车图形保持对称,并向外延展,凸显中欧班列的和谐美;
在单枚邮票票面上的平行四边形中,邻边与的长度比非常接近黄金分割数.单枚邮票的规格(平行四边形:长边50毫米,短边32毫米,高28毫米)见图2所示.设图1的中边上的高为.
根据以上信息解决问题:
(1)【相关计算】①单枚邮票的面积为:________,周长为:________.
②计算的长为:________(结果用最简二次根式表示);
(2)【特例证明】图1中,求证:四边形是平行四边形.
(3)【数形结合】现在将图1中的设计成标准的黄金平行四边形,也就是满足相邻两边的比为黄金分割数的平行四边形.如图3所示,即在中,两邻边、满足,现又在上取点,且满足,过点作交边于点.求证:四边形是菱形.
24. 综合与实践
数学课上,老师以“矩形的折叠”为主题开展活动.
实践操作:
现有一张矩形纸片.
第一步:如图1,将矩形纸片先沿对角线折叠,得到折痕,然后把纸片展平;
第二步:如图2,将矩形纸片折叠,使点与点重合,得到折痕,然后把纸片展平,与的交点为点,连接.
第三步:如图3,将矩形纸片沿过点的直线折叠,点的对应点为点,点的对应点为点与交于点,然后把纸片展平.
问题解决:
(1)的长为 ;
(2)判断四边形的形状,并说明理由;
拓展探索:
(3)若,求的长.
参考答案
1-10:DCDBC CACCD
减小
24、
17、(1)解:
;
(2)解:
.
18、(1)将代入正比例函数,得
正比例函数的函数解析式为;
(2)由(1)可知,
点在这个正比例函数的图象上,
19、(1)证明:∵CF∥AB,
∴∠ECF=∠EBD.
∵E是BC中点,
∴CE=BE.
∵∠CEF=∠BED,
∴△CEF≌△BED.
∴CF=BD.
∴四边形CDBF是平行四边形.
(2)解:如图,作EM⊥DB于点M,
∵四边形CDBF是平行四边形,BC=,
∴,DF=2DE.
在Rt△EMB中,EM=BE sin∠ABC=2,
在Rt△EMD中,∵∠EDM=30°,
∴DE=2EM=4,
∴DF=2DE=8.
(1);;
(2)3;
;
(4)∵,,,
∴,
∴.
21、解:(1)四边形是菱形
理由如下:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,,,
∴,
所以四边形是菱形 ;
(2)(1)中的结论不成立;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是菱形,
∴,
∴,
∴四边形是矩形
(3)四边形是正方形;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是正方形,
∴,,,,
∴,,
∴四边形是正方形.
22、解∶[探究1]
如图,即为所求,
∵四边形是正方形,
∴,,,
由作图知:,
∴,
∴,
∵,
∴,
∴;
[探究2]
(1)证明:∵翻折,
∴,,
又,
∴,
∴;
(2)连接,过F作于N,
则四边形是矩形,
∴,,
又,
∴,
∵翻折,
∴,
∵,,
∴,,
又,
∴,
∴,
又,
∴,
∴,
∵,
∴,
∴,
又,,
∴,
∴,
又,,
∴
(1)①1400;164;②
(2)证明:∵四边形和四边形都是平行四边形,
∴,,,,∴,,∴四边形是平行四边形;
(3)证明:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
设,则,
∵,
∴,
∵,
∴,
∴,
∴,
∴平行四边形是菱形.
(1)3;
(2)解:四边形是菱形,理由如下;
由折叠的性质可知,,,
又∵,
∴是等腰三角形,,
∴,
∴四边形是菱形;
(3)解:如图,连接,作于,则四边形是矩形,
∴,
由题意知,是线段的中点,,
∵矩形,
∴,
∴,,
∵,,,
∴,
∴,
∴,
由折叠的性质可知,,
∴,
∴,
设,则,,,
∵,
∴,
由勾股定理得,,即,
解得,或(舍去),
∴,
∴的长为.
八年级数学
一、选择题(每小题3分、共30分)
1. 下列曲线中,表示y是x的函数的是 ( )
A. B.
C. D.
2. 司机王师傅在加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B. 数量 C. 单价 D. 金额和数量
3. 下列二次根式中,为最简二次根式的是( )
A. B. C. D.
4. 已知在中,且,,则( )
A. 5 B. C. 5或 D. 或
5. 下列各组数中,能作为直角三角形三边长的是( )
A. 4,5,6 B. 5,8,13 C. 1,1, D. 1,,4
6. 下列计算正确的是( )
A. B.
C. D.
7. 在平行四边形中,如果,那么等于( )
A. B. C. D.
8. 如图,在中,平分,交边于,,,则的长为( )
A. B. C. D.
9. 如图,已知菱形的周长为40,对角线交于点O,且,则该菱形的面积等于( )
A. 24 B. 56 C. 96 D. 48
10. 如图,在正方形中,点是的中点,点是的中点,与相交于点,设.得到以下结论:①;②;③;④.则上述结论正确的是( )
A. ①②④ B. ②③④ C. ①②③ D. ①②③④
二、填空题(每小题3分、共18分)
11. 要使式子有意义,则a的取值范围为_____
12. 点在正比例函数图象上,则y随着x的增大而 _____.
13. 如图,在等边三角形ABC中,点E、F分别是AB、AC的中点,EF=4,△ABC的周长为____.
14. 在的方格中,小正方形的边长是1,点A、B、C都在格点上,则边上的高为________.
15. 如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作分别交AB,BC于E,F两点,,则EF的长为__________.
16. 如图,在矩形中,E为对角线上与不重合的一个动点,过点E作与点F,于点G,连接,若,则的最小值_______.
三、解答题(每小题6分、共18分)
17. 计算:
(1).
(2).
18. 已知正比例函数的图象过点.
(1)写出这个正比例函数的函数解析式;
(2)已知点在这个正比例函数的图象上,求a的值.
19. 如图,在ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)若∠FDB=30°,∠ABC=45°,BC=,求DF的长.
四、解答题(每小题9分、共27分)
20. 如图1,是我国汉代的赵爽用来证明“勾股定理”的“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为、,斜边长为.
(1)图中阴影部分小正方形的面积用两种方法可分别表示为________和________;
(2)若,大正方形的边长,则小正方形的边长为________;
[知识迁移]通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是棱长为的正方体,被如图所示的分割线分成8块.
(3)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为________;
(4)已知,,利用上面的规律求的值.
21. 问题情境:通过对《平行四边形》一章内容的学习,我们认识到矩形、菱形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,还有各自的特殊性质.根据它们的特殊性,得到了这些特殊的平行四边形的判定定理.数学课上,老师给出了一道题:如图①,矩形的对角线,交于点O,过点D作,且,连接.
初步探究:
(1)判断四边形的形状,并说明理由.
深入探究:
(2)如图②,若四边形是菱形,(1)中的结论还成立吗?请说明理由.
拓展延伸:
(3)如图③,若四边形是正方形,四边形又是什么特殊的四边形?请说明理由.
22. 【阅读材料】
在学习正方形时,我们遇到过这样的问题:如图1,在正方形中,点E、F、G、H分别在、、、上,且,垂足为M,那么与相等吗?
分别过点G、H作、,垂足分别为P、Q,通过证明,得到.
根据阅读材料,完成下面探究1、探究2中的问题.
【探究1】
如图2,在正方形中,点E在上,使用无刻度的直尺和圆规作,交于点F(要求直尺、圆规各使用一次),保留作图痕迹,并标出点F,不要求写作法;
【探究2】
如图3,在正方形中,点E、F分别在、上,将正方形沿着翻折,点B、C分别落在、处,且经过点D,将纸片展开,延长交于点G,连接交于点M.
(1)求证:;
(2)求证:.
五、解答题(23题13分、24题14分,共27分)
23. 阅读材料:
中国-西班牙联合发行《中欧班列(义乌-马德里)》特种邮票1套2枚,两枚邮票的大小、形状相同(如图1).邮票在设计时采用了多种数学元素:根据画面内容邮票以平行四边形的形式呈现,代表着列车前进的速度,凸显中欧班列的动态美;中国与西班牙两个列车图形保持对称,并向外延展,凸显中欧班列的和谐美;
在单枚邮票票面上的平行四边形中,邻边与的长度比非常接近黄金分割数.单枚邮票的规格(平行四边形:长边50毫米,短边32毫米,高28毫米)见图2所示.设图1的中边上的高为.
根据以上信息解决问题:
(1)【相关计算】①单枚邮票的面积为:________,周长为:________.
②计算的长为:________(结果用最简二次根式表示);
(2)【特例证明】图1中,求证:四边形是平行四边形.
(3)【数形结合】现在将图1中的设计成标准的黄金平行四边形,也就是满足相邻两边的比为黄金分割数的平行四边形.如图3所示,即在中,两邻边、满足,现又在上取点,且满足,过点作交边于点.求证:四边形是菱形.
24. 综合与实践
数学课上,老师以“矩形的折叠”为主题开展活动.
实践操作:
现有一张矩形纸片.
第一步:如图1,将矩形纸片先沿对角线折叠,得到折痕,然后把纸片展平;
第二步:如图2,将矩形纸片折叠,使点与点重合,得到折痕,然后把纸片展平,与的交点为点,连接.
第三步:如图3,将矩形纸片沿过点的直线折叠,点的对应点为点,点的对应点为点与交于点,然后把纸片展平.
问题解决:
(1)的长为 ;
(2)判断四边形的形状,并说明理由;
拓展探索:
(3)若,求的长.
参考答案
1-10:DCDBC CACCD
减小
24、
17、(1)解:
;
(2)解:
.
18、(1)将代入正比例函数,得
正比例函数的函数解析式为;
(2)由(1)可知,
点在这个正比例函数的图象上,
19、(1)证明:∵CF∥AB,
∴∠ECF=∠EBD.
∵E是BC中点,
∴CE=BE.
∵∠CEF=∠BED,
∴△CEF≌△BED.
∴CF=BD.
∴四边形CDBF是平行四边形.
(2)解:如图,作EM⊥DB于点M,
∵四边形CDBF是平行四边形,BC=,
∴,DF=2DE.
在Rt△EMB中,EM=BE sin∠ABC=2,
在Rt△EMD中,∵∠EDM=30°,
∴DE=2EM=4,
∴DF=2DE=8.
(1);;
(2)3;
;
(4)∵,,,
∴,
∴.
21、解:(1)四边形是菱形
理由如下:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,,,
∴,
所以四边形是菱形 ;
(2)(1)中的结论不成立;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是菱形,
∴,
∴,
∴四边形是矩形
(3)四边形是正方形;
理由如下:
同(1),得四边形是平行四边形,
∵四边形是正方形,
∴,,,,
∴,,
∴四边形是正方形.
22、解∶[探究1]
如图,即为所求,
∵四边形是正方形,
∴,,,
由作图知:,
∴,
∴,
∵,
∴,
∴;
[探究2]
(1)证明:∵翻折,
∴,,
又,
∴,
∴;
(2)连接,过F作于N,
则四边形是矩形,
∴,,
又,
∴,
∵翻折,
∴,
∵,,
∴,,
又,
∴,
∴,
又,
∴,
∴,
∵,
∴,
∴,
又,,
∴,
∴,
又,,
∴
(1)①1400;164;②
(2)证明:∵四边形和四边形都是平行四边形,
∴,,,,∴,,∴四边形是平行四边形;
(3)证明:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
设,则,
∵,
∴,
∵,
∴,
∴,
∴,
∴平行四边形是菱形.
(1)3;
(2)解:四边形是菱形,理由如下;
由折叠的性质可知,,,
又∵,
∴是等腰三角形,,
∴,
∴四边形是菱形;
(3)解:如图,连接,作于,则四边形是矩形,
∴,
由题意知,是线段的中点,,
∵矩形,
∴,
∴,,
∵,,,
∴,
∴,
∴,
由折叠的性质可知,,
∴,
∴,
设,则,,,
∵,
∴,
由勾股定理得,,即,
解得,或(舍去),
∴,
∴的长为.
同课章节目录
