2.2探索直线平行的条件(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 2.2探索直线平行的条件(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 16:37:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
探索直线平行的条件
一.选择题(共10小题)
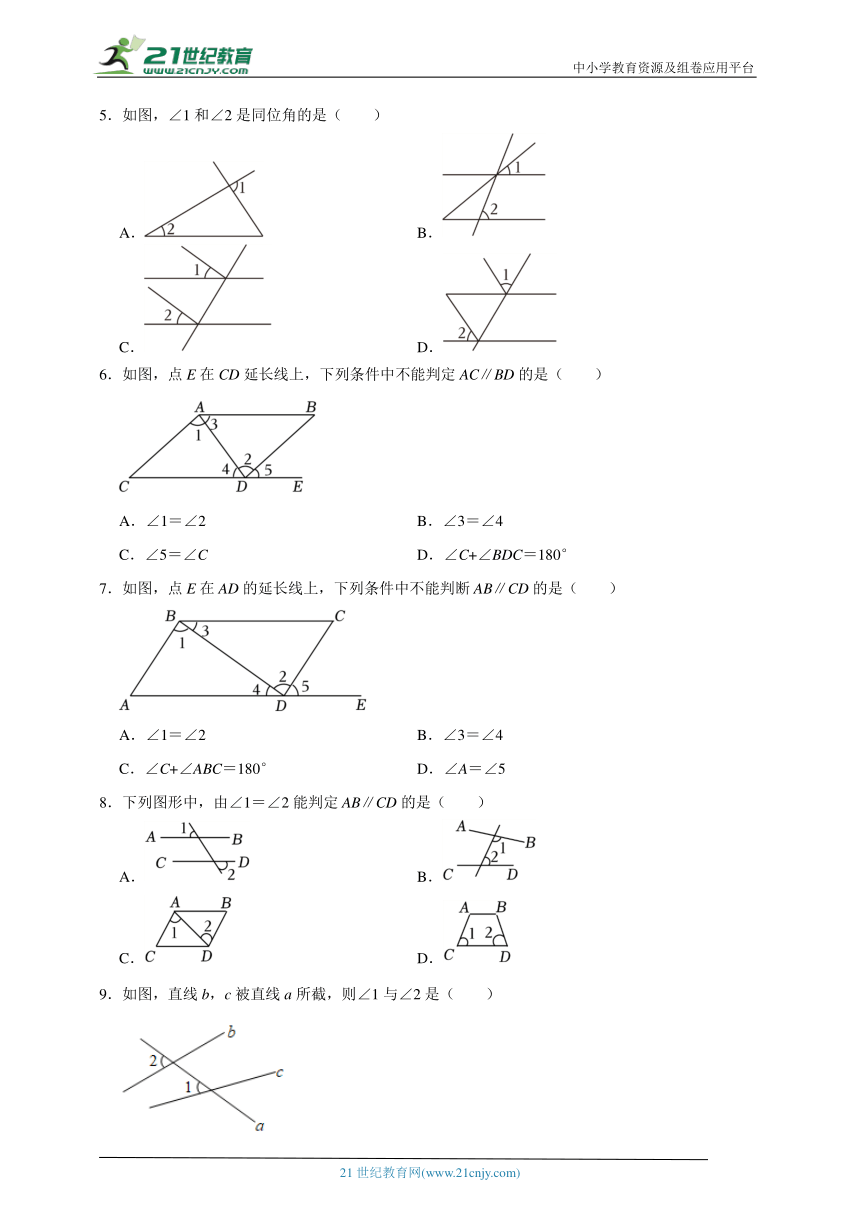
1.如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是( )
A.∠2=∠4 B.∠B=∠5
C.∠5=∠D D.∠D+∠DAB=180°
2.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D.∠D+∠DCA=180°
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是( )
A.①② B.①③ C.②③ D.②④
4.如图是小明探索直线平行的条件时所用的学具,木条a,b,c在同一平面内.经测量∠1=70°,要使木条a∥b,则∠2的度数应为( )
A.20° B.70° C.110° D.160°
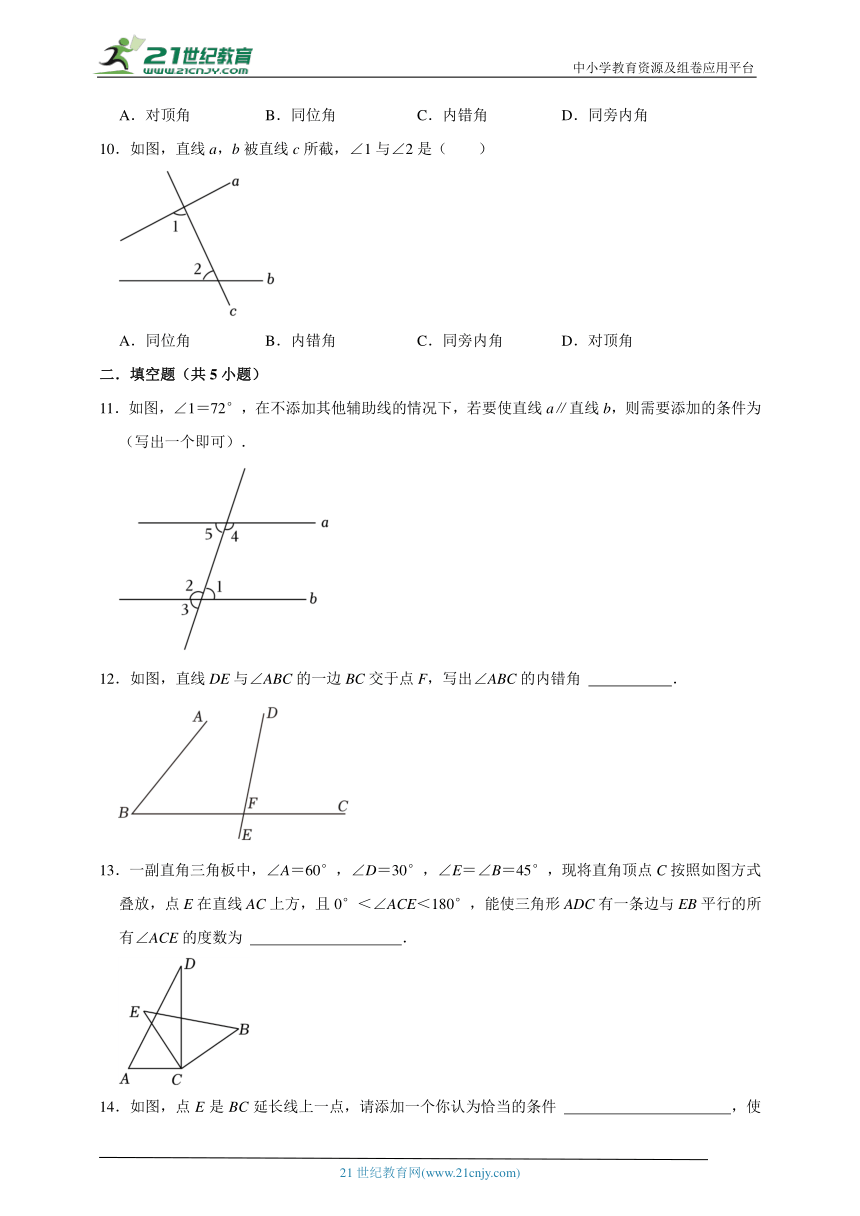
5.如图,∠1和∠2是同位角的是( )
A. B.
C. D.
6.如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠5=∠C D.∠C+∠BDC=180°
7.如图,点E在AD的延长线上,下列条件中不能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠C+∠ABC=180° D.∠A=∠5
8.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B.
C. D.
9.如图,直线b,c被直线a所截,则∠1与∠2是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
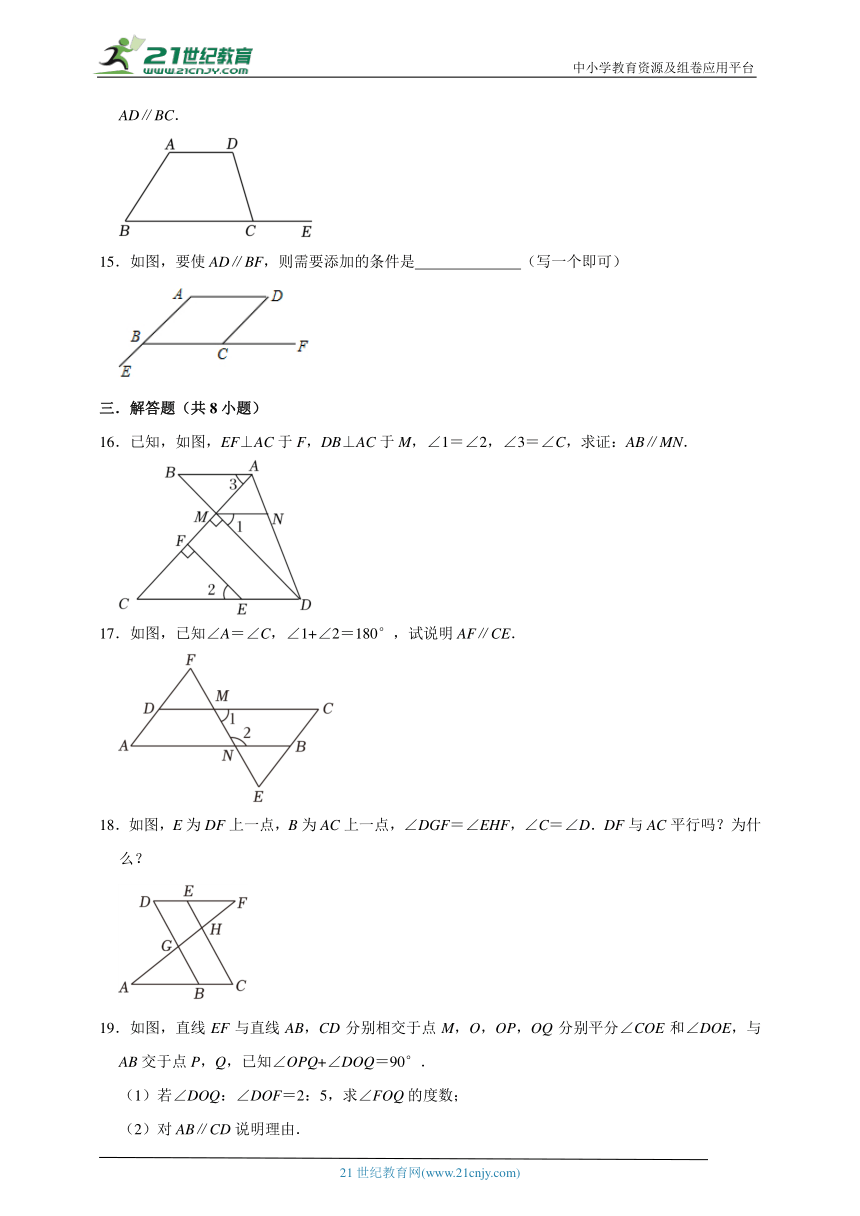
10.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
二.填空题(共5小题)
11.如图,∠1=72°,在不添加其他辅助线的情况下,若要使直线a∥直线b,则需要添加的条件为 (写出一个即可).
12.如图,直线DE与∠ABC的一边BC交于点F,写出∠ABC的内错角 .
13.一副直角三角板中,∠A=60°,∠D=30°,∠E=∠B=45°,现将直角顶点C按照如图方式叠放,点E在直线AC上方,且0°<∠ACE<180°,能使三角形ADC有一条边与EB平行的所有∠ACE的度数为 .
14.如图,点E是BC延长线上一点,请添加一个你认为恰当的条件 ,使AD∥BC.
15.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
三.解答题(共8小题)
16.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
17.如图,已知∠A=∠C,∠1+∠2=180°,试说明AF∥CE.
18.如图,E为DF上一点,B为AC上一点,∠DGF=∠EHF,∠C=∠D.DF与AC平行吗?为什么?
19.如图,直线EF与直线AB,CD分别相交于点M,O,OP,OQ分别平分∠COE和∠DOE,与AB交于点P,Q,已知∠OPQ+∠DOQ=90°.
(1)若∠DOQ:∠DOF=2:5,求∠FOQ的度数;
(2)对AB∥CD说明理由.
20.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.
(1)求∠CFD的度数;
(2)请判断AB与CD是否平行,说明理由.
21.如图,点O为直线AB上一点,OF⊥OE,∠DOE=55°,OF平分∠AOD,∠D=110°.证明:CD∥AB.
22.如图,已知∠BAF=∠AFD,∠ABC+∠CDE=180°,求证:BC∥DE.
23.如图1,AC平分∠DAB,∠1=∠2.
(1)试说明AB与CD的位置关系,并予以证明;
(2)如图2,当∠ADC=120°时,点E、F分别在CD和AC的延长线上运动,试探讨∠E和∠F的数量关系;
(3)如图3,AD和BC交于点G,过点D作DH∥BC交AC于点H,若AC⊥BC,问当∠CDH为多少度时,∠GDC=∠ADH.
探索直线平行的条件
参考答案与试题解析
一.选择题(共10小题)
1.【答案】C
【分析】根据平行线的判定定理“同位角相等,两直线平行”、“内错角相等,两直线平行”、“同旁内角互补,两直线平行”分别进行分析.
【解答】解:A、根据内错角相等,两直线平行可判定AB∥CD,故此选项不合题意;
B、根据同位角相等,两直线平行可判定AB∥CD,故此选项不合题意;
C、根据内错角相等,两直线平行可判定AD∥CB,无法判定AB∥CD,故此选项符合题意;
D、根据同旁内角互补,两直线平行可判定AB∥CD,故此选项不合题意;
故选:C.
【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
2.【答案】B
【分析】根据平行线的判定分别进行分析可得答案.
【解答】解:A、∠3=∠4,根据内错角相等,BD∥AC,故此选项不符合题意;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项符合题意;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项不符合题意;
D、∠D+∠DCA=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项不符合题意.
故选:B.
【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
3.【答案】B
【分析】利用平行线的判定方法判断即可得到正确的选项.
【解答】解:①∵∠1=∠2,
∴AB∥DC,本选项符合题意;
②∵∠3=∠4,
∴AD∥CB,本选项不符合题意;
③∵∠B=∠DCE,
∴AB∥CD,本选项符合题意;
④∵∠B+∠BAD=180°,
∴AD∥CB,本选项不符合题意.
则符合题意的选项为①③.
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
4.【答案】C
【分析】根据邻补角互补和平行线的判定定理求解即可.
【解答】解:∠2的度数应为110°.
证明:如图,
∵∠2=110°,
∴∠3=180°﹣110°=70°,
∴∠1=∠3,
∴a∥b.
故选:C.
【点评】本题考查邻补角互补,平行线的判定.熟练掌握平行线的判定定理是解题关键.
5.【答案】A
【分析】根据同位角的定义判断求解.
【解答】解:A:∠1和∠2是同位角,故A是正确的;
B、C、D中的∠1和∠2的边都是四条直线,不是“三线八角”,故B、C、D都是错误的;
故选:A.
【点评】本题考查了同位角、内错角,同旁内角的定义,正确识别各种角的关系是解题的关键.
6.【答案】B
【分析】根据平行线的判定方法直接判定即可.
【解答】解:A.∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,所以A选项不符合题意.
B.∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意.
C.∵∠5=∠C,∴BD∥AC (同位角相等,两直线平行),所以C选项不合题意.
D.∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D选项不合题意.
故选:B.
【点评】本题主要考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
7.【答案】B
【分析】根据平行线的判定方法,逐一进行判定即可.
【解答】解:A、∵∠1=∠2,
∴AB∥CD,故本选项不符合题意;
B、∵∠3=∠4,
∴AD∥BC,故本选项符合题意;
C、∵∠C+∠ABC=180°,
∴AB∥CD,故本选项不符合题意;
D、∵∠A=∠5,
∴AB∥CD,故本选项不符合题意;
故选:B.
【点评】本题主要考查平行线的判定,掌握平行线的判定方法是解题的关键.
8.【答案】A
【分析】根据平行线的判定定理判断求解即可.
【解答】解:A、如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴AB∥CD,
故A符合题意;
B、由∠1=∠2不能判定AB∥CD,
故B不符合题意;
C、∵∠1=∠2,
∴AC∥BD,
故C不符合题意;
D、由∠1=∠2不能判定AB∥CD,
故D不符合题意;
故选:A.
【点评】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
9.【答案】B
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【解答】解:由题意可得,∠1与∠2是直线b,c被直线a所截而成的同位角.
故选:B.
【点评】本题主要考查了同位角,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
10.【答案】C
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解答】解:直线a,b被直线c所截,∠1与∠2是同旁内角.
故选:C.
【点评】本题考查同旁内角,关键是掌握同旁内角的定义.
二.填空题(共5小题)
11.【答案】∠5=72°(答案不唯一),
【分析】由平行线的判定,即可得到答案.
【解答】解:要使直线a∥直线b,则需要添加的条件为∠5=72°(答案不唯一),理由如下:
∵∠1=72°,2=72°,
∴∠1=∠2,
∴a∥b.
故答案为:∠5=72°(答案不唯一).
【点评】本题考查平行线的判定,关键是掌握平行线的判定方法.
12.【答案】∠BFE.
【分析】根据内错角的定义:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫作内错角,即可得解.
【解答】解:∠ABC的内错角是∠BFE,
故答案为:∠BFE.
【点评】本题考查了内错角,熟记内错角的概念是解题关键.
13.【答案】45°或135°或165°.
【分析】旋转三角形ADC,使其三边分别与BE形成平行状态,根据平行线的判定定理分情况讨论求解即可.
【解答】解:当∠ACE=∠E=45°时,AC∥BE,理由如下,如图所示:
∵∠ACE=∠DCB=45°,∠B=45°,
∴BE⊥CD.
又∵AC⊥CD,
∴AC∥BE;
当∠ACE=135°时,BE∥CD,理由如下,如图所示:
∵∠ACE=135°,
∴∠DCE=135°﹣90°=45°,
∵∠E=45°,
∴∠DCE=∠E,
∴BE∥CD;
当∠ACE=165°时,BE∥AD.理由如下:
延长AC交BE于F,如图所示:
∵∠ACE=165°,
∴∠ECF=15°,
∵∠E=45°,
∴∠CFB=∠ECF+∠E=60°,
∵∠A=60°,
∴∠A=∠CFB,
∴BE∥AD,
综上,三角形ADC有一条边与EB平行的所有∠ACE的度数的为:45°或135°或165°.
故答案为:45°或135°或165°.
【点评】此题考查了平行线的判定,三角形外角定理,熟记平行线的判定定理是解题的关键.
14.【答案】∠A+∠B=180°(不唯一).
【分析】根据同旁内角互补两直线平行来解答即可,答案不唯一.
【解答】解:∵∠A+∠B=180°,
∴AD∥BC.
故答案为:∠A+∠B=180°(不唯一).
【点评】本题考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键.
15.【答案】见试题解答内容
【分析】依据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,即可得到添加的条件.
【解答】解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
【点评】本题主要考查了平行线的判定,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
三.解答题(共8小题)
16.【答案】见试题解答内容
【分析】由于EF⊥AC,DB⊥AC得到EF∥DM,根据平行线的性质得∠2=∠CDM,而∠1=∠2,则∠1=∠CDM,根据平行线的判定得到MN∥CD,所以∠C=∠AMN,又∠3=∠C,于是∠3=∠AMN,然后根据平行线的判定即可得到AB∥MN.
【解答】证明:∵EF⊥AC,DB⊥AC,
∴EF∥DM,
∴∠2=∠CDM,
∵∠1=∠2,
∴∠1=∠CDM,
∴MN∥CD,
∴∠C=∠AMN,
∵∠3=∠C,
∴∠3=∠AMN,
∴AB∥MN.
【点评】本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.
17.【答案】见解答过程.
【分析】由同旁内角互补,两直线平行可得CD∥AB,则有∠A=∠CDF,从而可求得∠C=∠CDF,即可判定AF∥CE.
【解答】解:∵∠1+∠2=180°,
∴CD∥AB,
∴∠A=∠CDF,
∵∠A=∠C,
∴∠C=∠CDF,
∴AF∥CE.
【点评】本题主要考查平行线的判定,解答的关键是熟记平行线的判定定理并灵活运用.
18.【答案】DF与AC平行,理由见解析.
【分析】由∠DGF=∠EHF,推出BD∥EC,得到∠ABG=∠C,有∠D=∠C,得到∠D=∠ABG,因此 DF∥AC.
【解答】解:DF与AC平行,理由如下,
∵∠DGF=∠EHF,
∴BD∥EC,
∴∠ABG=∠C,
∵∠D=∠C,
∴∠D=∠ABG,
∴DF∥AC.
【点评】本题考查平行线的判定,关键是由BD∥EC推出∠D=∠ABG,即可判定FD与AC平行.
19.【答案】(1)140°;(2)理由见解析.
【分析】(1)由OQ分别平分∠DOE,得到∠EOQ=∠DOQ,又∠DOQ:∠DOF=2:5,推出∠EOQ180°=40°,即可求出∠FOQ=180°﹣∠EOQ=140°;
(2)由角平分线定义推出∠POQ∠COD180°=90°,得到∠PQO+∠OPQ=90°,又∠OPQ+∠DOQ=90°,得到∠PQO=∠DOQ,推出AB∥CD.
【解答】解:(1)∵OQ分别平分∠DOE,
∴∠EOQ=∠DOQ,
∵∠DOQ:∠DOF=2:5,
∴∠EOQ:∠DOQ:∠DOF=2:2:5,
∵∠EOQ+∠DOQ+∠DOF=180°,
∴∠EOQ180°=40°,
∴∠FOQ=180°﹣∠EOQ=140°;
(2)∵OP,OQ分别平分∠COE和∠DOE,
∴∠POM∠COM,∠QOM∠DOM,
∴∠POM+∠QOM(∠COM+∠DOM),
∴∠POQ∠COD180°=90°,
∴∠PQO+∠OPQ=90°,
∵∠OPQ+∠DOQ=90°,
∴∠PQO=∠DOQ,
∴AB∥CD.
【点评】本题考查平行线的判定,角平分线定义,关键是掌握平行线的判定方法;由角平分线定义,推出∠POQ∠COD180°=90°.
20.【答案】(1)90°;
(2)AB∥CD,理由见详解.
【分析】(1)先由∠C=∠1得CF∥EB,再因为BE⊥FD得∠DGE=90°,即可求∠CFD的度数;
(2)由(1)知∠DGE=90°,则∠1+∠D=90°,再因为∠2和∠D互余,即得∠1=∠2,由∠C=∠1得∠C=∠2即可得解.
【解答】解:(1)∵∠C=∠1,
∴CF∥EB,
∵BE⊥FD,
∴∠DGE=90°,
∵CF∥EB,
∴∠CFD=∠DGE=90°;
(2)AB∥CD,理由如下:
由(1)知∠DGE=90°,
则∠1+∠D=90°,
∵∠2和∠D互余,
∴∠2+∠D=90°,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
【点评】本题主要考查的是平行线的性质与判定等知识内容,正确掌握平行线的性质与判定是解题的关键.
21.【答案】证明见解析.
【分析】利用角平分线的定义与垂直的定义求出∠AOD=70°,从而得出∠AOD+∠D=180°,即可由平行线的判定定理得出结论.
【解答】证明:∵OF⊥OE,
∴∠FOE=90°,
∵∠DOE=55°,
∴∠DOF=35°,
∵OF平分∠AOD,
∴∠AOD=2∠DOF=2×35°=70°,
∴∠AOD+∠D=70°+110°=180°,
∴CD∥AB.
【点评】本题考查了平行线的判定定理,角平分线与垂直的定义,熟练掌握平行线的判定定理是解题的关键.
22.【答案】证明见解答过程.
【分析】根据平行线的判定与性质求解即可.
【解答】证明:∵∠BAF=∠AFD,
∴AB∥CD,
∴∠ABC+∠C=180°,
∵∠ABC+∠CDE=180°,
∴∠C=∠CDE,
∴BC∥DE.
【点评】此题考查了平行线的判定.熟记“内错角相等,两直线平行”是解题的关键.
23.【答案】见试题解答内容
【分析】(1)依据AC平分∠DAB,∠1=∠2,即可得到∠2=∠BAC,进而判定CD∥AB.
(2)当∠ADC=120°时,∠1=∠2=30°,依据∠2是△CEF的外角,可得∠E+∠F=∠2=30°.
(3)依据DH∥BC,AC⊥BC,可得DH⊥AC,进而得到∠ADH=∠CDH,据此可得当∠GDC=∠ADH时,∠CDG=∠CDH=∠ADH,即可得到∠CDH180°=60°.
【解答】解:(1)如图,∵AC平分∠DAB,
∴∠1=∠BAC,
又∵∠1=∠2,
∴∠2=∠BAC,
∴CD∥AB.
(2)当∠ADC=120°时,∠1=∠2=30°,
∵点E、F分别在CD和AC的延长线上运动,
∴∠2是△CEF的外角,
∴∠E+∠F=∠2=30°.
(3)∵DH∥BC,AC⊥BC,
∴DH⊥AC,
又∵∠1=∠2,
∴∠ADH=∠CDH,
∴当∠GDC=∠ADH时,∠CDG=∠CDH=∠ADH,
∴∠CDH180°=60°.
故当∠CDH为60度时,∠GDC=∠ADH.
【点评】本题主要考查了平行线的判定以及三角形外角性质的运用,两条直线被第三条所截,如果内错角相等,那么这两条直线平行.即内错角相等,两直线平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
探索直线平行的条件
一.选择题(共10小题)
1.如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是( )
A.∠2=∠4 B.∠B=∠5
C.∠5=∠D D.∠D+∠DAB=180°
2.如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D.∠D+∠DCA=180°
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是( )
A.①② B.①③ C.②③ D.②④
4.如图是小明探索直线平行的条件时所用的学具,木条a,b,c在同一平面内.经测量∠1=70°,要使木条a∥b,则∠2的度数应为( )
A.20° B.70° C.110° D.160°
5.如图,∠1和∠2是同位角的是( )
A. B.
C. D.
6.如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠5=∠C D.∠C+∠BDC=180°
7.如图,点E在AD的延长线上,下列条件中不能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠C+∠ABC=180° D.∠A=∠5
8.下列图形中,由∠1=∠2能判定AB∥CD的是( )
A. B.
C. D.
9.如图,直线b,c被直线a所截,则∠1与∠2是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
10.如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
二.填空题(共5小题)
11.如图,∠1=72°,在不添加其他辅助线的情况下,若要使直线a∥直线b,则需要添加的条件为 (写出一个即可).
12.如图,直线DE与∠ABC的一边BC交于点F,写出∠ABC的内错角 .
13.一副直角三角板中,∠A=60°,∠D=30°,∠E=∠B=45°,现将直角顶点C按照如图方式叠放,点E在直线AC上方,且0°<∠ACE<180°,能使三角形ADC有一条边与EB平行的所有∠ACE的度数为 .
14.如图,点E是BC延长线上一点,请添加一个你认为恰当的条件 ,使AD∥BC.
15.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
三.解答题(共8小题)
16.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
17.如图,已知∠A=∠C,∠1+∠2=180°,试说明AF∥CE.
18.如图,E为DF上一点,B为AC上一点,∠DGF=∠EHF,∠C=∠D.DF与AC平行吗?为什么?
19.如图,直线EF与直线AB,CD分别相交于点M,O,OP,OQ分别平分∠COE和∠DOE,与AB交于点P,Q,已知∠OPQ+∠DOQ=90°.
(1)若∠DOQ:∠DOF=2:5,求∠FOQ的度数;
(2)对AB∥CD说明理由.
20.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.
(1)求∠CFD的度数;
(2)请判断AB与CD是否平行,说明理由.
21.如图,点O为直线AB上一点,OF⊥OE,∠DOE=55°,OF平分∠AOD,∠D=110°.证明:CD∥AB.
22.如图,已知∠BAF=∠AFD,∠ABC+∠CDE=180°,求证:BC∥DE.
23.如图1,AC平分∠DAB,∠1=∠2.
(1)试说明AB与CD的位置关系,并予以证明;
(2)如图2,当∠ADC=120°时,点E、F分别在CD和AC的延长线上运动,试探讨∠E和∠F的数量关系;
(3)如图3,AD和BC交于点G,过点D作DH∥BC交AC于点H,若AC⊥BC,问当∠CDH为多少度时,∠GDC=∠ADH.
探索直线平行的条件
参考答案与试题解析
一.选择题(共10小题)
1.【答案】C
【分析】根据平行线的判定定理“同位角相等,两直线平行”、“内错角相等,两直线平行”、“同旁内角互补,两直线平行”分别进行分析.
【解答】解:A、根据内错角相等,两直线平行可判定AB∥CD,故此选项不合题意;
B、根据同位角相等,两直线平行可判定AB∥CD,故此选项不合题意;
C、根据内错角相等,两直线平行可判定AD∥CB,无法判定AB∥CD,故此选项符合题意;
D、根据同旁内角互补,两直线平行可判定AB∥CD,故此选项不合题意;
故选:C.
【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
2.【答案】B
【分析】根据平行线的判定分别进行分析可得答案.
【解答】解:A、∠3=∠4,根据内错角相等,BD∥AC,故此选项不符合题意;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项符合题意;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项不符合题意;
D、∠D+∠DCA=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项不符合题意.
故选:B.
【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
3.【答案】B
【分析】利用平行线的判定方法判断即可得到正确的选项.
【解答】解:①∵∠1=∠2,
∴AB∥DC,本选项符合题意;
②∵∠3=∠4,
∴AD∥CB,本选项不符合题意;
③∵∠B=∠DCE,
∴AB∥CD,本选项符合题意;
④∵∠B+∠BAD=180°,
∴AD∥CB,本选项不符合题意.
则符合题意的选项为①③.
故选:B.
【点评】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
4.【答案】C
【分析】根据邻补角互补和平行线的判定定理求解即可.
【解答】解:∠2的度数应为110°.
证明:如图,
∵∠2=110°,
∴∠3=180°﹣110°=70°,
∴∠1=∠3,
∴a∥b.
故选:C.
【点评】本题考查邻补角互补,平行线的判定.熟练掌握平行线的判定定理是解题关键.
5.【答案】A
【分析】根据同位角的定义判断求解.
【解答】解:A:∠1和∠2是同位角,故A是正确的;
B、C、D中的∠1和∠2的边都是四条直线,不是“三线八角”,故B、C、D都是错误的;
故选:A.
【点评】本题考查了同位角、内错角,同旁内角的定义,正确识别各种角的关系是解题的关键.
6.【答案】B
【分析】根据平行线的判定方法直接判定即可.
【解答】解:A.∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,所以A选项不符合题意.
B.∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意.
C.∵∠5=∠C,∴BD∥AC (同位角相等,两直线平行),所以C选项不合题意.
D.∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D选项不合题意.
故选:B.
【点评】本题主要考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
7.【答案】B
【分析】根据平行线的判定方法,逐一进行判定即可.
【解答】解:A、∵∠1=∠2,
∴AB∥CD,故本选项不符合题意;
B、∵∠3=∠4,
∴AD∥BC,故本选项符合题意;
C、∵∠C+∠ABC=180°,
∴AB∥CD,故本选项不符合题意;
D、∵∠A=∠5,
∴AB∥CD,故本选项不符合题意;
故选:B.
【点评】本题主要考查平行线的判定,掌握平行线的判定方法是解题的关键.
8.【答案】A
【分析】根据平行线的判定定理判断求解即可.
【解答】解:A、如图,
∵∠1=∠2,∠3=∠2,
∴∠1=∠3,
∴AB∥CD,
故A符合题意;
B、由∠1=∠2不能判定AB∥CD,
故B不符合题意;
C、∵∠1=∠2,
∴AC∥BD,
故C不符合题意;
D、由∠1=∠2不能判定AB∥CD,
故D不符合题意;
故选:A.
【点评】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
9.【答案】B
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【解答】解:由题意可得,∠1与∠2是直线b,c被直线a所截而成的同位角.
故选:B.
【点评】本题主要考查了同位角,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
10.【答案】C
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解答】解:直线a,b被直线c所截,∠1与∠2是同旁内角.
故选:C.
【点评】本题考查同旁内角,关键是掌握同旁内角的定义.
二.填空题(共5小题)
11.【答案】∠5=72°(答案不唯一),
【分析】由平行线的判定,即可得到答案.
【解答】解:要使直线a∥直线b,则需要添加的条件为∠5=72°(答案不唯一),理由如下:
∵∠1=72°,2=72°,
∴∠1=∠2,
∴a∥b.
故答案为:∠5=72°(答案不唯一).
【点评】本题考查平行线的判定,关键是掌握平行线的判定方法.
12.【答案】∠BFE.
【分析】根据内错角的定义:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫作内错角,即可得解.
【解答】解:∠ABC的内错角是∠BFE,
故答案为:∠BFE.
【点评】本题考查了内错角,熟记内错角的概念是解题关键.
13.【答案】45°或135°或165°.
【分析】旋转三角形ADC,使其三边分别与BE形成平行状态,根据平行线的判定定理分情况讨论求解即可.
【解答】解:当∠ACE=∠E=45°时,AC∥BE,理由如下,如图所示:
∵∠ACE=∠DCB=45°,∠B=45°,
∴BE⊥CD.
又∵AC⊥CD,
∴AC∥BE;
当∠ACE=135°时,BE∥CD,理由如下,如图所示:
∵∠ACE=135°,
∴∠DCE=135°﹣90°=45°,
∵∠E=45°,
∴∠DCE=∠E,
∴BE∥CD;
当∠ACE=165°时,BE∥AD.理由如下:
延长AC交BE于F,如图所示:
∵∠ACE=165°,
∴∠ECF=15°,
∵∠E=45°,
∴∠CFB=∠ECF+∠E=60°,
∵∠A=60°,
∴∠A=∠CFB,
∴BE∥AD,
综上,三角形ADC有一条边与EB平行的所有∠ACE的度数的为:45°或135°或165°.
故答案为:45°或135°或165°.
【点评】此题考查了平行线的判定,三角形外角定理,熟记平行线的判定定理是解题的关键.
14.【答案】∠A+∠B=180°(不唯一).
【分析】根据同旁内角互补两直线平行来解答即可,答案不唯一.
【解答】解:∵∠A+∠B=180°,
∴AD∥BC.
故答案为:∠A+∠B=180°(不唯一).
【点评】本题考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键.
15.【答案】见试题解答内容
【分析】依据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,即可得到添加的条件.
【解答】解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
【点评】本题主要考查了平行线的判定,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
三.解答题(共8小题)
16.【答案】见试题解答内容
【分析】由于EF⊥AC,DB⊥AC得到EF∥DM,根据平行线的性质得∠2=∠CDM,而∠1=∠2,则∠1=∠CDM,根据平行线的判定得到MN∥CD,所以∠C=∠AMN,又∠3=∠C,于是∠3=∠AMN,然后根据平行线的判定即可得到AB∥MN.
【解答】证明:∵EF⊥AC,DB⊥AC,
∴EF∥DM,
∴∠2=∠CDM,
∵∠1=∠2,
∴∠1=∠CDM,
∴MN∥CD,
∴∠C=∠AMN,
∵∠3=∠C,
∴∠3=∠AMN,
∴AB∥MN.
【点评】本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.
17.【答案】见解答过程.
【分析】由同旁内角互补,两直线平行可得CD∥AB,则有∠A=∠CDF,从而可求得∠C=∠CDF,即可判定AF∥CE.
【解答】解:∵∠1+∠2=180°,
∴CD∥AB,
∴∠A=∠CDF,
∵∠A=∠C,
∴∠C=∠CDF,
∴AF∥CE.
【点评】本题主要考查平行线的判定,解答的关键是熟记平行线的判定定理并灵活运用.
18.【答案】DF与AC平行,理由见解析.
【分析】由∠DGF=∠EHF,推出BD∥EC,得到∠ABG=∠C,有∠D=∠C,得到∠D=∠ABG,因此 DF∥AC.
【解答】解:DF与AC平行,理由如下,
∵∠DGF=∠EHF,
∴BD∥EC,
∴∠ABG=∠C,
∵∠D=∠C,
∴∠D=∠ABG,
∴DF∥AC.
【点评】本题考查平行线的判定,关键是由BD∥EC推出∠D=∠ABG,即可判定FD与AC平行.
19.【答案】(1)140°;(2)理由见解析.
【分析】(1)由OQ分别平分∠DOE,得到∠EOQ=∠DOQ,又∠DOQ:∠DOF=2:5,推出∠EOQ180°=40°,即可求出∠FOQ=180°﹣∠EOQ=140°;
(2)由角平分线定义推出∠POQ∠COD180°=90°,得到∠PQO+∠OPQ=90°,又∠OPQ+∠DOQ=90°,得到∠PQO=∠DOQ,推出AB∥CD.
【解答】解:(1)∵OQ分别平分∠DOE,
∴∠EOQ=∠DOQ,
∵∠DOQ:∠DOF=2:5,
∴∠EOQ:∠DOQ:∠DOF=2:2:5,
∵∠EOQ+∠DOQ+∠DOF=180°,
∴∠EOQ180°=40°,
∴∠FOQ=180°﹣∠EOQ=140°;
(2)∵OP,OQ分别平分∠COE和∠DOE,
∴∠POM∠COM,∠QOM∠DOM,
∴∠POM+∠QOM(∠COM+∠DOM),
∴∠POQ∠COD180°=90°,
∴∠PQO+∠OPQ=90°,
∵∠OPQ+∠DOQ=90°,
∴∠PQO=∠DOQ,
∴AB∥CD.
【点评】本题考查平行线的判定,角平分线定义,关键是掌握平行线的判定方法;由角平分线定义,推出∠POQ∠COD180°=90°.
20.【答案】(1)90°;
(2)AB∥CD,理由见详解.
【分析】(1)先由∠C=∠1得CF∥EB,再因为BE⊥FD得∠DGE=90°,即可求∠CFD的度数;
(2)由(1)知∠DGE=90°,则∠1+∠D=90°,再因为∠2和∠D互余,即得∠1=∠2,由∠C=∠1得∠C=∠2即可得解.
【解答】解:(1)∵∠C=∠1,
∴CF∥EB,
∵BE⊥FD,
∴∠DGE=90°,
∵CF∥EB,
∴∠CFD=∠DGE=90°;
(2)AB∥CD,理由如下:
由(1)知∠DGE=90°,
则∠1+∠D=90°,
∵∠2和∠D互余,
∴∠2+∠D=90°,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
【点评】本题主要考查的是平行线的性质与判定等知识内容,正确掌握平行线的性质与判定是解题的关键.
21.【答案】证明见解析.
【分析】利用角平分线的定义与垂直的定义求出∠AOD=70°,从而得出∠AOD+∠D=180°,即可由平行线的判定定理得出结论.
【解答】证明:∵OF⊥OE,
∴∠FOE=90°,
∵∠DOE=55°,
∴∠DOF=35°,
∵OF平分∠AOD,
∴∠AOD=2∠DOF=2×35°=70°,
∴∠AOD+∠D=70°+110°=180°,
∴CD∥AB.
【点评】本题考查了平行线的判定定理,角平分线与垂直的定义,熟练掌握平行线的判定定理是解题的关键.
22.【答案】证明见解答过程.
【分析】根据平行线的判定与性质求解即可.
【解答】证明:∵∠BAF=∠AFD,
∴AB∥CD,
∴∠ABC+∠C=180°,
∵∠ABC+∠CDE=180°,
∴∠C=∠CDE,
∴BC∥DE.
【点评】此题考查了平行线的判定.熟记“内错角相等,两直线平行”是解题的关键.
23.【答案】见试题解答内容
【分析】(1)依据AC平分∠DAB,∠1=∠2,即可得到∠2=∠BAC,进而判定CD∥AB.
(2)当∠ADC=120°时,∠1=∠2=30°,依据∠2是△CEF的外角,可得∠E+∠F=∠2=30°.
(3)依据DH∥BC,AC⊥BC,可得DH⊥AC,进而得到∠ADH=∠CDH,据此可得当∠GDC=∠ADH时,∠CDG=∠CDH=∠ADH,即可得到∠CDH180°=60°.
【解答】解:(1)如图,∵AC平分∠DAB,
∴∠1=∠BAC,
又∵∠1=∠2,
∴∠2=∠BAC,
∴CD∥AB.
(2)当∠ADC=120°时,∠1=∠2=30°,
∵点E、F分别在CD和AC的延长线上运动,
∴∠2是△CEF的外角,
∴∠E+∠F=∠2=30°.
(3)∵DH∥BC,AC⊥BC,
∴DH⊥AC,
又∵∠1=∠2,
∴∠ADH=∠CDH,
∴当∠GDC=∠ADH时,∠CDG=∠CDH=∠ADH,
∴∠CDH180°=60°.
故当∠CDH为60度时,∠GDC=∠ADH.
【点评】本题主要考查了平行线的判定以及三角形外角性质的运用,两条直线被第三条所截,如果内错角相等,那么这两条直线平行.即内错角相等,两直线平行.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
