4.1认识三角形(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 4.1认识三角形(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 240.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 16:31:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
认识三角形
一.选择题(共10小题)
1.下列三条线段的长度,能组成三角形的是( )
A.3,3,6 B.5,6,12 C.2,5,7 D.6,7,8
2.已知三角形的两条边长分别为2和6,则第三边的长可能是( )
A.1 B.2 C.7 D.9
3.如图,为估计池塘岸边A,B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
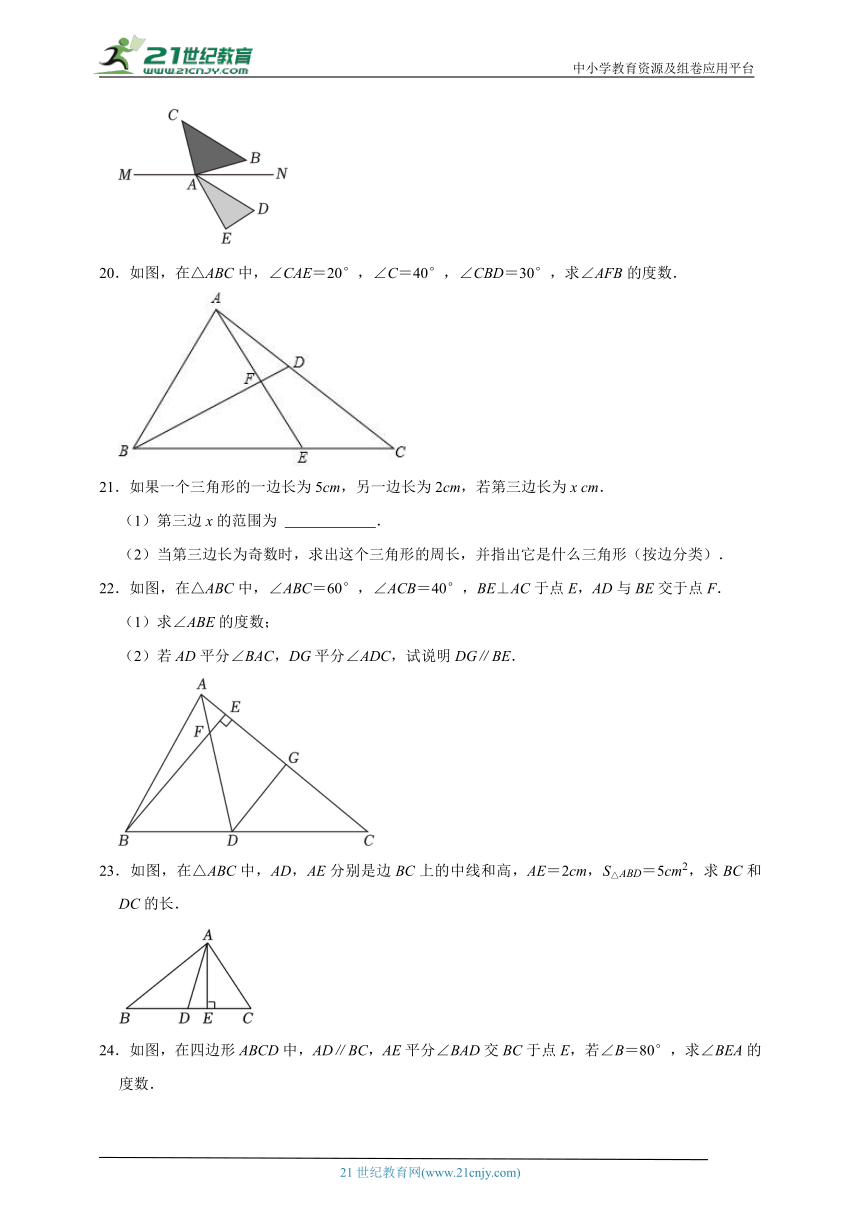
A.25米 B.15米 C.10米 D.6米
4.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
5.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
6.直角三角形两个锐角平分线相交所成的钝角的度数为( )
A.90° B.135° C.120° D.45°或135°
7.幼儿园的小朋友用木棒做拼图形游戏,一个孩子手中有2根木棒长度分别为3cm和5cm,下列木棒不能使其能围成一个三角形的是( )
A.2cm B.3cm C.4cm D.5cm
8.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
9.已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
10.下列长度的三条线段能组成三角形的是( )
A.1cm、2cm,3cm B.6cm、2cm,3cm
C.4cm、6cm,8cm D.5cm,6cm,12cm
二.填空题(共6小题)
11.如图,在△ABC中,AD是∠BAC的平分线,过点C的射线CE与AD平行,若∠B=60°,∠ACB=30°,则∠ACE= °.
12.如图,在△ABC中,已知BD是∠ABC的角平分线,点D是△ABC内一点,且AD⊥BD,∠DAC=20°,∠C=38°,那么∠BAD= °.
13.如图,BD是△ABC的中线,G是BD上的一点,且BG=2GD,连接AG,若△ABC的面积为6,则图中阴影部分的面积是 .
14.如图,点M,N分别在AB,AC上,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC= °.
15.如图,在三角形ABC中,∠ACB=90°,CD是斜边AB上的高,若AB=5,BC=4,AC=3,则高CD的长度为 .
16.如图,△ABC中AD,BE分别是△ABC的高和角平分线,若∠C=70°,∠AEB=95°,则∠BAD= °.
三.解答题(共9小题)
17.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
18.已知三角形的两边长为5和7,第三边的边长a.
(1)求a的取值范围;
(2)若a为整数,当a为何值时,组成的三角形的周长最大,最大值是多少?
19.将一副三角板的两个顶点按图所示重叠摆放在直线MN上,且三角板ADE始终摆放在直线MN下方,三角板ABC可绕点A任意旋转.已知∠CAB=∠AED=90°,∠C=45°,∠EAD=30°.设∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150).
(1)当m+n=0时,求∠CAE的度数;
(2)当n=2m(m≠0)时,求∠CAM与∠MAE的数量关系;
(3)当点C,A,E三点共线时,请通过画图探究说明m与n的数量关系.
20.如图,在△ABC中,∠CAE=20°,∠C=40°,∠CBD=30°,求∠AFB的度数.
21.如果一个三角形的一边长为5cm,另一边长为2cm,若第三边长为x cm.
(1)第三边x的范围为 .
(2)当第三边长为奇数时,求出这个三角形的周长,并指出它是什么三角形(按边分类).
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,BE⊥AC于点E,AD与BE交于点F.
(1)求∠ABE的度数;
(2)若AD平分∠BAC,DG平分∠ADC,试说明DG∥BE.
23.如图,在△ABC中,AD,AE分别是边BC上的中线和高,AE=2cm,S△ABD=5cm2,求BC和DC的长.
24.如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交BC于点E,若∠B=80°,求∠BEA的度数.
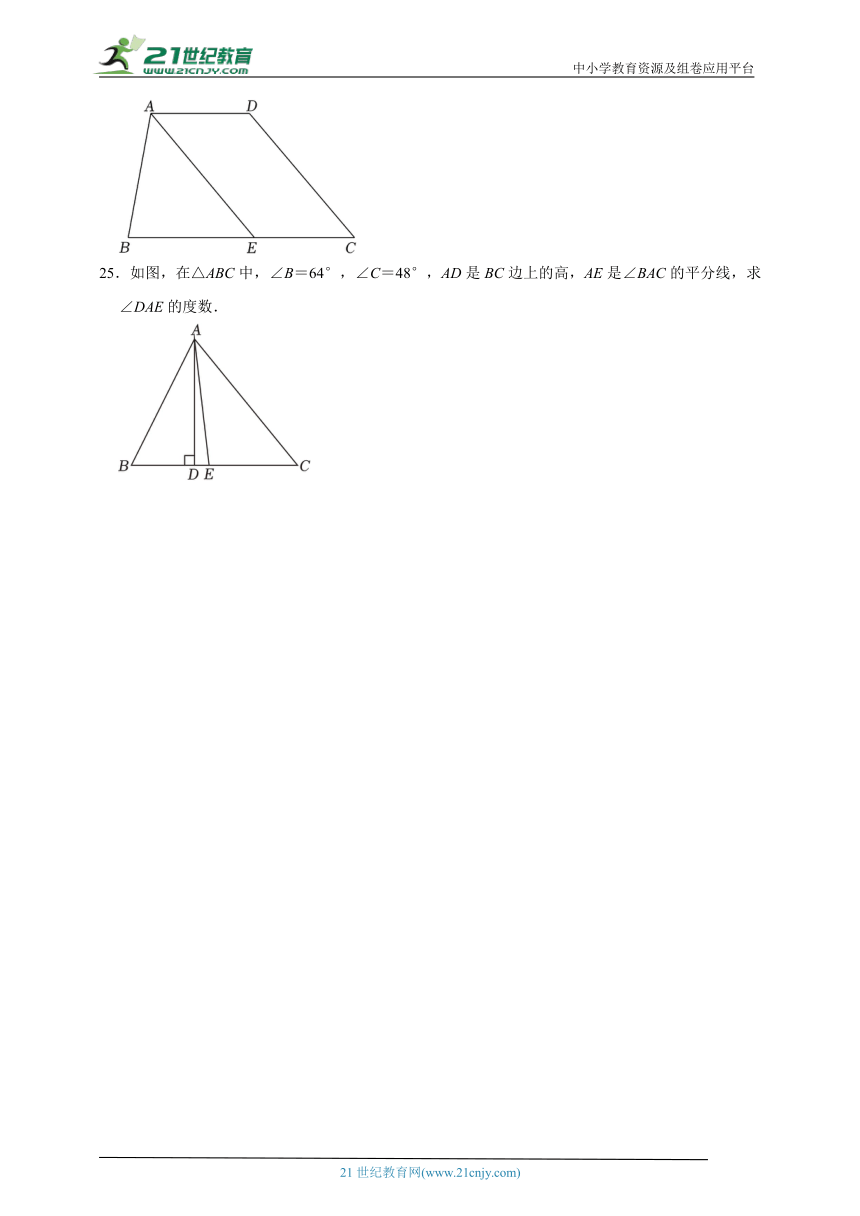
25.如图,在△ABC中,∠B=64°,∠C=48°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
认识三角形
参考答案与试题解析
一.选择题(共10小题)
1.【答案】D
【分析】在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形,由此即可判断.
【解答】解:A、3+3=6,长度是3、3、6的线段不能组成三角形,故A不符合题意;
B、5+6<12,长度是5、6、12的线段不能组成三角形,故B不符合题意;
C、2+5=7,长度是2、5、7的线段不能组成三角形,故C不符合题意;
D、6+7>8,长度是6、7、8的线段能组成三角形,故D符合题意.
故选:D.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
2.【答案】C
【分析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再选出答案.
【解答】解:设第三边长为x,由三角形三边关系定理得6﹣2<x<6+2,即4<x<8.
观察选项,只有选项C符合题意.
故选:C.
【点评】本题考查了三角形三边关系,此题实际上就是根据三角形三边关系定理列出不等式组,然后解不等式组即可.
3.【答案】A
【分析】利用三角形的三边关系进行分析即可.
【解答】解:∵OA=15米,OB=10米,
∴15﹣10<AB<15+10,
即:5<AB<25,
故选:A.
【点评】此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边,三角形的两边差小于第三边.
4.【答案】A
【分析】根据高线的定义可得∠AEC=90°,然后根据∠C=70°,∠ABC=48°求出∠CAB,再根据角平分线的定义求出∠1,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
【点评】本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.
5.【答案】B
【分析】根据三角形的面积公式以及三角形的中线定义,知三角形的一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
【解答】解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
【点评】考查了三角形的中线的概念.构造面积相等的两个三角形时,注意考虑三角形的中线.
6.【答案】B
【分析】本题可根据直角三角形内角的性质和三角形内角和为180°进行求解.
【解答】解:如图:∵AE、BD是直角三角形中两锐角平分线,
∴∠OAB+∠OBA=90°÷2=45°,
两角平分线组成的角有两个:∠BOE与∠EOD这两个角互补,
根据三角形外角和定理,∠BOE=∠OAB+∠OBA=45°,
∴∠EOD=180°﹣45°=135°,
故选:B.
【点评】本题考查的是直角三角形的性质,熟知直角三角形的性质是解答此题的关键.
7.【答案】A
【分析】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,由此即可解决问题.
【解答】解:设第3根木棒的长度是x cm,
∴5﹣3<x<5+3,
∴2<x<8,
∴不能围成一个三角形的是长为2cm木棒.
故选:A.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
8.【答案】B
【分析】根据三角形的中线把三角形分为面积相等的两部分解答.
【解答】解:由三角形的面积公式可知,三角形的中线把三角形分为面积相等的两部分,
∴他所作的线段AD应该是△ABC的中线,
故选:B.
【点评】本题考查的是三角形的面积计算,掌握三角形的中线把三角形分为面积相等的两部分是解题的关键.
9.【答案】D
【分析】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,设第三边长x,得到3<x<7,由△ABC的第三边长是偶数,得到x=4或6,于是得到此三角形的周长.
【解答】解:设第三边长x,
∴5﹣2<x<5+2,
∴3<x<7,
∵△ABC的第三边长是偶数,
∴x=4或6,
∴此三角形的周长为2+5+4=11或2+5+6=13.
故选:D.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
10.【答案】C
【分析】三角形两边之和大于第三边,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
【解答】解:A.由1cm、2cm,3cm,可得1+2=3,故不能组成三角形,不符合题意;
B.由6cm、2cm,3cm,可得2+3<6,故不能组成三角形,不符合题意;
C.由4cm、6cm,8cm,可得4+6>8,故能组成三角形,符合题意;
D.由5cm,6cm,12cm,可得5+6<12,故不能组成三角形,不符合题意.
故选:C.
【点评】本题主要考查了三角形三边关系,判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
二.填空题(共6小题)
11.【答案】45.
【分析】先由三角形的内角和定理求得∠BAC的度数,由角平分线的定义得出∠CAD的度数,再由平行线性质可得∠ACE的度数.
【解答】解:∵∠B=60°,∠ACB=30°,
∴∠BAC=180°﹣∠B﹣∠ACB=180°﹣60°﹣30°=90°,
∵AD是∠BAC的平分线,
∴∠CAD∠BAC90°=45°,
∵CE∥AD,
∴∠ACE=∠CAD=45°.
故答案为:45.
【点评】此题主要是考查了平行线的性质,三角形的内角的定理,角平分线定义,能够熟练掌握两直线平行,内错角相等是解答此题的关键.
12.【答案】58.
【分析】先根据AD⊥BD得出∠ADB=90°,故可得出∠BAD+∠ABD=90°,再由三角形内角和定理得出∠DBC的度数,由角平分线的定义得出∠ABC的度数,进而得出∠BAD的度数.
【解答】解:∵AD⊥BD,∠DAC=20°,∠C=38°,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠BAC+∠C+∠ABC=180°,即∠BAD+∠DAC+∠C+∠ABD+∠DBC=180°,
∴(∠BAD+∠ABD)+∠DAC+∠C+∠DBC=180°,即90°+20°+38°+∠DBC=180°,
∴∠DBC=32°,
∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC=32°,
∴∠BAD=90°﹣32°=58°.
故答案为:58.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解题的关键.
13.【答案】见试题解答内容
【分析】根据BD是△ABC的中线,可得,再由BG=2GD,可得,即可求解.
【解答】解:∵BD是△ABC的中线,△ABC的面积为6,
∴,
∵BG=2GD,
∴,
∴,
即图中阴影部分的面积是2.
故答案为:2.
【点评】本题考查三角形的面积问题.其中根据三角形的中线的性质进行解答是解决本题的关键.
14.【答案】116.
【分析】由图形可知∠A′NC=∠MNC﹣∠A′NM,故应设法求出∠MNC、∠A′NM的度数.由折叠的性质和三角形的内角和为180°,可以求出∠C的度数;然后再根据由MN∥BC得到∠ANM=∠C,∠CNM+∠C=180°,从而求出∠ANM和∠MNC的度数.由折叠的性质可知∠A′NM=∠ANM,进而解答题目.
【解答】解:根据折叠的性质可得∠A=∠A′=28°,∠A′NM=∠ANM.
∵∠A=28°,∠B=120°,
∴∠C=180°﹣∠A﹣∠B=32°.
∵MN∥BC,
∴∠ANM=∠C,∠CNM+∠C=180°.
∴∠CNM=180°﹣∠C=148°.
∵∠A′NM=∠ANM,∠ANM=∠C,
∴∠A′NM=∠C=32°.
∴∠A′NC=∠CNM﹣∠A′NM=148°﹣32°=116°.
故答案为:116.
【点评】本题考查三角形内角和定理,需要掌握平行线的性质和折叠的性质找出角之间的数量关系.
15.【答案】2.4.
【分析】根据直角三角形的面积公式计算即可.
【解答】解:∵∠ACB=90°,CD是斜边AB上的高,
∴,
∵AB=5,BC=4,AC=3,
∴5CD=3×4,
∴CD=2.4,
故答案为:2.4.
【点评】本题考查了直角三角形的面积,观察图形得出是解题的关键.
16.【答案】见试题解答内容
【分析】由平角的定义可求解∠BEC的度数,根据三角形的内角和定理可求解∠CBE的度数,结合角平分线的定义求得∠ABC的度数,再根据高线的定义可得∠ADB=90°,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵∠AEB=95°,
∴∠BEC=180°﹣95°=85°,
∵∠BEC+∠CBE+∠BCE=180°,∠C=70°,
∴∠CBE=180°﹣70°﹣85°=25°,
∵BE是∠ABC平分线,
∴∠ABC=2∠CBE=50°,
∵AD是高线,
∴∠ADB=90°,
∴∠BAD=180°﹣90°﹣50°=40°,
故答案为:40.
【点评】本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.
三.解答题(共9小题)
17.【答案】110°
【分析】首先利用三角形的内角和求出∠CAB=40°,然后利用角平分线的性质求出∠DAF=20°,最后利用三角形的外角与内角的关系及垂直的定义即可求解.
【解答】解:∵∠CAB=180°﹣∠ABC﹣∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
【点评】本题考查了三角形的内角和等于180°求解,是基础题,准确识别图形是解题的关键.
18.【答案】见试题解答内容
【分析】(1)根据三角形的第三边大于两边之差小于两边之和,即可解决问题;
(2)根据取值范围确定第三边,然后求得答案即可.
【解答】解:(1)∵三角形的第三边大于两边之差小于两边之和,
∴三角形的两边长分别是5、7,
则第三边长a的取值范围是2<a<12;
(2)∵a为整数,
∴当a=11时,组成的三角形的周长最大,
最大值是5+7+11=23.
【点评】本题考查了三角形的三边关系,解题的关键是了解两边之和大于第三边,两边之差小于第三边.
19.【答案】(1)∠CAE的度数为120°;
(2)∠MAE=2∠CAM﹣30°;
(3)m+n=60°.
【分析】(1)已知∠CAB=∠AED=90°,∠C=45°,∠EAD=30°,∠BAN=m°,∠DAN=n°,当m+n=0时,因为∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,所以可以直接计算出∠CAE的度数;
(2)根据三角形的余角和补角之间的关系,利用已知条件,可以得出∠CAM与∠MAE的数量关系;
(3)当点C,A,E三点共线时,此时∠CAE=180°,利用已知条件,可以探究出m与n的数量关系.
【解答】解:(1)∵∠CAB=∠AED=90°,∠C=45°,∠EAD=30°,∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150),
又∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴当m+n=0时,
∴∠CAE=90°+30°=120°,
答:∠CAE的度数为120°;
(2)∵MN是直线,∠CAB=∠AED=90°,∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150),
∴∠CAM=180°﹣90°﹣m°=90°﹣m°,
∴∠MAE=180°﹣30°﹣n°=150°﹣n°,
∵n=2m(m≠0),
∴∠MAE=2∠CAM﹣30°,
答:∠CAM与∠MAE的数量关系为:∠MAE=2∠CAM﹣30°;
(3)当点C,A,E三点共线时,
∵点C,A,E三点共线,
∴∠CAE=180°,
∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴180°=90°+30°+m+n,
∴m+n=60°,
答:m+n=60°.
【点评】考查重点是熟练掌握三角形的余角,补角的定义,学会利用三角形余角和补角之间的关系,进行综合运算.
20.【答案】见试题解答内容
【分析】根据三角形的内角和即可得到结论.
【解答】解:∵∠AEB=∠C+∠CAE,∠C=40°,∠CAE=20°,
∴∠AEB=60°.
∵∠CBD=30°,
∴∠BFE=180°﹣30°﹣60°=90°,
∴∠AFB=180°﹣∠BFE=90°.
【点评】本题考查了三角形的内角和,熟练掌握三角形的内角和是解题的关键.
21.【答案】见试题解答内容
【分析】(1)三角形两边的和大于第三边,三角形两边的差小于第三边,据此可求得答案.
(2)先求得第三边的长度,然后计算三角形的周长并按边的相等关系分类即可.
【解答】解:(1)根据三角形两边的和大于第三边,则
x<5+2.
即x<7.
根据三角形两边的差小于第三边,则
5﹣2<x.
即3<x.
综上所述
3<x<7.
故答案为:3<x<7.
(2)∵第三边的长为奇数,
∴第三边的长为5cm.
∴三角形的周长=5+5+2=12(cm).
∵两条边的长为5cm,另外一条边的长为2cm,
∴这个三角形是底边和腰不相等的等腰三角形.
【点评】本题主要考查三角形三边之间的大小关系以及三角形按边的相等关系分类,牢记三角形三边之间的大小关系(三角形两边的和大于第三边,三角形两边的差小于第三边)和三角形按边的相等关系分类是解题的关键.
22.【答案】(1)10°;(2)见解析.
【分析】(1)根据三角形内角和定理可得∠BAC的度数,再由垂直的定义及作角性质可得答案;
(2)由角平分线的定义和三角形内角和定理可得∠GDC=∠EBC.再根据平行线的判定方法可得结论.
【解答】解:(1)∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣40°=80°.
∵AC⊥BE,
∴∠AEB=90°,
∴∠ABE=90°﹣∠BAC=90°﹣80°=10°.
(2)∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=60°+40°=100°.
∵DG平分∠ADC,
∴.
∵∠EBC=∠ABC﹣∠ABE=60°﹣10°=50°,
∴∠EBC=∠GDC.
∴DG∥BE.
【点评】此题考查的是平行线的判定和三角形内角和定理,掌握其性质定理是解决此题的关键.
23.【答案】DC=5cm,BC=10cm.
【分析】利用得出BD的长,由AD是边BC上的中线即可得出BC和DC的长.
【解答】解:∵AE是△ABC中BC边上的高,且,
∴,
∵AE=2cm,
∴BD=5cm,
∵AD是△ABC中BC边上的中线,
∴DC=BD=5cm,BC=2BD=10cm.
【点评】此题主要考查了三角形的面积以及三角形中线以及高线的性质,解题的关键是掌握三角形的中线平分三角形的面积.
24.【答案】50°.
【分析】根据平行线的性质及角平分线的性质求得∠BAD的度数,然后根据三角形的内角和定理列式计算即可.
【解答】解:∵AD∥BC,∠B=80°,
∴∠BAD=180°﹣80°=100°,
∵AE平分∠BAD交BC于点E,
∴∠BAE∠BAD=50°,
∴∠BEA=180°﹣80°﹣50°=50°.
【点评】本题考查平行线性质,角平分线定义及三角形的内角和,结合已知条件求得∠BAE的度数是解题的关键.
25.【答案】∠DAE=8°.
【分析】根据三角形内角和定理求得∠BAC的度数,则∠EAC可求,然后在△ACD中,利用三角形内角和定理求得∠DAC的度数,根据∠DAE=∠DAC﹣∠EAC即可求解.
【解答】解:∵在△ABC中,∠B=64°,∠C=48°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣64°﹣48°=68°,
∵AE是∠BAC的平分线,
∴,
在直角△ADC中,∠DAC=90°﹣∠C=90°﹣48°=42°,
∴∠DAE=∠DAC﹣∠EAC=42°﹣34°=8°.
【点评】本题考查了三角形的内角和定理以及角平分线的定义,熟知三角形内角和是180°是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
认识三角形
一.选择题(共10小题)
1.下列三条线段的长度,能组成三角形的是( )
A.3,3,6 B.5,6,12 C.2,5,7 D.6,7,8
2.已知三角形的两条边长分别为2和6,则第三边的长可能是( )
A.1 B.2 C.7 D.9
3.如图,为估计池塘岸边A,B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
A.25米 B.15米 C.10米 D.6米
4.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
5.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
6.直角三角形两个锐角平分线相交所成的钝角的度数为( )
A.90° B.135° C.120° D.45°或135°
7.幼儿园的小朋友用木棒做拼图形游戏,一个孩子手中有2根木棒长度分别为3cm和5cm,下列木棒不能使其能围成一个三角形的是( )
A.2cm B.3cm C.4cm D.5cm
8.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
9.已知△ABC中,其中有两边长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为( )
A.11 B.12 C.13 D.11或13
10.下列长度的三条线段能组成三角形的是( )
A.1cm、2cm,3cm B.6cm、2cm,3cm
C.4cm、6cm,8cm D.5cm,6cm,12cm
二.填空题(共6小题)
11.如图,在△ABC中,AD是∠BAC的平分线,过点C的射线CE与AD平行,若∠B=60°,∠ACB=30°,则∠ACE= °.
12.如图,在△ABC中,已知BD是∠ABC的角平分线,点D是△ABC内一点,且AD⊥BD,∠DAC=20°,∠C=38°,那么∠BAD= °.
13.如图,BD是△ABC的中线,G是BD上的一点,且BG=2GD,连接AG,若△ABC的面积为6,则图中阴影部分的面积是 .
14.如图,点M,N分别在AB,AC上,MN∥BC,将△ABC沿MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC= °.
15.如图,在三角形ABC中,∠ACB=90°,CD是斜边AB上的高,若AB=5,BC=4,AC=3,则高CD的长度为 .
16.如图,△ABC中AD,BE分别是△ABC的高和角平分线,若∠C=70°,∠AEB=95°,则∠BAD= °.
三.解答题(共9小题)
17.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
18.已知三角形的两边长为5和7,第三边的边长a.
(1)求a的取值范围;
(2)若a为整数,当a为何值时,组成的三角形的周长最大,最大值是多少?
19.将一副三角板的两个顶点按图所示重叠摆放在直线MN上,且三角板ADE始终摆放在直线MN下方,三角板ABC可绕点A任意旋转.已知∠CAB=∠AED=90°,∠C=45°,∠EAD=30°.设∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150).
(1)当m+n=0时,求∠CAE的度数;
(2)当n=2m(m≠0)时,求∠CAM与∠MAE的数量关系;
(3)当点C,A,E三点共线时,请通过画图探究说明m与n的数量关系.
20.如图,在△ABC中,∠CAE=20°,∠C=40°,∠CBD=30°,求∠AFB的度数.
21.如果一个三角形的一边长为5cm,另一边长为2cm,若第三边长为x cm.
(1)第三边x的范围为 .
(2)当第三边长为奇数时,求出这个三角形的周长,并指出它是什么三角形(按边分类).
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,BE⊥AC于点E,AD与BE交于点F.
(1)求∠ABE的度数;
(2)若AD平分∠BAC,DG平分∠ADC,试说明DG∥BE.
23.如图,在△ABC中,AD,AE分别是边BC上的中线和高,AE=2cm,S△ABD=5cm2,求BC和DC的长.
24.如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交BC于点E,若∠B=80°,求∠BEA的度数.
25.如图,在△ABC中,∠B=64°,∠C=48°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
认识三角形
参考答案与试题解析
一.选择题(共10小题)
1.【答案】D
【分析】在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形,由此即可判断.
【解答】解:A、3+3=6,长度是3、3、6的线段不能组成三角形,故A不符合题意;
B、5+6<12,长度是5、6、12的线段不能组成三角形,故B不符合题意;
C、2+5=7,长度是2、5、7的线段不能组成三角形,故C不符合题意;
D、6+7>8,长度是6、7、8的线段能组成三角形,故D符合题意.
故选:D.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
2.【答案】C
【分析】根据在三角形中任意两边之和>第三边,任意两边之差<第三边;可求第三边长的范围,再选出答案.
【解答】解:设第三边长为x,由三角形三边关系定理得6﹣2<x<6+2,即4<x<8.
观察选项,只有选项C符合题意.
故选:C.
【点评】本题考查了三角形三边关系,此题实际上就是根据三角形三边关系定理列出不等式组,然后解不等式组即可.
3.【答案】A
【分析】利用三角形的三边关系进行分析即可.
【解答】解:∵OA=15米,OB=10米,
∴15﹣10<AB<15+10,
即:5<AB<25,
故选:A.
【点评】此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边,三角形的两边差小于第三边.
4.【答案】A
【分析】根据高线的定义可得∠AEC=90°,然后根据∠C=70°,∠ABC=48°求出∠CAB,再根据角平分线的定义求出∠1,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
【点评】本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.
5.【答案】B
【分析】根据三角形的面积公式以及三角形的中线定义,知三角形的一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
【解答】解:三角形一边上的中线把原三角形分成两个面积相等的三角形.
故选:B.
【点评】考查了三角形的中线的概念.构造面积相等的两个三角形时,注意考虑三角形的中线.
6.【答案】B
【分析】本题可根据直角三角形内角的性质和三角形内角和为180°进行求解.
【解答】解:如图:∵AE、BD是直角三角形中两锐角平分线,
∴∠OAB+∠OBA=90°÷2=45°,
两角平分线组成的角有两个:∠BOE与∠EOD这两个角互补,
根据三角形外角和定理,∠BOE=∠OAB+∠OBA=45°,
∴∠EOD=180°﹣45°=135°,
故选:B.
【点评】本题考查的是直角三角形的性质,熟知直角三角形的性质是解答此题的关键.
7.【答案】A
【分析】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,由此即可解决问题.
【解答】解:设第3根木棒的长度是x cm,
∴5﹣3<x<5+3,
∴2<x<8,
∴不能围成一个三角形的是长为2cm木棒.
故选:A.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
8.【答案】B
【分析】根据三角形的中线把三角形分为面积相等的两部分解答.
【解答】解:由三角形的面积公式可知,三角形的中线把三角形分为面积相等的两部分,
∴他所作的线段AD应该是△ABC的中线,
故选:B.
【点评】本题考查的是三角形的面积计算,掌握三角形的中线把三角形分为面积相等的两部分是解题的关键.
9.【答案】D
【分析】三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边,设第三边长x,得到3<x<7,由△ABC的第三边长是偶数,得到x=4或6,于是得到此三角形的周长.
【解答】解:设第三边长x,
∴5﹣2<x<5+2,
∴3<x<7,
∵△ABC的第三边长是偶数,
∴x=4或6,
∴此三角形的周长为2+5+4=11或2+5+6=13.
故选:D.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
10.【答案】C
【分析】三角形两边之和大于第三边,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
【解答】解:A.由1cm、2cm,3cm,可得1+2=3,故不能组成三角形,不符合题意;
B.由6cm、2cm,3cm,可得2+3<6,故不能组成三角形,不符合题意;
C.由4cm、6cm,8cm,可得4+6>8,故能组成三角形,符合题意;
D.由5cm,6cm,12cm,可得5+6<12,故不能组成三角形,不符合题意.
故选:C.
【点评】本题主要考查了三角形三边关系,判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.
二.填空题(共6小题)
11.【答案】45.
【分析】先由三角形的内角和定理求得∠BAC的度数,由角平分线的定义得出∠CAD的度数,再由平行线性质可得∠ACE的度数.
【解答】解:∵∠B=60°,∠ACB=30°,
∴∠BAC=180°﹣∠B﹣∠ACB=180°﹣60°﹣30°=90°,
∵AD是∠BAC的平分线,
∴∠CAD∠BAC90°=45°,
∵CE∥AD,
∴∠ACE=∠CAD=45°.
故答案为:45.
【点评】此题主要是考查了平行线的性质,三角形的内角的定理,角平分线定义,能够熟练掌握两直线平行,内错角相等是解答此题的关键.
12.【答案】58.
【分析】先根据AD⊥BD得出∠ADB=90°,故可得出∠BAD+∠ABD=90°,再由三角形内角和定理得出∠DBC的度数,由角平分线的定义得出∠ABC的度数,进而得出∠BAD的度数.
【解答】解:∵AD⊥BD,∠DAC=20°,∠C=38°,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠BAC+∠C+∠ABC=180°,即∠BAD+∠DAC+∠C+∠ABD+∠DBC=180°,
∴(∠BAD+∠ABD)+∠DAC+∠C+∠DBC=180°,即90°+20°+38°+∠DBC=180°,
∴∠DBC=32°,
∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC=32°,
∴∠BAD=90°﹣32°=58°.
故答案为:58.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解题的关键.
13.【答案】见试题解答内容
【分析】根据BD是△ABC的中线,可得,再由BG=2GD,可得,即可求解.
【解答】解:∵BD是△ABC的中线,△ABC的面积为6,
∴,
∵BG=2GD,
∴,
∴,
即图中阴影部分的面积是2.
故答案为:2.
【点评】本题考查三角形的面积问题.其中根据三角形的中线的性质进行解答是解决本题的关键.
14.【答案】116.
【分析】由图形可知∠A′NC=∠MNC﹣∠A′NM,故应设法求出∠MNC、∠A′NM的度数.由折叠的性质和三角形的内角和为180°,可以求出∠C的度数;然后再根据由MN∥BC得到∠ANM=∠C,∠CNM+∠C=180°,从而求出∠ANM和∠MNC的度数.由折叠的性质可知∠A′NM=∠ANM,进而解答题目.
【解答】解:根据折叠的性质可得∠A=∠A′=28°,∠A′NM=∠ANM.
∵∠A=28°,∠B=120°,
∴∠C=180°﹣∠A﹣∠B=32°.
∵MN∥BC,
∴∠ANM=∠C,∠CNM+∠C=180°.
∴∠CNM=180°﹣∠C=148°.
∵∠A′NM=∠ANM,∠ANM=∠C,
∴∠A′NM=∠C=32°.
∴∠A′NC=∠CNM﹣∠A′NM=148°﹣32°=116°.
故答案为:116.
【点评】本题考查三角形内角和定理,需要掌握平行线的性质和折叠的性质找出角之间的数量关系.
15.【答案】2.4.
【分析】根据直角三角形的面积公式计算即可.
【解答】解:∵∠ACB=90°,CD是斜边AB上的高,
∴,
∵AB=5,BC=4,AC=3,
∴5CD=3×4,
∴CD=2.4,
故答案为:2.4.
【点评】本题考查了直角三角形的面积,观察图形得出是解题的关键.
16.【答案】见试题解答内容
【分析】由平角的定义可求解∠BEC的度数,根据三角形的内角和定理可求解∠CBE的度数,结合角平分线的定义求得∠ABC的度数,再根据高线的定义可得∠ADB=90°,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵∠AEB=95°,
∴∠BEC=180°﹣95°=85°,
∵∠BEC+∠CBE+∠BCE=180°,∠C=70°,
∴∠CBE=180°﹣70°﹣85°=25°,
∵BE是∠ABC平分线,
∴∠ABC=2∠CBE=50°,
∵AD是高线,
∴∠ADB=90°,
∴∠BAD=180°﹣90°﹣50°=40°,
故答案为:40.
【点评】本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.
三.解答题(共9小题)
17.【答案】110°
【分析】首先利用三角形的内角和求出∠CAB=40°,然后利用角平分线的性质求出∠DAF=20°,最后利用三角形的外角与内角的关系及垂直的定义即可求解.
【解答】解:∵∠CAB=180°﹣∠ABC﹣∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
【点评】本题考查了三角形的内角和等于180°求解,是基础题,准确识别图形是解题的关键.
18.【答案】见试题解答内容
【分析】(1)根据三角形的第三边大于两边之差小于两边之和,即可解决问题;
(2)根据取值范围确定第三边,然后求得答案即可.
【解答】解:(1)∵三角形的第三边大于两边之差小于两边之和,
∴三角形的两边长分别是5、7,
则第三边长a的取值范围是2<a<12;
(2)∵a为整数,
∴当a=11时,组成的三角形的周长最大,
最大值是5+7+11=23.
【点评】本题考查了三角形的三边关系,解题的关键是了解两边之和大于第三边,两边之差小于第三边.
19.【答案】(1)∠CAE的度数为120°;
(2)∠MAE=2∠CAM﹣30°;
(3)m+n=60°.
【分析】(1)已知∠CAB=∠AED=90°,∠C=45°,∠EAD=30°,∠BAN=m°,∠DAN=n°,当m+n=0时,因为∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,所以可以直接计算出∠CAE的度数;
(2)根据三角形的余角和补角之间的关系,利用已知条件,可以得出∠CAM与∠MAE的数量关系;
(3)当点C,A,E三点共线时,此时∠CAE=180°,利用已知条件,可以探究出m与n的数量关系.
【解答】解:(1)∵∠CAB=∠AED=90°,∠C=45°,∠EAD=30°,∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150),
又∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴当m+n=0时,
∴∠CAE=90°+30°=120°,
答:∠CAE的度数为120°;
(2)∵MN是直线,∠CAB=∠AED=90°,∠BAN=m°,∠DAN=n° (0≤m≤180,0≤n≤150),
∴∠CAM=180°﹣90°﹣m°=90°﹣m°,
∴∠MAE=180°﹣30°﹣n°=150°﹣n°,
∵n=2m(m≠0),
∴∠MAE=2∠CAM﹣30°,
答:∠CAM与∠MAE的数量关系为:∠MAE=2∠CAM﹣30°;
(3)当点C,A,E三点共线时,
∵点C,A,E三点共线,
∴∠CAE=180°,
∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴180°=90°+30°+m+n,
∴m+n=60°,
答:m+n=60°.
【点评】考查重点是熟练掌握三角形的余角,补角的定义,学会利用三角形余角和补角之间的关系,进行综合运算.
20.【答案】见试题解答内容
【分析】根据三角形的内角和即可得到结论.
【解答】解:∵∠AEB=∠C+∠CAE,∠C=40°,∠CAE=20°,
∴∠AEB=60°.
∵∠CBD=30°,
∴∠BFE=180°﹣30°﹣60°=90°,
∴∠AFB=180°﹣∠BFE=90°.
【点评】本题考查了三角形的内角和,熟练掌握三角形的内角和是解题的关键.
21.【答案】见试题解答内容
【分析】(1)三角形两边的和大于第三边,三角形两边的差小于第三边,据此可求得答案.
(2)先求得第三边的长度,然后计算三角形的周长并按边的相等关系分类即可.
【解答】解:(1)根据三角形两边的和大于第三边,则
x<5+2.
即x<7.
根据三角形两边的差小于第三边,则
5﹣2<x.
即3<x.
综上所述
3<x<7.
故答案为:3<x<7.
(2)∵第三边的长为奇数,
∴第三边的长为5cm.
∴三角形的周长=5+5+2=12(cm).
∵两条边的长为5cm,另外一条边的长为2cm,
∴这个三角形是底边和腰不相等的等腰三角形.
【点评】本题主要考查三角形三边之间的大小关系以及三角形按边的相等关系分类,牢记三角形三边之间的大小关系(三角形两边的和大于第三边,三角形两边的差小于第三边)和三角形按边的相等关系分类是解题的关键.
22.【答案】(1)10°;(2)见解析.
【分析】(1)根据三角形内角和定理可得∠BAC的度数,再由垂直的定义及作角性质可得答案;
(2)由角平分线的定义和三角形内角和定理可得∠GDC=∠EBC.再根据平行线的判定方法可得结论.
【解答】解:(1)∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣40°=80°.
∵AC⊥BE,
∴∠AEB=90°,
∴∠ABE=90°﹣∠BAC=90°﹣80°=10°.
(2)∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=60°+40°=100°.
∵DG平分∠ADC,
∴.
∵∠EBC=∠ABC﹣∠ABE=60°﹣10°=50°,
∴∠EBC=∠GDC.
∴DG∥BE.
【点评】此题考查的是平行线的判定和三角形内角和定理,掌握其性质定理是解决此题的关键.
23.【答案】DC=5cm,BC=10cm.
【分析】利用得出BD的长,由AD是边BC上的中线即可得出BC和DC的长.
【解答】解:∵AE是△ABC中BC边上的高,且,
∴,
∵AE=2cm,
∴BD=5cm,
∵AD是△ABC中BC边上的中线,
∴DC=BD=5cm,BC=2BD=10cm.
【点评】此题主要考查了三角形的面积以及三角形中线以及高线的性质,解题的关键是掌握三角形的中线平分三角形的面积.
24.【答案】50°.
【分析】根据平行线的性质及角平分线的性质求得∠BAD的度数,然后根据三角形的内角和定理列式计算即可.
【解答】解:∵AD∥BC,∠B=80°,
∴∠BAD=180°﹣80°=100°,
∵AE平分∠BAD交BC于点E,
∴∠BAE∠BAD=50°,
∴∠BEA=180°﹣80°﹣50°=50°.
【点评】本题考查平行线性质,角平分线定义及三角形的内角和,结合已知条件求得∠BAE的度数是解题的关键.
25.【答案】∠DAE=8°.
【分析】根据三角形内角和定理求得∠BAC的度数,则∠EAC可求,然后在△ACD中,利用三角形内角和定理求得∠DAC的度数,根据∠DAE=∠DAC﹣∠EAC即可求解.
【解答】解:∵在△ABC中,∠B=64°,∠C=48°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣64°﹣48°=68°,
∵AE是∠BAC的平分线,
∴,
在直角△ADC中,∠DAC=90°﹣∠C=90°﹣48°=42°,
∴∠DAE=∠DAC﹣∠EAC=42°﹣34°=8°.
【点评】本题考查了三角形的内角和定理以及角平分线的定义,熟知三角形内角和是180°是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
