4.4利用三角形全等测距离(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 4.4利用三角形全等测距离(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 684.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 15:38:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
利用三角形全等测距离
一.选择题(共10小题)
1.如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具?( )
A.可以带1号去 B.可以带2号去
C.可以带3号去 D.都不行
2.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由旋转,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SSS B.SAS C.AAS D.ASA
3.如图,要测量池塘A,B两端的距离,作线段AC与BD相交于点O.若AC=BD=8m,AO=DO,△COD的周长为14m,则A,B两点间的距离为( )
A.6m B.8m C.10m D.12m
4.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块,小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,AC B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
5.如图,为了测量出池塘A、B两点之间的距离,小育在平地上选取了能够直接到达点A和点B的一点C.他连接BC并延长,使CE=BC;又连接AC并延长,使CD=AC,连接DE.只要测量出DE的长度,也就得到了A、B两点之间的距离,这样测量的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图,有两个长度相同的滑梯靠在一面竖直墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若DF=6m,DE=8m,AD=4m,则BF等于( )
A.18m B.16m C.12m D.10m
7.如图是雨伞在开合过程中某时刻的结构图,AB、AC是伞骨,DM,EM是连接弹簧和伞骨的支架,已知点D,E分别是AB,AC的中点,AB=AC,DM=EM.弹簧M在向上滑动的过程中,总有△ADM≌△AEM,其判定依据是( )
A.ASA B.AAS C.SSS D.HL
8.如图,把两根钢条AA',BB'的中点连在一起,可以做成一个测量工作内槽宽的卡钳,卡钳的工作原理是全等三角形的判定定理,其依据是( )
A.SSS B.SAS C.AAS D.ASA
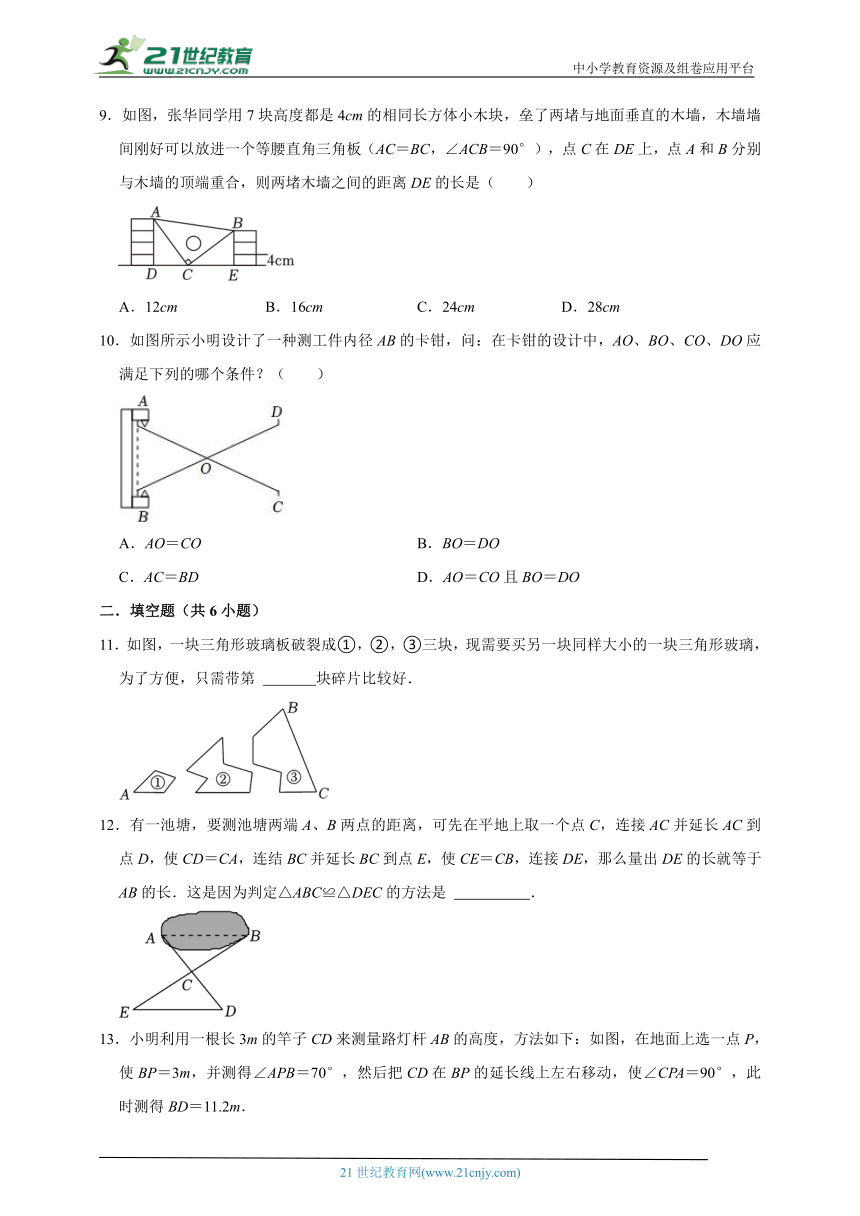
9.如图,张华同学用7块高度都是4cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙墙间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离DE的长是( )
A.12cm B.16cm C.24cm D.28cm
10.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO应满足下列的哪个条件?( )
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
二.填空题(共6小题)
11.如图,一块三角形玻璃板破裂成①,②,③三块,现需要买另一块同样大小的一块三角形玻璃,为了方便,只需带第 块碎片比较好.
12.有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个点C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长.这是因为判定△ABC≌△DEC的方法是 .
13.小明利用一根长3m的竿子CD来测量路灯杆AB的高度,方法如下:如图,在地面上选一点P,使BP=3m,并测得∠APB=70°,然后把CD在BP的延长线上左右移动,使∠CPA=90°,此时测得BD=11.2m.
(1)此时∠C的度数为 ;
(2)路灯杆AB的高度为 m.
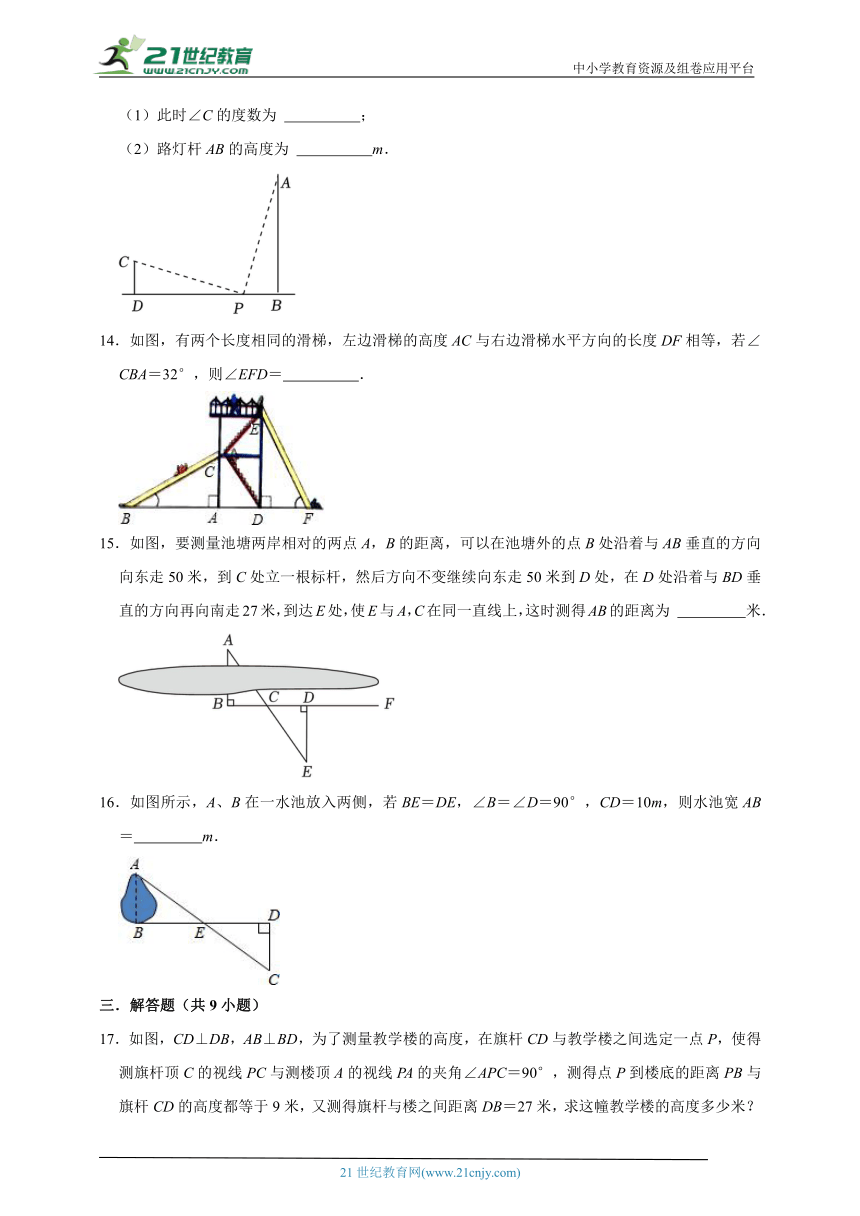
14.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,则∠EFD= .
15.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外的点B处沿着与AB垂直的方向向东走50米,到C处立一根标杆,然后方向不变继续向东走50米到D处,在D处沿着与BD垂直的方向再向南走27米,到达E处,使E与A,C在同一直线上,这时测得AB的距离为 米.
16.如图所示,A、B在一水池放入两侧,若BE=DE,∠B=∠D=90°,CD=10m,则水池宽AB= m.
三.解答题(共9小题)
17.如图,CD⊥DB,AB⊥BD,为了测量教学楼的高度,在旗杆CD与教学楼之间选定一点P,使得测旗杆顶C的视线PC与测楼顶A的视线PA的夹角∠APC=90°,测得点P到楼底的距离PB与旗杆CD的高度都等于9米,又测得旗杆与楼之间距离DB=27米,求这幢教学楼的高度多少米?
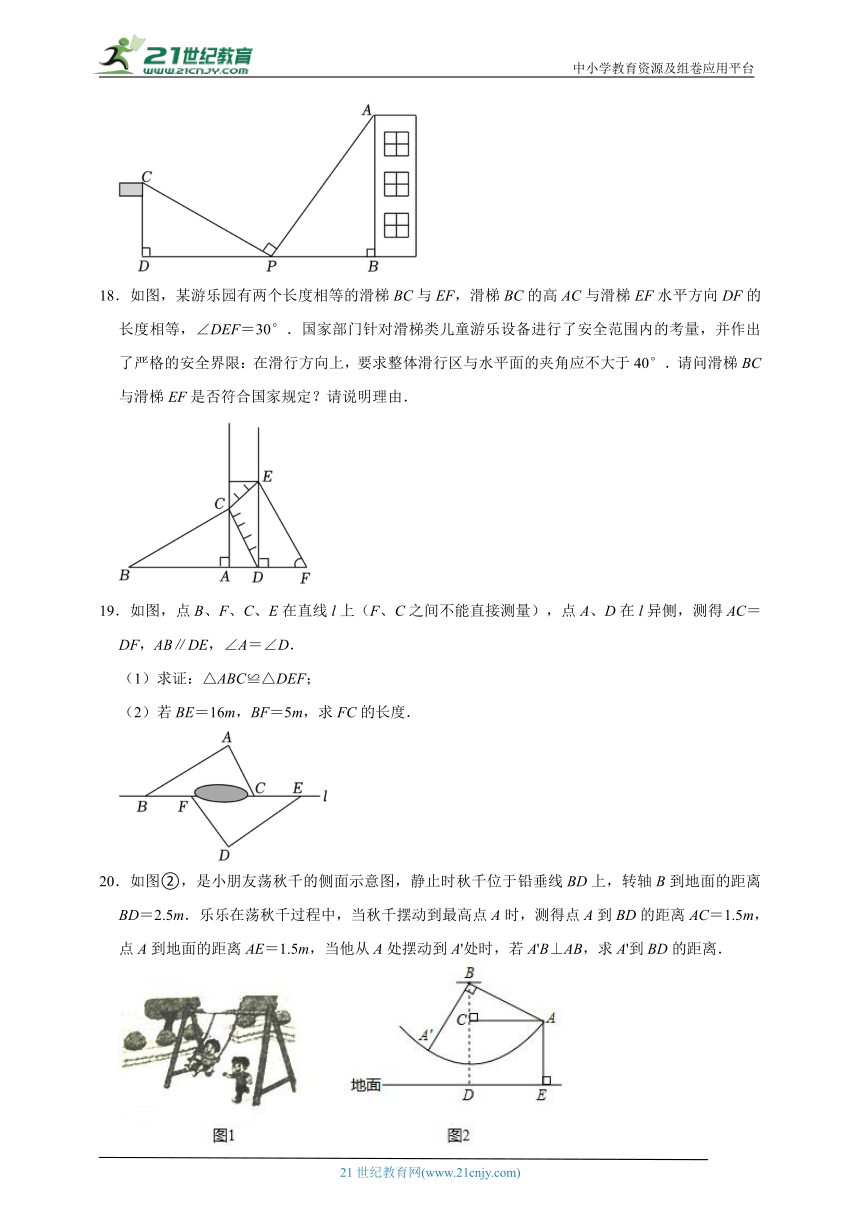
18.如图,某游乐园有两个长度相等的滑梯BC与EF,滑梯BC的高AC与滑梯EF水平方向DF的长度相等,∠DEF=30°.国家部门针对滑梯类儿童游乐设备进行了安全范围内的考量,并作出了严格的安全界限:在滑行方向上,要求整体滑行区与水平面的夹角应不大于40°.请问滑梯BC与滑梯EF是否符合国家规定?请说明理由.
19.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AC=DF,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=16m,BF=5m,求FC的长度.
20.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
21.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
22.小亮想测量屋前池塘的宽度,他结合所学的数学知识,设计了如图1的测量方案:先在池塘外的空地上任取一点O,连接AO,CO,并分别延长至点B,点D,使OB=OA,OD=OC,连接BD,
(1)如图1,求证:AC=BD;
(2)如图2,但在实际测量中,受地形条件的影响,于是小亮采取以下措施:延长CO至点D,使OC=OD,过点D作AC的平行线DE,延长AO至点F,连接EF,测得∠DEF=120°,∠OFE=90°,DE=5m,EF=9m,请求出池塘宽度AC.
23.如图,A,B两点位于高墙外,不能直接到达.为在该高楼的楼顶上搭建一个支架,需要在地面测量出A,B间的距离.学习了三角形全等知识后,小明给出了如下的方案:先在地面上取一点可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出CD的长度,CD的长度就是A,B间的距离.请根据以上的信息,说明AB=CD.
24.(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 ;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
25.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
利用三角形全等测距离
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】根据全等三角形的判定方法结合图形判断出带1号去.
【解答】解:由图形可知,1号有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带1号去.
故选:A.
【点评】本题考查了全等三角形的应用,熟练掌握全等三角形的判定方法是解题的关键.
2.【答案】B
【分析】由已知O是AA′、BB′的中点,再加上对顶角相等即可证明△OAB≌△OA′B′,利用SAS证明全等.
【解答】解:∵将两根钢条AA′、BB′的中点O连在一起,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
故选:B.
【点评】本题考查了三角形全等的判定方法,认真观察图形,选择合适的方法是解此题的关键.
3.【答案】A
【分析】证明△COD≌△BOA(SAS),则AB=CD,由△COD的周长为14m,可得OC+OD+CD=14,即AC+CD=14,计算求出CD的长,进而可得结果.
【解答】解:∵AC=BD,AO=DO,
∴AC﹣AO=BD﹣DO,即OC=OB,
∵OC=OB,∠COD=∠BOA,OD=OA,
∴△COD≌△BOA(SAS),
∴AB=CD,
∵△COD的周长为14m,
∴OC+OD+CD=14m,即AC+CD=14m,
∴CD=6m,
∴AB=6m,
故选:A.
【点评】本题考查了全等三角形的判定与性质.熟练掌握全等三角形的判定与性质是解题的关键.
4.【答案】C
【分析】直接利用全等三角形的判定方法分析得出答案.
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
【点评】此题主要考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
5.【答案】B
【分析】利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
【解答】解:在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴AB=DE.
故选:B.
【点评】本题考查了全等三角形的应用,把实际问题先转化为数学问题是解决问题的关键.
6.【答案】A
【分析】先根据“HL“定理判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质求出AB,即可求出BF.
【解答】解:由题意知,滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴AB=DE=8m,
∴BF=AB+AD+DF=8+4+6=18(m).
故选:A.
【点评】本题考查的是全等三角形的判定及性质,熟练掌握直角三角形全等的判定是解决问题的关键.
7.【答案】C
【分析】根据全等三角形判定的“SSS”定理即可证得△ADM≌△AEM.
【解答】解:∵AB=AC,点D,E分别是AB,AC的中点,
∴AD=AE,
在△ADM和△AEM中,
.
∴△ADM≌△AEM(SSS),
故选:C.
【点评】此题主要考查了全等三角形的应用,熟练掌握全等三角形的判定方法是解题关键.
8.【答案】B
【分析】卡钳的工作原理利用了三角形全等判定定理SAS,因为AA',BB'的中点O连在一起,因此OA=OA′,OB=OB′,还有对顶角相等,所以用的判定定理是边角边.
【解答】解:卡钳的工作原理利用了三角形全等判定定理SAS,理由如下:
∵O是AA',BB'的中点,
∴OA=OA′,OB=OB′,
又∵∠AOB=∠A'OB',
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
故选:B.
【点评】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.
9.【答案】D
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=16cm,DC=BE=12cm,
∴DE=DC+CE=28(cm),
即两堵木墙之间的距离为28cm.
故选:D.
【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
10.【答案】D
【分析】利用全等三角形的判定定理进行推理.
【解答】解:如图,连接CD,
已知对顶角∠AOB=∠COD,所以根据全等三角形的判定定理SAS可以判定△AOB≌△COD,由此推断AB=CD.
故选:D.
【点评】本题考查全等三角形的应用,根据已知条件可用边角边定理判断出全等.
二.填空题(共6小题)
11.【答案】③.
【分析】根据全等三角形的判定方法ASA即可判定.
【解答】解:只需带上③即可,因为③中,可以测量出三角形的两角以及夹边的大小,三角形的形状和大小是确定的,
故答案为:③.
【点评】本题主要考查了全等三角形的应用,灵活运用所学知识是解题的关键.
12.【答案】SAS.
【分析】利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
【解答】解:这是因为判定△ABC≌△DEC的方法是 SAS.故答案为:SAS.
【点评】本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
13.【答案】(1)70°;(2)8.2.
【分析】(1)找准对应角即可求得答案;
(2)根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB﹣PB求出即可.
【解答】解:(1)∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠C=∠APB=70°.
故答案为:70°;
(2)在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2m,BP=3m,
∴DP=BD﹣BP=8.2m,即AB=8.2m.
故答案为:8.2.
【点评】此题主要考查了全等三角形的应用,根据题意得出△CPD≌△PAB是解题关键.
14.【答案】见试题解答内容
【分析】利用“HL”证明△ABC和△DEF全等,根据全等三角形对应角相等可得∠EFD=∠BCA,再根据直角三角形两锐角互余求出∠BCA,即可得解.
【解答】解:∵两个滑梯的长度相同,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(HL),
∴∠EFD=∠BCA,
∵∠CBA=32°,
∴∠BCA=90°﹣32°=58°,
∴∠EFD=58°.
故答案为:58°.
【点评】本题考查了全等三角形的应用,直角三角形两锐角互余的性质,熟练掌握三角形全等的判定方法是解题的关键.
15.【答案】27.
【分析】利用ASA定理证明△ABC≌△EDC,根据全等三角形的对应边相等解答即可.
【解答】解:由题意得:CB=CD,∠ABC=∠EDC=90°,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA),
∴AB=DE=27米,
故答案为:27.
【点评】本题考查的是全等三角形的应用,掌握全等三角形的判定定理是解题的关键.
16.【答案】见试题解答内容
【分析】利用ASA得出△ABE≌△CDE(ASA),进而求出CD=AB即可得出答案.
【解答】解:在△ABE和△CDE中
,
∴△ABE≌△CDE(ASA),
∴CD=AB=10m.
故答案为:10.
【点评】此题主要考查了全等三角形的应用,根据题意熟练应用全等三角形的判定方法是解题关键.
三.解答题(共9小题)
17.【答案】18米.
【分析】根据AAS证明△DPC≌△BAP,从而利用全等三角形的性质可得AB=DP=18米.
【解答】解:∵CD⊥DB,AB⊥DB,
∴∠CDP=∠ABP=90°,
∵∠APC=90°,
∴∠CPD+∠APB=90°,∠PAB+∠APB=90°,
∴∠CPD=∠PAB,
∵DB=27米,PB=9米,
∴DP=BD﹣BP=18米,
在△DPC和△BAP中,
,
∴△DPC≌△BAP(AAS),
∴AB=DP=18米.
答:这幢教学楼的高度18米.
【点评】本题考查全等三角形的应用,熟练掌握全等三角形的判定与性质是解题的关键.
18.【答案】滑梯BC符合国家规定,滑梯EF不符合国家规定,理由见解析.
【分析】利用“HL”证明Rt△ABC和Rt△DEF全等,根据全等三角形对应角相等可得∠DEF=∠ABC=30°,再根据直角三角形两锐角互余求出∠DFE=60°,再根据题意判断即可得解.
【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=30°,
∴∠DFE=90°﹣30°=60°.
∵∠ABC<40°,∠DFE>40°,
∴滑梯BC符合国家规定,滑梯EF不符合国家规定.
【点评】本题考查了全等三角形的性质和判定,直角三角形两锐角互余的性质,准确识图判断出全等三角形是解题的关键.
19.【答案】(1)见解析;(2)6m.
【分析】(1)先证明∠ABC=∠DEF,再根据ASA即可证明.
(2)根据全等三角形的性质即可解答.
【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=16m,BF=5m,
∴FC=16﹣5﹣5=6(m).
【点评】本题考查全等三角形的判定和性质、平行线的判定等知识,解题的关键是正确寻找全等三角形的条件,记住平行线的判定方法,属于基础题,中考常考题型.
20.【答案】A'到BD的距离是1m.
【分析】作A'F⊥BD,垂足为F,根据全等三角形的判定和性质解答即可.
【解答】解:如图2,作A'F⊥BD,垂足为F.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°;
在Rt△A'FB中,∠1+∠3=90°;
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC
∵AC∥DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m.
【点评】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
21.【答案】这个人从B点到M点运动了3s.
【分析】根据∠CMD=90°,利用互余关系可以得出:∠ACM=∠DMB,证明三角形全等的另外两个条件容易看出.利用全等的性质可求得AC=BM=3,从而求得运动时间.
【解答】解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在△ACM和△BMD中,
,
∴△ACM≌△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
【点评】本题考查了全等三角形的应用;解答本题的关键是利用互余关系找三角形全等的条件,对应角相等,并巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.本题的关键是求得Rt△ACM≌Rt△BMD.
22.【答案】(1)见解答;
(2)23m.
【分析】(1)利用SAS证明△OAC≌△OBD即可;
(2)延长DE,AF交于点B,利用ASA证明出△OAC≌△OBD,得到AC=BD,由已知条件可以得到△BEF是含30°角的直角三角形,从而求出BE的长,进而求出BD的长,从而得到池塘宽度AC.
【解答】(1)证明:在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴AC=BD;
(2)解:延长DE,AF交于点B,
∵DE∥AC,
∴∠C=∠D,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(ASA),
∴AC=BD,
∵∠DEF=120°,∠OFE=90°,
∴∠BFE=90°,∠BEF=60°,∠B=30°,
∵EF=9m,
∴BE=2EF=18m,
∵DE=5m,
∴BD=BE+DE=23m,
∴AC=23m,
答:池塘宽度AC为23m.
【点评】本题考查全等三角形的判定和性质,含30°角直角三角形的性质,掌握全等三角形的判定方法,构造全等三角形是解题的关键.
23.【答案】答案见解答部分.
【分析】利用SAS证得△AOB≌△COD,则其对应边相等.
【解答】解:在△AOB与△COD中,
,
则△AOB≌△COD(SAS).
所以AB=CD.
【点评】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.
24.【答案】(1)三角形具有稳定性.
(2)BC=38cm,理由见解答.
【分析】(1)根据三角形的稳定性进行解答即可;
(2)证明△AOD≌△BOC(SAS),得BC=AD,结合已知条件则可知BC的长度
【解答】解:(1)由题意得,这种设计所运用的数学原理是三角形具有稳定性;
故答案为:三角形具有稳定性.
(2)CB=38cm.
理由如下:∵O是AB和CD的中点,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
又∵AD=38cm,
∴BC=AD=38cm.
【点评】本题考查了三角形的稳定性,三角形全等的性质与判定,证明△AOD≌△BOC是解题的关键.
25.【答案】两个排污口之间的水平距离DC为500米.
【分析】根据ASA证明△ADE与△ECB全等,再利用全等三角形的性质解答即可.
【解答】解:∵∠AEB=90°,AD⊥DC,BC⊥DC,
∴∠AEB=∠ADE=∠BCE=90°,
∴∠AED+∠DAE=90°,∠AED+∠BEC=90°,∠BEC+∠EBC=90°,
∴∠DAE=∠CEB,∠AED=∠EBC,
又∵AE=BE,
∴△ADE≌△ECB(ASA),
∴AD=CE,DE=BC,
又∵AD=150米,BC=350米,
∴DC=DE+CE=BC+AD=350+150=500(米).
答:两个排污口之间的水平距离DC为500米.
【点评】此题考查全等三角形的应用,关键是根据ASA证明△ADE与△ECB全等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
利用三角形全等测距离
一.选择题(共10小题)
1.如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具?( )
A.可以带1号去 B.可以带2号去
C.可以带3号去 D.都不行
2.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由旋转,就做成了一个测量工件,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SSS B.SAS C.AAS D.ASA
3.如图,要测量池塘A,B两端的距离,作线段AC与BD相交于点O.若AC=BD=8m,AO=DO,△COD的周长为14m,则A,B两点间的距离为( )
A.6m B.8m C.10m D.12m
4.如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块,小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,AC B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
5.如图,为了测量出池塘A、B两点之间的距离,小育在平地上选取了能够直接到达点A和点B的一点C.他连接BC并延长,使CE=BC;又连接AC并延长,使CD=AC,连接DE.只要测量出DE的长度,也就得到了A、B两点之间的距离,这样测量的依据是( )
A.SSS B.SAS C.ASA D.AAS
6.如图,有两个长度相同的滑梯靠在一面竖直墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若DF=6m,DE=8m,AD=4m,则BF等于( )
A.18m B.16m C.12m D.10m
7.如图是雨伞在开合过程中某时刻的结构图,AB、AC是伞骨,DM,EM是连接弹簧和伞骨的支架,已知点D,E分别是AB,AC的中点,AB=AC,DM=EM.弹簧M在向上滑动的过程中,总有△ADM≌△AEM,其判定依据是( )
A.ASA B.AAS C.SSS D.HL
8.如图,把两根钢条AA',BB'的中点连在一起,可以做成一个测量工作内槽宽的卡钳,卡钳的工作原理是全等三角形的判定定理,其依据是( )
A.SSS B.SAS C.AAS D.ASA
9.如图,张华同学用7块高度都是4cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙墙间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离DE的长是( )
A.12cm B.16cm C.24cm D.28cm
10.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO应满足下列的哪个条件?( )
A.AO=CO B.BO=DO
C.AC=BD D.AO=CO且BO=DO
二.填空题(共6小题)
11.如图,一块三角形玻璃板破裂成①,②,③三块,现需要买另一块同样大小的一块三角形玻璃,为了方便,只需带第 块碎片比较好.
12.有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个点C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长.这是因为判定△ABC≌△DEC的方法是 .
13.小明利用一根长3m的竿子CD来测量路灯杆AB的高度,方法如下:如图,在地面上选一点P,使BP=3m,并测得∠APB=70°,然后把CD在BP的延长线上左右移动,使∠CPA=90°,此时测得BD=11.2m.
(1)此时∠C的度数为 ;
(2)路灯杆AB的高度为 m.
14.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,则∠EFD= .
15.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外的点B处沿着与AB垂直的方向向东走50米,到C处立一根标杆,然后方向不变继续向东走50米到D处,在D处沿着与BD垂直的方向再向南走27米,到达E处,使E与A,C在同一直线上,这时测得AB的距离为 米.
16.如图所示,A、B在一水池放入两侧,若BE=DE,∠B=∠D=90°,CD=10m,则水池宽AB= m.
三.解答题(共9小题)
17.如图,CD⊥DB,AB⊥BD,为了测量教学楼的高度,在旗杆CD与教学楼之间选定一点P,使得测旗杆顶C的视线PC与测楼顶A的视线PA的夹角∠APC=90°,测得点P到楼底的距离PB与旗杆CD的高度都等于9米,又测得旗杆与楼之间距离DB=27米,求这幢教学楼的高度多少米?
18.如图,某游乐园有两个长度相等的滑梯BC与EF,滑梯BC的高AC与滑梯EF水平方向DF的长度相等,∠DEF=30°.国家部门针对滑梯类儿童游乐设备进行了安全范围内的考量,并作出了严格的安全界限:在滑行方向上,要求整体滑行区与水平面的夹角应不大于40°.请问滑梯BC与滑梯EF是否符合国家规定?请说明理由.
19.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AC=DF,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=16m,BF=5m,求FC的长度.
20.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
21.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
22.小亮想测量屋前池塘的宽度,他结合所学的数学知识,设计了如图1的测量方案:先在池塘外的空地上任取一点O,连接AO,CO,并分别延长至点B,点D,使OB=OA,OD=OC,连接BD,
(1)如图1,求证:AC=BD;
(2)如图2,但在实际测量中,受地形条件的影响,于是小亮采取以下措施:延长CO至点D,使OC=OD,过点D作AC的平行线DE,延长AO至点F,连接EF,测得∠DEF=120°,∠OFE=90°,DE=5m,EF=9m,请求出池塘宽度AC.
23.如图,A,B两点位于高墙外,不能直接到达.为在该高楼的楼顶上搭建一个支架,需要在地面测量出A,B间的距离.学习了三角形全等知识后,小明给出了如下的方案:先在地面上取一点可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并测量出CD的长度,CD的长度就是A,B间的距离.请根据以上的信息,说明AB=CD.
24.(1)萧县某中学计划为学生暑期军训配备如图(1)所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是 ;
(2)图(2)是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,交点O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为38cm,则由以上信息可推得CB的长度是多少?请说明理由.
25.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A和B,AD、BC的长表示两个工厂到河岸的距离,其中E是进水口,D、C为两个排污口.已知AE=BE,∠AEB=90°,AD⊥DC,BC⊥DC,点D、E、C在同一直线上,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
利用三角形全等测距离
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】根据全等三角形的判定方法结合图形判断出带1号去.
【解答】解:由图形可知,1号有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带1号去.
故选:A.
【点评】本题考查了全等三角形的应用,熟练掌握全等三角形的判定方法是解题的关键.
2.【答案】B
【分析】由已知O是AA′、BB′的中点,再加上对顶角相等即可证明△OAB≌△OA′B′,利用SAS证明全等.
【解答】解:∵将两根钢条AA′、BB′的中点O连在一起,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
故选:B.
【点评】本题考查了三角形全等的判定方法,认真观察图形,选择合适的方法是解此题的关键.
3.【答案】A
【分析】证明△COD≌△BOA(SAS),则AB=CD,由△COD的周长为14m,可得OC+OD+CD=14,即AC+CD=14,计算求出CD的长,进而可得结果.
【解答】解:∵AC=BD,AO=DO,
∴AC﹣AO=BD﹣DO,即OC=OB,
∵OC=OB,∠COD=∠BOA,OD=OA,
∴△COD≌△BOA(SAS),
∴AB=CD,
∵△COD的周长为14m,
∴OC+OD+CD=14m,即AC+CD=14m,
∴CD=6m,
∴AB=6m,
故选:A.
【点评】本题考查了全等三角形的判定与性质.熟练掌握全等三角形的判定与性质是解题的关键.
4.【答案】C
【分析】直接利用全等三角形的判定方法分析得出答案.
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
【点评】此题主要考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
5.【答案】B
【分析】利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
【解答】解:在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴AB=DE.
故选:B.
【点评】本题考查了全等三角形的应用,把实际问题先转化为数学问题是解决问题的关键.
6.【答案】A
【分析】先根据“HL“定理判断出Rt△ABC≌Rt△DEF,再根据全等三角形的性质求出AB,即可求出BF.
【解答】解:由题意知,滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴AB=DE=8m,
∴BF=AB+AD+DF=8+4+6=18(m).
故选:A.
【点评】本题考查的是全等三角形的判定及性质,熟练掌握直角三角形全等的判定是解决问题的关键.
7.【答案】C
【分析】根据全等三角形判定的“SSS”定理即可证得△ADM≌△AEM.
【解答】解:∵AB=AC,点D,E分别是AB,AC的中点,
∴AD=AE,
在△ADM和△AEM中,
.
∴△ADM≌△AEM(SSS),
故选:C.
【点评】此题主要考查了全等三角形的应用,熟练掌握全等三角形的判定方法是解题关键.
8.【答案】B
【分析】卡钳的工作原理利用了三角形全等判定定理SAS,因为AA',BB'的中点O连在一起,因此OA=OA′,OB=OB′,还有对顶角相等,所以用的判定定理是边角边.
【解答】解:卡钳的工作原理利用了三角形全等判定定理SAS,理由如下:
∵O是AA',BB'的中点,
∴OA=OA′,OB=OB′,
又∵∠AOB=∠A'OB',
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
故选:B.
【点评】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.
9.【答案】D
【分析】根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
【解答】解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=16cm,DC=BE=12cm,
∴DE=DC+CE=28(cm),
即两堵木墙之间的距离为28cm.
故选:D.
【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.
10.【答案】D
【分析】利用全等三角形的判定定理进行推理.
【解答】解:如图,连接CD,
已知对顶角∠AOB=∠COD,所以根据全等三角形的判定定理SAS可以判定△AOB≌△COD,由此推断AB=CD.
故选:D.
【点评】本题考查全等三角形的应用,根据已知条件可用边角边定理判断出全等.
二.填空题(共6小题)
11.【答案】③.
【分析】根据全等三角形的判定方法ASA即可判定.
【解答】解:只需带上③即可,因为③中,可以测量出三角形的两角以及夹边的大小,三角形的形状和大小是确定的,
故答案为:③.
【点评】本题主要考查了全等三角形的应用,灵活运用所学知识是解题的关键.
12.【答案】SAS.
【分析】利用“边角边”证明△ABC和△DEC全等,再根据全等三角形对应边相等解答.
【解答】解:这是因为判定△ABC≌△DEC的方法是 SAS.故答案为:SAS.
【点评】本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.
13.【答案】(1)70°;(2)8.2.
【分析】(1)找准对应角即可求得答案;
(2)根据题意可得△CPD≌△PAB(ASA),进而利用AB=DP=DB﹣PB求出即可.
【解答】解:(1)∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠C=∠APB=70°.
故答案为:70°;
(2)在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2m,BP=3m,
∴DP=BD﹣BP=8.2m,即AB=8.2m.
故答案为:8.2.
【点评】此题主要考查了全等三角形的应用,根据题意得出△CPD≌△PAB是解题关键.
14.【答案】见试题解答内容
【分析】利用“HL”证明△ABC和△DEF全等,根据全等三角形对应角相等可得∠EFD=∠BCA,再根据直角三角形两锐角互余求出∠BCA,即可得解.
【解答】解:∵两个滑梯的长度相同,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(HL),
∴∠EFD=∠BCA,
∵∠CBA=32°,
∴∠BCA=90°﹣32°=58°,
∴∠EFD=58°.
故答案为:58°.
【点评】本题考查了全等三角形的应用,直角三角形两锐角互余的性质,熟练掌握三角形全等的判定方法是解题的关键.
15.【答案】27.
【分析】利用ASA定理证明△ABC≌△EDC,根据全等三角形的对应边相等解答即可.
【解答】解:由题意得:CB=CD,∠ABC=∠EDC=90°,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA),
∴AB=DE=27米,
故答案为:27.
【点评】本题考查的是全等三角形的应用,掌握全等三角形的判定定理是解题的关键.
16.【答案】见试题解答内容
【分析】利用ASA得出△ABE≌△CDE(ASA),进而求出CD=AB即可得出答案.
【解答】解:在△ABE和△CDE中
,
∴△ABE≌△CDE(ASA),
∴CD=AB=10m.
故答案为:10.
【点评】此题主要考查了全等三角形的应用,根据题意熟练应用全等三角形的判定方法是解题关键.
三.解答题(共9小题)
17.【答案】18米.
【分析】根据AAS证明△DPC≌△BAP,从而利用全等三角形的性质可得AB=DP=18米.
【解答】解:∵CD⊥DB,AB⊥DB,
∴∠CDP=∠ABP=90°,
∵∠APC=90°,
∴∠CPD+∠APB=90°,∠PAB+∠APB=90°,
∴∠CPD=∠PAB,
∵DB=27米,PB=9米,
∴DP=BD﹣BP=18米,
在△DPC和△BAP中,
,
∴△DPC≌△BAP(AAS),
∴AB=DP=18米.
答:这幢教学楼的高度18米.
【点评】本题考查全等三角形的应用,熟练掌握全等三角形的判定与性质是解题的关键.
18.【答案】滑梯BC符合国家规定,滑梯EF不符合国家规定,理由见解析.
【分析】利用“HL”证明Rt△ABC和Rt△DEF全等,根据全等三角形对应角相等可得∠DEF=∠ABC=30°,再根据直角三角形两锐角互余求出∠DFE=60°,再根据题意判断即可得解.
【解答】解:在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠DEF=∠ABC=30°,
∴∠DFE=90°﹣30°=60°.
∵∠ABC<40°,∠DFE>40°,
∴滑梯BC符合国家规定,滑梯EF不符合国家规定.
【点评】本题考查了全等三角形的性质和判定,直角三角形两锐角互余的性质,准确识图判断出全等三角形是解题的关键.
19.【答案】(1)见解析;(2)6m.
【分析】(1)先证明∠ABC=∠DEF,再根据ASA即可证明.
(2)根据全等三角形的性质即可解答.
【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=16m,BF=5m,
∴FC=16﹣5﹣5=6(m).
【点评】本题考查全等三角形的判定和性质、平行线的判定等知识,解题的关键是正确寻找全等三角形的条件,记住平行线的判定方法,属于基础题,中考常考题型.
20.【答案】A'到BD的距离是1m.
【分析】作A'F⊥BD,垂足为F,根据全等三角形的判定和性质解答即可.
【解答】解:如图2,作A'F⊥BD,垂足为F.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°;
在Rt△A'FB中,∠1+∠3=90°;
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC
∵AC∥DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m.
【点评】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
21.【答案】这个人从B点到M点运动了3s.
【分析】根据∠CMD=90°,利用互余关系可以得出:∠ACM=∠DMB,证明三角形全等的另外两个条件容易看出.利用全等的性质可求得AC=BM=3,从而求得运动时间.
【解答】解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在△ACM和△BMD中,
,
∴△ACM≌△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
【点评】本题考查了全等三角形的应用;解答本题的关键是利用互余关系找三角形全等的条件,对应角相等,并巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.本题的关键是求得Rt△ACM≌Rt△BMD.
22.【答案】(1)见解答;
(2)23m.
【分析】(1)利用SAS证明△OAC≌△OBD即可;
(2)延长DE,AF交于点B,利用ASA证明出△OAC≌△OBD,得到AC=BD,由已知条件可以得到△BEF是含30°角的直角三角形,从而求出BE的长,进而求出BD的长,从而得到池塘宽度AC.
【解答】(1)证明:在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴AC=BD;
(2)解:延长DE,AF交于点B,
∵DE∥AC,
∴∠C=∠D,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(ASA),
∴AC=BD,
∵∠DEF=120°,∠OFE=90°,
∴∠BFE=90°,∠BEF=60°,∠B=30°,
∵EF=9m,
∴BE=2EF=18m,
∵DE=5m,
∴BD=BE+DE=23m,
∴AC=23m,
答:池塘宽度AC为23m.
【点评】本题考查全等三角形的判定和性质,含30°角直角三角形的性质,掌握全等三角形的判定方法,构造全等三角形是解题的关键.
23.【答案】答案见解答部分.
【分析】利用SAS证得△AOB≌△COD,则其对应边相等.
【解答】解:在△AOB与△COD中,
,
则△AOB≌△COD(SAS).
所以AB=CD.
【点评】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.
24.【答案】(1)三角形具有稳定性.
(2)BC=38cm,理由见解答.
【分析】(1)根据三角形的稳定性进行解答即可;
(2)证明△AOD≌△BOC(SAS),得BC=AD,结合已知条件则可知BC的长度
【解答】解:(1)由题意得,这种设计所运用的数学原理是三角形具有稳定性;
故答案为:三角形具有稳定性.
(2)CB=38cm.
理由如下:∵O是AB和CD的中点,
∴AO=BO,CO=DO,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
又∵AD=38cm,
∴BC=AD=38cm.
【点评】本题考查了三角形的稳定性,三角形全等的性质与判定,证明△AOD≌△BOC是解题的关键.
25.【答案】两个排污口之间的水平距离DC为500米.
【分析】根据ASA证明△ADE与△ECB全等,再利用全等三角形的性质解答即可.
【解答】解:∵∠AEB=90°,AD⊥DC,BC⊥DC,
∴∠AEB=∠ADE=∠BCE=90°,
∴∠AED+∠DAE=90°,∠AED+∠BEC=90°,∠BEC+∠EBC=90°,
∴∠DAE=∠CEB,∠AED=∠EBC,
又∵AE=BE,
∴△ADE≌△ECB(ASA),
∴AD=CE,DE=BC,
又∵AD=150米,BC=350米,
∴DC=DE+CE=BC+AD=350+150=500(米).
答:两个排污口之间的水平距离DC为500米.
【点评】此题考查全等三角形的应用,关键是根据ASA证明△ADE与△ECB全等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
