12.3 一次函数与二元一次方程(共60张PPT)2025年秋沪科版八年级数学上册
文档属性
| 名称 | 12.3 一次函数与二元一次方程(共60张PPT)2025年秋沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 09:36:30 | ||
图片预览










文档简介
(共60张PPT)
12.3 一次函数与二元一次方程
第1课时
1.会用等量代换,把二元一次方程转化成一次函数.
2.知道一次函数上的点对应二元一次方程的解.
3.能判断点的坐标是否为二元一次方程的解.
◎重点:二元一次方程和一次函数的相互关系.
◎难点:体会数学中的等价思想.
同学们,还记得等式的性质吗?对于二元一次方程3x+5y=8,能不能将其转化为y=kx+b的形式呢?这就是本节课要学习的一次函数与二元一次方程的关系.
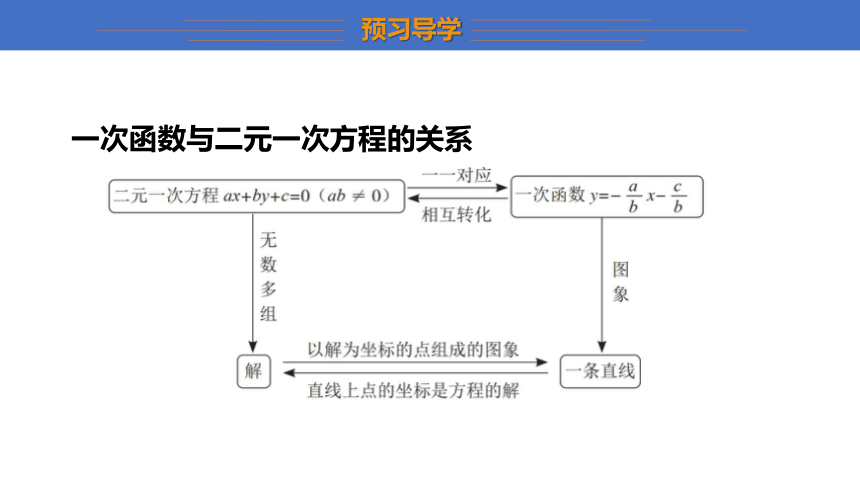
一次函数与二元一次方程的关系
阅读教材本课时所有内容,解决下列问题.
直线上任意一个点的坐标与其所对应的二元一次方程的解有什么关系?
一次函数所在的直线上任意一点的坐标都是其对应的二元一次方程的解.
一次函数与二元一次方程的关系
学法指导:一次函数的一部分可以转化为一元一次方程或一元一次不等式,通过观察一次函数的图象可以得到转化后的方程与不等式的解;而一次函数与其对应的二元一次方程更多的是等价的关系,一次函数上所有的点对应的有序数对(x,y)都是其对应的二元一次方程的解.
1.下列有序实数对中,对应二元一次方程2x+3y=7的解的是( B )
A. (1,2) B.(2,1)
C.(-1,-2) D. (-2,-1)
B
2.已知x=2是方程kx+b=0的解,则一次函数y=kx+b与x轴的交点坐标为( A )
A.(2,0) B.(0,2)
C.(-2,0) D.(0,-2)
3.把二元一次方程2x-y-3=0写成一次函数y= 2x-3 ;把一次函数y=6-2x写成二元一次方程为 2x+y=6 .
A
2x-3
2x+y=6
一次函数与二元一次方程的转化
1.把方程x+1=4y+化为y=kx+b的形式,正确的是
( B )
A.y=x+1 B.y=x+
C.y=x+1 D.y=x+
B
2.方程x+y=4的解有 无数 个,以方程x+y=4的解为坐标的点组成的图象与函数y=-x的图象的位置关系是 平行 .
无数
平行
3.在直角坐标系中画出方程2x+y-6=0的图象l1和方程x-y-3=0的图象l2,设l1与l2相交于点P,写出点P的坐标.
解:如图,交点P的坐标为(3,0).
【方法归纳交流】画二元一次方程的图象,其实质就是把二元一次方程化简成一次函数的形式,画出该一次函数的图象即可.
【变式训练】把二元一次方程5x+y-2=0的图象向上平移3个单位后,所得函数解析式是 y=-5x+5 .
y=-5x+5
4.已知二元一次方程3x-y-2=0所在的直线,在平面直角坐标系中与两坐标轴交于两点A、B,O为坐标原点,求三角形AOB的面积.
解:因为3x-y-2=0,所以y=3x-2,所以A、B的坐标为(,0),(0,-2),
所以三角形AOB的面积是××2=.
【变式训练】在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是
( B )
A.(0,) B.(0,)
C.(0,3) D.(0,4)
B
1.已知二元一次方程x+y=3与3x-y=5有一组公共解那么一次函数y=3-x与y=3x-5的图象的交点坐标为
( B )
A.(1,2) B.(2,1)
C.(-1,2) D.(-2,1)
B
2.若函数y=-x+a与y=4x-1的图象交于x轴上一点,求a的值.
解:因为函数y=-x+a与y=4x-1的图象交于x轴上一点,所以令两方程中y=0,即x=a=.
教科书第50页练习
12.3 一次函数与二元一次方程
第2课时
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组.
2.通过一次函数,了解二元一次方程组无解的情形.
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
◎重点:用图象法解二元一次方程组.
◎难点:用函数的观点看待方程,利用函数解决问题.
两条直线可能相交,只有一个交点;可能平行,没有交点;可能重合,有无数个交点.上节课,我们知道一次函数上的点对应二元一次方程的解,那么,两个一次函数的交点坐标对应的是不是两个二元一次方程的公共解呢?
二元一次方程组的图象解法
阅读教材本课时“例1”~“例3”,解决下列问题.
用作图法来解一元二次方程组的步骤是怎样的?
(1)转化形式:把二元一次方程化为一次函数的形式;(2)画函数图象:在同一直角坐标系中画出两个一次函数的图象,并确定交点坐标;(3)写出方程组的解:两条直线的交点坐标就是方程组的解.
1. 一次函数与二元一次方程组的对应关系
二元一次方程组两个一次函数两条直线;
二元一次方程组的解两个一次函数值相等时的自变量值及函数值两条直线的交点坐标.
2. 用图象法求二元一次方程组的解的一般步骤
(1)变函数:把方程组化为一次函数y=k1x+b1与y=k2x+b2;
(2)画图象:建立平面直角坐标系,画出两个一次函数的图象;
(3)找交点:由图象确定两直线交点的坐标;
(4)写结论:依据点的坐标写出方程组的解.
学法指导:利用一次函数的图象求对应的二元一次方程组的解比较麻烦,事实上,我们通常都是利用解二元一次方程组来求两条直线的交点坐标.
二元一次方程组解的情况的判断
阅读教材本课时“思考”中的内容,解决下列问题.
1.明晰概念:一次函数图象(两条直线)位置有三种关系及对应解的情况:
(1)相交(有一个交点) 二元一次方程组有 唯一解 ;
(2)平行(无交点) 二元一次方程组 无解 ;
(3)重合(有无数个交点) 二元一次方程组有 无数个解 .
唯一解
无解
无数个
解
2.直线y1=k1x+b1与直线y2=k2x+b2(k1≠0,k2≠0)不同系数情况下的位置关系.
①k1≠k2 y1与y2相交;
② y1与y2相交于y轴上同一点(0,b1)或(0,b2);
③ y1与y2平行;
④ y1与y2重合.
下面的二元一次方程组中方程无解的是( C )
A. B.
C. D.
C
用图象法解二次一次方程组
1.用图象法解方程组下图中正确的是( C )
A B
C
C D
【变式训练】用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图),则所解的二元一次方程组是( D )
D
A. B.
C. D.
2.如图,函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的的二元一次方程组的解是 .
利用方程组求两直线交点
3.求直线y=2x+4与y=-x+1的交点坐标.
解:由题意,得方程组
解这个方程组,得即交点坐标为(-1,2).
【方法归纳交流】在利用解方程组求两条直线y=k1x+b1和y=k2x+b2的交点坐标时,可直接消去y,得到k1x+b1=k2x+b2.在求得的解中,自变量的值作为横坐标,函数值作为纵坐标,要防止坐标顺序错误.
【变式训练】有两条直线y=ax+b和y=cx+5,学生甲求得它们的交点坐标为(3,-2),学生乙因看错c而求得它们的交点为(4,5),求两条直线的表达式.
解:把(3,-2)代入y=cx+5,得c=-.由点(4,5)和点(3,-2)都在函数y=ax+b上,所以有解得a=7,b=-23.所求的函数表达式为y=7x-23和y=-x+5.
两直线的位置关系与方程组的解
4.一次函数y=2x-1与y=2x+3的图象是两条 平行 (填“相交”或“平行”)的直线,因此方程组的解的情况是 无解 .
平行
无解
【变式训练】无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在( C )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
二元一次方程组的解与两直线l1:a1x+b1y=c1与l2:a2x+b2y=c2位置关系的联系(其中6 个常数均不为零):
从“数”看 从“形”看
≠ 方程组有唯一解 l1与l2相交
= ≠ 方程组无解 l1与l2平行
== 方程组有无数个解 l1与l2重合
1.当k>时,直线kx-y=k与直线ky+x=2k的交点在
( A )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
2.如图,直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P.求三角形APB的面积.
解:由题意得方程组
解得
所以点P坐标为(-1,-1),
所以S三角形ABP==.
教科书第52页练习
12.3 一次函数与二元一次方程
第3课时
学习目标
1.深入了解一次函数的应用价值.
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.
3.从问题的解决与探究中进一步感悟函数的应用价值,培养解决实际问题的数学能力.
4.通过从实际问题中得到函数关系式这一过程,提升学生的数学应用能力,使学生在探索过程中体验成功的喜悦,树立学习的自信心.
方案决策
情境引入
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清晰地认识各种方案,作出理性的决策.
你能说说生活中需要选择方案的例子吗?
宽带网的收费
灯泡的选择
租车方案的选择
旅行社的选择
思考
【例】某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
典型例题
思考
〔1〕影响甲、乙旅行社费用因素是什么?
〔2〕你能用适当的方法表示出甲、乙两个旅行社各需要多少费用吗?
〔3〕在这个问题中有几个变量?自变量和因变量是什么?它们之间是函数关系吗?
人数
甲旅行社:80x元
乙旅行社:(1000+60x)元
自变量是人数,因变量是费用,是函数关系
设该单位参加旅游人数为x,
收费方式
甲旅行社:80x元
乙旅行社:(1000+60x)元
思考
〔4〕如何比较这2种收费方式?
设:选择甲旅行社支付的总费用为y1元,
则y1= 80x
选择乙旅行社支付的总费用为y2元,
则y2= 1000+60x
正比例函数
一次函数
解法一:从“数”上看
当y1=y2 ,即80x=1000+60x时,解得 x=50,
∴当x=50时,选甲或乙旅行社都一样,都是80×50=4000(元);
当y1>y2,即80x>1000+60x时,解得x>50.∴ x>50时,选乙旅行社费用较少;
当y1<y2,即80x<1000+60x时,解得x<50. ∴ x<50时,选甲旅行社费用较少.
思考
〔5〕你能否想出一种直观形象的方法来进行比较呢?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法二:从“形”上看
在同一直角坐标系中作出两个函数的图象
x/人
y/元
y1= 80x
y2= 1000+60x
观察图象,可得:
当人数为50时,选择甲
或乙旅行社费用都一样;
当人数为0~49时,选择
甲旅行社费用较少;
当人数为51~100时,选
择乙旅行社费用较少.
思考
〔6〕你还有其他的方法吗?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法三:作差法①
设选择甲、乙旅行社所需费用之差为y,则y=y1 y2=80x (1000+60x)=20x 1000
一次函数
在平面直角坐标系中作出函数的图象:
x/人
y/元
y= 20x 1000
由图可知:
当x=50时,y=0,即y1=y2,
甲、乙两家旅行社的费用
都一样;
当x>50时,y>0,即y1>y2,
乙旅行社的费用较低;
当x<50时,y<0,即y1<y2,
甲旅行社的费用较低.
y1=y2
思考
〔6〕你还有其他的方法吗?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法三:作差法②
还可以按下面的方法来解:
当80x (1000+60x)=0时,即x=50时,选甲或乙旅行社都一样,
都是80×50=4000(元);
当80x (1000+60x)>0时,即x>50时,选乙旅行社费用较少;
当80x (1000+60x)<0时,即x<50时,选甲旅行社费用较少.
归纳
〔1〕从数学的角度分析数学问题,建立函数模型;
〔2〕列出不等式(方程),求出自变量在取不同值
时所对应的函数值,判断其大小关系;
〔3〕结合实际需求,选择最佳方案.
利用一次函数进行方案决策:
随堂练习
练习1. 某厂日产手套的总成本y元与日产量x副之间的函数表达式为y=5x+40 000,而手套的出厂价格为每副10元,试问该厂至少应日产手套多少副才能不亏本?
解:
根据题意得:
10x (5x+40 000)≥0
解得x≥8000
答:该厂至少应日产手套8000副才能不亏本.
随堂练习
练习2. 某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合同.设汽车每小时行驶xkm,甲公司的月租费是y1元,乙公司的月租费是y2元,y1,y2分别与x之间关系的图象如图所示,观察图象回答:
〔1〕每月行驶的里程在什么范围内,
租乙公司的车合算?
x/km
y/元
y1
y2
1500
解:由图可知:
当0<x<1500时,租乙公司的车
合算.
x/km
y/元
y1
y2
1500
y1=y2
随堂练习
〔2〕每月行驶的里程等于多少时,租两家公司车的费用相同
〔3〕如果这个单位估计每月行驶的里程为2300km,那么这个单位租哪家的车合算?
解:〔2〕由函数图象可知:每月行
驶的里程等于1500km时,租两家车
的费用相同;
〔3〕由函数图象可知:当x>1500时,
y1驶的里程为2300km,那么这个单位
租甲公司出租车合算.
随堂练习
练习3.某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
〔1〕分别求出yA、yB与x之间的函数关系式;
解:yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
随堂练习
解:
〔2〕 ∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少;
〔2〕试讨论A、B两地中,哪个的运费较少;
〔3〕考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
随堂练习
解:
〔3〕设两地运费之和为y元,则
y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
∵y随x的增大而减小,x最大为50,∴y最小=-2×50+9680=9580.
∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B
地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之
和最少,最少是9580元.
〔3〕考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
方案决策
利用一次函数进行方案决策
〔1〕从数学的角度分析数学问题,建立函数模型;
〔2〕列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系;
〔3〕结合实际需求,选择最佳方案.
教科书第54页练习
再见
12.3 一次函数与二元一次方程
第1课时
1.会用等量代换,把二元一次方程转化成一次函数.
2.知道一次函数上的点对应二元一次方程的解.
3.能判断点的坐标是否为二元一次方程的解.
◎重点:二元一次方程和一次函数的相互关系.
◎难点:体会数学中的等价思想.
同学们,还记得等式的性质吗?对于二元一次方程3x+5y=8,能不能将其转化为y=kx+b的形式呢?这就是本节课要学习的一次函数与二元一次方程的关系.
一次函数与二元一次方程的关系
阅读教材本课时所有内容,解决下列问题.
直线上任意一个点的坐标与其所对应的二元一次方程的解有什么关系?
一次函数所在的直线上任意一点的坐标都是其对应的二元一次方程的解.
一次函数与二元一次方程的关系
学法指导:一次函数的一部分可以转化为一元一次方程或一元一次不等式,通过观察一次函数的图象可以得到转化后的方程与不等式的解;而一次函数与其对应的二元一次方程更多的是等价的关系,一次函数上所有的点对应的有序数对(x,y)都是其对应的二元一次方程的解.
1.下列有序实数对中,对应二元一次方程2x+3y=7的解的是( B )
A. (1,2) B.(2,1)
C.(-1,-2) D. (-2,-1)
B
2.已知x=2是方程kx+b=0的解,则一次函数y=kx+b与x轴的交点坐标为( A )
A.(2,0) B.(0,2)
C.(-2,0) D.(0,-2)
3.把二元一次方程2x-y-3=0写成一次函数y= 2x-3 ;把一次函数y=6-2x写成二元一次方程为 2x+y=6 .
A
2x-3
2x+y=6
一次函数与二元一次方程的转化
1.把方程x+1=4y+化为y=kx+b的形式,正确的是
( B )
A.y=x+1 B.y=x+
C.y=x+1 D.y=x+
B
2.方程x+y=4的解有 无数 个,以方程x+y=4的解为坐标的点组成的图象与函数y=-x的图象的位置关系是 平行 .
无数
平行
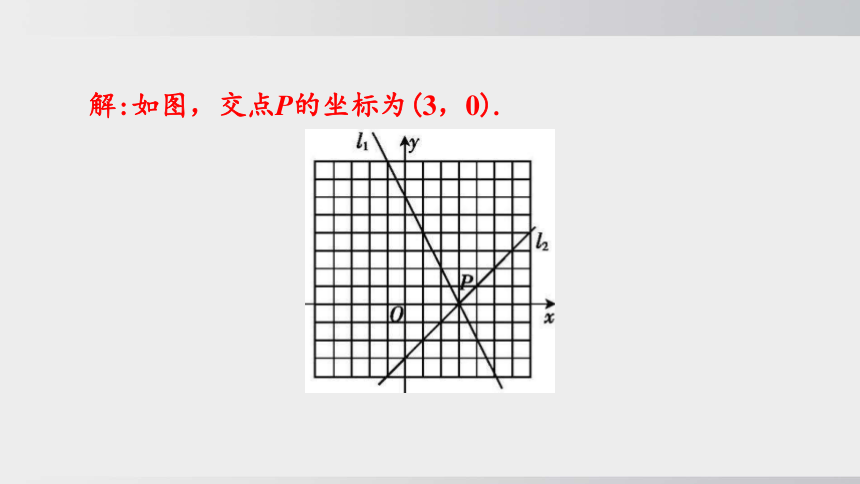
3.在直角坐标系中画出方程2x+y-6=0的图象l1和方程x-y-3=0的图象l2,设l1与l2相交于点P,写出点P的坐标.
解:如图,交点P的坐标为(3,0).
【方法归纳交流】画二元一次方程的图象,其实质就是把二元一次方程化简成一次函数的形式,画出该一次函数的图象即可.
【变式训练】把二元一次方程5x+y-2=0的图象向上平移3个单位后,所得函数解析式是 y=-5x+5 .
y=-5x+5
4.已知二元一次方程3x-y-2=0所在的直线,在平面直角坐标系中与两坐标轴交于两点A、B,O为坐标原点,求三角形AOB的面积.
解:因为3x-y-2=0,所以y=3x-2,所以A、B的坐标为(,0),(0,-2),
所以三角形AOB的面积是××2=.
【变式训练】在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是
( B )
A.(0,) B.(0,)
C.(0,3) D.(0,4)
B
1.已知二元一次方程x+y=3与3x-y=5有一组公共解那么一次函数y=3-x与y=3x-5的图象的交点坐标为
( B )
A.(1,2) B.(2,1)
C.(-1,2) D.(-2,1)
B
2.若函数y=-x+a与y=4x-1的图象交于x轴上一点,求a的值.
解:因为函数y=-x+a与y=4x-1的图象交于x轴上一点,所以令两方程中y=0,即x=a=.
教科书第50页练习
12.3 一次函数与二元一次方程
第2课时
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组.
2.通过一次函数,了解二元一次方程组无解的情形.
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
◎重点:用图象法解二元一次方程组.
◎难点:用函数的观点看待方程,利用函数解决问题.
两条直线可能相交,只有一个交点;可能平行,没有交点;可能重合,有无数个交点.上节课,我们知道一次函数上的点对应二元一次方程的解,那么,两个一次函数的交点坐标对应的是不是两个二元一次方程的公共解呢?
二元一次方程组的图象解法
阅读教材本课时“例1”~“例3”,解决下列问题.
用作图法来解一元二次方程组的步骤是怎样的?
(1)转化形式:把二元一次方程化为一次函数的形式;(2)画函数图象:在同一直角坐标系中画出两个一次函数的图象,并确定交点坐标;(3)写出方程组的解:两条直线的交点坐标就是方程组的解.
1. 一次函数与二元一次方程组的对应关系
二元一次方程组两个一次函数两条直线;
二元一次方程组的解两个一次函数值相等时的自变量值及函数值两条直线的交点坐标.
2. 用图象法求二元一次方程组的解的一般步骤
(1)变函数:把方程组化为一次函数y=k1x+b1与y=k2x+b2;
(2)画图象:建立平面直角坐标系,画出两个一次函数的图象;
(3)找交点:由图象确定两直线交点的坐标;
(4)写结论:依据点的坐标写出方程组的解.
学法指导:利用一次函数的图象求对应的二元一次方程组的解比较麻烦,事实上,我们通常都是利用解二元一次方程组来求两条直线的交点坐标.
二元一次方程组解的情况的判断
阅读教材本课时“思考”中的内容,解决下列问题.
1.明晰概念:一次函数图象(两条直线)位置有三种关系及对应解的情况:
(1)相交(有一个交点) 二元一次方程组有 唯一解 ;
(2)平行(无交点) 二元一次方程组 无解 ;
(3)重合(有无数个交点) 二元一次方程组有 无数个解 .
唯一解
无解
无数个
解
2.直线y1=k1x+b1与直线y2=k2x+b2(k1≠0,k2≠0)不同系数情况下的位置关系.
①k1≠k2 y1与y2相交;
② y1与y2相交于y轴上同一点(0,b1)或(0,b2);
③ y1与y2平行;
④ y1与y2重合.
下面的二元一次方程组中方程无解的是( C )
A. B.
C. D.
C
用图象法解二次一次方程组
1.用图象法解方程组下图中正确的是( C )
A B
C
C D
【变式训练】用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图),则所解的二元一次方程组是( D )
D
A. B.
C. D.
2.如图,函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的的二元一次方程组的解是 .
利用方程组求两直线交点
3.求直线y=2x+4与y=-x+1的交点坐标.
解:由题意,得方程组
解这个方程组,得即交点坐标为(-1,2).
【方法归纳交流】在利用解方程组求两条直线y=k1x+b1和y=k2x+b2的交点坐标时,可直接消去y,得到k1x+b1=k2x+b2.在求得的解中,自变量的值作为横坐标,函数值作为纵坐标,要防止坐标顺序错误.
【变式训练】有两条直线y=ax+b和y=cx+5,学生甲求得它们的交点坐标为(3,-2),学生乙因看错c而求得它们的交点为(4,5),求两条直线的表达式.
解:把(3,-2)代入y=cx+5,得c=-.由点(4,5)和点(3,-2)都在函数y=ax+b上,所以有解得a=7,b=-23.所求的函数表达式为y=7x-23和y=-x+5.
两直线的位置关系与方程组的解
4.一次函数y=2x-1与y=2x+3的图象是两条 平行 (填“相交”或“平行”)的直线,因此方程组的解的情况是 无解 .
平行
无解
【变式训练】无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在( C )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
二元一次方程组的解与两直线l1:a1x+b1y=c1与l2:a2x+b2y=c2位置关系的联系(其中6 个常数均不为零):
从“数”看 从“形”看
≠ 方程组有唯一解 l1与l2相交
= ≠ 方程组无解 l1与l2平行
== 方程组有无数个解 l1与l2重合
1.当k>时,直线kx-y=k与直线ky+x=2k的交点在
( A )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
2.如图,直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P.求三角形APB的面积.
解:由题意得方程组
解得
所以点P坐标为(-1,-1),
所以S三角形ABP==.
教科书第52页练习
12.3 一次函数与二元一次方程
第3课时
学习目标
1.深入了解一次函数的应用价值.
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.
3.从问题的解决与探究中进一步感悟函数的应用价值,培养解决实际问题的数学能力.
4.通过从实际问题中得到函数关系式这一过程,提升学生的数学应用能力,使学生在探索过程中体验成功的喜悦,树立学习的自信心.
方案决策
情境引入
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清晰地认识各种方案,作出理性的决策.
你能说说生活中需要选择方案的例子吗?
宽带网的收费
灯泡的选择
租车方案的选择
旅行社的选择
思考
【例】某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
典型例题
思考
〔1〕影响甲、乙旅行社费用因素是什么?
〔2〕你能用适当的方法表示出甲、乙两个旅行社各需要多少费用吗?
〔3〕在这个问题中有几个变量?自变量和因变量是什么?它们之间是函数关系吗?
人数
甲旅行社:80x元
乙旅行社:(1000+60x)元
自变量是人数,因变量是费用,是函数关系
设该单位参加旅游人数为x,
收费方式
甲旅行社:80x元
乙旅行社:(1000+60x)元
思考
〔4〕如何比较这2种收费方式?
设:选择甲旅行社支付的总费用为y1元,
则y1= 80x
选择乙旅行社支付的总费用为y2元,
则y2= 1000+60x
正比例函数
一次函数
解法一:从“数”上看
当y1=y2 ,即80x=1000+60x时,解得 x=50,
∴当x=50时,选甲或乙旅行社都一样,都是80×50=4000(元);
当y1>y2,即80x>1000+60x时,解得x>50.∴ x>50时,选乙旅行社费用较少;
当y1<y2,即80x<1000+60x时,解得x<50. ∴ x<50时,选甲旅行社费用较少.
思考
〔5〕你能否想出一种直观形象的方法来进行比较呢?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法二:从“形”上看
在同一直角坐标系中作出两个函数的图象
x/人
y/元
y1= 80x
y2= 1000+60x
观察图象,可得:
当人数为50时,选择甲
或乙旅行社费用都一样;
当人数为0~49时,选择
甲旅行社费用较少;
当人数为51~100时,选
择乙旅行社费用较少.
思考
〔6〕你还有其他的方法吗?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法三:作差法①
设选择甲、乙旅行社所需费用之差为y,则y=y1 y2=80x (1000+60x)=20x 1000
一次函数
在平面直角坐标系中作出函数的图象:
x/人
y/元
y= 20x 1000
由图可知:
当x=50时,y=0,即y1=y2,
甲、乙两家旅行社的费用
都一样;
当x>50时,y>0,即y1>y2,
乙旅行社的费用较低;
当x<50时,y<0,即y1<y2,
甲旅行社的费用较低.
y1=y2
思考
〔6〕你还有其他的方法吗?
收费方式
甲旅行社: y1= 80x
乙旅行社:y2= 1000+60x
解法三:作差法②
还可以按下面的方法来解:
当80x (1000+60x)=0时,即x=50时,选甲或乙旅行社都一样,
都是80×50=4000(元);
当80x (1000+60x)>0时,即x>50时,选乙旅行社费用较少;
当80x (1000+60x)<0时,即x<50时,选甲旅行社费用较少.
归纳
〔1〕从数学的角度分析数学问题,建立函数模型;
〔2〕列出不等式(方程),求出自变量在取不同值
时所对应的函数值,判断其大小关系;
〔3〕结合实际需求,选择最佳方案.
利用一次函数进行方案决策:
随堂练习
练习1. 某厂日产手套的总成本y元与日产量x副之间的函数表达式为y=5x+40 000,而手套的出厂价格为每副10元,试问该厂至少应日产手套多少副才能不亏本?
解:
根据题意得:
10x (5x+40 000)≥0
解得x≥8000
答:该厂至少应日产手套8000副才能不亏本.
随堂练习
练习2. 某单位急需用车,他们准备和甲、乙两个出租车公司签订月租车合同.设汽车每小时行驶xkm,甲公司的月租费是y1元,乙公司的月租费是y2元,y1,y2分别与x之间关系的图象如图所示,观察图象回答:
〔1〕每月行驶的里程在什么范围内,
租乙公司的车合算?
x/km
y/元
y1
y2
1500
解:由图可知:
当0<x<1500时,租乙公司的车
合算.
x/km
y/元
y1
y2
1500
y1=y2
随堂练习
〔2〕每月行驶的里程等于多少时,租两家公司车的费用相同
〔3〕如果这个单位估计每月行驶的里程为2300km,那么这个单位租哪家的车合算?
解:〔2〕由函数图象可知:每月行
驶的里程等于1500km时,租两家车
的费用相同;
〔3〕由函数图象可知:当x>1500时,
y1
租甲公司出租车合算.
随堂练习
练习3.某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
〔1〕分别求出yA、yB与x之间的函数关系式;
解:yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
随堂练习
解:
〔2〕 ∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少;
〔2〕试讨论A、B两地中,哪个的运费较少;
〔3〕考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
随堂练习
解:
〔3〕设两地运费之和为y元,则
y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
∵y随x的增大而减小,x最大为50,∴y最小=-2×50+9680=9580.
∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B
地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之
和最少,最少是9580元.
〔3〕考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
方案决策
利用一次函数进行方案决策
〔1〕从数学的角度分析数学问题,建立函数模型;
〔2〕列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系;
〔3〕结合实际需求,选择最佳方案.
教科书第54页练习
再见
