13.1 三角形中的边角关系(共59张PPT)2025年秋沪科版八年级数学上册
文档属性
| 名称 | 13.1 三角形中的边角关系(共59张PPT)2025年秋沪科版八年级数学上册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 09:37:54 | ||
图片预览





文档简介
(共59张PPT)
13.1 三角形中的边角关系
1.三角形中边的关系
学习目标
三角形中边的关系
准备好了吗?一起去探索吧!
1.理解三角形概念及其基本要素.
2.证明三角形两边的和大于第三边,并能运用它解决有关问题.
3.经历探索三角形三边关系的过程,培养学生的分类讨论的思想;运用几何语言有条理的表达能力,体会三角形知识的应用价值.
4.认识到通过观察、比较、推断获得解决实际问题的方法,使学生体会到数学源于生活,而又在生活实践探索中得到解决.
情境引入
观察这些实物,里边有你熟悉的几何图形吗?
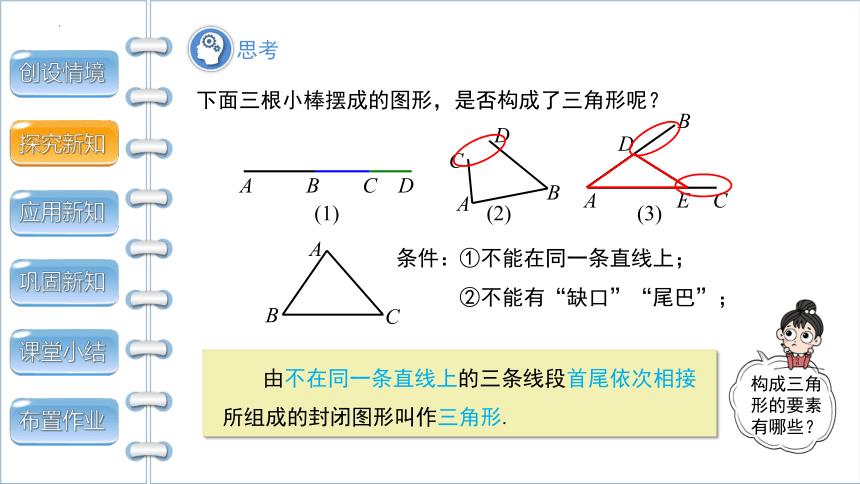
下面三根小棒摆成的图形,是否构成了三角形呢?
思考
C
A
B
D
B
A
C
(3)
A B C D
(1)
(2)
条件:
D
E
A
B
C
①不能在同一条直线上;
②不能有“缺口”“尾巴”;
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫作三角形.
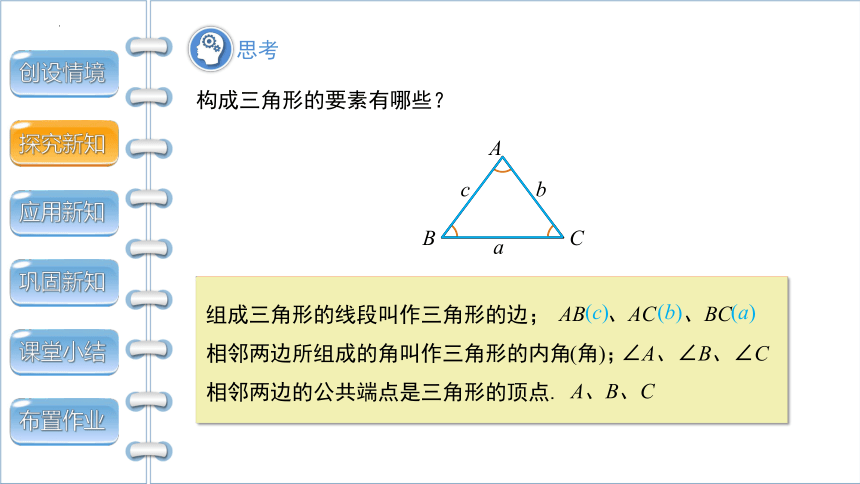
构成三角形的要素有哪些?
构成三角形的要素有哪些?
组成三角形的线段叫作三角形的边;
相邻两边所组成的角叫作三角形的内角
相邻两边的公共端点是三角形的顶点.
AB 、AC 、BC
(c) (b) (a)
(角);
A
B
C
a
b
c
A、B、C
∠A、∠B、∠C
思考
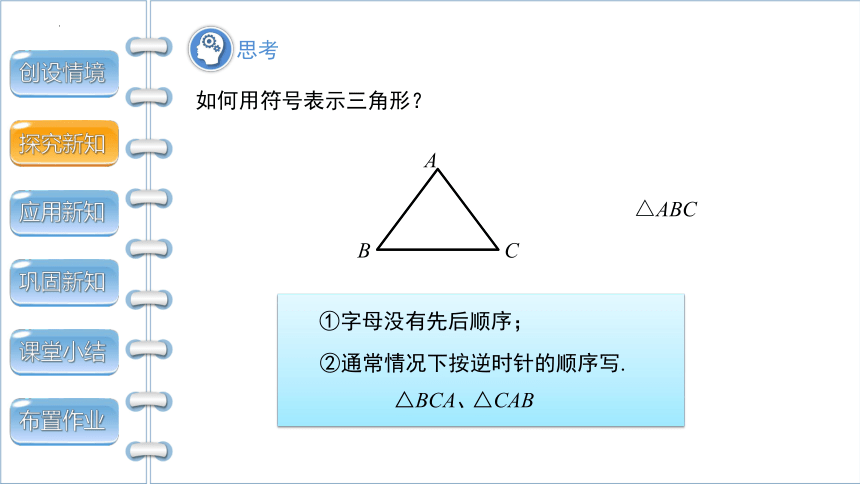
如何用符号表示三角形?
A
B
C
ABC
△
①字母没有先后顺序;
②通常情况下按逆时针的顺序写.
△BCA、
△CAB
思考
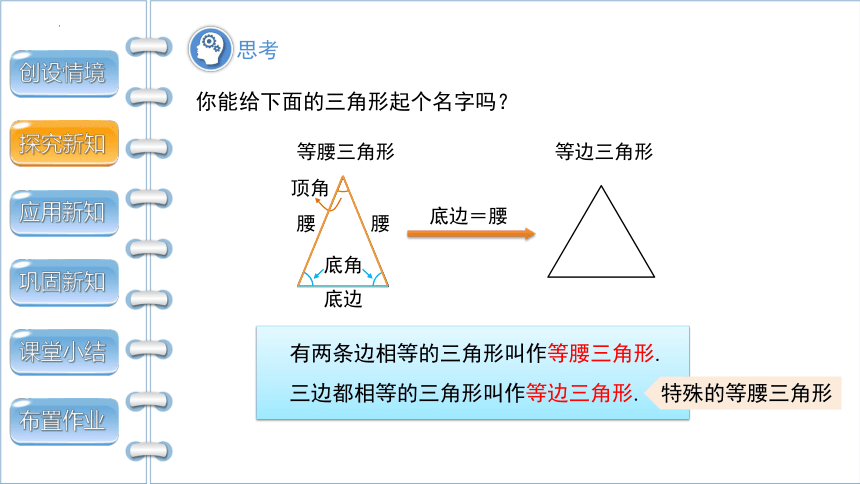
等腰三角形
等边三角形
有两条边相等的三角形叫作等腰三角形.
腰
腰
底边
底角
顶角
三边都相等的三角形叫作等边三角形.
底边=腰
你能给下面的三角形起个名字吗?
思考
特殊的等腰三角形
思考
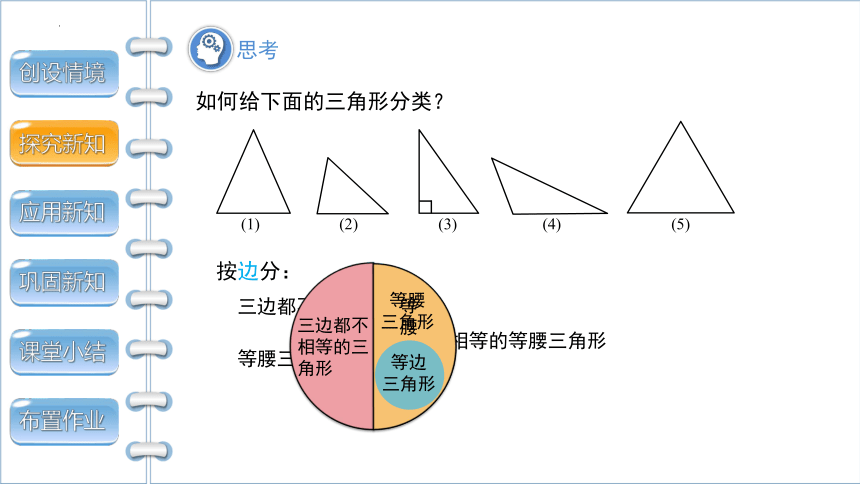
如何给下面的三角形分类?
按边分:
三边都不相等的三角形
底边和腰不相等的等腰三角形
等边三角形
等腰三角形
三边都不相等的三角形
等腰三角形
等边
三角形
等腰
三角形
(1)
(2)
(3)
(4)
(5)
思考
设置三组小棒的长度,让学生动手操作,看能否拼成三角形
第一组:3cm,4cm,5cm(能拼成三角形)
第二组:2cm,3cm,5cm(在一条直线上,不能拼成三角形)
第三组:1cm,2cm,8cm(不能拼成三角形)
在一个三角形中,任意两边之和与第三边的大小关系如何?你判断的依据是什么?
思考
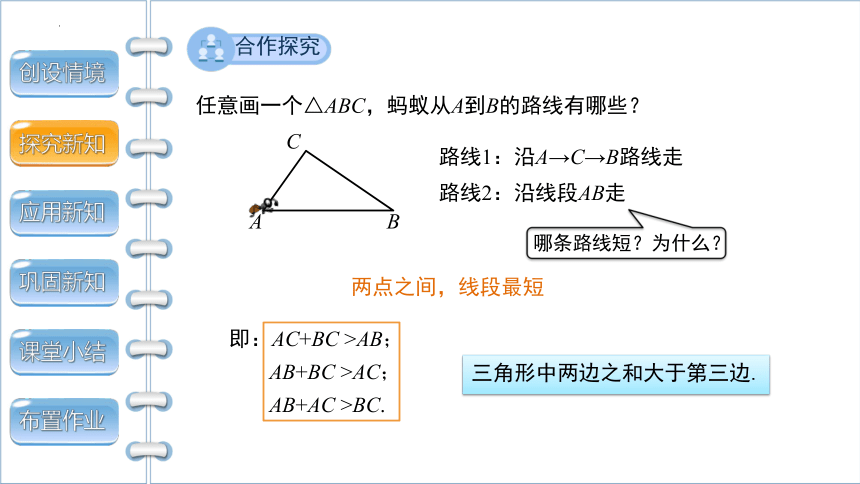
任意画一个△ABC,蚂蚁从A到B的路线有哪些?
C
A
B
路线1:沿A→C→B路线走
哪条路线短?为什么?
路线2:沿线段AB走
即:AC+BC >AB;
AB+BC >AC;
AB+AC >BC.
三角形中两边之和大于第三边.
两点之间,线段最短
合作探究
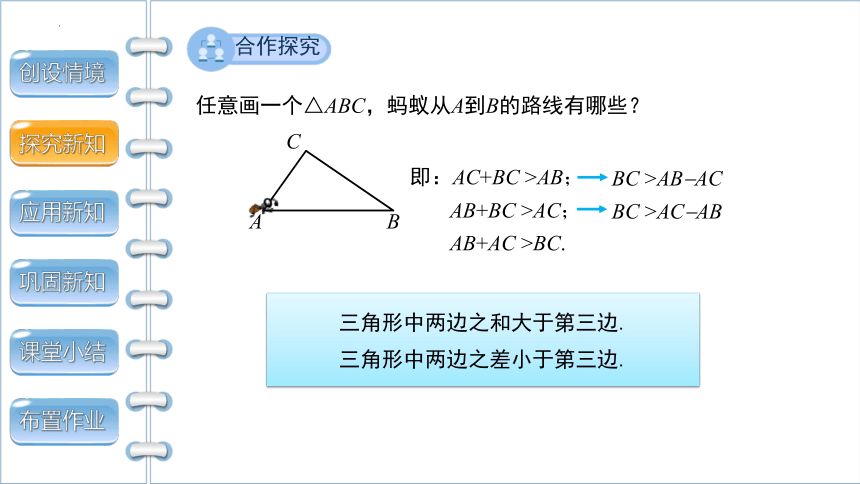
任意画一个△ABC,蚂蚁从A到B的路线有哪些?
C
A
B
合作探究
即:AC+BC >AB;
AB+BC >AC;
AB+AC >BC.
BC >AB AC
BC >AC AB
三角形中两边之和大于第三边.
三角形中两边之差小于第三边.
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
有没有更简便的判断方法?
做一做
只要满足较短的两条线段之和大于最长线段,便可构成三角形; 否则不能组成三角形.
典型例题
(1)如果腰长是底边长的2倍,求各边长;
解:设等腰三角形的底边长为xcm,则腰长为2xcm.
根据题意,得 x+2x+2x=18.
解方程,得x=3.6.
所以三角形的三边长为3.6cm,7.2cm,7.2cm.
例1 等腰三角形中,周长为18cm.
x
2x
2x
典型例题
(2)如果一边的长为4cm,求另两边长.
例1 等腰三角形中,周长为18cm.
是底还是腰?
分类讨论
解:若底边长为4cm,设腰长为xcm.
根据题意,得 2x+4=18.解方程,得 x =7;
若腰长为4cm,设底边长为xcm.
根据题意,得 2 4+ x =18.解方程,得 x =10.
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形.
所以,三角形的另两边长都是7cm.
典型例题
例2 在△ABC中,AC=5,BC=2,求△ABC周长L的取值范围.
关键:第三边
5
2
C
A
B
解:∵ AC+BC>AB,∴AB<7
∵ AC BC3
可得:3∵△ABC的周长L=AC+BC+AB=AB+7
∴ L的取值范围是:10第三边的取值范围:
两边之差<第三边<两边之和
抢答
随堂练习
1.说出图中的各个三角形.并表示出来.并说一说每个三角形的边、顶点、角.
A
D
B
E
C
△ABE
△BCE
△CDE
△ABC
△BCD
2.上图中,以BC为边的三角形有哪些?
△BCE
△ABC
△BCD
抢答
随堂练习
3.已知等腰三角形的一边长为5cm,一边长为6cm,求它的周长.
①如果底边长为5cm,腰长为6cm,
此时三边长分别为:5,6,6,满足:5+6>6,能够成三角形.
三角形的周长L=5+6+6=17(cm);
②如果底边长为6cm,腰长为5cm,
此时三边长分别为:5,5,6, 满足:5+5>6,能够成三角形;
三角形的周长L=5+5+6=16(cm).
综上,该等腰三角形的周长为16cm或17cm.
解:
抢答
随堂练习
解:∵ AC BC可得:3∵AB为奇数,
∴ AB=5.
∴ △ABC的周长L=3+5+7=15.
4. 在△ABC中,AC=5,BC=2,且AB为奇数,求△ABC周长L.
三角形中边的关系
三角形的定义:
三角形的分类(按边分):
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫作三角形.
三边关系:
三角形中两边之和大于第三边.
三角形中两边之差小于第三边.
教科书第66页练习
13.1 三角形中的边角关系
2.三角形中角的关系
学习目标
三角形中角的关系
准备好了吗?一起去探索吧!
1.探索并掌握三角形内角和定理.
2.会用三角形内角和进行角度的计算.
3.能运用三角形的内角和定理及其推论判断角和边的关系,解决简单的实际问题.
4.通过探究三角形角的数量关系,引起学生的好奇心,激发学生的求知欲,并发展学生的合情推理能力,养成独立思考的习惯.
情景引入
在一个直角三角形里住着三个内角,平时它们三兄弟非常团结.
可是,有一天,二哥突然不高兴了,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”
大哥说:“不行啊!否则,我们这个家就围不起来了……”.
老大
老二
老三
你能帮着“大哥”解释一下吗?
有一个角是钝角的三角形叫作钝角三角形.
有一个角是直角的三角形叫作直角三角形.
三角形按照角的大小分类,怎样分?
锐角三角形
直角三角形
钝角三角形
三个角都是锐角的三角形叫作锐角三角形.
斜
三
角
形
直角三角形
思考
直角三角形中夹直角的两边叫作直角边,
直角相对的边叫作斜边,
直角三角形ABC可以写成“Rt△ABC”.
三角形按照角分类,怎样分?
思考
钝角三角形
直角三角形
锐角三角形
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
在一个三角形中,三个内角之间有什么关系?
思考
在一个三角形中,三个内角之间有什么关系?
折叠法
剪拼图、折叠、度量
2
3
1
3
1
2
三角形的内角和等于180°
∠1+∠2+∠3=180°
思考
剪拼法
剪拼图、折叠、度量
在一个三角形中,三个内角之间有什么关系?
三角形的内角和等于180°
三个内角的和仍然是180°
归纳总结
同一个三角形中三个内角的关系
三角形的内角和等于180°.
A
B
C
A
B
C
A
B
C
∠A+∠B+∠C=180°
任意三角形
思考
你现在能解释这个问题了吗?
在一个直角三角形里住着三个内角,平时它们三兄弟非常团结.
可是,有一天,二哥突然不高兴了,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”
大哥说:“不行啊!否则,我们这个家就围不起来了……”.
老大
老二
老三
三角形的内角和等于180°.
如图,说出各图中∠1 的度数.
80°
50°
1
105°
30°
1
22°
1
(1)
(2)
(3)
做一做
∠1=50°
∠1=45°
∠1=68°
三角形的内角和等于180°.
典型例题
例 已知:如下图,△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A和∠C的度数.
B
A
C
D
解析:可以从以下三个方面考虑,
①所求的角在哪个三角形内;
②所在三角形内其它两个角的度数;
③根据“三角形的内角和等于180°”进行求解计算.
典型例题
B
A
C
D
54°
18°
解:因为BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+∠ABD+∠ADB=180°,(三角形的内角和等于180°)
∠ABD=54°,∠ADB=90°,(已知)
∠A=180°–∠ABD–∠ADB
=180°–54°–90°=36°.
90°
在△ABC中,
∠C=180°–∠A–(∠ABD+∠DBC)
=180°–36°–(54°+18°)=72°.
36°
例 已知:如下图,△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A和∠C的度数.
抢答
随堂练习
1. 在△ABC中:
(1)已知:∠A=105°,∠B–∠C=15°,则∠C= ;
(2)已知:∠A∶∠B∶∠C=3∶4∶5,则∠C= .
30°
75°
三角形的内角和等于180°.
D
抢答
随堂练习
2. 已知:如图,∠ACB=90°,CD⊥AB,垂足是D.
(1)写出图中所有相等的角;
(2)写出图中所有直角三角形,并指出它们的斜边.
解:(1) ∠ACB=∠ADC=∠CDB,
∠CAB=∠DCB,
B
A
C
∠ACD=∠B.
(2) Rt△ACB,
Rt△CDB,
Rt△ADC,
AB是斜边;
CB是斜边;
AC是斜边.
抢答
随堂练习
3. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC
=46°.求∠CAD的度数.
B
A
C
D
解:在△ABC中,
∠B=70°,∠BAC=46°,
所有∠C=180°–70°–46°=64°.
在Rt△ADC,
∠C=64°,∠ADC=90°,
所有∠CAD=180°–64°–90°=26°.
三角形中角的关系
三角形按角的大小分类:
三角形三个内角的关系:
三角形的内角和等于180°.
任意三角形
教科书第68页练习
13.1 三角形中的边角关系
3.三角形中几条重要线段
学习目标
三角形中几条重要的线段
准备好了吗?一起去探索吧!
1.理解三角形的高、中线与角平分线的概念,了解定义、三角形的重心的概念.
2.能正确作出一个三角形的高线、中线、角平分线,并掌握相关性质.
3.经历画图、观察、操作、描述等实践过程,加深对知识的理解,感受数学语言的准确性,提高学生的观察能力、归纳总结能力等.
4.通过教学活动,让学生感受数学的严谨性,图形中蕴含的规律性,激发学生的学习兴趣和求知欲望,使学生乐于探究、敢于探究.
l
A
B
如何利用直尺和三角板,过直线外一点作这条直线的垂线
画
放
移
靠
过三角形的一个顶点,你能画出它的对边的垂线吗
思考
回顾
思考
A
B
C
D
三角形的高线
从三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,也叫作三角形的高.
注意:标明垂直的记号和垂足的字母.
符号语言:
∵在△ABC中, AD⊥BC,
∴∠ADB ∠ADC 90°.
你还能画出三角形其它边上的高吗?
操作
A
B
C
D
E
F
试着作出△ABC的另外两条高.
观察图形,你发现了什么?
1.锐角三角形的三条高都在三角形的内部.
2.锐角三角形的三条高交于一点.
这个结论对所有的三角形都成立吗?
操作
讨论
几条高?在三角形内部还是外部?有没有交点……
A
B
C
D
E
F
试着作出直角三角形、钝角三角形的三条高.
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
钝角三角形
E
F
归纳
钝角三角形
A
B
C
D
E
F
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
E
F
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
归纳
相同点:三角形三条高所在的直线交于一点.
不同点:
锐角三角形三条高的交点在三角形的内部;
直角三角形三条高的交点在直角顶点;
钝角三角形三条高的交点在三角形的外部.
思考
你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
A
B
C
三角形的中线:
三角形中,连接一个顶点与它对边中点的线段叫作三角形的中线.
D
E
F
符号语言:
∵AD是△ABC的BC边的中线,
∴BD DC BC.
操作
任意画一个三角形,画出它的所有中线,它们有什么特点?
A
B
C
D
E
F
A
B
C
锐角三角形
直角三角形
A
B
C
钝角三角形
(1)任何三角形有三条中线,并且都在三角形的内部,交于一点;
● 三角形的中线的特征:
(2)三角形的中线是一条线段;
(3)三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.
归纳
A
B
C
D
E
F
三角形的重心:
三角形三条中线的交点叫作三角形的重心.
O
思考
C
A
B
准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕AD把∠ABC分成∠1和∠2两个角.∠1和∠2有什么关系?
C
A
B
C
A
B
D
C'
1
2
三角形的角平分线:
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫作三角形的角平分线.
符号语言:∵AD是△ABC的∠BAC的平分线,∴∠1 ∠2 ∠BAC.
操作
任意画一个三角形,画出它的所有角平分线,它们有什么特点?
C
A
B
D
F
F
A
B
C
C
B
A
锐角三角形
直角三角形
钝角三角形
三角形的三条角平分线在三角形的内部交于一点.
归纳
三角形的高
三角形的
中线
三角形的
角平分线
图形
特点
数量
3
3
3
位置
三条高所在的直线交于一点
在三角形内部、外部、三角形上
三条中线在三角形内部交于一点
三条角平分线在三角形内部交于一点
典型例题
例1 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC 60°,∠BCE 40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC 60°,
∴∠DAC ∠BAD 30°.
∵CE是△ABC的高,∠BCE 40°,
∴∠B 50°.
∴∠ADB 180° ∠B ∠BAD
180° 30° 50° 100°.
A
B
C
D
E
30°
40°
典型例题
例2 在△ABC中,CD是中线,已知BC AC 5cm,△DBC的周长为25cm,求△ADC的周长.
解:∵CD是△ABC的中线,
∴BD AD.
又∵BC AC 5cm,
△DBC的周长 BC BD CD 25cm,
∴△ADC的周长 AD CD AC
BD CD BC 5
25 5
20(cm).
A
D
B
C
AC (BC 5) cm
抢答
随堂练习
1.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
A
B
C
D
分析:
锐角三角形三条高的交点在三角形的内部;
直角三角形三条高的交点在直角顶点;
钝角三角形三条高的交点在三角形的外部.
抢答
随堂练习
2. 三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
分析:
三角形一边上的中线,把原三角形分成底相等、高相同的两个三角形,两个三角形等底同高则面积相等.
B
A
B
C
D
抢答
随堂练习
3.如图,在△ABC中,∠BAC 60°,∠B 45°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
解:∵AD是△ABC的角平分线,∠BAC 60°,
∴∠BAD ∠DAC 30°.
∵ 在△ABD中,∠B ∠ADB ∠BAD 180°,
∴∠ADB 180° ∠B ∠BAD
180° 45° 30° 105°.
三角形中几条重要的线段
三角形的几条重要线段:
高线:从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,也叫做三角形的高.
中线:三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
角平分线:三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
教科书第70页练习
13.1 三角形中的边角关系
1.三角形中边的关系
学习目标
三角形中边的关系
准备好了吗?一起去探索吧!
1.理解三角形概念及其基本要素.
2.证明三角形两边的和大于第三边,并能运用它解决有关问题.
3.经历探索三角形三边关系的过程,培养学生的分类讨论的思想;运用几何语言有条理的表达能力,体会三角形知识的应用价值.
4.认识到通过观察、比较、推断获得解决实际问题的方法,使学生体会到数学源于生活,而又在生活实践探索中得到解决.
情境引入
观察这些实物,里边有你熟悉的几何图形吗?
下面三根小棒摆成的图形,是否构成了三角形呢?
思考
C
A
B
D
B
A
C
(3)
A B C D
(1)
(2)
条件:
D
E
A
B
C
①不能在同一条直线上;
②不能有“缺口”“尾巴”;
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫作三角形.
构成三角形的要素有哪些?
构成三角形的要素有哪些?
组成三角形的线段叫作三角形的边;
相邻两边所组成的角叫作三角形的内角
相邻两边的公共端点是三角形的顶点.
AB 、AC 、BC
(c) (b) (a)
(角);
A
B
C
a
b
c
A、B、C
∠A、∠B、∠C
思考
如何用符号表示三角形?
A
B
C
ABC
△
①字母没有先后顺序;
②通常情况下按逆时针的顺序写.
△BCA、
△CAB
思考
等腰三角形
等边三角形
有两条边相等的三角形叫作等腰三角形.
腰
腰
底边
底角
顶角
三边都相等的三角形叫作等边三角形.
底边=腰
你能给下面的三角形起个名字吗?
思考
特殊的等腰三角形
思考
如何给下面的三角形分类?
按边分:
三边都不相等的三角形
底边和腰不相等的等腰三角形
等边三角形
等腰三角形
三边都不相等的三角形
等腰三角形
等边
三角形
等腰
三角形
(1)
(2)
(3)
(4)
(5)
思考
设置三组小棒的长度,让学生动手操作,看能否拼成三角形
第一组:3cm,4cm,5cm(能拼成三角形)
第二组:2cm,3cm,5cm(在一条直线上,不能拼成三角形)
第三组:1cm,2cm,8cm(不能拼成三角形)
在一个三角形中,任意两边之和与第三边的大小关系如何?你判断的依据是什么?
思考
任意画一个△ABC,蚂蚁从A到B的路线有哪些?
C
A
B
路线1:沿A→C→B路线走
哪条路线短?为什么?
路线2:沿线段AB走
即:AC+BC >AB;
AB+BC >AC;
AB+AC >BC.
三角形中两边之和大于第三边.
两点之间,线段最短
合作探究
任意画一个△ABC,蚂蚁从A到B的路线有哪些?
C
A
B
合作探究
即:AC+BC >AB;
AB+BC >AC;
AB+AC >BC.
BC >AB AC
BC >AC AB
三角形中两边之和大于第三边.
三角形中两边之差小于第三边.
下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
有没有更简便的判断方法?
做一做
只要满足较短的两条线段之和大于最长线段,便可构成三角形; 否则不能组成三角形.
典型例题
(1)如果腰长是底边长的2倍,求各边长;
解:设等腰三角形的底边长为xcm,则腰长为2xcm.
根据题意,得 x+2x+2x=18.
解方程,得x=3.6.
所以三角形的三边长为3.6cm,7.2cm,7.2cm.
例1 等腰三角形中,周长为18cm.
x
2x
2x
典型例题
(2)如果一边的长为4cm,求另两边长.
例1 等腰三角形中,周长为18cm.
是底还是腰?
分类讨论
解:若底边长为4cm,设腰长为xcm.
根据题意,得 2x+4=18.解方程,得 x =7;
若腰长为4cm,设底边长为xcm.
根据题意,得 2 4+ x =18.解方程,得 x =10.
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形.
所以,三角形的另两边长都是7cm.
典型例题
例2 在△ABC中,AC=5,BC=2,求△ABC周长L的取值范围.
关键:第三边
5
2
C
A
B
解:∵ AC+BC>AB,∴AB<7
∵ AC BC
可得:3
∴ L的取值范围是:10
两边之差<第三边<两边之和
抢答
随堂练习
1.说出图中的各个三角形.并表示出来.并说一说每个三角形的边、顶点、角.
A
D
B
E
C
△ABE
△BCE
△CDE
△ABC
△BCD
2.上图中,以BC为边的三角形有哪些?
△BCE
△ABC
△BCD
抢答
随堂练习
3.已知等腰三角形的一边长为5cm,一边长为6cm,求它的周长.
①如果底边长为5cm,腰长为6cm,
此时三边长分别为:5,6,6,满足:5+6>6,能够成三角形.
三角形的周长L=5+6+6=17(cm);
②如果底边长为6cm,腰长为5cm,
此时三边长分别为:5,5,6, 满足:5+5>6,能够成三角形;
三角形的周长L=5+5+6=16(cm).
综上,该等腰三角形的周长为16cm或17cm.
解:
抢答
随堂练习
解:∵ AC BC
∴ AB=5.
∴ △ABC的周长L=3+5+7=15.
4. 在△ABC中,AC=5,BC=2,且AB为奇数,求△ABC周长L.
三角形中边的关系
三角形的定义:
三角形的分类(按边分):
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫作三角形.
三边关系:
三角形中两边之和大于第三边.
三角形中两边之差小于第三边.
教科书第66页练习
13.1 三角形中的边角关系
2.三角形中角的关系
学习目标
三角形中角的关系
准备好了吗?一起去探索吧!
1.探索并掌握三角形内角和定理.
2.会用三角形内角和进行角度的计算.
3.能运用三角形的内角和定理及其推论判断角和边的关系,解决简单的实际问题.
4.通过探究三角形角的数量关系,引起学生的好奇心,激发学生的求知欲,并发展学生的合情推理能力,养成独立思考的习惯.
情景引入
在一个直角三角形里住着三个内角,平时它们三兄弟非常团结.
可是,有一天,二哥突然不高兴了,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”
大哥说:“不行啊!否则,我们这个家就围不起来了……”.
老大
老二
老三
你能帮着“大哥”解释一下吗?
有一个角是钝角的三角形叫作钝角三角形.
有一个角是直角的三角形叫作直角三角形.
三角形按照角的大小分类,怎样分?
锐角三角形
直角三角形
钝角三角形
三个角都是锐角的三角形叫作锐角三角形.
斜
三
角
形
直角三角形
思考
直角三角形中夹直角的两边叫作直角边,
直角相对的边叫作斜边,
直角三角形ABC可以写成“Rt△ABC”.
三角形按照角分类,怎样分?
思考
钝角三角形
直角三角形
锐角三角形
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
在一个三角形中,三个内角之间有什么关系?
思考
在一个三角形中,三个内角之间有什么关系?
折叠法
剪拼图、折叠、度量
2
3
1
3
1
2
三角形的内角和等于180°
∠1+∠2+∠3=180°
思考
剪拼法
剪拼图、折叠、度量
在一个三角形中,三个内角之间有什么关系?
三角形的内角和等于180°
三个内角的和仍然是180°
归纳总结
同一个三角形中三个内角的关系
三角形的内角和等于180°.
A
B
C
A
B
C
A
B
C
∠A+∠B+∠C=180°
任意三角形
思考
你现在能解释这个问题了吗?
在一个直角三角形里住着三个内角,平时它们三兄弟非常团结.
可是,有一天,二哥突然不高兴了,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”
大哥说:“不行啊!否则,我们这个家就围不起来了……”.
老大
老二
老三
三角形的内角和等于180°.
如图,说出各图中∠1 的度数.
80°
50°
1
105°
30°
1
22°
1
(1)
(2)
(3)
做一做
∠1=50°
∠1=45°
∠1=68°
三角形的内角和等于180°.
典型例题
例 已知:如下图,△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A和∠C的度数.
B
A
C
D
解析:可以从以下三个方面考虑,
①所求的角在哪个三角形内;
②所在三角形内其它两个角的度数;
③根据“三角形的内角和等于180°”进行求解计算.
典型例题
B
A
C
D
54°
18°
解:因为BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+∠ABD+∠ADB=180°,(三角形的内角和等于180°)
∠ABD=54°,∠ADB=90°,(已知)
∠A=180°–∠ABD–∠ADB
=180°–54°–90°=36°.
90°
在△ABC中,
∠C=180°–∠A–(∠ABD+∠DBC)
=180°–36°–(54°+18°)=72°.
36°
例 已知:如下图,△ABC中,BD⊥AC,垂足为D.∠ABD=54°,∠DBC=18°.求∠A和∠C的度数.
抢答
随堂练习
1. 在△ABC中:
(1)已知:∠A=105°,∠B–∠C=15°,则∠C= ;
(2)已知:∠A∶∠B∶∠C=3∶4∶5,则∠C= .
30°
75°
三角形的内角和等于180°.
D
抢答
随堂练习
2. 已知:如图,∠ACB=90°,CD⊥AB,垂足是D.
(1)写出图中所有相等的角;
(2)写出图中所有直角三角形,并指出它们的斜边.
解:(1) ∠ACB=∠ADC=∠CDB,
∠CAB=∠DCB,
B
A
C
∠ACD=∠B.
(2) Rt△ACB,
Rt△CDB,
Rt△ADC,
AB是斜边;
CB是斜边;
AC是斜边.
抢答
随堂练习
3. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC
=46°.求∠CAD的度数.
B
A
C
D
解:在△ABC中,
∠B=70°,∠BAC=46°,
所有∠C=180°–70°–46°=64°.
在Rt△ADC,
∠C=64°,∠ADC=90°,
所有∠CAD=180°–64°–90°=26°.
三角形中角的关系
三角形按角的大小分类:
三角形三个内角的关系:
三角形的内角和等于180°.
任意三角形
教科书第68页练习
13.1 三角形中的边角关系
3.三角形中几条重要线段
学习目标
三角形中几条重要的线段
准备好了吗?一起去探索吧!
1.理解三角形的高、中线与角平分线的概念,了解定义、三角形的重心的概念.
2.能正确作出一个三角形的高线、中线、角平分线,并掌握相关性质.
3.经历画图、观察、操作、描述等实践过程,加深对知识的理解,感受数学语言的准确性,提高学生的观察能力、归纳总结能力等.
4.通过教学活动,让学生感受数学的严谨性,图形中蕴含的规律性,激发学生的学习兴趣和求知欲望,使学生乐于探究、敢于探究.
l
A
B
如何利用直尺和三角板,过直线外一点作这条直线的垂线
画
放
移
靠
过三角形的一个顶点,你能画出它的对边的垂线吗
思考
回顾
思考
A
B
C
D
三角形的高线
从三角形的一个顶点到它对边所在直线的垂线段叫作三角形的高线,也叫作三角形的高.
注意:标明垂直的记号和垂足的字母.
符号语言:
∵在△ABC中, AD⊥BC,
∴∠ADB ∠ADC 90°.
你还能画出三角形其它边上的高吗?
操作
A
B
C
D
E
F
试着作出△ABC的另外两条高.
观察图形,你发现了什么?
1.锐角三角形的三条高都在三角形的内部.
2.锐角三角形的三条高交于一点.
这个结论对所有的三角形都成立吗?
操作
讨论
几条高?在三角形内部还是外部?有没有交点……
A
B
C
D
E
F
试着作出直角三角形、钝角三角形的三条高.
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
钝角三角形
E
F
归纳
钝角三角形
A
B
C
D
E
F
A
B
C
D
锐角三角形
直角三角形
A
B
C
D
E
F
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
归纳
相同点:三角形三条高所在的直线交于一点.
不同点:
锐角三角形三条高的交点在三角形的内部;
直角三角形三条高的交点在直角顶点;
钝角三角形三条高的交点在三角形的外部.
思考
你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
A
B
C
三角形的中线:
三角形中,连接一个顶点与它对边中点的线段叫作三角形的中线.
D
E
F
符号语言:
∵AD是△ABC的BC边的中线,
∴BD DC BC.
操作
任意画一个三角形,画出它的所有中线,它们有什么特点?
A
B
C
D
E
F
A
B
C
锐角三角形
直角三角形
A
B
C
钝角三角形
(1)任何三角形有三条中线,并且都在三角形的内部,交于一点;
● 三角形的中线的特征:
(2)三角形的中线是一条线段;
(3)三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.
归纳
A
B
C
D
E
F
三角形的重心:
三角形三条中线的交点叫作三角形的重心.
O
思考
C
A
B
准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕AD把∠ABC分成∠1和∠2两个角.∠1和∠2有什么关系?
C
A
B
C
A
B
D
C'
1
2
三角形的角平分线:
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫作三角形的角平分线.
符号语言:∵AD是△ABC的∠BAC的平分线,∴∠1 ∠2 ∠BAC.
操作
任意画一个三角形,画出它的所有角平分线,它们有什么特点?
C
A
B
D
F
F
A
B
C
C
B
A
锐角三角形
直角三角形
钝角三角形
三角形的三条角平分线在三角形的内部交于一点.
归纳
三角形的高
三角形的
中线
三角形的
角平分线
图形
特点
数量
3
3
3
位置
三条高所在的直线交于一点
在三角形内部、外部、三角形上
三条中线在三角形内部交于一点
三条角平分线在三角形内部交于一点
典型例题
例1 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC 60°,∠BCE 40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC 60°,
∴∠DAC ∠BAD 30°.
∵CE是△ABC的高,∠BCE 40°,
∴∠B 50°.
∴∠ADB 180° ∠B ∠BAD
180° 30° 50° 100°.
A
B
C
D
E
30°
40°
典型例题
例2 在△ABC中,CD是中线,已知BC AC 5cm,△DBC的周长为25cm,求△ADC的周长.
解:∵CD是△ABC的中线,
∴BD AD.
又∵BC AC 5cm,
△DBC的周长 BC BD CD 25cm,
∴△ADC的周长 AD CD AC
BD CD BC 5
25 5
20(cm).
A
D
B
C
AC (BC 5) cm
抢答
随堂练习
1.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
A
B
C
D
分析:
锐角三角形三条高的交点在三角形的内部;
直角三角形三条高的交点在直角顶点;
钝角三角形三条高的交点在三角形的外部.
抢答
随堂练习
2. 三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
分析:
三角形一边上的中线,把原三角形分成底相等、高相同的两个三角形,两个三角形等底同高则面积相等.
B
A
B
C
D
抢答
随堂练习
3.如图,在△ABC中,∠BAC 60°,∠B 45°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
解:∵AD是△ABC的角平分线,∠BAC 60°,
∴∠BAD ∠DAC 30°.
∵ 在△ABD中,∠B ∠ADB ∠BAD 180°,
∴∠ADB 180° ∠B ∠BAD
180° 45° 30° 105°.
三角形中几条重要的线段
三角形的几条重要线段:
高线:从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,也叫做三角形的高.
中线:三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
角平分线:三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
教科书第70页练习
