15.1 轴对称图形(共52张PPT)2025年秋沪科版八年级数学上册
文档属性
| 名称 | 15.1 轴对称图形(共52张PPT)2025年秋沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 00:00:00 | ||
图片预览








文档简介
(共52张PPT)
第15章 轴对称图形与等腰三角形
15.1 轴对称图形
第1课时
1.观察身边的图形,能识别轴对称图形.
2.能找出并画出轴对称图形的所有对称轴.
3.知道剪纸图形中的轴对称图形,想象对称轴两边的图案.
◎重点:识别轴对称图形.
◎难点:剪纸中的轴对称图形.
拿一张草稿纸,将其对折,使折线两边完全重合,任意裁剪一个图案之后,打开.观察折线两边的图案,有什么关系呢?
轴对称图形
揭示概念:如果一个平面图形沿一条直线 折叠 后,直线两旁的部分能够互相 重合 ,那么这个图形叫作 轴对称 图形,这条直线叫作 对称轴 .
学法指导:一个轴对称图形在书本上,我们不可能把书本剪掉,再将其对折.但是,我们可以通过空间想象这个图形折叠后的样子,发展空间想象的思维能力.
折叠
重合
轴对称
对称轴
·导学建议·
本节课内容较简单,应多进行一些课堂活动,让学生从实际操作中体验数学知识的应用,激发学生的学习兴趣.
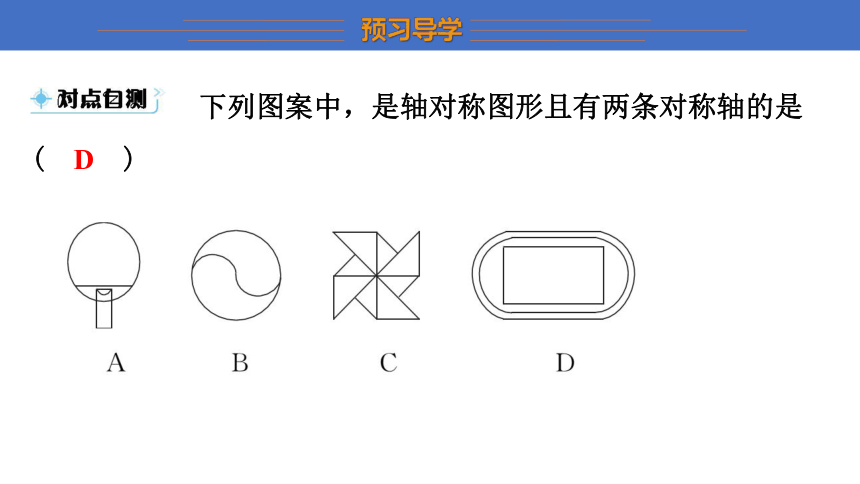
下列图案中,是轴对称图形且有两条对称轴的是
( D )
D
轴对称图形
1.如图,羊字象征吉祥和美好,下图的图案与羊有关,其中是轴对称图形的有( B )
A.1个 B.2个 C.3个 D.4个
B
【方法归纳交流】判断一个图形是不是轴对称图形,关键是找“对称轴”,可以用铅笔作出“对称轴”,仔细观察“这条直线”两旁的部分能不能完全重合.
画轴对称图形
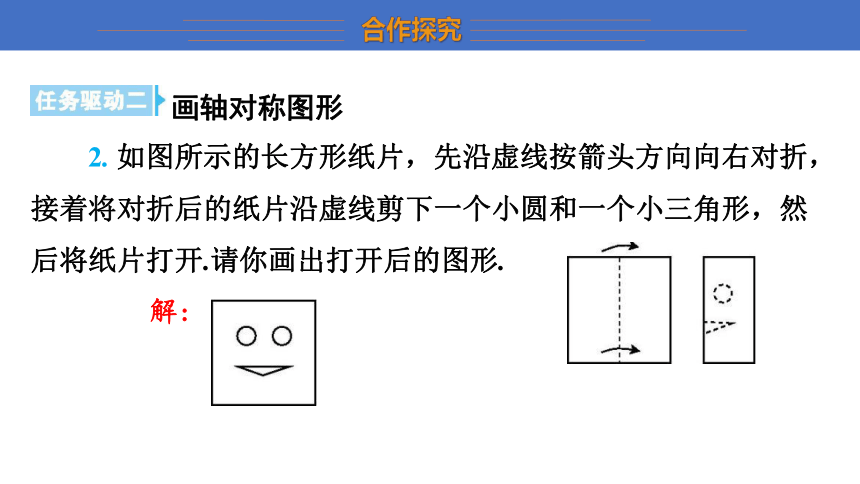
2. 如图所示的长方形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开.请你画出打开后的图形.
解:
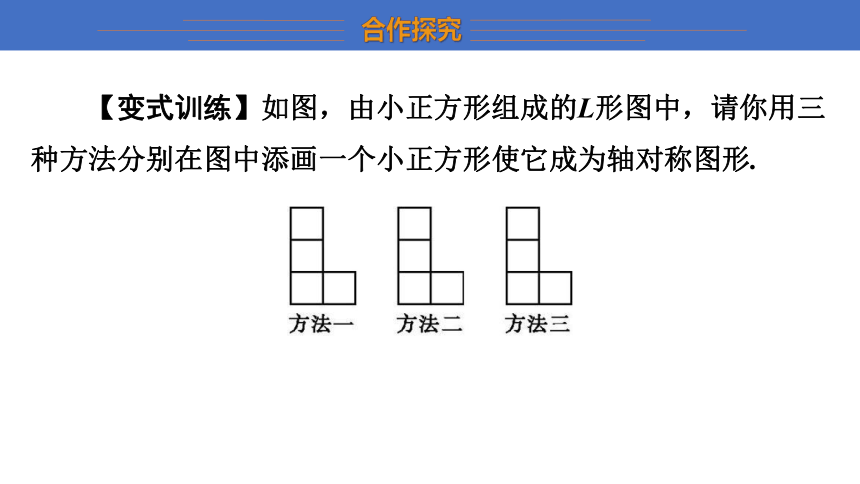
【变式训练】如图,由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形.
解:本题不同于直接作出一个图形的轴对称,这需要先找准对称轴,然后才能把轴对称图形补充完整.比如,可以得到以下补充后的轴对称称图形.
画对称轴
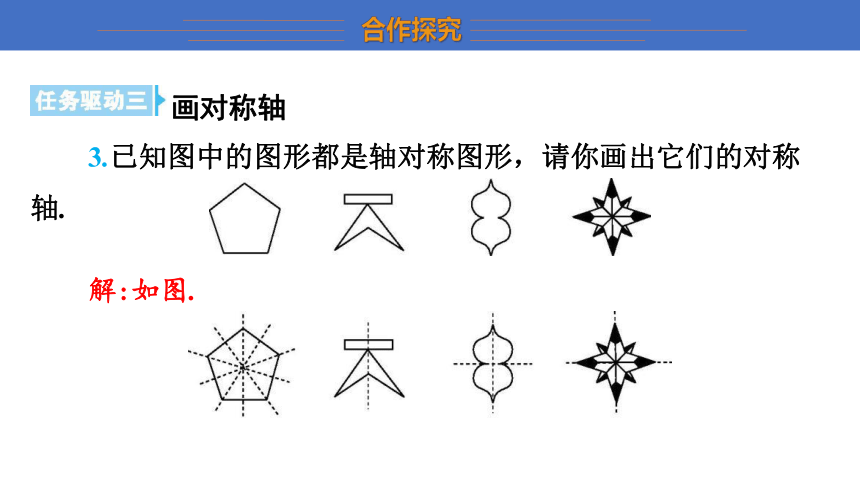
3.已知图中的图形都是轴对称图形,请你画出它们的对称轴.
解:如图.
1.小惠学习了轴对称的知识以后,忽然想起了过去做过的一道题目:有一组数排列成方阵(如图),试计算这组数的和.小惠想,方阵就是正方形,正方形是轴对称图形,能不能利用轴对称的性质来解决方阵的计算问题呢?她试了试,竟然得到了一种非常巧妙的方法,你也试试看吧!
解:正方形的一条对角线上的数都是5,把这条对角线作为对称轴对折,对称位置的两数之和都是10,这样方阵中数的和=10×10+5×5=125.
2.如图,这是未完成的某汽车的标志图案,该图案是以直线l为对称轴的轴对称图形,现已经完成对称轴左边的部分,请你补全标志图案,画出对称轴右边的部分.
图略.
15.1 轴对称图形
第2课时
1.掌握轴对称的概念,知道轴对称是一种图形变换.
2.知道两个图形成轴对称和轴对称图形的联系和区别.
3.知道轴对称的性质,会根据轴对称的性质作图.
◎重点:轴对称的概念与性质.
◎难点:两个图形成轴对称的性质.
同学们,我们在生活中都见过水中的倒影,
倒影与实际的物体之间存在着联系,数学中我们称之为轴对称现象,而水平面就是对称轴.
本节课,我们一起来探究轴对称的有关知识.
轴对称
阅读教材“思考”之前的内容,解决下列问题.
1.揭示概念:平面内 两 个图形在 一条 直线的两旁,如果沿这条直线 折叠 ,这两个图形能够重合,那么称这两个图形成 轴对称 ,这条直线叫作对称轴,折叠后重合的两点叫作 对应点 (也叫对称点).
两
一条
折叠
轴对称
对应点
2.轴对称图形与两个图形成轴对称的区别和联系
轴对称图形 两个图形成轴对称
区别 一 个图形 两 个图形
联系 1.沿着某条直线对折后,直线两旁的部分都能够 互相重合 . 2.都有 对称轴 . 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线 对称 ;如果把两个成轴对称的图形看成一个图形,那么这个图形就是 轴对称图形 一
两
互相重
合
对称轴
对称
轴对称图
形
学法指导:注意区分“轴对称图形”“轴对称”“两个图形成轴对称”表达的不同,轴对称是一种图形变换.
轴对称的性质
阅读教材本课时“思考”及其后面的内容,回答下列问题.
1.明晰概念:经过线段的 中点 并且 垂直 于这条线段的直线叫作这条线段的 垂直平分线 ,又叫作线段的 中垂线 .
中点
垂直
垂直平分线
中垂
线
2.如果两个图形关于某条直线成轴对称,那么对称轴是任何一对对应点所连线段的 垂直平分线 ;反过来,成轴对称的两个图形中,对应点的连线被对称轴 垂直平分 .
垂直平分线
垂直平分
1.下列选项中的右边图形与左边图形成轴对称的是( C )
C
2.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( B )
A B
B
C D
轴对称图形的判定
1.下面两幅图中成轴对称的有 (1)(2) .
(1)(2)
镜面对称
2.小明从镜子里看到镜子对面电子钟的像如图所示,则实际时间是( C )
A.21:10 B.10:21
C.10:51 D.12:01
C
画轴对称图形
3.已知直线l和△ABC,画△A'B'C',使得它与△ABC关于直线l对称.
解:画图略,关键画出三角形三个对应顶点的对称点.
【变式训练】如图,△ABC与△A'B'C'关于直线l对称,点A、B、C分别是点A'、B'、C'的对称点.连接A A',设A A'与直线l交于点O.
(1)直线l与线段AA'有怎样的位置关系?
(2)OA 与OA'的长度有何关系,
OB与OB',OC与OC'呢?
解:(1)直线l⊥AA'.
(2)OA=OA',OB=OB',OC=OC'.
4.如图,在正方形网格中有一个格点△ABC(即三角形的顶点都在格点上),作出△ABC关于直线l对称的△A1B1C1.(要求:A与A1,B与B1,C与C1相对应)
解:
【方法归纳交流】根据轴对称性质作图的关键是寻找已知图形上的特殊点,作出关于对称轴的对称点,将对称点进行连线即可.
1.如图,已知台球桌ABCD内有两球P、Q,现击打球Q去撞击AD边后反弹,再正面撞击球P.请画出球Q撞击AD边的位置.
解:要使球Q撞击AD边反弹,再撞击球P,必须使球Q的入射角等于反射角,显然,作点P关于AD的对称点P',连接P'Q,P'Q与AD相交于点E,容易得到∠QED=∠AEP'=∠AEP,所以点E即为所求.
2.如图,已知格点△ABC.
(1)作△ABC关于直线MN的对称图形△A'B'C'(不写作法).
(2)若方格上最小的正方形的边长为1,求△A'B'C'的面积.
解:(1)图略.
(2)△A'B'C'的面积为4.
15.1 轴对称图形
第3课时
1.在平面直角坐标系中,知道关于x轴、y轴对称的点的坐标规律.
2.探究坐标系中,图形关于x轴或y轴对称的变化规律,体会从特殊到一般的过程.
◎重点:探究关于坐标轴对称的点的变化规律.
◎难点:探究规律,从特殊到一般.
上节课,我们知道要作一个图形关于一条直线对称后的图形,应先做出对应点,再连线.那么,在平面直角坐标系中,如何做一个图形关于坐标轴对称后的图形呢?
坐标系中的轴对称
阅读教材本课时的所有内容,解决下列问题.
关于x轴对称的每对对称点的坐标: 横坐标 相同, 纵坐标 互为相反数.关于y轴对称的每对对称点的坐标: 纵坐标 相同, 横坐标 互为相反数.即已知点P(x,y),它关于x轴对称的对称点的坐标为P1(x,-y),关于y
轴对称的对称点的坐标为P2(-x,y).
横坐标
纵
坐标
纵坐标
横坐标
x,-y
-x,y
完成下表.
已知点 的坐标 A(-1,4) B(-3,1) C(-4,3)
关于y轴对 称点的坐标 A1(1,4) B1(3,1) C1(4,3)
关于x轴对称点的坐标 A2(-1,-4) B2(-3,-1) C2(-4,-3)
A1(1,4)
B1(3,1)
C1(4,3)
A2(-1,-4)
B2(-3,-1)
C2(-4,-3)
关于坐标轴轴对称的点的坐标
1.与点A(5,a)关于y轴对称的点的坐标是( A )
A.(-5,a) B.(a,-5)
C.(a,5) D.(-5,-a)
A
【变式训练】在平面直角坐标系中,已知点A(2,-3),B(-3,-2),C(-5,6),则点A,B,C关于x轴的对称点A',B',C'的坐标分别为 A'(2,3) , B'(-3,2) , C'(-5,-6) ,则A,B,C关于y轴的对称点A″,B″,C″的坐标分别为 A″(-2,-3) , B″(3,-2) , C″(5,6) .
A'(2,3)
B'(-3,2)
C'(-5,
-6)
A″(-2,-3)
B″(3,-2)
C″(5,6)
2.在平面直角坐标系中,若点P(3,a)和点Q(b,-4)关于y轴对称,则a、b的值是( A )
A.a=-4,b=-3 B.a=4,b=-3
C.a=-4,b=3 D.a=4,b=3
A
【变式训练】已知点P(m,2)关于x轴对称的点的坐标为P'(3,n),求m+n的值.
解:由题意,得m=3,n=-2,
所以m+n=3+(-2)=1.
【方法归纳交流】在平面直角坐标系中,图形关于横轴(或纵轴)对称,其中对应点坐标的横坐标(或纵坐标)不变,另一个坐标变为原来的相反数.
在平面直角坐标系中画轴对称图形
3.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(1)作出△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标.
(2)作出△ABC关于y轴对称的△A″B″C″,并写出△A″B″C″三个顶点的坐标.
解:(1)所画图形如图所示,△A'B'C'即为所求,△A'B'C'三个顶点的坐标分别为A'(4,-3),B'(3,-1),C'(1,-2).
(2)所画图形如图所示,△A″B″C″即为所求,△A″B″C″三个顶点的坐标分别为A″(-4,3),B″(-3,1),C″(-1,2).
【方法归纳交流】在平面直角坐标系中,画一个图形关于某一坐标轴的对称图形,只要分别描出图形中的关键点关于这个坐标轴对称的点,再顺次连接这些对称点,就可以得到原图形关于这个坐标轴对称的图形.
平面直角坐标系中的图形变化
4.如图,按下列要求画三角形.
(1)纵坐标不变,横坐标分别加2.
(2)横坐标不变,纵坐标分别加1.
(3)纵坐标不变,横坐标分别乘以-1.
(4)横坐标不变,纵坐标分别乘以-1.
观察变化后的三角形与原三角形有什么变化?
解:(1)与原图形相比三角形的形状、大小不变,整个三角形向右平移了2个单位长度.
(2)与原图形相比,三角形的形状、大小不变,整个三角形向上平移了1个单位长度.
(3)与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于y轴对称.
(4)与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于x轴对称.
【变式训练】已知长方形ABCD关于y轴对称,平行于y轴的边AB的长是6,点A的坐标是(-2,-1),请你写出B、C、D三点的坐标.
解:B(-2,5),C(2,5),D(2,-1)或B(-2,-7),C(2,-7),D(2,-1).
学法指导:学习点的坐标变化规律,应结合图形,遵循从特殊到一般的规律,寻找坐标轴的对称点的特征.
1.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,即第1次作原图形关于x轴对称,第2次作上一次变换后的图形关于y轴对称,第3次作上一次变换后的图形关于x轴对称,第4次作上一次变换后的图形关于y轴对称…,若原来点A的坐标是(a,b),则经过第2015次变换后所得的点A的对应点的坐标是 (-a,b) .
(-a,b)
2.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴的正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
解:(1)如图,△A1B1C1即为所求作的三角形;点B1的坐标为(-2,-1).
(2)如图,△A2B2C2即为所求作的三角形;点C2的坐标为(1,1).
第15章 轴对称图形与等腰三角形
15.1 轴对称图形
第1课时
1.观察身边的图形,能识别轴对称图形.
2.能找出并画出轴对称图形的所有对称轴.
3.知道剪纸图形中的轴对称图形,想象对称轴两边的图案.
◎重点:识别轴对称图形.
◎难点:剪纸中的轴对称图形.
拿一张草稿纸,将其对折,使折线两边完全重合,任意裁剪一个图案之后,打开.观察折线两边的图案,有什么关系呢?
轴对称图形
揭示概念:如果一个平面图形沿一条直线 折叠 后,直线两旁的部分能够互相 重合 ,那么这个图形叫作 轴对称 图形,这条直线叫作 对称轴 .
学法指导:一个轴对称图形在书本上,我们不可能把书本剪掉,再将其对折.但是,我们可以通过空间想象这个图形折叠后的样子,发展空间想象的思维能力.
折叠
重合
轴对称
对称轴
·导学建议·
本节课内容较简单,应多进行一些课堂活动,让学生从实际操作中体验数学知识的应用,激发学生的学习兴趣.
下列图案中,是轴对称图形且有两条对称轴的是
( D )
D
轴对称图形
1.如图,羊字象征吉祥和美好,下图的图案与羊有关,其中是轴对称图形的有( B )
A.1个 B.2个 C.3个 D.4个
B
【方法归纳交流】判断一个图形是不是轴对称图形,关键是找“对称轴”,可以用铅笔作出“对称轴”,仔细观察“这条直线”两旁的部分能不能完全重合.
画轴对称图形
2. 如图所示的长方形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开.请你画出打开后的图形.
解:
【变式训练】如图,由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形.
解:本题不同于直接作出一个图形的轴对称,这需要先找准对称轴,然后才能把轴对称图形补充完整.比如,可以得到以下补充后的轴对称称图形.
画对称轴
3.已知图中的图形都是轴对称图形,请你画出它们的对称轴.
解:如图.
1.小惠学习了轴对称的知识以后,忽然想起了过去做过的一道题目:有一组数排列成方阵(如图),试计算这组数的和.小惠想,方阵就是正方形,正方形是轴对称图形,能不能利用轴对称的性质来解决方阵的计算问题呢?她试了试,竟然得到了一种非常巧妙的方法,你也试试看吧!
解:正方形的一条对角线上的数都是5,把这条对角线作为对称轴对折,对称位置的两数之和都是10,这样方阵中数的和=10×10+5×5=125.
2.如图,这是未完成的某汽车的标志图案,该图案是以直线l为对称轴的轴对称图形,现已经完成对称轴左边的部分,请你补全标志图案,画出对称轴右边的部分.
图略.
15.1 轴对称图形
第2课时
1.掌握轴对称的概念,知道轴对称是一种图形变换.
2.知道两个图形成轴对称和轴对称图形的联系和区别.
3.知道轴对称的性质,会根据轴对称的性质作图.
◎重点:轴对称的概念与性质.
◎难点:两个图形成轴对称的性质.
同学们,我们在生活中都见过水中的倒影,
倒影与实际的物体之间存在着联系,数学中我们称之为轴对称现象,而水平面就是对称轴.
本节课,我们一起来探究轴对称的有关知识.
轴对称
阅读教材“思考”之前的内容,解决下列问题.
1.揭示概念:平面内 两 个图形在 一条 直线的两旁,如果沿这条直线 折叠 ,这两个图形能够重合,那么称这两个图形成 轴对称 ,这条直线叫作对称轴,折叠后重合的两点叫作 对应点 (也叫对称点).
两
一条
折叠
轴对称
对应点
2.轴对称图形与两个图形成轴对称的区别和联系
轴对称图形 两个图形成轴对称
区别 一 个图形 两 个图形
联系 1.沿着某条直线对折后,直线两旁的部分都能够 互相重合 . 2.都有 对称轴 . 3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线 对称 ;如果把两个成轴对称的图形看成一个图形,那么这个图形就是 轴对称图形 一
两
互相重
合
对称轴
对称
轴对称图
形
学法指导:注意区分“轴对称图形”“轴对称”“两个图形成轴对称”表达的不同,轴对称是一种图形变换.
轴对称的性质
阅读教材本课时“思考”及其后面的内容,回答下列问题.
1.明晰概念:经过线段的 中点 并且 垂直 于这条线段的直线叫作这条线段的 垂直平分线 ,又叫作线段的 中垂线 .
中点
垂直
垂直平分线
中垂
线
2.如果两个图形关于某条直线成轴对称,那么对称轴是任何一对对应点所连线段的 垂直平分线 ;反过来,成轴对称的两个图形中,对应点的连线被对称轴 垂直平分 .
垂直平分线
垂直平分
1.下列选项中的右边图形与左边图形成轴对称的是( C )
C
2.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( B )
A B
B
C D
轴对称图形的判定
1.下面两幅图中成轴对称的有 (1)(2) .
(1)(2)
镜面对称
2.小明从镜子里看到镜子对面电子钟的像如图所示,则实际时间是( C )
A.21:10 B.10:21
C.10:51 D.12:01
C
画轴对称图形
3.已知直线l和△ABC,画△A'B'C',使得它与△ABC关于直线l对称.
解:画图略,关键画出三角形三个对应顶点的对称点.
【变式训练】如图,△ABC与△A'B'C'关于直线l对称,点A、B、C分别是点A'、B'、C'的对称点.连接A A',设A A'与直线l交于点O.
(1)直线l与线段AA'有怎样的位置关系?
(2)OA 与OA'的长度有何关系,
OB与OB',OC与OC'呢?
解:(1)直线l⊥AA'.
(2)OA=OA',OB=OB',OC=OC'.
4.如图,在正方形网格中有一个格点△ABC(即三角形的顶点都在格点上),作出△ABC关于直线l对称的△A1B1C1.(要求:A与A1,B与B1,C与C1相对应)
解:
【方法归纳交流】根据轴对称性质作图的关键是寻找已知图形上的特殊点,作出关于对称轴的对称点,将对称点进行连线即可.
1.如图,已知台球桌ABCD内有两球P、Q,现击打球Q去撞击AD边后反弹,再正面撞击球P.请画出球Q撞击AD边的位置.
解:要使球Q撞击AD边反弹,再撞击球P,必须使球Q的入射角等于反射角,显然,作点P关于AD的对称点P',连接P'Q,P'Q与AD相交于点E,容易得到∠QED=∠AEP'=∠AEP,所以点E即为所求.
2.如图,已知格点△ABC.
(1)作△ABC关于直线MN的对称图形△A'B'C'(不写作法).
(2)若方格上最小的正方形的边长为1,求△A'B'C'的面积.
解:(1)图略.
(2)△A'B'C'的面积为4.
15.1 轴对称图形
第3课时
1.在平面直角坐标系中,知道关于x轴、y轴对称的点的坐标规律.
2.探究坐标系中,图形关于x轴或y轴对称的变化规律,体会从特殊到一般的过程.
◎重点:探究关于坐标轴对称的点的变化规律.
◎难点:探究规律,从特殊到一般.
上节课,我们知道要作一个图形关于一条直线对称后的图形,应先做出对应点,再连线.那么,在平面直角坐标系中,如何做一个图形关于坐标轴对称后的图形呢?
坐标系中的轴对称
阅读教材本课时的所有内容,解决下列问题.
关于x轴对称的每对对称点的坐标: 横坐标 相同, 纵坐标 互为相反数.关于y轴对称的每对对称点的坐标: 纵坐标 相同, 横坐标 互为相反数.即已知点P(x,y),它关于x轴对称的对称点的坐标为P1(x,-y),关于y
轴对称的对称点的坐标为P2(-x,y).
横坐标
纵
坐标
纵坐标
横坐标
x,-y
-x,y
完成下表.
已知点 的坐标 A(-1,4) B(-3,1) C(-4,3)
关于y轴对 称点的坐标 A1(1,4) B1(3,1) C1(4,3)
关于x轴对称点的坐标 A2(-1,-4) B2(-3,-1) C2(-4,-3)
A1(1,4)
B1(3,1)
C1(4,3)
A2(-1,-4)
B2(-3,-1)
C2(-4,-3)
关于坐标轴轴对称的点的坐标
1.与点A(5,a)关于y轴对称的点的坐标是( A )
A.(-5,a) B.(a,-5)
C.(a,5) D.(-5,-a)
A
【变式训练】在平面直角坐标系中,已知点A(2,-3),B(-3,-2),C(-5,6),则点A,B,C关于x轴的对称点A',B',C'的坐标分别为 A'(2,3) , B'(-3,2) , C'(-5,-6) ,则A,B,C关于y轴的对称点A″,B″,C″的坐标分别为 A″(-2,-3) , B″(3,-2) , C″(5,6) .
A'(2,3)
B'(-3,2)
C'(-5,
-6)
A″(-2,-3)
B″(3,-2)
C″(5,6)
2.在平面直角坐标系中,若点P(3,a)和点Q(b,-4)关于y轴对称,则a、b的值是( A )
A.a=-4,b=-3 B.a=4,b=-3
C.a=-4,b=3 D.a=4,b=3
A
【变式训练】已知点P(m,2)关于x轴对称的点的坐标为P'(3,n),求m+n的值.
解:由题意,得m=3,n=-2,
所以m+n=3+(-2)=1.
【方法归纳交流】在平面直角坐标系中,图形关于横轴(或纵轴)对称,其中对应点坐标的横坐标(或纵坐标)不变,另一个坐标变为原来的相反数.
在平面直角坐标系中画轴对称图形
3.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(1)作出△ABC关于x轴对称的△A'B'C',并写出△A'B'C'三个顶点的坐标.
(2)作出△ABC关于y轴对称的△A″B″C″,并写出△A″B″C″三个顶点的坐标.
解:(1)所画图形如图所示,△A'B'C'即为所求,△A'B'C'三个顶点的坐标分别为A'(4,-3),B'(3,-1),C'(1,-2).
(2)所画图形如图所示,△A″B″C″即为所求,△A″B″C″三个顶点的坐标分别为A″(-4,3),B″(-3,1),C″(-1,2).
【方法归纳交流】在平面直角坐标系中,画一个图形关于某一坐标轴的对称图形,只要分别描出图形中的关键点关于这个坐标轴对称的点,再顺次连接这些对称点,就可以得到原图形关于这个坐标轴对称的图形.
平面直角坐标系中的图形变化
4.如图,按下列要求画三角形.
(1)纵坐标不变,横坐标分别加2.
(2)横坐标不变,纵坐标分别加1.
(3)纵坐标不变,横坐标分别乘以-1.
(4)横坐标不变,纵坐标分别乘以-1.
观察变化后的三角形与原三角形有什么变化?
解:(1)与原图形相比三角形的形状、大小不变,整个三角形向右平移了2个单位长度.
(2)与原图形相比,三角形的形状、大小不变,整个三角形向上平移了1个单位长度.
(3)与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于y轴对称.
(4)与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于x轴对称.
【变式训练】已知长方形ABCD关于y轴对称,平行于y轴的边AB的长是6,点A的坐标是(-2,-1),请你写出B、C、D三点的坐标.
解:B(-2,5),C(2,5),D(2,-1)或B(-2,-7),C(2,-7),D(2,-1).
学法指导:学习点的坐标变化规律,应结合图形,遵循从特殊到一般的规律,寻找坐标轴的对称点的特征.
1.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,即第1次作原图形关于x轴对称,第2次作上一次变换后的图形关于y轴对称,第3次作上一次变换后的图形关于x轴对称,第4次作上一次变换后的图形关于y轴对称…,若原来点A的坐标是(a,b),则经过第2015次变换后所得的点A的对应点的坐标是 (-a,b) .
(-a,b)
2.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴的正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
解:(1)如图,△A1B1C1即为所求作的三角形;点B1的坐标为(-2,-1).
(2)如图,△A2B2C2即为所求作的三角形;点C2的坐标为(1,1).
