2025届上海复兴中学高一下学期数学期末试卷(2025.06)(含部分答案)
文档属性
| 名称 | 2025届上海复兴中学高一下学期数学期末试卷(2025.06)(含部分答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 00:00:00 | ||
图片预览



文档简介
复兴中学2024-2025学年第二学期高一年级数学期末
2025.6
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.已知扇形的弧长和半径都是4,则扇形的面积为________.
2.1与9的等差中项为________.
3.已知,,若,则实数________.
4.若复数满足,为虚数单位,则的实部为________.
5.已知,则________.
6.已知向量,向量,则在上的数量投影为________
7.已知等差数列满足,则________.
8.已知为虚数单位,则________.
9.设为等比数列的前项和,若,则实数________.
10.已知复数满足,则的最小值为________.
11.如图,由一个正方形与正三角形(点在下方)组成一个“风筝骨架”,为正方形的中心,点是“风筝骨架”上一点,设(、),则的最大值是________.
12.对任意闭区间,用表示函数在上的最小值.若正数满足,则正数的取值集合为________.
二、选择题(其中13~14题,每题4分,15~16题每题5分,共18分)
13.是虚数单位,复数在复平面内对应的点位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.已知数列是等比数列,、、为正整数,则“”是“”的( )条件.
A.充分非必要 B.必要非充分 C.充要 D.既非充分又非必要
15.已知向量,,,则的取值范围是( ).
A. B. C. D.
16.已知(是正整数)是直角三角形,是直角,内角、、所对的边分别为、、,面积为.若,,,.有下列两个命题:①既存在最小项又存在最大项;
②既存在最小项又存在最小项.则( ).
A.①真;②真 B.①真;②假 C.①假;②真 D.①假;②假
三、解答题(14+14+14+18+18=78分)
17.已知复数,为虚数单位.
(1)求;
(2)若复数是关于的方程的一个根,求实数,的值.
18.设是等差数列,,且,,成等比数列.
(1)求的通项公式;
(2)记的前项和为,求的最小值.
19.已知、为单位向量,且与的夹角为.
(1)求的值;
(2)若向量与的夹角为锐角,求实数的取值范围.
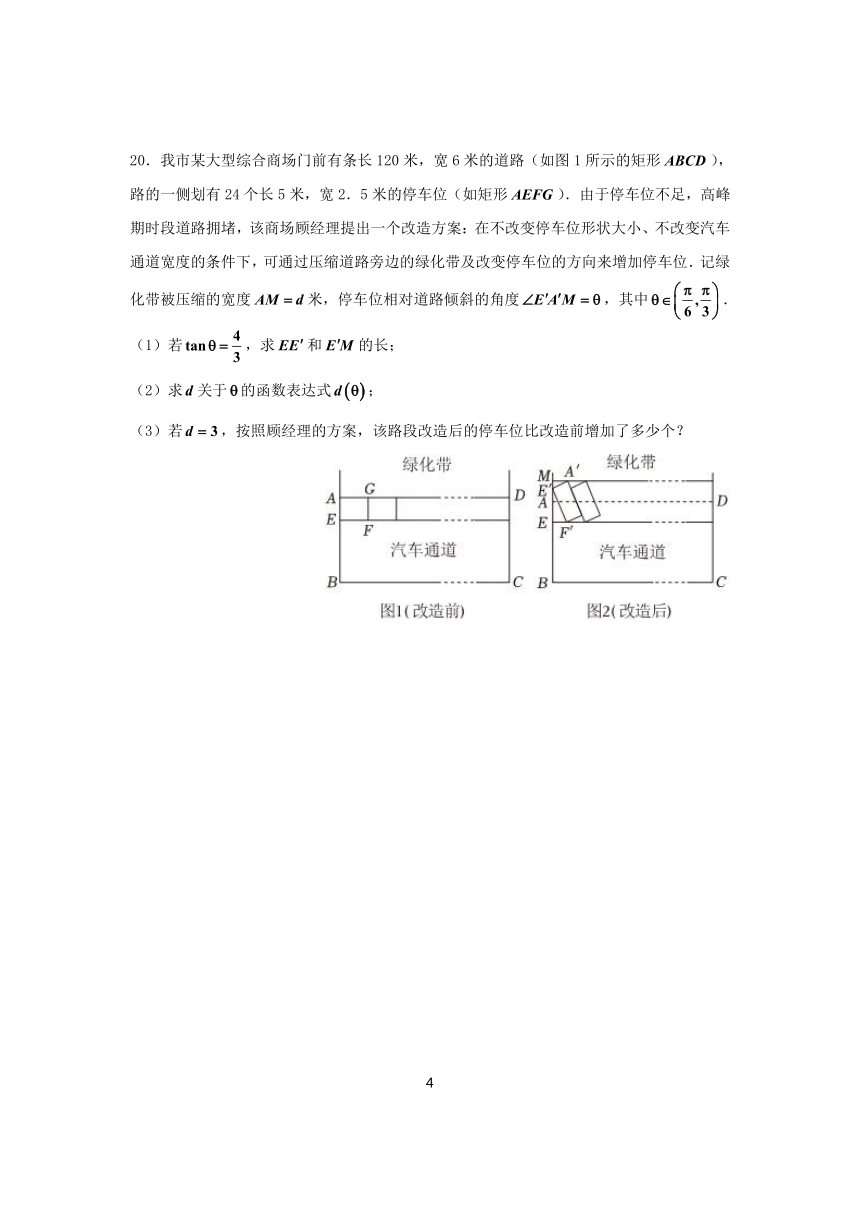
20.我市某大型综合商场门前有条长120米,宽6米的道路(如图1所示的矩形),路的一侧划有24个长5米,宽2.5米的停车位(如矩形).由于停车位不足,高峰期时段道路拥堵,该商场顾经理提出一个改造方案:在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边的绿化带及改变停车位的方向来增加停车位.记绿化带被压缩的宽度米,停车位相对道路倾斜的角度,其中.
(1)若,求和的长;
(2)求关于的函数表达式;
(3)若,按照顾经理的方案,该路段改造后的停车位比改造前增加了多少个?
21.如图,已知,,,点是的外接圆优
弧上的一个动点(含端点、),记.
(1)求外接圆的直径;
(2)试将表示为的函数;
(3)设点满足,求的最大值.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
12.对任意闭区间,用表示函数在上的最小值.若正数满足,则正数的取值集合为________.
【答案】
【解析】当时,为在上为减函数,
所以,
由,则,即
解得或,不合题意.
当时,有,,
由,则,可得.
当时,有,,不合题意;
当时,有,,适合题意;
当时,的区间长度不小于,故,适合题意.
综上正数的取值范围为或.故答案为:或.
二、选择题
13.A 14.C 15.D 16.
15.已知向量,,,则的取值范围是( ).
A. B. C. D.
【答案】D
【解析】根据题意,向量,则,
则(,又由,则有,
则有,即的取值范围是.故选:D.
三、解答题
17.(1) (2)
18.(1) (2)
19.(1) (2)
20.我市某大型综合商场门前有条长120米,宽6米的道路(如图1所示的矩形),路的一侧划有24个长5米,宽2.5米的停车位(如矩形).由于停车位不足,高峰期时段道路拥堵,该商场顾经理提出一个改造方案:在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边的绿化带及改变停车位的方向来增加停车位.记绿化带被压缩的宽度米,停车位相对道路倾斜的角度,其中.
(1)若,求和的长;
(2)求关于的函数表达式;
(3)若,按照顾经理的方案,该路段改造后的停车位比改造前增加了多少个?
【答案】(1)米,米 (2) (3)13个
【解析】(1)由题意得
则,即.
由,可得,则米,
(2)由(1)可得,
,故.
(3)由,可得,即.
设,则
整理得,解得.由,可得.
当时,解得,不符合题意;
当时,解得,符合题意.
设改造后停车位数量的最大值为,如图,过停车位顶点作的垂线,垂足为,
则顶点到线段的距离为
由图及题意可知,则.
因为,所以,
,则.
由题可知,即,解得,则取,
故该路段改造后的停车位比改造前增加了
21.(1) (2) (3)略
2025.6
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.已知扇形的弧长和半径都是4,则扇形的面积为________.
2.1与9的等差中项为________.
3.已知,,若,则实数________.
4.若复数满足,为虚数单位,则的实部为________.
5.已知,则________.
6.已知向量,向量,则在上的数量投影为________
7.已知等差数列满足,则________.
8.已知为虚数单位,则________.
9.设为等比数列的前项和,若,则实数________.
10.已知复数满足,则的最小值为________.
11.如图,由一个正方形与正三角形(点在下方)组成一个“风筝骨架”,为正方形的中心,点是“风筝骨架”上一点,设(、),则的最大值是________.
12.对任意闭区间,用表示函数在上的最小值.若正数满足,则正数的取值集合为________.
二、选择题(其中13~14题,每题4分,15~16题每题5分,共18分)
13.是虚数单位,复数在复平面内对应的点位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.已知数列是等比数列,、、为正整数,则“”是“”的( )条件.
A.充分非必要 B.必要非充分 C.充要 D.既非充分又非必要
15.已知向量,,,则的取值范围是( ).
A. B. C. D.
16.已知(是正整数)是直角三角形,是直角,内角、、所对的边分别为、、,面积为.若,,,.有下列两个命题:①既存在最小项又存在最大项;
②既存在最小项又存在最小项.则( ).
A.①真;②真 B.①真;②假 C.①假;②真 D.①假;②假
三、解答题(14+14+14+18+18=78分)
17.已知复数,为虚数单位.
(1)求;
(2)若复数是关于的方程的一个根,求实数,的值.
18.设是等差数列,,且,,成等比数列.
(1)求的通项公式;
(2)记的前项和为,求的最小值.
19.已知、为单位向量,且与的夹角为.
(1)求的值;
(2)若向量与的夹角为锐角,求实数的取值范围.
20.我市某大型综合商场门前有条长120米,宽6米的道路(如图1所示的矩形),路的一侧划有24个长5米,宽2.5米的停车位(如矩形).由于停车位不足,高峰期时段道路拥堵,该商场顾经理提出一个改造方案:在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边的绿化带及改变停车位的方向来增加停车位.记绿化带被压缩的宽度米,停车位相对道路倾斜的角度,其中.
(1)若,求和的长;
(2)求关于的函数表达式;
(3)若,按照顾经理的方案,该路段改造后的停车位比改造前增加了多少个?
21.如图,已知,,,点是的外接圆优
弧上的一个动点(含端点、),记.
(1)求外接圆的直径;
(2)试将表示为的函数;
(3)设点满足,求的最大值.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
12.对任意闭区间,用表示函数在上的最小值.若正数满足,则正数的取值集合为________.
【答案】
【解析】当时,为在上为减函数,
所以,
由,则,即
解得或,不合题意.
当时,有,,
由,则,可得.
当时,有,,不合题意;
当时,有,,适合题意;
当时,的区间长度不小于,故,适合题意.
综上正数的取值范围为或.故答案为:或.
二、选择题
13.A 14.C 15.D 16.
15.已知向量,,,则的取值范围是( ).
A. B. C. D.
【答案】D
【解析】根据题意,向量,则,
则(,又由,则有,
则有,即的取值范围是.故选:D.
三、解答题
17.(1) (2)
18.(1) (2)
19.(1) (2)
20.我市某大型综合商场门前有条长120米,宽6米的道路(如图1所示的矩形),路的一侧划有24个长5米,宽2.5米的停车位(如矩形).由于停车位不足,高峰期时段道路拥堵,该商场顾经理提出一个改造方案:在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边的绿化带及改变停车位的方向来增加停车位.记绿化带被压缩的宽度米,停车位相对道路倾斜的角度,其中.
(1)若,求和的长;
(2)求关于的函数表达式;
(3)若,按照顾经理的方案,该路段改造后的停车位比改造前增加了多少个?
【答案】(1)米,米 (2) (3)13个
【解析】(1)由题意得
则,即.
由,可得,则米,
(2)由(1)可得,
,故.
(3)由,可得,即.
设,则
整理得,解得.由,可得.
当时,解得,不符合题意;
当时,解得,符合题意.
设改造后停车位数量的最大值为,如图,过停车位顶点作的垂线,垂足为,
则顶点到线段的距离为
由图及题意可知,则.
因为,所以,
,则.
由题可知,即,解得,则取,
故该路段改造后的停车位比改造前增加了
21.(1) (2) (3)略
同课章节目录
