第14章 全等三角形 单元测试题(无答案) 2025-2026学年人教版八年级上册数学
文档属性
| 名称 | 第14章 全等三角形 单元测试题(无答案) 2025-2026学年人教版八年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 176.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 08:21:48 | ||
图片预览

文档简介
八年级上册数学第14章 全等三角形单元测试题
满分:120分 时间:120分钟
一、选择题(共12题,每题3分,共36分)
1.下列各组图形中,属于全等图形的是( )
A. 两个周长相等的圆 B. 两个面积相等的长方形
C. 两个完全重合的三角形 D. 两个底角相等的等腰三角形
2.已知△ABC≌△DEF,若AB=5cm,则DE的长度为( )
A. 3cm B. 5cm C. 7cm D. 不能确定
3.下列条件中,不能判定两个三角形全等的是( )
A. 两边及夹角对应相等 B. 两角及夹边对应相等
C. 三边对应相等 D. 三个角对应相等
4.如图,已知AB=AD,添加下列哪个条件不能判定△ABC≌△ADC( )
A. CB=CD B. ∠B=∠D C. ∠BAC=∠DAC D. ∠ACB=∠ACD
(第4题图) (第6题图)
5.在△ABC和△DEF中,AB=DE,∠A=∠D,若用"SAS"判定全等,还需添加的条件是( )
A. BC=EF B. ∠B=∠E C. AC=DF D. ∠C=∠F
6.如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A. PC>PD B. PC=PD C. PC7.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
A. 30° B. 50° C. 70° D. 80°
(第7题图) (第8题图)
8. 如图,BF=CE,AB=DE,添加下列条件仍不能证明△ABC≌△DEF的是( )
A. ∠B=∠DEF B. AC=DF C. AC∥DF D. ∠A=∠D
9.用直尺和圆规作一个角等于已知角的依据是( )
A. SAS B. ASA C. SSS D. AAS
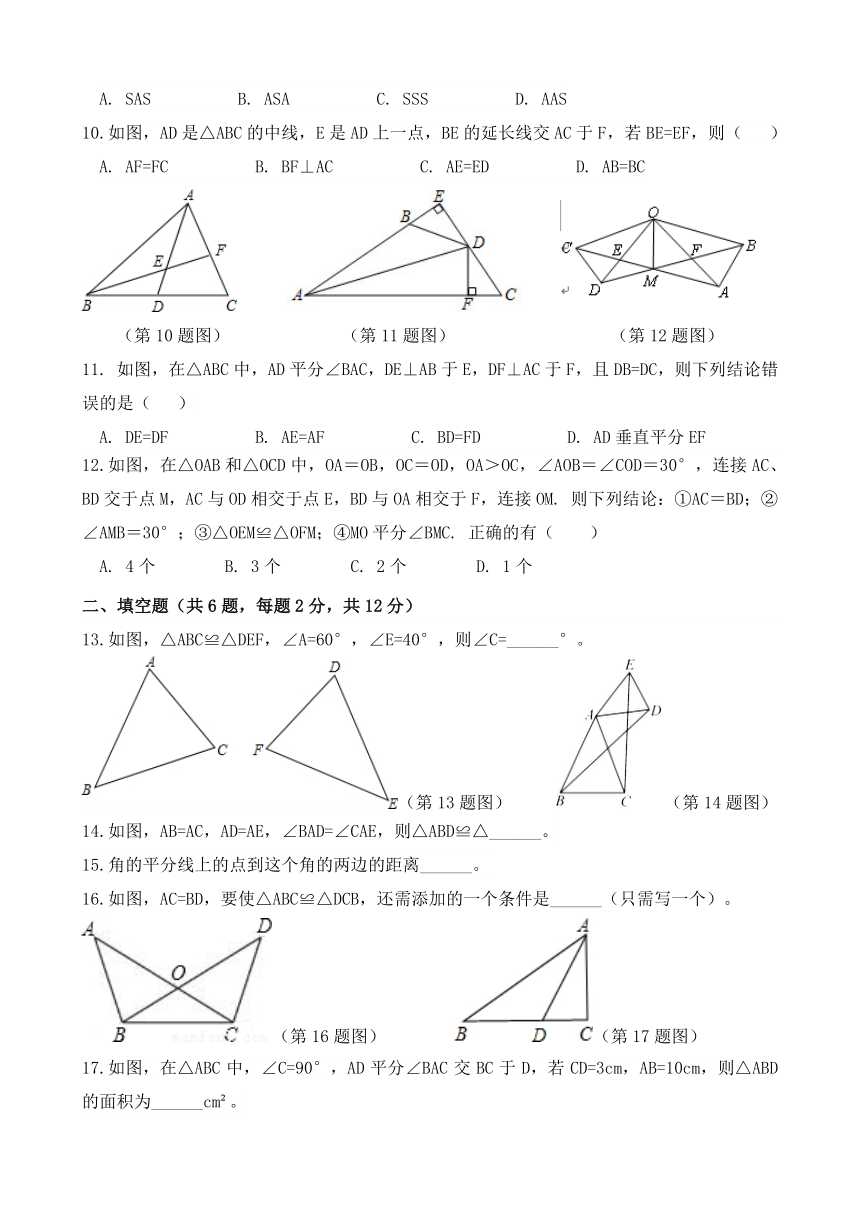
10.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,若BE=EF,则( )
A. AF=FC B. BF⊥AC C. AE=ED D. AB=BC
(第10题图) (第11题图) (第12题图)
11. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,则下列结论错误的是( )
A. DE=DF B. AE=AF C. BD=FD D. AD垂直平分EF
12.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC、BD交于点M,AC与OD相交于点E,BD与OA相交于F,连接OM. 则下列结论:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC. 正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题(共6题,每题2分,共12分)
13.如图,△ABC≌△DEF,∠A=60°,∠E=40°,则∠C=______°。
(第13题图) (第14题图)
14.如图,AB=AC,AD=AE,∠BAD=∠CAE,则△ABD≌△______。
15.角的平分线上的点到这个角的两边的距离______。
16.如图,AC=BD,要使△ABC≌△DCB,还需添加的一个条件是______(只需写一个)。
(第16题图) (第17题图)
17.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若CD=3cm,AB=10cm,则△ABD的面积为______cm 。
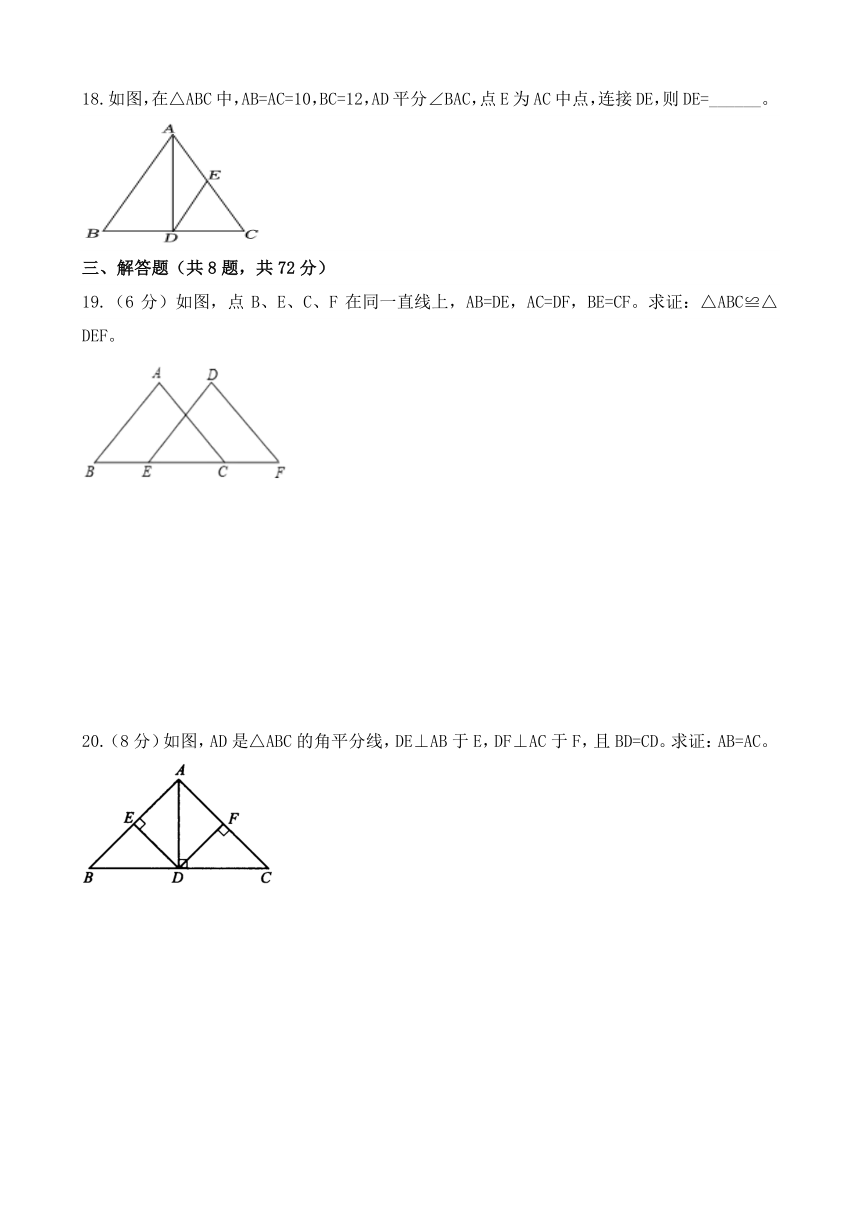
18.如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,点E为AC中点,连接DE,则DE=______。
三、解答题(共8题,共72分)
19.(6分)如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF。求证:△ABC≌△DEF。
20.(8分)如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD。求证:AB=AC。
21.(8分)如图,AB=CD,AE=CF,BF=DE。求证:△ABE≌△CDF。
22.(10分)如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。
(1)求证:△BDF≌△ADC;
(2)若AD=BD,求∠ABC的度数。
23.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于D,BE⊥MN于E。
(1)求证:△ADC≌△CEB;
(2)若AD=5cm,BE=2cm,求DE的长。
24.(12分)阅读材料,回答问题:
材料:如图1,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在AD的延长线上,且CE=CA。
(1)当∠BAC=40°时,求∠DCE的度数;(4分)
(2)当∠BAC=α时,用含α的式子表示∠DCE的度数;(4分)
(3)若AD=DE,求证:BD=CE。(4分)
25.(14分)如图,在△ABC中,∠ABC=90°,AB=BC,D为AC边上一点,连接BD,过点A作AE⊥BD于E,过点C作CF⊥BD于F。
(1)求证:△ABE≌△CBF;(6分)
(2)若AB=6,EF=2,求线段BF的长;(4分)
(3)探究AE、EF、CF之间的数量关系,并说明理由。(4分)
满分:120分 时间:120分钟
一、选择题(共12题,每题3分,共36分)
1.下列各组图形中,属于全等图形的是( )
A. 两个周长相等的圆 B. 两个面积相等的长方形
C. 两个完全重合的三角形 D. 两个底角相等的等腰三角形
2.已知△ABC≌△DEF,若AB=5cm,则DE的长度为( )
A. 3cm B. 5cm C. 7cm D. 不能确定
3.下列条件中,不能判定两个三角形全等的是( )
A. 两边及夹角对应相等 B. 两角及夹边对应相等
C. 三边对应相等 D. 三个角对应相等
4.如图,已知AB=AD,添加下列哪个条件不能判定△ABC≌△ADC( )
A. CB=CD B. ∠B=∠D C. ∠BAC=∠DAC D. ∠ACB=∠ACD
(第4题图) (第6题图)
5.在△ABC和△DEF中,AB=DE,∠A=∠D,若用"SAS"判定全等,还需添加的条件是( )
A. BC=EF B. ∠B=∠E C. AC=DF D. ∠C=∠F
6.如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A. PC>PD B. PC=PD C. PC
A. 30° B. 50° C. 70° D. 80°
(第7题图) (第8题图)
8. 如图,BF=CE,AB=DE,添加下列条件仍不能证明△ABC≌△DEF的是( )
A. ∠B=∠DEF B. AC=DF C. AC∥DF D. ∠A=∠D
9.用直尺和圆规作一个角等于已知角的依据是( )
A. SAS B. ASA C. SSS D. AAS
10.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,若BE=EF,则( )
A. AF=FC B. BF⊥AC C. AE=ED D. AB=BC
(第10题图) (第11题图) (第12题图)
11. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,则下列结论错误的是( )
A. DE=DF B. AE=AF C. BD=FD D. AD垂直平分EF
12.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC、BD交于点M,AC与OD相交于点E,BD与OA相交于F,连接OM. 则下列结论:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC. 正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题(共6题,每题2分,共12分)
13.如图,△ABC≌△DEF,∠A=60°,∠E=40°,则∠C=______°。
(第13题图) (第14题图)
14.如图,AB=AC,AD=AE,∠BAD=∠CAE,则△ABD≌△______。
15.角的平分线上的点到这个角的两边的距离______。
16.如图,AC=BD,要使△ABC≌△DCB,还需添加的一个条件是______(只需写一个)。
(第16题图) (第17题图)
17.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若CD=3cm,AB=10cm,则△ABD的面积为______cm 。
18.如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,点E为AC中点,连接DE,则DE=______。
三、解答题(共8题,共72分)
19.(6分)如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF。求证:△ABC≌△DEF。
20.(8分)如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD。求证:AB=AC。
21.(8分)如图,AB=CD,AE=CF,BF=DE。求证:△ABE≌△CDF。
22.(10分)如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。
(1)求证:△BDF≌△ADC;
(2)若AD=BD,求∠ABC的度数。
23.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于D,BE⊥MN于E。
(1)求证:△ADC≌△CEB;
(2)若AD=5cm,BE=2cm,求DE的长。
24.(12分)阅读材料,回答问题:
材料:如图1,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在AD的延长线上,且CE=CA。
(1)当∠BAC=40°时,求∠DCE的度数;(4分)
(2)当∠BAC=α时,用含α的式子表示∠DCE的度数;(4分)
(3)若AD=DE,求证:BD=CE。(4分)
25.(14分)如图,在△ABC中,∠ABC=90°,AB=BC,D为AC边上一点,连接BD,过点A作AE⊥BD于E,过点C作CF⊥BD于F。
(1)求证:△ABE≌△CBF;(6分)
(2)若AB=6,EF=2,求线段BF的长;(4分)
(3)探究AE、EF、CF之间的数量关系,并说明理由。(4分)
同课章节目录
