2026届高考数学一轮复习备考专题训练:空间向量与立体几何(真题演练)
文档属性
| 名称 | 2026届高考数学一轮复习备考专题训练:空间向量与立体几何(真题演练) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 23:19:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2026届高考数学一轮复习备考专题训练:空间向量与立体几何(真题演练)
一、选择题
1.(2024高三下·湖南模拟)已知m,n是两条不重合的直线,,是两个不重合的平面,下列命题正确的是( )
A.若,,,则
B.若,,,,则
C.若,,,则
D.若,,,则
2.(2025·攀枝花模拟)在正方体中,、分别棱,的中点,则下列选项正确的是( )
A. B.
C.面 D.面
3.(2022·毕节模拟)在正四棱锥中,底面边长为,侧棱长为4,点P是底面ABCD内一动点,且,则当A,P两点间距离最小时,直线BP与直线SC所成角的余弦值为( )
A. B. C. D.
4.(2025·汕头模拟)设平面与长方体的六个面的夹角分别为,则的值为( )
A.2 B.3 C.4 D.6
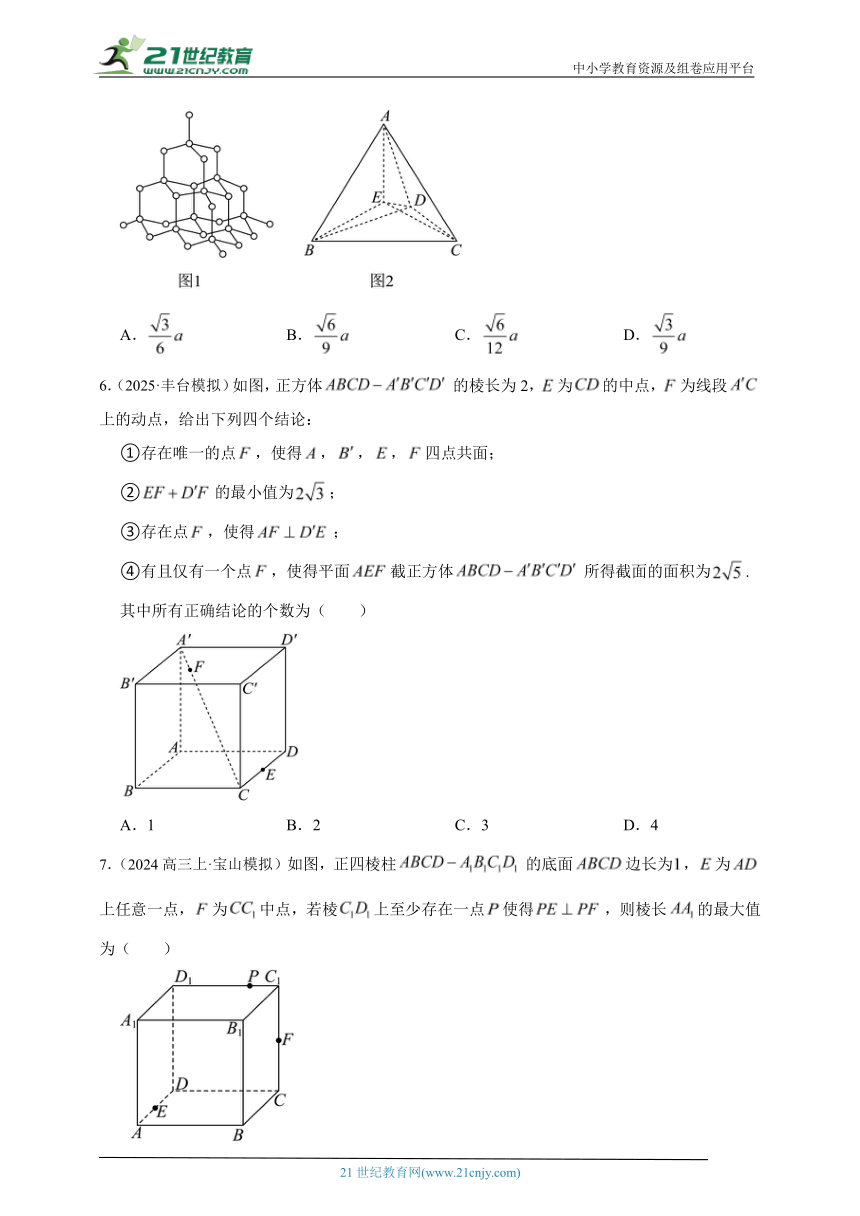
5.(2025·朝阳模拟)金刚石是由碳元素组成的单质,具有极高的硬度,在工业中有广泛的应用,如图1所示,组成金刚石的每个碳原子都与其相邻的4个碳原子以完全相同的方式连接.从立体几何的角度,可以认为4个碳原子分布在一个正四面体的4个顶点A,B,C,D处,中间的碳原子处于与这4个碳原子距离都相等的位置(点E处),如图2所示,设,则E到平面的距离为( )
A. B. C. D.
6.(2025·丰台模拟)如图,正方体的棱长为2,为的中点,为线段上的动点,给出下列四个结论:
①存在唯一的点,使得,,,四点共面;
②的最小值为;
③存在点,使得;
④有且仅有一个点,使得平面截正方体所得截面的面积为.
其中所有正确结论的个数为( )
A.1 B.2 C.3 D.4
7.(2024高三上·宝山模拟)如图,正四棱柱的底面边长为,为上任意一点,为中点,若棱上至少存在一点使得,则棱长的最大值为( )
A. B. C. D.
8.(2024高三上·虹口模拟)已知边长为2的正四面体的内切球(球面与四面体四个面都相切的球)的球心为O,若空间中的动点P满足,则点P的轨迹所形成的几何体的体积为( ).
A. B. C.. D.
二、多项选择题
9.(2025·揭阳模拟)三棱锥中,平面平面,,,其各顶点均在球O的表面上,则( )
A.
B.点A到平面的距离为
C.二面角的余弦值为
D.球O的表面积为
10.(2025·浙江模拟)正方体的棱长为,点、分别在线段、上运动(包括端点),则下列结论正确的是( )
A.正方体被经过、两点的平面所截,其截面的形状有可能是六边形
B.不可能与、都垂直
C.有可能与正方体的六个表面所成的角都相等
D.线段的中点所围成的区域的面积为
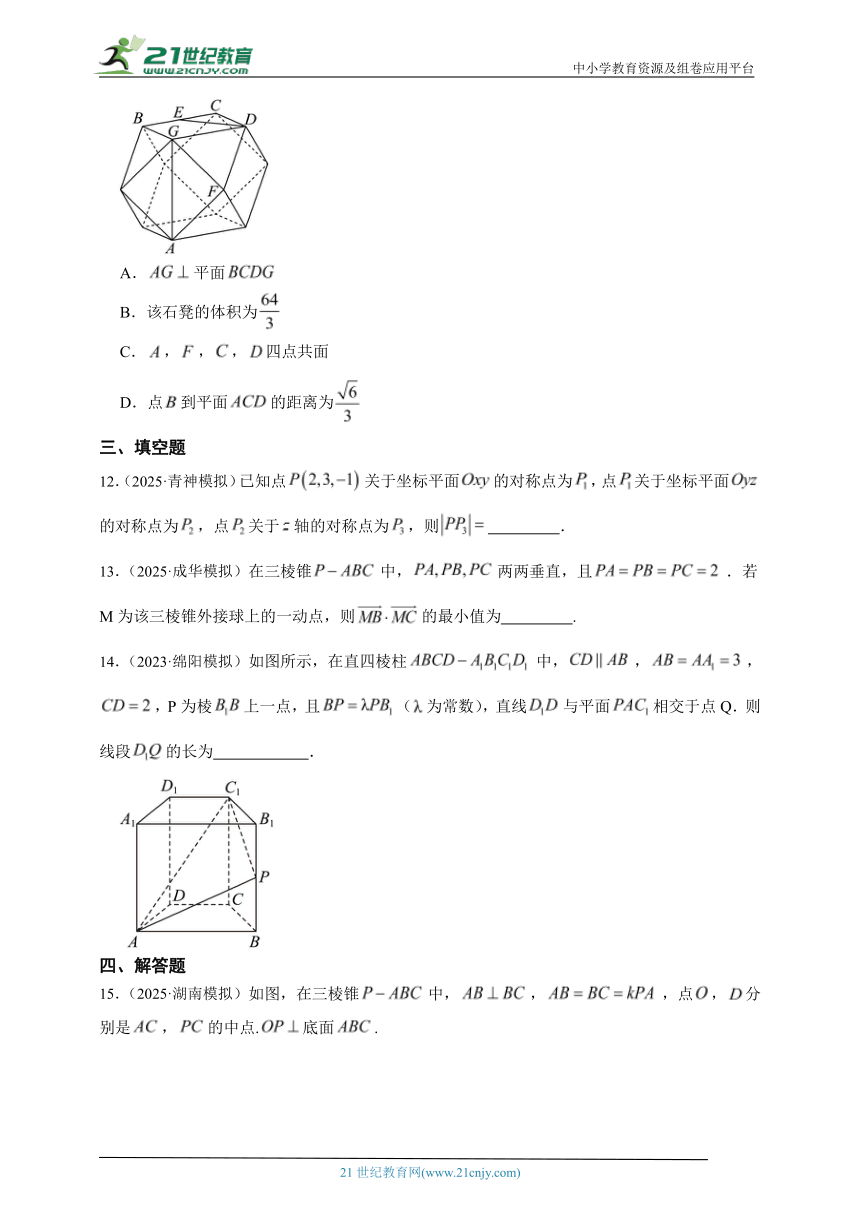
11.(2025·仁寿模拟)某广场内设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的(被称作阿基米德体),如图所示,若该石凳的棱长为,下列结论正确的有( )
A.平面
B.该石凳的体积为
C.,,,四点共面
D.点到平面的距离为
三、填空题
12.(2025·青神模拟)已知点关于坐标平面的对称点为,点关于坐标平面的对称点为,点关于轴的对称点为,则 .
13.(2025·成华模拟)在三棱锥中,两两垂直,且.若M为该三棱锥外接球上的一动点,则的最小值为 .
14.(2023·绵阳模拟)如图所示,在直四棱柱中,,,,P为棱上一点,且(为常数),直线与平面相交于点Q.则线段的长为 .
四、解答题
15.(2025·湖南模拟)如图,在三棱锥中,,,点,分别是,的中点.底面.
(1)求证:平面;
(2)当取何值时,在平面内的射影恰好为的重心?
16.(2025·安化模拟)如图,四棱锥中,底面,,,,平面PAD与平面PBC的交线为l,且.
(1)证明;
(2)若,求平面ABE与平面PCB夹角的余弦值.
17.(2025·梅河口模拟)如图,在多面体中,是边长为2的等边三角形,平面,,,,,设为的中点.
(1)证明:平面;
(2)设为棱上的动点,求与平面所成角的正弦值的最大值.
18.(2025·金川模拟)如图所示,在边长为2的正方体中,分别是棱上的点(异于端点),且.
(1)证明:与相交且交点在直线上.
(2)当直线与平面所成角的正弦值为时,求的值.
19.(2025·会宁模拟)已知四边形为矩形,四边形为直角梯形,,二面角的大小为.
(1)若为的中点.
①求点到平面的距离;
②若,求平面与平面夹角的余弦值.
(2)若,点为线段的中点,将沿折起,使得与四边形在平面的同侧,且平面平面,点为四面体的内切球球面上的一动点,求的最小值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A,B,D
10.【答案】A,C,D
11.【答案】A,C
12.【答案】
13.【答案】
14.【答案】
15.【答案】(1)证明:连接,
平面,,,
,,,
以为原点,,,所在直线为轴、轴、轴,建立空间直角坐标系(如图),
设,
则,,.
设,则,
为的中点,
,
又因为,
,
,
则,
又因为平面,平面,
平面.
(2)解:设的重心为,
则,
,
平面,
因为平面,
,
又因为,
,
,
,则,
经检验,当时,在平面内的射影为的重心,
所以.
16.【答案】(1)证明:已知平面PAD与平面PBC的交线为l,且.平面,平面,
∴平面,
∵平面平面,平面,
∴.
又,,,
由余弦定理得,
∵,
∴,
∴,
又平面,平面,
∴,
∵,平面,
∴平面,
∵平面,
∴.
即.
(2)解:由题意,以A点为原点,AB,AD,AP为x,y,z轴建立空间直角坐标系
.
,,,
平面PCB中,,,
设为面PCB的一个法向量,
则,令,则,
∴,
平面ABE中,,
,,
设为面ABE的一个法向量,
则,解得,令,则,
∴
设面PCB与面ABE所成角为θ,
则,
所以面PCB与面ABE所成夹角的余弦值为.
17.【答案】(1)证明:在平面ABC内过点作直线,因为平面,平面,所以,,
以为坐标原点,建立空间直角坐标系,如图所示:
则,,,,
因为为的中点,所以,,,,
因为,所以,
又因为平面,平面,,所以平面;
(2)解:设,即,
则,
,,
设平面的一个法向量,则,
令,求得,即,
设直线与平面所成角为,
则,
令,
当时,取最小值,即,
即当时,取得最大值,.
18.【答案】(1)证明:连接,如图所示:
因为,所以,
又因为分别是棱上异于端点的点,所以,则四边形为梯形,与相交,
记,因为平面平面,
平面平面,所以,则与的交点在直线上;
(2)解:以为原点,建立空间直角坐标系,如图所示:
设,
则,,,,
设为平面的法向量,
由,可得,
令,得,即,
设直线与平面所成的角为,
,解得,
则当直线与平面所成角的正弦值为时,.
19.【答案】(1)解:①、设的中点分别为,连接,
在平面内,过点作,垂足为,如图所示:
因为四边形为矩形,所以,
又因为,且分别为的中点,所以,所以,
因为,平面,平面,所以,
因为,且,平面,所以平面,
因为,所以.
因为,所以,则点到平面的距离为;
②过点作平面,分别以所在直线为轴,建立空间直角坐标系,如图所示:
由①知,,
由,
可得,,
,,
设平面的法向量为,平面的法向量为,
则,即,令,解得,
则为平面的一个法向量,
,即令,解得,
则为平面的一个法向量,
,
故平面与平面夹角的余弦值为;
(2)解:易知四面体是棱长为的正四面体,作平面,设内切球的球心为,建立空间直角坐标系,如图所示:
且,则.
设内切球的半径为,由等体积法知,则,
设内切球球面上任意一点为,则,
空间中必存在一定点,使球上的点满足,
即,
则,
因为,所以,解得,
易知.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026届高考数学一轮复习备考专题训练:空间向量与立体几何(真题演练)
一、选择题
1.(2024高三下·湖南模拟)已知m,n是两条不重合的直线,,是两个不重合的平面,下列命题正确的是( )
A.若,,,则
B.若,,,,则
C.若,,,则
D.若,,,则
2.(2025·攀枝花模拟)在正方体中,、分别棱,的中点,则下列选项正确的是( )
A. B.
C.面 D.面
3.(2022·毕节模拟)在正四棱锥中,底面边长为,侧棱长为4,点P是底面ABCD内一动点,且,则当A,P两点间距离最小时,直线BP与直线SC所成角的余弦值为( )
A. B. C. D.
4.(2025·汕头模拟)设平面与长方体的六个面的夹角分别为,则的值为( )
A.2 B.3 C.4 D.6
5.(2025·朝阳模拟)金刚石是由碳元素组成的单质,具有极高的硬度,在工业中有广泛的应用,如图1所示,组成金刚石的每个碳原子都与其相邻的4个碳原子以完全相同的方式连接.从立体几何的角度,可以认为4个碳原子分布在一个正四面体的4个顶点A,B,C,D处,中间的碳原子处于与这4个碳原子距离都相等的位置(点E处),如图2所示,设,则E到平面的距离为( )
A. B. C. D.
6.(2025·丰台模拟)如图,正方体的棱长为2,为的中点,为线段上的动点,给出下列四个结论:
①存在唯一的点,使得,,,四点共面;
②的最小值为;
③存在点,使得;
④有且仅有一个点,使得平面截正方体所得截面的面积为.
其中所有正确结论的个数为( )
A.1 B.2 C.3 D.4
7.(2024高三上·宝山模拟)如图,正四棱柱的底面边长为,为上任意一点,为中点,若棱上至少存在一点使得,则棱长的最大值为( )
A. B. C. D.
8.(2024高三上·虹口模拟)已知边长为2的正四面体的内切球(球面与四面体四个面都相切的球)的球心为O,若空间中的动点P满足,则点P的轨迹所形成的几何体的体积为( ).
A. B. C.. D.
二、多项选择题
9.(2025·揭阳模拟)三棱锥中,平面平面,,,其各顶点均在球O的表面上,则( )
A.
B.点A到平面的距离为
C.二面角的余弦值为
D.球O的表面积为
10.(2025·浙江模拟)正方体的棱长为,点、分别在线段、上运动(包括端点),则下列结论正确的是( )
A.正方体被经过、两点的平面所截,其截面的形状有可能是六边形
B.不可能与、都垂直
C.有可能与正方体的六个表面所成的角都相等
D.线段的中点所围成的区域的面积为
11.(2025·仁寿模拟)某广场内设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的(被称作阿基米德体),如图所示,若该石凳的棱长为,下列结论正确的有( )
A.平面
B.该石凳的体积为
C.,,,四点共面
D.点到平面的距离为
三、填空题
12.(2025·青神模拟)已知点关于坐标平面的对称点为,点关于坐标平面的对称点为,点关于轴的对称点为,则 .
13.(2025·成华模拟)在三棱锥中,两两垂直,且.若M为该三棱锥外接球上的一动点,则的最小值为 .
14.(2023·绵阳模拟)如图所示,在直四棱柱中,,,,P为棱上一点,且(为常数),直线与平面相交于点Q.则线段的长为 .
四、解答题
15.(2025·湖南模拟)如图,在三棱锥中,,,点,分别是,的中点.底面.
(1)求证:平面;
(2)当取何值时,在平面内的射影恰好为的重心?
16.(2025·安化模拟)如图,四棱锥中,底面,,,,平面PAD与平面PBC的交线为l,且.
(1)证明;
(2)若,求平面ABE与平面PCB夹角的余弦值.
17.(2025·梅河口模拟)如图,在多面体中,是边长为2的等边三角形,平面,,,,,设为的中点.
(1)证明:平面;
(2)设为棱上的动点,求与平面所成角的正弦值的最大值.
18.(2025·金川模拟)如图所示,在边长为2的正方体中,分别是棱上的点(异于端点),且.
(1)证明:与相交且交点在直线上.
(2)当直线与平面所成角的正弦值为时,求的值.
19.(2025·会宁模拟)已知四边形为矩形,四边形为直角梯形,,二面角的大小为.
(1)若为的中点.
①求点到平面的距离;
②若,求平面与平面夹角的余弦值.
(2)若,点为线段的中点,将沿折起,使得与四边形在平面的同侧,且平面平面,点为四面体的内切球球面上的一动点,求的最小值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A,B,D
10.【答案】A,C,D
11.【答案】A,C
12.【答案】
13.【答案】
14.【答案】
15.【答案】(1)证明:连接,
平面,,,
,,,
以为原点,,,所在直线为轴、轴、轴,建立空间直角坐标系(如图),
设,
则,,.
设,则,
为的中点,
,
又因为,
,
,
则,
又因为平面,平面,
平面.
(2)解:设的重心为,
则,
,
平面,
因为平面,
,
又因为,
,
,
,则,
经检验,当时,在平面内的射影为的重心,
所以.
16.【答案】(1)证明:已知平面PAD与平面PBC的交线为l,且.平面,平面,
∴平面,
∵平面平面,平面,
∴.
又,,,
由余弦定理得,
∵,
∴,
∴,
又平面,平面,
∴,
∵,平面,
∴平面,
∵平面,
∴.
即.
(2)解:由题意,以A点为原点,AB,AD,AP为x,y,z轴建立空间直角坐标系
.
,,,
平面PCB中,,,
设为面PCB的一个法向量,
则,令,则,
∴,
平面ABE中,,
,,
设为面ABE的一个法向量,
则,解得,令,则,
∴
设面PCB与面ABE所成角为θ,
则,
所以面PCB与面ABE所成夹角的余弦值为.
17.【答案】(1)证明:在平面ABC内过点作直线,因为平面,平面,所以,,
以为坐标原点,建立空间直角坐标系,如图所示:
则,,,,
因为为的中点,所以,,,,
因为,所以,
又因为平面,平面,,所以平面;
(2)解:设,即,
则,
,,
设平面的一个法向量,则,
令,求得,即,
设直线与平面所成角为,
则,
令,
当时,取最小值,即,
即当时,取得最大值,.
18.【答案】(1)证明:连接,如图所示:
因为,所以,
又因为分别是棱上异于端点的点,所以,则四边形为梯形,与相交,
记,因为平面平面,
平面平面,所以,则与的交点在直线上;
(2)解:以为原点,建立空间直角坐标系,如图所示:
设,
则,,,,
设为平面的法向量,
由,可得,
令,得,即,
设直线与平面所成的角为,
,解得,
则当直线与平面所成角的正弦值为时,.
19.【答案】(1)解:①、设的中点分别为,连接,
在平面内,过点作,垂足为,如图所示:
因为四边形为矩形,所以,
又因为,且分别为的中点,所以,所以,
因为,平面,平面,所以,
因为,且,平面,所以平面,
因为,所以.
因为,所以,则点到平面的距离为;
②过点作平面,分别以所在直线为轴,建立空间直角坐标系,如图所示:
由①知,,
由,
可得,,
,,
设平面的法向量为,平面的法向量为,
则,即,令,解得,
则为平面的一个法向量,
,即令,解得,
则为平面的一个法向量,
,
故平面与平面夹角的余弦值为;
(2)解:易知四面体是棱长为的正四面体,作平面,设内切球的球心为,建立空间直角坐标系,如图所示:
且,则.
设内切球的半径为,由等体积法知,则,
设内切球球面上任意一点为,则,
空间中必存在一定点,使球上的点满足,
即,
则,
因为,所以,解得,
易知.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
