冀教版(2024)九年级数学上册 24.4 一元二次方程的应用 课件(共21张PPT)
文档属性
| 名称 | 冀教版(2024)九年级数学上册 24.4 一元二次方程的应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第二十四章 一元二次方程
24.4 一元二次方程的应用
第3课时 销售问题及传播问题
合作探究、展示点评
合作探究、展示点评
学 习 目 标
1
2
会用一元二次方程的方法解决营销问题及传播问题.(重点、难点)
进一步培养化实际问题为数学问题的能力及分析问题解决问题的能力.
目标导学、自主提炼
传播问题与一元二次方程
问题:某少年宫组织一次足球赛,采取单循环的比赛形式,即每两个足球队之间都要比赛一场,计划安排28场比赛.可邀请多少支球队参加比赛呢
分析:设应邀请x支球队参加比赛.
(1)根据“每两个足球队之间都要比赛一场”,每支足球队要比赛 场.
(2)用含x的代数式表示比赛的总场数为 ,于是可得方
程 .
(3)解这个方程并检验结果.
合作探究、展示点评
合作探究、展示点评
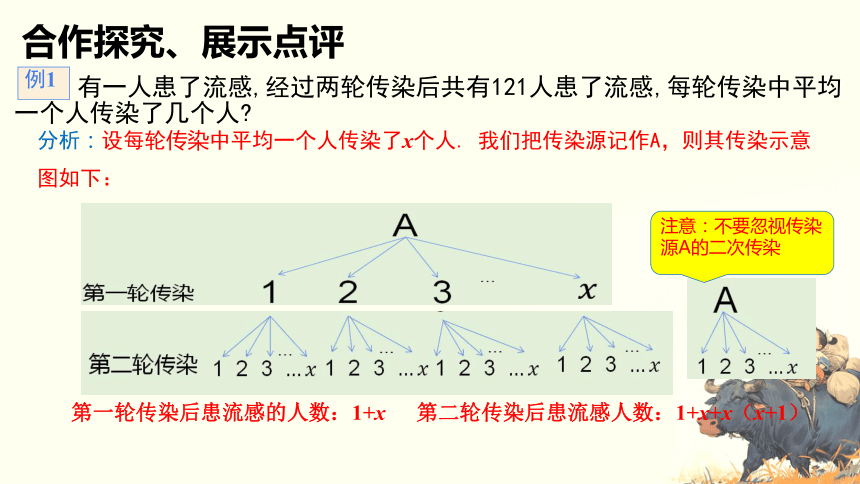
注意:不要忽视传染源A的二次传染
第一轮传染后患流感的人数:1+x
第二轮传染后患流感人数:1+x+x(x+1)
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
例1
分析:设每轮传染中平均一个人传染了x个人. 我们把传染源记作A,则其传染示意图如下:
合作探究、展示点评
x1=10, x2=-12(不合题意,舍去) .
解方程,得
答:平均一个人传染了10个人.
解:设每轮传染中平均一个人传染了x个人.根据题意,得
即(1+x)2=121,
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
1+x+x(x+1)=121,
合作探究、展示点评
思考 如果按照这样的传染速度,三轮传染后有多少人患流感
已知两轮传染后患流感的人数为:121人
第三轮新增的患流感人数为:121×10人
三轮传染后患流感的人数为:121+ 121×10=1331(人)
方法一:
合作探究、展示点评
第一轮传染后患流感的人数:1+x=(1+x)1
第二轮传染后患流感人数:1+x+x(x+1)=(1+x)2
第三轮传染后患流感人数:1+x+x(x+1)+x[1+x+x(x+1)]=(1+x)3
答案:三轮传染后的人数是:121(1+x)=121(1+10)=1331(人) 或 (1+x)3=(1+10)3=1331(人) .
方法二:
合作探究、展示点评
传播类问题
数量关系:
第一轮传染后的量=传染前的量× (1+传染速度)
第二轮传染后的量=第一轮传染后的量× (1+传染速度)=传染前的量× (1+传染速度)2
握手问题
赠礼物问题
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲和乙互赠礼物是两个礼物,故总数不要除以2
传染问题
比赛问题
甲和乙比赛与乙和甲比赛在同一次进行,所以总数要除以2
归纳总结
合作探究、展示点评
销售问题与一元二次方程
某商场经销的太阳能路灯,标价为4000元/个,优惠办法是:一次购买数量不超过80个,按标价收费;一次购买数量超过80个,每多买1个,所购路灯每个可降价8元,但单价最低不能低于3200元/个.若一顾客一次性购买这样的路灯用去516 000元,则该顾客实际购买了多少个路灯
合作探究、展示点评
(3)设该顾客购买这种路灯81个,路灯数超出80个的数量是____个,每个路灯可降价____元,则每个路灯的单价_______元.
(4)设该顾客购买这种路灯82个,路灯数超出80个的数量是____个,每个路灯可降价______元,则每个路灯的单价___________元.
(5)设该顾客购买这种路灯x(x>80)个,路灯数超出80个的数量是______个,每个路灯可降价____________元,则每个路灯的单价________________元.
(1)若顾客实际购买的路灯数量是80个,则所需费用________元
(2)若顾客一次性购买路灯用去516000元,则所买路灯数量_____个.
320000
>80
1
8
4000-8
2
8×2
4000-8×2
(x-80)
4000-8(x-80)
8(x-80)
解:因为4 000×80=320 000<516 000,所以该顾客购买路灯数量超过80个.
设该顾客购买这种路灯x个,则路灯的售价为[4000-8(x-80)]元/个.
根据题意,得x[4000-8(x-80)]=516 000.
整理,得x2-580x+64 500=0.
解这个方程,得x1=150, x2=430.
当x=430时,4 000-8(x-80)=4 000-8×(430-80)=1 200(元),低于3200元,不合题意,舍去.
答:该顾客实际购买了150个路灯.
合作探究、展示点评
合作探究、展示点评
★利润问题常见关系式
基本关系:(1)利润=售价-________;
(3)总利润=____________×销量.
进价
单个利润
效果评价、归纳总结
1.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后会有81台电脑被感染,每轮感染中平均一台电脑会感染几台电脑?设每轮感染中平均一台电脑会感染x台电脑,则x满足的方程是( )
A.1+x2=81 B.(1+x)2=81
C.1+x+x2=81 D.1+x+(1+x)2=81
2.新年里,一个小组有若干人,若每人给小组的其他成员赠送一张贺年卡,则全组送贺卡共72张,此小组人数为( )
A.7 B.8 C.9 D.10
C
B
效果评价、归纳总结
3.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查表明,这种台灯的售价每上涨1元,某销售量就将减少10台,为了实现平均每月10000元销售利润,这种台灯的售价应定为多少?这时应进台灯多少台?
解:设台灯的售价因定为 x 元.根据题意,得
(x - 30)[600 - 10 (x - 40) ] =10000.
整理,得 x2 - 130x + 4000 = 0 .
解得 x1 = 50 , x2= 80.
当x = 50 时 , 应进台灯600- 10(50 - 40)=500 (台).
当x = 80 时 , 应进台灯600- 10(80 - 40)=200 (台).
效果评价、归纳总结
5.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,问有多少家公司出席了这次交易会?
4.一条直线上有n个点,共形成了45条线段,求n的值.
效果评价、归纳总结
6.菜农李伟种植的某蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该蔬菜滞销,李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:方案一:打九折销售;方案二:不打折,每吨优惠现金200元.试问小华选择哪种方案更优惠?请说明理由.
效果评价、归纳总结
解:(1)设平均每次下调的百分率为x. 由题意,得
5(1-x)2=3.2,
解得 x1=20%,x2=1.8 (舍去)
∴平均每次下调的百分率为20%.
(2)小华选择方案一购买更优惠,理由如下:
方案一所需费用为3.2×0.9×5000=14400(元);
方案二所需费用为3.2×5000-200×5=15000(元).
∵14400<15000,
∴小华选择方案一购买更优惠.
效果评价、归纳总结
1.单循环赛问题中的等量关系:
比赛总场数=x(x-1)÷2(x为球队个数).
易错点是列方程时忽略除以2.
2.利润问题中的等量关系:
利润= (售价-进价)×销售量.
3.解决较为复杂的应用题时,要认真读懂题意,正确找到等量关系并准确表达,建立方程模型,并检验解出的根是否符合题意.
效果评价、归纳总结
第二十四章 一元二次方程
24.4 一元二次方程的应用
第3课时 销售问题及传播问题
合作探究、展示点评
合作探究、展示点评
学 习 目 标
1
2
会用一元二次方程的方法解决营销问题及传播问题.(重点、难点)
进一步培养化实际问题为数学问题的能力及分析问题解决问题的能力.
目标导学、自主提炼
传播问题与一元二次方程
问题:某少年宫组织一次足球赛,采取单循环的比赛形式,即每两个足球队之间都要比赛一场,计划安排28场比赛.可邀请多少支球队参加比赛呢
分析:设应邀请x支球队参加比赛.
(1)根据“每两个足球队之间都要比赛一场”,每支足球队要比赛 场.
(2)用含x的代数式表示比赛的总场数为 ,于是可得方
程 .
(3)解这个方程并检验结果.
合作探究、展示点评
合作探究、展示点评
注意:不要忽视传染源A的二次传染
第一轮传染后患流感的人数:1+x
第二轮传染后患流感人数:1+x+x(x+1)
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
例1
分析:设每轮传染中平均一个人传染了x个人. 我们把传染源记作A,则其传染示意图如下:
合作探究、展示点评
x1=10, x2=-12(不合题意,舍去) .
解方程,得
答:平均一个人传染了10个人.
解:设每轮传染中平均一个人传染了x个人.根据题意,得
即(1+x)2=121,
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
1+x+x(x+1)=121,
合作探究、展示点评
思考 如果按照这样的传染速度,三轮传染后有多少人患流感
已知两轮传染后患流感的人数为:121人
第三轮新增的患流感人数为:121×10人
三轮传染后患流感的人数为:121+ 121×10=1331(人)
方法一:
合作探究、展示点评
第一轮传染后患流感的人数:1+x=(1+x)1
第二轮传染后患流感人数:1+x+x(x+1)=(1+x)2
第三轮传染后患流感人数:1+x+x(x+1)+x[1+x+x(x+1)]=(1+x)3
答案:三轮传染后的人数是:121(1+x)=121(1+10)=1331(人) 或 (1+x)3=(1+10)3=1331(人) .
方法二:
合作探究、展示点评
传播类问题
数量关系:
第一轮传染后的量=传染前的量× (1+传染速度)
第二轮传染后的量=第一轮传染后的量× (1+传染速度)=传染前的量× (1+传染速度)2
握手问题
赠礼物问题
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲和乙互赠礼物是两个礼物,故总数不要除以2
传染问题
比赛问题
甲和乙比赛与乙和甲比赛在同一次进行,所以总数要除以2
归纳总结
合作探究、展示点评
销售问题与一元二次方程
某商场经销的太阳能路灯,标价为4000元/个,优惠办法是:一次购买数量不超过80个,按标价收费;一次购买数量超过80个,每多买1个,所购路灯每个可降价8元,但单价最低不能低于3200元/个.若一顾客一次性购买这样的路灯用去516 000元,则该顾客实际购买了多少个路灯
合作探究、展示点评
(3)设该顾客购买这种路灯81个,路灯数超出80个的数量是____个,每个路灯可降价____元,则每个路灯的单价_______元.
(4)设该顾客购买这种路灯82个,路灯数超出80个的数量是____个,每个路灯可降价______元,则每个路灯的单价___________元.
(5)设该顾客购买这种路灯x(x>80)个,路灯数超出80个的数量是______个,每个路灯可降价____________元,则每个路灯的单价________________元.
(1)若顾客实际购买的路灯数量是80个,则所需费用________元
(2)若顾客一次性购买路灯用去516000元,则所买路灯数量_____个.
320000
>80
1
8
4000-8
2
8×2
4000-8×2
(x-80)
4000-8(x-80)
8(x-80)
解:因为4 000×80=320 000<516 000,所以该顾客购买路灯数量超过80个.
设该顾客购买这种路灯x个,则路灯的售价为[4000-8(x-80)]元/个.
根据题意,得x[4000-8(x-80)]=516 000.
整理,得x2-580x+64 500=0.
解这个方程,得x1=150, x2=430.
当x=430时,4 000-8(x-80)=4 000-8×(430-80)=1 200(元),低于3200元,不合题意,舍去.
答:该顾客实际购买了150个路灯.
合作探究、展示点评
合作探究、展示点评
★利润问题常见关系式
基本关系:(1)利润=售价-________;
(3)总利润=____________×销量.
进价
单个利润
效果评价、归纳总结
1.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后会有81台电脑被感染,每轮感染中平均一台电脑会感染几台电脑?设每轮感染中平均一台电脑会感染x台电脑,则x满足的方程是( )
A.1+x2=81 B.(1+x)2=81
C.1+x+x2=81 D.1+x+(1+x)2=81
2.新年里,一个小组有若干人,若每人给小组的其他成员赠送一张贺年卡,则全组送贺卡共72张,此小组人数为( )
A.7 B.8 C.9 D.10
C
B
效果评价、归纳总结
3.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查表明,这种台灯的售价每上涨1元,某销售量就将减少10台,为了实现平均每月10000元销售利润,这种台灯的售价应定为多少?这时应进台灯多少台?
解:设台灯的售价因定为 x 元.根据题意,得
(x - 30)[600 - 10 (x - 40) ] =10000.
整理,得 x2 - 130x + 4000 = 0 .
解得 x1 = 50 , x2= 80.
当x = 50 时 , 应进台灯600- 10(50 - 40)=500 (台).
当x = 80 时 , 应进台灯600- 10(80 - 40)=200 (台).
效果评价、归纳总结
5.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,问有多少家公司出席了这次交易会?
4.一条直线上有n个点,共形成了45条线段,求n的值.
效果评价、归纳总结
6.菜农李伟种植的某蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该蔬菜滞销,李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:方案一:打九折销售;方案二:不打折,每吨优惠现金200元.试问小华选择哪种方案更优惠?请说明理由.
效果评价、归纳总结
解:(1)设平均每次下调的百分率为x. 由题意,得
5(1-x)2=3.2,
解得 x1=20%,x2=1.8 (舍去)
∴平均每次下调的百分率为20%.
(2)小华选择方案一购买更优惠,理由如下:
方案一所需费用为3.2×0.9×5000=14400(元);
方案二所需费用为3.2×5000-200×5=15000(元).
∵14400<15000,
∴小华选择方案一购买更优惠.
效果评价、归纳总结
1.单循环赛问题中的等量关系:
比赛总场数=x(x-1)÷2(x为球队个数).
易错点是列方程时忽略除以2.
2.利润问题中的等量关系:
利润= (售价-进价)×销售量.
3.解决较为复杂的应用题时,要认真读懂题意,正确找到等量关系并准确表达,建立方程模型,并检验解出的根是否符合题意.
效果评价、归纳总结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
