冀教版(2024)九年级数学上册 24.2 解一元二次方程 课件(18张PPT)
文档属性
| 名称 | 冀教版(2024)九年级数学上册 24.2 解一元二次方程 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
24.2解一元二次方程
冀教版九上
第二十四章 一元二次方程
新课引入
新课学习
典例精析
测试小结
第三课时 因式分解法
x2=7x
请你解出这个方程,然后与同伴交流,大家的解法都一样吗?如果不一样,谁的解法更快捷呢?
夯实基础 巩固提升
03 会灵活选择合适的方法解一元二次方程.
02 会熟练运用因式分解法解一元二次方程.
01理解用因式分解法解一元二次方程的合理性.
学习目标
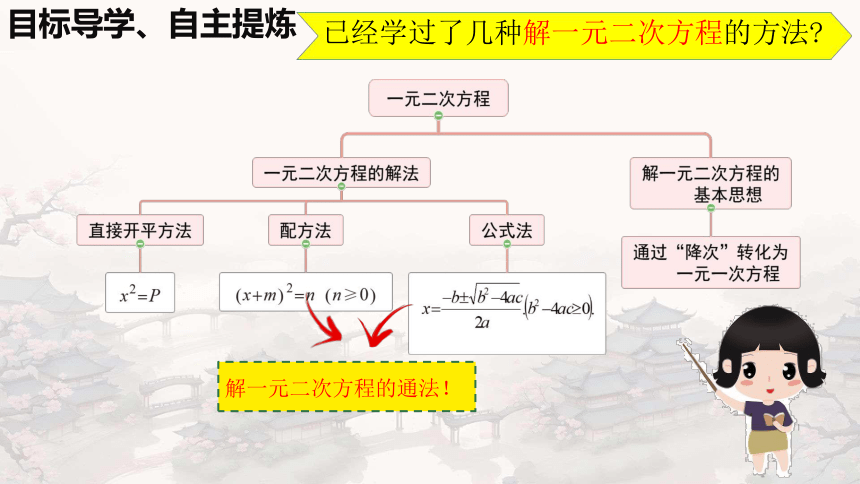
目标导学、自主提炼
已经学过了几种解一元二次方程的方法
解一元二次方程的通法!
目标导学、自主提炼
x2=7x
请你解出这个方程,然后与同伴交流,大家的解法都一样吗?如果不一样,谁的解法更快捷呢?
目标导学、自主提炼
公式法
配方法
目标导学、自主提炼
方法三:将方程x2=7x
移项得,x2-7x=0
方程左边分解因式,得x(x-7)=0
两因式相乘得0,则每一项都有可能为0
∴x=0,或x-7=0
解得x=0或x=7
哪种解方程的方法做起来最快捷?你喜欢哪一种解法?为什么?
方法三
因为计算量最小
这种方法是今天我们要学习的因式分解法
目标导学、自主提炼
像这样,先把一元二次方程右边化为0,再把左边因式分解为两个一次因式的乘积的形式,进而转化为两个一元一次方程,从而求出方程的根,这种解一元二次方程的方法叫做因式分解法.
转化思想
特别提醒:
1、用因式分解法解一元二次方程的条件:方程右边等于0,左边易于分解。
2、理论依据:如果两个因式的积等于零,那么至少有一个因式等于零。
3、关键是熟练掌握因式分解的知识。
简记歌诀:
右化零 左分解
两因式 各求解
目标导学、自主提炼
把下列多项式因式分解
(2)3m -6m+3
(1)
(4)
(3)(2x-3) -16
合作探究、展示点评
用因式分解法解一元二次方程
方程两边不能同时除以含未知数的式子!
(容易造成丟解现象!)
错误的原因是什么?如何避免?
合作探究、展示点评
因式分解法解一元二次方程的一般步骤:
(1)整理方程,使其右边为0;
(2)将方程左边分解为两个一次式的乘积形式;
(3)分别令每个一次式为0,得到两个一元一次方程;
(4)分别解这两个一元一次方程,它们的解就是原方
程的解.
合作探究、展示点评
因式分解法,只适合一些特殊的一元二次方程.即当把方程的所有项移到等号左边的时候,方程的左边可以分解因式.并不是所有的一元二次方程都能用因式分解法去解.
思考:任何方程都可以用因式分解法解吗?
合作探究、展示点评
先选择合适的解法,再解方程.
① x2+2x=3
② x2-3x=5(x-3)
③ 3x2-2x-2=0
④(3x+2)2=25
直接开平方法
配方法
公式法
因式分解法
思考:解一元二次方程如何选择适当的解法?与你的同伴交流一下吧.
合作探究、展示点评
选择适当的解法解一元二次方程
因式分解法
把等号的右边化为0后,左边可以分解因式.如:方程 x2-3x=5(x-3)
直接开平方法
等号左边为平方形式,右边为一个非负数.如:方程(3x+2)2=25
配方法
所有方程均可,有时候计算量会大一些。
公式法
不能用其他方法时,化为一般形式用.如:方程3x2-2x-2=0
ax2+bx+c=0(a ≠0)
效果评价 归纳总结
合作探究、展示点评
会选用恰当的方法解一元二次方程.
效果评价 归纳总结
1.用适当的方法解下列方程:
(1)(x+1)2=9
(2)x2-4x=6
(3)2x2-3x-1=0
(4)(x-1)2=(2x+1)2
直接开平方或因式分解
配方法
公式法
直接开平方或因式分解
效果评价、归纳总结
2.已知3是关于想的方程x2-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边的长,则△ABC的周长为( )
10或11
效果评价、归纳总结
24.2解一元二次方程
冀教版九上
第二十四章 一元二次方程
新课引入
新课学习
典例精析
测试小结
第三课时 因式分解法
x2=7x
请你解出这个方程,然后与同伴交流,大家的解法都一样吗?如果不一样,谁的解法更快捷呢?
夯实基础 巩固提升
03 会灵活选择合适的方法解一元二次方程.
02 会熟练运用因式分解法解一元二次方程.
01理解用因式分解法解一元二次方程的合理性.
学习目标
目标导学、自主提炼
已经学过了几种解一元二次方程的方法
解一元二次方程的通法!
目标导学、自主提炼
x2=7x
请你解出这个方程,然后与同伴交流,大家的解法都一样吗?如果不一样,谁的解法更快捷呢?
目标导学、自主提炼
公式法
配方法
目标导学、自主提炼
方法三:将方程x2=7x
移项得,x2-7x=0
方程左边分解因式,得x(x-7)=0
两因式相乘得0,则每一项都有可能为0
∴x=0,或x-7=0
解得x=0或x=7
哪种解方程的方法做起来最快捷?你喜欢哪一种解法?为什么?
方法三
因为计算量最小
这种方法是今天我们要学习的因式分解法
目标导学、自主提炼
像这样,先把一元二次方程右边化为0,再把左边因式分解为两个一次因式的乘积的形式,进而转化为两个一元一次方程,从而求出方程的根,这种解一元二次方程的方法叫做因式分解法.
转化思想
特别提醒:
1、用因式分解法解一元二次方程的条件:方程右边等于0,左边易于分解。
2、理论依据:如果两个因式的积等于零,那么至少有一个因式等于零。
3、关键是熟练掌握因式分解的知识。
简记歌诀:
右化零 左分解
两因式 各求解
目标导学、自主提炼
把下列多项式因式分解
(2)3m -6m+3
(1)
(4)
(3)(2x-3) -16
合作探究、展示点评
用因式分解法解一元二次方程
方程两边不能同时除以含未知数的式子!
(容易造成丟解现象!)
错误的原因是什么?如何避免?
合作探究、展示点评
因式分解法解一元二次方程的一般步骤:
(1)整理方程,使其右边为0;
(2)将方程左边分解为两个一次式的乘积形式;
(3)分别令每个一次式为0,得到两个一元一次方程;
(4)分别解这两个一元一次方程,它们的解就是原方
程的解.
合作探究、展示点评
因式分解法,只适合一些特殊的一元二次方程.即当把方程的所有项移到等号左边的时候,方程的左边可以分解因式.并不是所有的一元二次方程都能用因式分解法去解.
思考:任何方程都可以用因式分解法解吗?
合作探究、展示点评
先选择合适的解法,再解方程.
① x2+2x=3
② x2-3x=5(x-3)
③ 3x2-2x-2=0
④(3x+2)2=25
直接开平方法
配方法
公式法
因式分解法
思考:解一元二次方程如何选择适当的解法?与你的同伴交流一下吧.
合作探究、展示点评
选择适当的解法解一元二次方程
因式分解法
把等号的右边化为0后,左边可以分解因式.如:方程 x2-3x=5(x-3)
直接开平方法
等号左边为平方形式,右边为一个非负数.如:方程(3x+2)2=25
配方法
所有方程均可,有时候计算量会大一些。
公式法
不能用其他方法时,化为一般形式用.如:方程3x2-2x-2=0
ax2+bx+c=0(a ≠0)
效果评价 归纳总结
合作探究、展示点评
会选用恰当的方法解一元二次方程.
效果评价 归纳总结
1.用适当的方法解下列方程:
(1)(x+1)2=9
(2)x2-4x=6
(3)2x2-3x-1=0
(4)(x-1)2=(2x+1)2
直接开平方或因式分解
配方法
公式法
直接开平方或因式分解
效果评价、归纳总结
2.已知3是关于想的方程x2-(m+1)x+2m=0的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC的两条边的长,则△ABC的周长为( )
10或11
效果评价、归纳总结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
