人教版高中物理必修第一册第三章相互作用——力3.5共点力的平衡课件(20页ppt)
文档属性
| 名称 | 人教版高中物理必修第一册第三章相互作用——力3.5共点力的平衡课件(20页ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-24 08:53:24 | ||
图片预览






文档简介
(共20张PPT)
第三章 相互作用——力
第5节 共点力的平衡
思考:什么叫平衡状态?在日常生活中我们看过哪些平衡现象?
1.理解共点力和共点力平衡的概念,知道共点力作用下物体平衡的条件。
2.会用共点力平衡条件解决有关力的平衡问题,会用正交分解法解决相关问题。
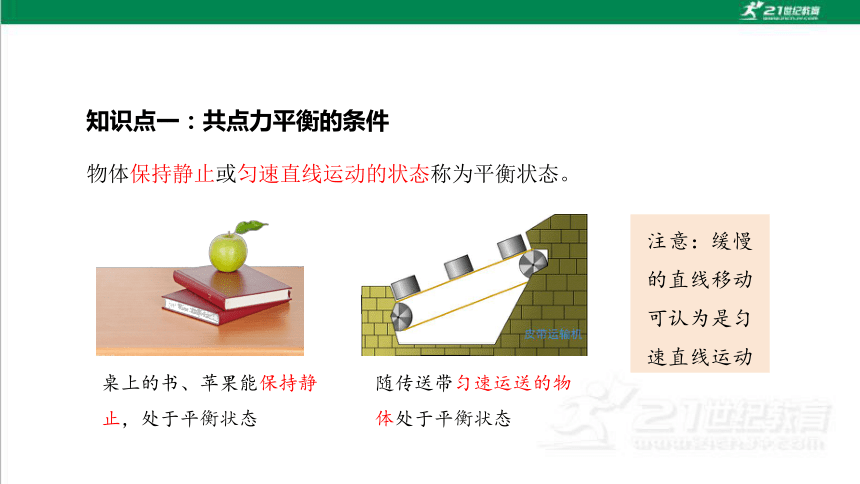
物体保持静止或匀速直线运动的状态称为平衡状态。
随传送带匀速运送的物体处于平衡状态
桌上的书、苹果能保持静止,处于平衡状态
知识点一:共点力平衡的条件
注意:缓慢的直线移动可认为是匀速直线运动
共点力作用下物体的平衡条件是合力为零,即F合=0。
物体受两个力作用而平衡
两个力一定等大反向且作用在一条直线上
物体受三个以上的共点力而平衡
等效简化为两个共点力而平衡
二力平衡时物体合力为0
1.平衡状态
物体保持静止或匀速直线运动的状态。
2.平衡条件
合力为零
①二力平衡:两个力必定等大反向,在同一条直线上。
②三力平衡:任意两个力的合力与第三个力等大反向。
③N个力平衡:任意一个力与剩余(N-1)个力的合力一定等大反向。
知识点二:物体平衡条件的应用
1.合成法:物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力大小相等、方向相反。
2.分解法:物体在三个共点力作用下处于平衡状态时,将某个力按作用效果分解,则其分力与其他两个力分别平衡。
3.正交分解法:物体在多个共点力作用下处于平衡状态,应用正交分解法,则有:∑Fx=F1x+F2x+F3x+…+Fnx=0,
∑Fy=F1y+F2y+F3y+…+Fny=0
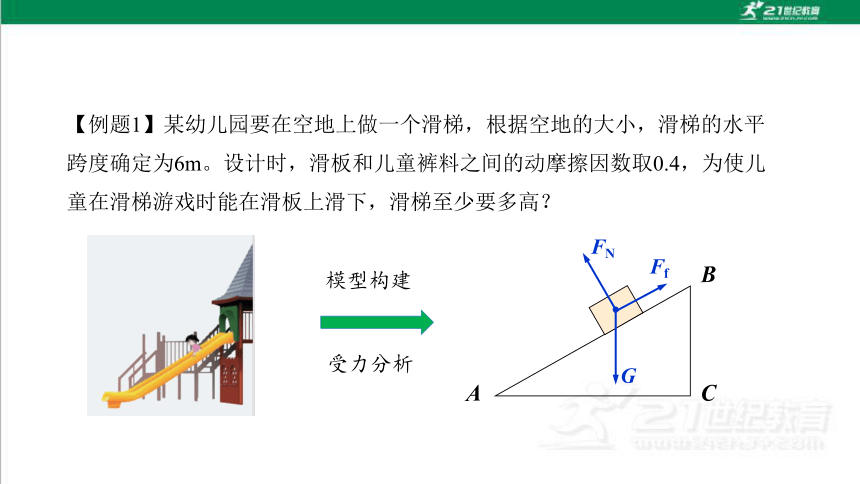
【例题1】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
A
B
C
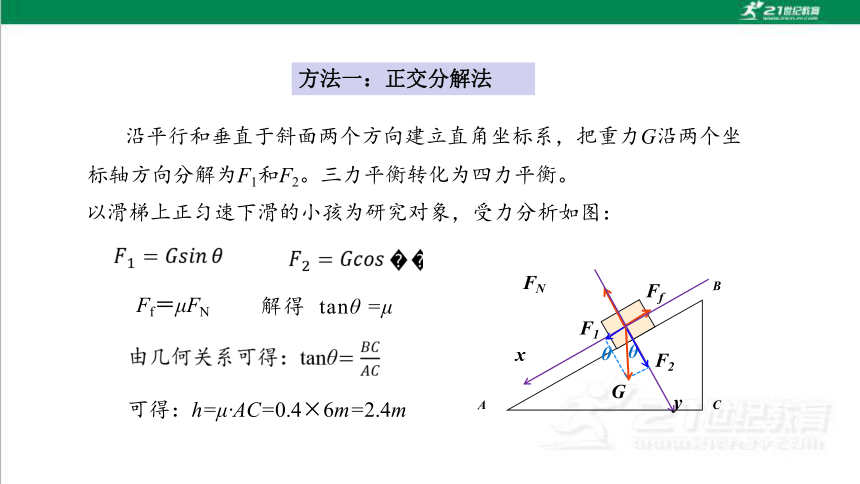
方法一:正交分解法
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
F1
F2
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等值反向
方法二:合成法
G
G’
A
B
C
θ
θ
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
Ff
FN
4.共点力平衡问题的解题思路
(1)明确研究对象(物体、质点或绳的结点等)。
(2)分析研究对象所处的运动状态,判定其是否处于平衡状态。
(3)对研究对象进行受力分析,并画出受力示意图。
(4)列平衡方程,应用共点力平衡的条件,选择恰当的方法(合成法、分解法、正交分解法)列出平衡方程。
(5)求解方程,并讨论结果。
【例题2】“风力仪”可直接测量风力的大小,其原理如图所示。仪器中一根轻质金属丝悬挂着一个金属球。无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度。风力越大,偏角越大。通过传感器,就可以根据偏角的大小指示出风力大小。那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(重力加速度为g)
解法一:合成法
如图所示,风力F和拉力FT的合力与金属球所受的重力等大反向,由平行四边形定则可得F=mgtan θ。
解法二:分解法
重力有两个作用效果:使金属球抵抗风的吹力和使金属丝拉紧,可以将金属球所受的重力沿水平方向和金属丝的方向进行分解,如图所示,由几何关系可得F=F′=mgtan θ。
解法三:正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直方向为y轴,建立坐标系,如图所示。
由水平方向的合力Fx合和竖直方向的合力Fy合分别等于零,即:Fx合=FTsin θ-F=0 Fy合=FTcos θ-mg=0
解得F=mgtan θ。
1.若一个物体处于平衡状态,则此物体一定是( )
A.静止 B.匀速直线运动
C.速度为零 D.各共点力的合力为零
D
2.判一判
(1)处于平衡状态的物体一定处于静止状态。( )
(2)运动的物体合力不会为0。( )
(3)物体受两个力作用处于平衡状态,这两个力的合力一定为0。( )
(4)速度为0的物体一定处于平衡状态。( )
(5)“复兴”号列车在平直铁路上以350 km/h高速行驶时处于平衡状态。( )
(6)合力保持恒定的物体处于平衡状态。( )
×
×
√
×
√
×
3.如图所示,水平横梁一端插在墙壁内,另一端装一小滑轮B。一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=20 kg的重物,∠CBA=30°,则滑轮受到绳子的作用力大小为(g取10 N/kg)( )
C
4.如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
共点力的平衡
合力为0
平衡状态
共点力作用下物体平衡条件
共点力平衡条件的应用
合成法、分解法、正交分解法
静止或匀速直线运动的状态
第三章 相互作用——力
第5节 共点力的平衡
思考:什么叫平衡状态?在日常生活中我们看过哪些平衡现象?
1.理解共点力和共点力平衡的概念,知道共点力作用下物体平衡的条件。
2.会用共点力平衡条件解决有关力的平衡问题,会用正交分解法解决相关问题。
物体保持静止或匀速直线运动的状态称为平衡状态。
随传送带匀速运送的物体处于平衡状态
桌上的书、苹果能保持静止,处于平衡状态
知识点一:共点力平衡的条件
注意:缓慢的直线移动可认为是匀速直线运动
共点力作用下物体的平衡条件是合力为零,即F合=0。
物体受两个力作用而平衡
两个力一定等大反向且作用在一条直线上
物体受三个以上的共点力而平衡
等效简化为两个共点力而平衡
二力平衡时物体合力为0
1.平衡状态
物体保持静止或匀速直线运动的状态。
2.平衡条件
合力为零
①二力平衡:两个力必定等大反向,在同一条直线上。
②三力平衡:任意两个力的合力与第三个力等大反向。
③N个力平衡:任意一个力与剩余(N-1)个力的合力一定等大反向。
知识点二:物体平衡条件的应用
1.合成法:物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力大小相等、方向相反。
2.分解法:物体在三个共点力作用下处于平衡状态时,将某个力按作用效果分解,则其分力与其他两个力分别平衡。
3.正交分解法:物体在多个共点力作用下处于平衡状态,应用正交分解法,则有:∑Fx=F1x+F2x+F3x+…+Fnx=0,
∑Fy=F1y+F2y+F3y+…+Fny=0
【例题1】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
A
B
C
方法一:正交分解法
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
F1
F2
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等值反向
方法二:合成法
G
G’
A
B
C
θ
θ
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
Ff
FN
4.共点力平衡问题的解题思路
(1)明确研究对象(物体、质点或绳的结点等)。
(2)分析研究对象所处的运动状态,判定其是否处于平衡状态。
(3)对研究对象进行受力分析,并画出受力示意图。
(4)列平衡方程,应用共点力平衡的条件,选择恰当的方法(合成法、分解法、正交分解法)列出平衡方程。
(5)求解方程,并讨论结果。
【例题2】“风力仪”可直接测量风力的大小,其原理如图所示。仪器中一根轻质金属丝悬挂着一个金属球。无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度。风力越大,偏角越大。通过传感器,就可以根据偏角的大小指示出风力大小。那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?(重力加速度为g)
解法一:合成法
如图所示,风力F和拉力FT的合力与金属球所受的重力等大反向,由平行四边形定则可得F=mgtan θ。
解法二:分解法
重力有两个作用效果:使金属球抵抗风的吹力和使金属丝拉紧,可以将金属球所受的重力沿水平方向和金属丝的方向进行分解,如图所示,由几何关系可得F=F′=mgtan θ。
解法三:正交分解法
以金属球为坐标原点,取水平方向为x轴,竖直方向为y轴,建立坐标系,如图所示。
由水平方向的合力Fx合和竖直方向的合力Fy合分别等于零,即:Fx合=FTsin θ-F=0 Fy合=FTcos θ-mg=0
解得F=mgtan θ。
1.若一个物体处于平衡状态,则此物体一定是( )
A.静止 B.匀速直线运动
C.速度为零 D.各共点力的合力为零
D
2.判一判
(1)处于平衡状态的物体一定处于静止状态。( )
(2)运动的物体合力不会为0。( )
(3)物体受两个力作用处于平衡状态,这两个力的合力一定为0。( )
(4)速度为0的物体一定处于平衡状态。( )
(5)“复兴”号列车在平直铁路上以350 km/h高速行驶时处于平衡状态。( )
(6)合力保持恒定的物体处于平衡状态。( )
×
×
√
×
√
×
3.如图所示,水平横梁一端插在墙壁内,另一端装一小滑轮B。一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=20 kg的重物,∠CBA=30°,则滑轮受到绳子的作用力大小为(g取10 N/kg)( )
C
4.如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
共点力的平衡
合力为0
平衡状态
共点力作用下物体平衡条件
共点力平衡条件的应用
合成法、分解法、正交分解法
静止或匀速直线运动的状态
