广东省汕尾市2024-2025学年八年级下学期期末考试数学试卷(含详解)
文档属性
| 名称 | 广东省汕尾市2024-2025学年八年级下学期期末考试数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:28:23 | ||
图片预览



文档简介
广东省汕尾市2024-2025学年八年级下学期期末监测数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数中,自变量的取值范围是( )
A. B. C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A.1,1,2 B.1,2,3 C.1,1, D.2,3,4
3.下列计算错误的是( ).
A. B.
C. D.
4.年月日,神舟二十号载人飞船发射取得圆满成功,是中国载人航天在“东方红一号”发射55载之际开启的第次神舟问天之旅.为了培养青少年对航天知识学习的兴趣,某校开展航天知识竞赛活动.经过几轮筛选,八()班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛.经统计,四名同学成绩的平均数(单位:分)及方差如下表所示.要选一名成绩好且状态稳定的同学参赛,应选择( )
甲 乙 丙 丁
平均数
方差
A.甲 B.乙 C.丙 D.丁
5.汕尾城区“网红打卡景点”——小岛渔村(屿仔岛),为便于市民、游客通行,物流交往,现已在小岛与湖滨大道码头之间修建一座桥(如图),在与方向成角的方向上的点处测得,,则的长为( )
A. B. C. D.
6.对于函数,下列说法正确的是( )
A.它的图象经过二、三、四象限 B.y随x增大而减小
C.它的图象经过点 D.它的图象与y轴的交点为
7.如图,在中,D,E,F分别是的中点.若,则四边形的周长是( )
A.7 B.10 C.14 D.18
8.如图,直线:与直线:在同一平面直角坐标系内交于点,有下列结论:;;当时,;关于,的方程组的解是.其中结论正确的个数是( )
A. B. C. D.
9.如图,矩形内有两个相邻的正方形(空白部分),其面积分别为2和8,则图中阴影部分的面积为( )
A.2 B. C.6 D.12
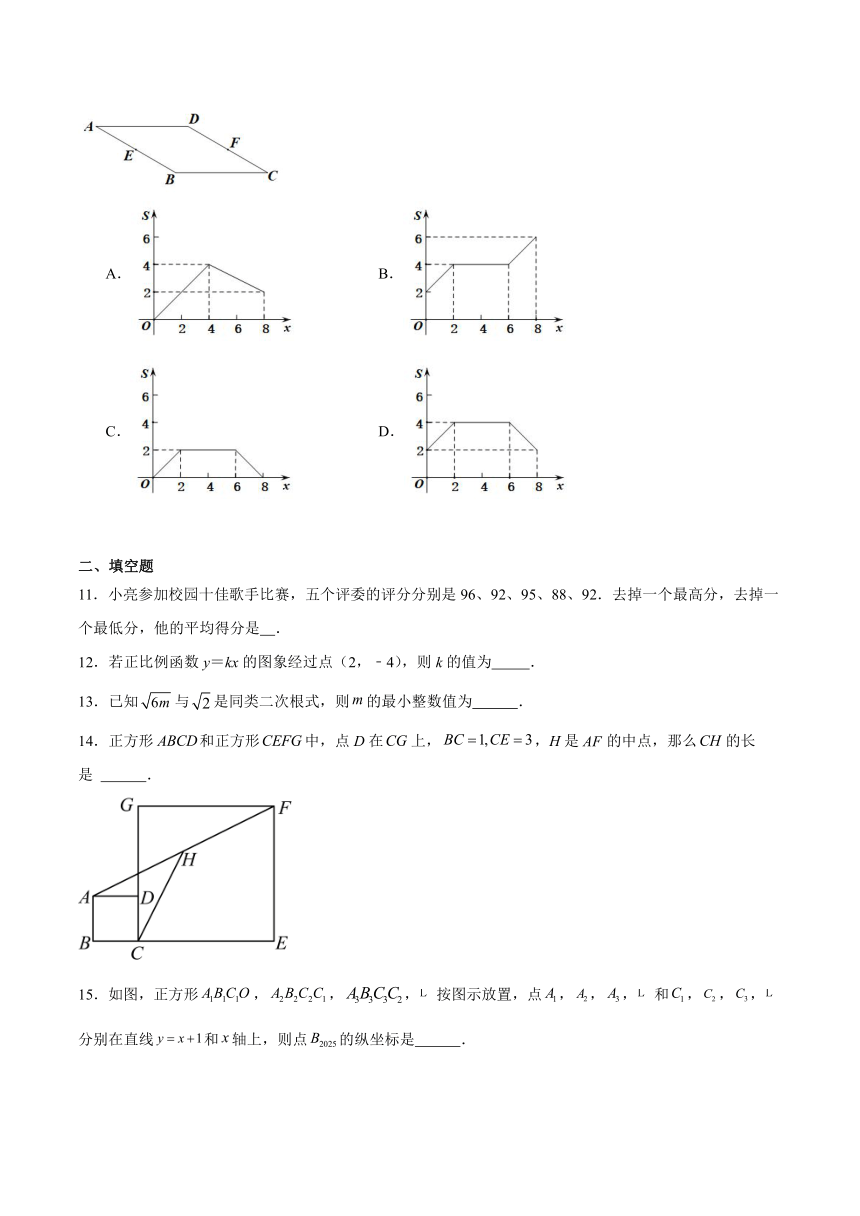
10.如图,菱形ABCD中,,,点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ).
A. B.
C. D.
二、填空题
11.小亮参加校园十佳歌手比赛,五个评委的评分分别是96、92、95、88、92.去掉一个最高分,去掉一个最低分,他的平均得分是 .
12.若正比例函数y=kx的图象经过点(2,﹣4),则k的值为 .
13.已知与是同类二次根式,则的最小整数值为 .
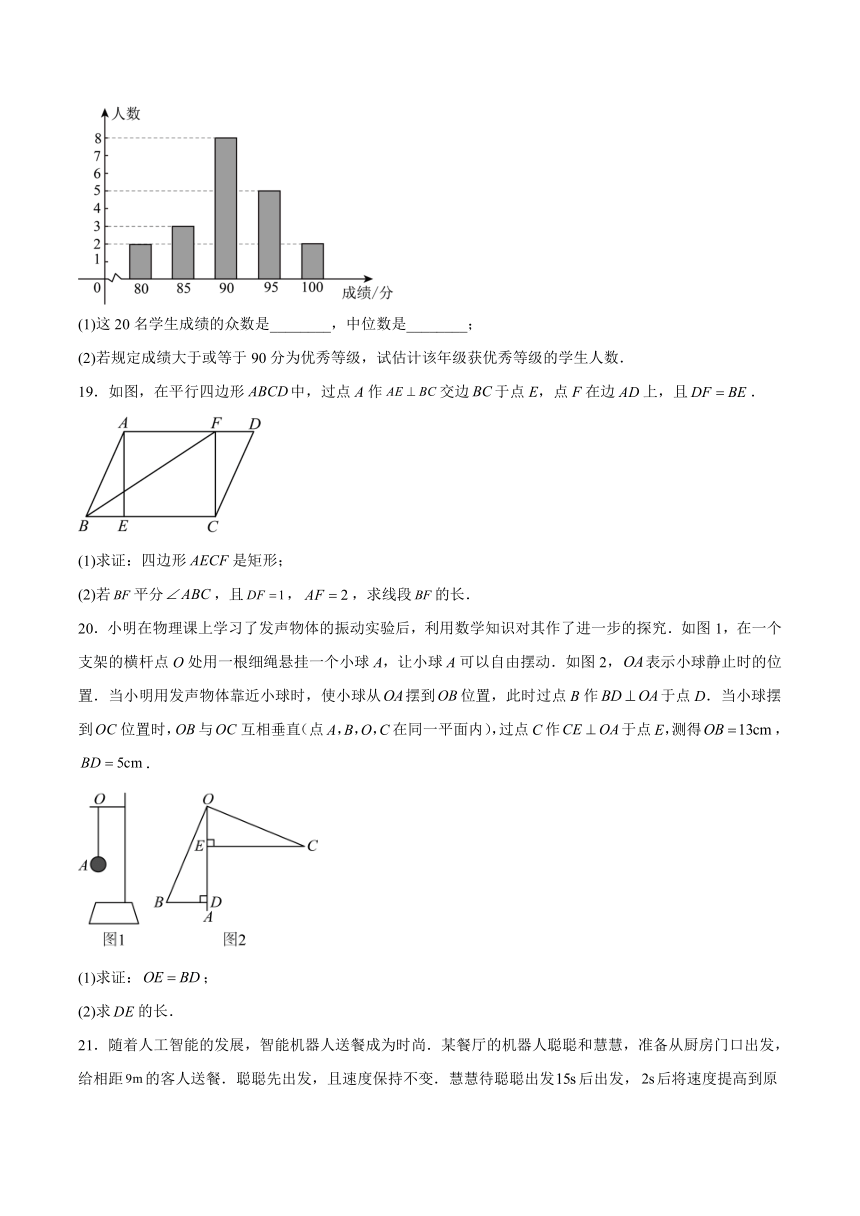
14.正方形和正方形中,点D在上,,H是的中点,那么的长是 .
15.如图,正方形,,,按图示放置,点,,,和,,,分别在直线和轴上,则点的纵坐标是 .
三、解答题
16.计算:.
17.已知:如图,在中,.求作:矩形ABCD.
作法:①作线段AB的垂直平分线交AB于点O.
②作射线CO.
③以点O为圆心,线段CO长为半径画弧,交射线CO于点D.
④连接AD,BD,则四边形ACBD即为所求作的矩形.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵,①
∴四边形ACBD是平行四边形.(②)(填推理的依据)
∵,
∴四边形ACBD是矩形.(③)(填推理的依据)
18.汕尾作为第十五届全运会帆船赛事承办地,各级各单位以“喜迎十五运”为主线,精心策划系列活动,掀起全民参与热潮.某中学九年级举办“体育+文旅”知识问答活动.用简单随机抽样的方法,从该年级全体400名学生中抽取20名,并将答题成绩(百分制)绘制成条形统计图.
(1)这20名学生成绩的众数是________,中位数是________;
(2)若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.
19.如图,在平行四边形中,过点A作交边于点E,点F在边上,且.
(1)求证:四边形是矩形;
(2)若平分,且,,求线段的长.
20.小明在物理课上学习了发声物体的振动实验后,利用数学知识对其作了进一步的探究.如图1,在一个支架的横杆点O处用一根细绳悬挂一个小球A,让小球A可以自由摆动.如图2,表示小球静止时的位置.当小明用发声物体靠近小球时,使小球从摆到位置,此时过点B作于点D.当小球摆到位置时,与互相垂直(点A,B,O,C在同一平面内),过点C作于点E,测得,.
(1)求证:;
(2)求的长.
21.随着人工智能的发展,智能机器人送餐成为时尚.某餐厅的机器人聪聪和慧慧,准备从厨房门口出发,给相距的客人送餐.聪聪先出发,且速度保持不变.慧慧待聪聪出发后出发,后将速度提高到原来的倍.设聪聪行走的时间为,聪聪和慧慧行走的路程分别为 .,与x之间的函数图象如图所示.
(1)求慧慧提速后的速度;
(2)求图中的与的值.
22.【问题原型】如图①,在正方形中,点E,F分别在边,上,且,点P为,的交点,则________;
【探究发现】某数学兴趣小组尝试对上述问题进行变式,转换了问题的背景图形,如图②,在等边三角形中,点E,F分别在边,上(不与三角形顶点重合),且,点P为,的交点,请将图形补充完整,并求的度数;
【拓展提升】利用“探究发现”的思路及结论,继续探究,尝试解决如下问题:如图③,在菱形中,,点E,F分别在边,上,且,,点P为,的交点,求的度数.
23.如图,在平面直角坐标系中,O为坐标原点,矩形的顶点,,将矩形的一个角沿直线折叠,使得点落在对角线上的点E处,折痕与x轴交于点D.
(1)线段的长度___________;
(2)求直线所对应的函数表达式;
(3)若点Q在线段上,在线段上是否存在点P,使以D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
广东省汕尾市2024-2025学年八年级下学期期末监测数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A D C D A A D
1.B
【详解】函数中,被开方数必须满足非负条件,即:
解得:
,
因此,自变量的取值范围是,
故选:B.
2.C
【详解】解:A、∵,∴此三条线段不能构成直角三角形,故不符合题意;
B、∵,∴此三条线段不能构成直角三角形,故不符合题意;
C、∵,∴此三条线段不能构成直角三角形,故不符合题意;
D、∵,∴此三条线段不能构成直角三角形,故不符合题意;
故选:C.
3.A
【详解】解:A、 3与不是同类二次根式,不能合并,故错误,符合题意;
B、 ,正确,不符合题意;
C、,正确,不符合题意;
D、,正确,不符合题意;
故选A.
4.A
【详解】解:∵甲和丙的平均分均为分,乙为分,丁为分,
∴甲和丙的成绩更优,
∵甲的方差为,丙的方差为,方差越小,成绩越稳定,
∴甲的状态更稳定,
故选:.
5.D
【详解】解:由题意得,
∴,
故选:.
6.C
【详解】解:A.∵,,∴它的图象经过一、三、四象限,原说法错误
B. ∵,∴y随x增大而增大,原说法错误
C. 当时,原说法正确
D. 当时,原说法错误
故选:C
7.D
【详解】解:D,E,F分别是,,的中点,,,
、分别是的中位线,,,
,且,,
四边形的周长为:.,
故选:D.
8.A
【详解】解:由图象可知,,,故正确;
由直线:与直线:在同一平面直角坐标系内交于点,可知的横坐标为,
∴当时,,故正确;
∵的横坐标为,且在直线:,
∴点,
∴关于,的方程组的解是,故正确,
综上可知:正确,共个,
故选:.
9.A
【详解】解:∵矩形内有两个相邻的正方形(空白部分),其面积分别为2和8,
∴大正方形的边长为,小正方形的边长为,
∴题图中阴影部分的面积为.
故选:A.
10.D
【详解】解:在菱形ABCD中:,
∵点E,F分别是边AB,CD的中点,
∴.
当P在EB上时, 时,过点P作PH⊥AD于点H,则,,
∵∠A=30°,
∴,
∴,
∴此时图象是与y轴交于 的线段;
当P在BC上时, 时,过点B作BM⊥AD于点M,则,
∵∠A=30°,
∴,
∴,
∵,
∴,
∴此时图象是平行于x轴的线段;
当P在CF上时, 时,过点P作PN⊥AD于点N,则,,
∴,
∵∠A=30°,,
∴ ,
∴,
∴S=,
∴此时图象是一条过 的线段;
观察四个选项,只有选项D符合题意,
故选:D.
11.93分
【详解】解:去掉一个最高分96,去掉一个最低分88,他的平均得分是分,
故答案为:93分.
12.-2
【详解】解:∵正比例函数y=kx的图象经过点(2,﹣4),
∴﹣4=2k,
解得:k=﹣2.
故答案为:﹣2.
13.3
【详解】解:∵与是同类二次根式,
∴,
∴的最小整数值为3,
故答案为:3.
14.
【详解】解:如图,连接,
∵正方形和正方形中,,
∴,,,
∴,
由勾股定理得,,
∵H是的中点,
∴,
故答案为:.
15.
【详解】解:当时,,
点的坐标为.
为正方形,
点的坐标为,点的坐标为.
同理,可得:,,,
点的坐标为,
点的纵坐标为,
点的纵坐标为.
故答案为:.
16.
【详解】解:原式
.
17.(1)见解析
(2)①OC ②对角线互相平分的四边形是平行四边形 ③有一个角是直角的平行四边形是矩形
【详解】(1)解:作图如图所示.
(2)证明∶∵OA=OB, OC=OD,
∴四边形ACBD是平行四边形(对角线互相平分的四边形是平行四边形),
∵∠ACB=90°,
∴四边形ACBD是矩形(有一个角是直角的平行四边形是矩形).
故答案为∶①OC ②对角线互相平分的四边形是平行四边形 ③有一个角是直角的平行四边形是矩形.
18.(1)90分,90分
(2)300人
【详解】(1)解:由统计图中90分对应的人数最多,因此这组数据的众数应该是90分,
由于人数总和是20人为偶数,将数据从小到大排列后,第10个和第11个数据都是90分,因此这组数据的中位数应该是90分,
故答案为:90分,90分;
(2)解:根据题意得:(人),
答:估计该年级获优秀等级的学生人数是300人.
19.(1)见解析
(2)
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形;
(2)解:∵平分,,
∴,
∴,,
在中,,
,
在中,.
20.(1)见解析
(2)
【详解】(1)证明:∵,
∴,
又∵,,
∴,
∴,
∴,
在和中,
,
∴,
∴;
(2)解:在中, ,
由(1)得,
∴.
21.(1)
(2),
【详解】(1)解:由图像可得,慧慧从走到了时,总共用了,
故提速前的速度为,
∵慧慧提速后将速度提高到原来的倍,
∴慧慧提速后的速度为,
(2)解:由图象可得线段的过程中,慧慧从处行走到了,
由(1)可得慧慧在线段的过程中的速度为,
∴慧慧在线段的过程中所用的时间为,
∴的值为,
结合图像可得点坐标为,
即聪聪从处行走到了时,用了,
∴慧慧的速度为,
∴慧慧行走用的时间为,
即,
故,.
22.【问题原型】;【探究发现】图见解析,;【拓展提升】.
【详解】解:(1)四边形是正方形
∴,.
∵,
∴,
∴,
∵,
∴,
∴;
(2)探究发现,如图()中
∵是等边三角形,
∴,,
在和中,
∴,
∴,
∵,
∴,
(3)拓展提升:如图③中,连接交于.
四边形是菱形,
∴,,,,
∵,
∴,
∴是等边三角形,
∵,,
∴,
∴,
∵,
∴,
∵是等边三角形,
由()可知,.
23.(1)10
(2)
(3)存在,
【详解】(1)解:由题意,得:点的坐标为,,,
,
故答案为:10.
(2)设,则,,
,即,
,
,
点的坐标为.
设直线所对应的函数表达式为,
将,代入,得:
,
解得:,
直线所对应的函数表达式为;
(3)存在,理由:过点作轴于点,如图所示.
,
,
,
在中,,
点的坐标为,
由,设直线的解析式为:,
把代入得:,解得:,
直线的解析式为:,
令,则,解得:,
存在,点的坐标为:.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数中,自变量的取值范围是( )
A. B. C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A.1,1,2 B.1,2,3 C.1,1, D.2,3,4
3.下列计算错误的是( ).
A. B.
C. D.
4.年月日,神舟二十号载人飞船发射取得圆满成功,是中国载人航天在“东方红一号”发射55载之际开启的第次神舟问天之旅.为了培养青少年对航天知识学习的兴趣,某校开展航天知识竞赛活动.经过几轮筛选,八()班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛.经统计,四名同学成绩的平均数(单位:分)及方差如下表所示.要选一名成绩好且状态稳定的同学参赛,应选择( )
甲 乙 丙 丁
平均数
方差
A.甲 B.乙 C.丙 D.丁
5.汕尾城区“网红打卡景点”——小岛渔村(屿仔岛),为便于市民、游客通行,物流交往,现已在小岛与湖滨大道码头之间修建一座桥(如图),在与方向成角的方向上的点处测得,,则的长为( )
A. B. C. D.
6.对于函数,下列说法正确的是( )
A.它的图象经过二、三、四象限 B.y随x增大而减小
C.它的图象经过点 D.它的图象与y轴的交点为
7.如图,在中,D,E,F分别是的中点.若,则四边形的周长是( )
A.7 B.10 C.14 D.18
8.如图,直线:与直线:在同一平面直角坐标系内交于点,有下列结论:;;当时,;关于,的方程组的解是.其中结论正确的个数是( )
A. B. C. D.
9.如图,矩形内有两个相邻的正方形(空白部分),其面积分别为2和8,则图中阴影部分的面积为( )
A.2 B. C.6 D.12
10.如图,菱形ABCD中,,,点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ).
A. B.
C. D.
二、填空题
11.小亮参加校园十佳歌手比赛,五个评委的评分分别是96、92、95、88、92.去掉一个最高分,去掉一个最低分,他的平均得分是 .
12.若正比例函数y=kx的图象经过点(2,﹣4),则k的值为 .
13.已知与是同类二次根式,则的最小整数值为 .
14.正方形和正方形中,点D在上,,H是的中点,那么的长是 .
15.如图,正方形,,,按图示放置,点,,,和,,,分别在直线和轴上,则点的纵坐标是 .
三、解答题
16.计算:.
17.已知:如图,在中,.求作:矩形ABCD.
作法:①作线段AB的垂直平分线交AB于点O.
②作射线CO.
③以点O为圆心,线段CO长为半径画弧,交射线CO于点D.
④连接AD,BD,则四边形ACBD即为所求作的矩形.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵,①
∴四边形ACBD是平行四边形.(②)(填推理的依据)
∵,
∴四边形ACBD是矩形.(③)(填推理的依据)
18.汕尾作为第十五届全运会帆船赛事承办地,各级各单位以“喜迎十五运”为主线,精心策划系列活动,掀起全民参与热潮.某中学九年级举办“体育+文旅”知识问答活动.用简单随机抽样的方法,从该年级全体400名学生中抽取20名,并将答题成绩(百分制)绘制成条形统计图.
(1)这20名学生成绩的众数是________,中位数是________;
(2)若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.
19.如图,在平行四边形中,过点A作交边于点E,点F在边上,且.
(1)求证:四边形是矩形;
(2)若平分,且,,求线段的长.
20.小明在物理课上学习了发声物体的振动实验后,利用数学知识对其作了进一步的探究.如图1,在一个支架的横杆点O处用一根细绳悬挂一个小球A,让小球A可以自由摆动.如图2,表示小球静止时的位置.当小明用发声物体靠近小球时,使小球从摆到位置,此时过点B作于点D.当小球摆到位置时,与互相垂直(点A,B,O,C在同一平面内),过点C作于点E,测得,.
(1)求证:;
(2)求的长.
21.随着人工智能的发展,智能机器人送餐成为时尚.某餐厅的机器人聪聪和慧慧,准备从厨房门口出发,给相距的客人送餐.聪聪先出发,且速度保持不变.慧慧待聪聪出发后出发,后将速度提高到原来的倍.设聪聪行走的时间为,聪聪和慧慧行走的路程分别为 .,与x之间的函数图象如图所示.
(1)求慧慧提速后的速度;
(2)求图中的与的值.
22.【问题原型】如图①,在正方形中,点E,F分别在边,上,且,点P为,的交点,则________;
【探究发现】某数学兴趣小组尝试对上述问题进行变式,转换了问题的背景图形,如图②,在等边三角形中,点E,F分别在边,上(不与三角形顶点重合),且,点P为,的交点,请将图形补充完整,并求的度数;
【拓展提升】利用“探究发现”的思路及结论,继续探究,尝试解决如下问题:如图③,在菱形中,,点E,F分别在边,上,且,,点P为,的交点,求的度数.
23.如图,在平面直角坐标系中,O为坐标原点,矩形的顶点,,将矩形的一个角沿直线折叠,使得点落在对角线上的点E处,折痕与x轴交于点D.
(1)线段的长度___________;
(2)求直线所对应的函数表达式;
(3)若点Q在线段上,在线段上是否存在点P,使以D,E,P,Q为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
广东省汕尾市2024-2025学年八年级下学期期末监测数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A D C D A A D
1.B
【详解】函数中,被开方数必须满足非负条件,即:
解得:
,
因此,自变量的取值范围是,
故选:B.
2.C
【详解】解:A、∵,∴此三条线段不能构成直角三角形,故不符合题意;
B、∵,∴此三条线段不能构成直角三角形,故不符合题意;
C、∵,∴此三条线段不能构成直角三角形,故不符合题意;
D、∵,∴此三条线段不能构成直角三角形,故不符合题意;
故选:C.
3.A
【详解】解:A、 3与不是同类二次根式,不能合并,故错误,符合题意;
B、 ,正确,不符合题意;
C、,正确,不符合题意;
D、,正确,不符合题意;
故选A.
4.A
【详解】解:∵甲和丙的平均分均为分,乙为分,丁为分,
∴甲和丙的成绩更优,
∵甲的方差为,丙的方差为,方差越小,成绩越稳定,
∴甲的状态更稳定,
故选:.
5.D
【详解】解:由题意得,
∴,
故选:.
6.C
【详解】解:A.∵,,∴它的图象经过一、三、四象限,原说法错误
B. ∵,∴y随x增大而增大,原说法错误
C. 当时,原说法正确
D. 当时,原说法错误
故选:C
7.D
【详解】解:D,E,F分别是,,的中点,,,
、分别是的中位线,,,
,且,,
四边形的周长为:.,
故选:D.
8.A
【详解】解:由图象可知,,,故正确;
由直线:与直线:在同一平面直角坐标系内交于点,可知的横坐标为,
∴当时,,故正确;
∵的横坐标为,且在直线:,
∴点,
∴关于,的方程组的解是,故正确,
综上可知:正确,共个,
故选:.
9.A
【详解】解:∵矩形内有两个相邻的正方形(空白部分),其面积分别为2和8,
∴大正方形的边长为,小正方形的边长为,
∴题图中阴影部分的面积为.
故选:A.
10.D
【详解】解:在菱形ABCD中:,
∵点E,F分别是边AB,CD的中点,
∴.
当P在EB上时, 时,过点P作PH⊥AD于点H,则,,
∵∠A=30°,
∴,
∴,
∴此时图象是与y轴交于 的线段;
当P在BC上时, 时,过点B作BM⊥AD于点M,则,
∵∠A=30°,
∴,
∴,
∵,
∴,
∴此时图象是平行于x轴的线段;
当P在CF上时, 时,过点P作PN⊥AD于点N,则,,
∴,
∵∠A=30°,,
∴ ,
∴,
∴S=,
∴此时图象是一条过 的线段;
观察四个选项,只有选项D符合题意,
故选:D.
11.93分
【详解】解:去掉一个最高分96,去掉一个最低分88,他的平均得分是分,
故答案为:93分.
12.-2
【详解】解:∵正比例函数y=kx的图象经过点(2,﹣4),
∴﹣4=2k,
解得:k=﹣2.
故答案为:﹣2.
13.3
【详解】解:∵与是同类二次根式,
∴,
∴的最小整数值为3,
故答案为:3.
14.
【详解】解:如图,连接,
∵正方形和正方形中,,
∴,,,
∴,
由勾股定理得,,
∵H是的中点,
∴,
故答案为:.
15.
【详解】解:当时,,
点的坐标为.
为正方形,
点的坐标为,点的坐标为.
同理,可得:,,,
点的坐标为,
点的纵坐标为,
点的纵坐标为.
故答案为:.
16.
【详解】解:原式
.
17.(1)见解析
(2)①OC ②对角线互相平分的四边形是平行四边形 ③有一个角是直角的平行四边形是矩形
【详解】(1)解:作图如图所示.
(2)证明∶∵OA=OB, OC=OD,
∴四边形ACBD是平行四边形(对角线互相平分的四边形是平行四边形),
∵∠ACB=90°,
∴四边形ACBD是矩形(有一个角是直角的平行四边形是矩形).
故答案为∶①OC ②对角线互相平分的四边形是平行四边形 ③有一个角是直角的平行四边形是矩形.
18.(1)90分,90分
(2)300人
【详解】(1)解:由统计图中90分对应的人数最多,因此这组数据的众数应该是90分,
由于人数总和是20人为偶数,将数据从小到大排列后,第10个和第11个数据都是90分,因此这组数据的中位数应该是90分,
故答案为:90分,90分;
(2)解:根据题意得:(人),
答:估计该年级获优秀等级的学生人数是300人.
19.(1)见解析
(2)
【详解】(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形;
(2)解:∵平分,,
∴,
∴,,
在中,,
,
在中,.
20.(1)见解析
(2)
【详解】(1)证明:∵,
∴,
又∵,,
∴,
∴,
∴,
在和中,
,
∴,
∴;
(2)解:在中, ,
由(1)得,
∴.
21.(1)
(2),
【详解】(1)解:由图像可得,慧慧从走到了时,总共用了,
故提速前的速度为,
∵慧慧提速后将速度提高到原来的倍,
∴慧慧提速后的速度为,
(2)解:由图象可得线段的过程中,慧慧从处行走到了,
由(1)可得慧慧在线段的过程中的速度为,
∴慧慧在线段的过程中所用的时间为,
∴的值为,
结合图像可得点坐标为,
即聪聪从处行走到了时,用了,
∴慧慧的速度为,
∴慧慧行走用的时间为,
即,
故,.
22.【问题原型】;【探究发现】图见解析,;【拓展提升】.
【详解】解:(1)四边形是正方形
∴,.
∵,
∴,
∴,
∵,
∴,
∴;
(2)探究发现,如图()中
∵是等边三角形,
∴,,
在和中,
∴,
∴,
∵,
∴,
(3)拓展提升:如图③中,连接交于.
四边形是菱形,
∴,,,,
∵,
∴,
∴是等边三角形,
∵,,
∴,
∴,
∵,
∴,
∵是等边三角形,
由()可知,.
23.(1)10
(2)
(3)存在,
【详解】(1)解:由题意,得:点的坐标为,,,
,
故答案为:10.
(2)设,则,,
,即,
,
,
点的坐标为.
设直线所对应的函数表达式为,
将,代入,得:
,
解得:,
直线所对应的函数表达式为;
(3)存在,理由:过点作轴于点,如图所示.
,
,
,
在中,,
点的坐标为,
由,设直线的解析式为:,
把代入得:,解得:,
直线的解析式为:,
令,则,解得:,
存在,点的坐标为:.
同课章节目录
