高二直线、平面专题复习:距离(新人教A版必修2)
文档属性
| 名称 | 高二直线、平面专题复习:距离(新人教A版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 329.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-20 16:38:00 | ||
图片预览



文档简介
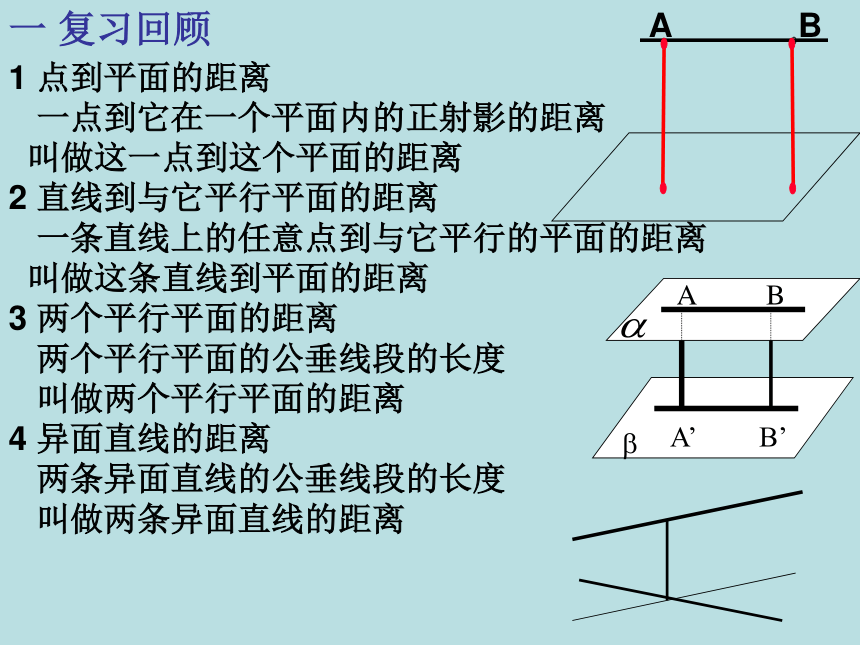
课件15张PPT。高二直线、平面专题复习 距离1 点到平面的距离
一点到它在一个平面内的正射影的距离
叫做这一点到这个平面的距离
2 直线到与它平行平面的距离
一条直线上的任意点到与它平行的平面的距离
叫做这条直线到平面的距离
3 两个平行平面的距离
两个平行平面的公垂线段的长度
叫做两个平行平面的距离
4 异面直线的距离
两条异面直线的公垂线段的长度
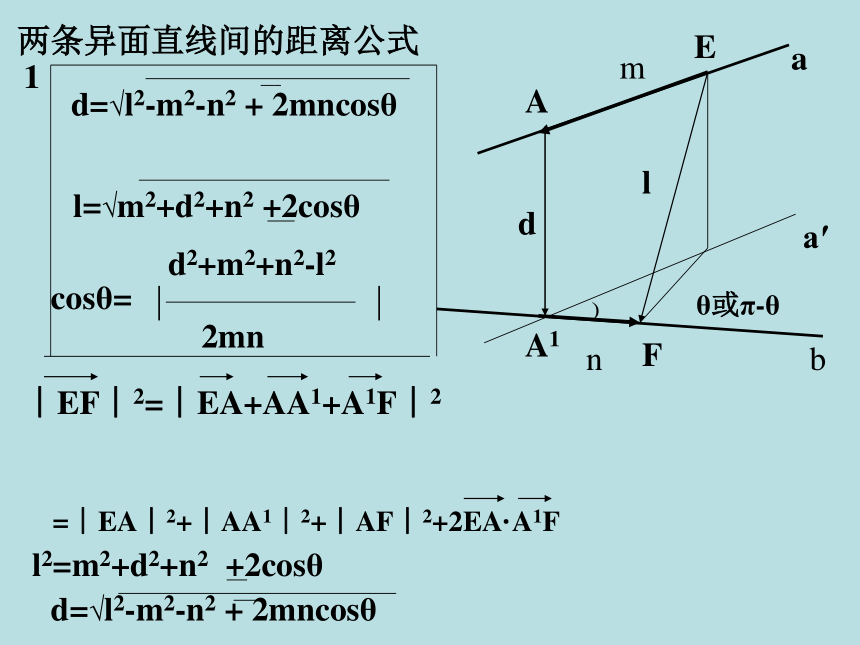
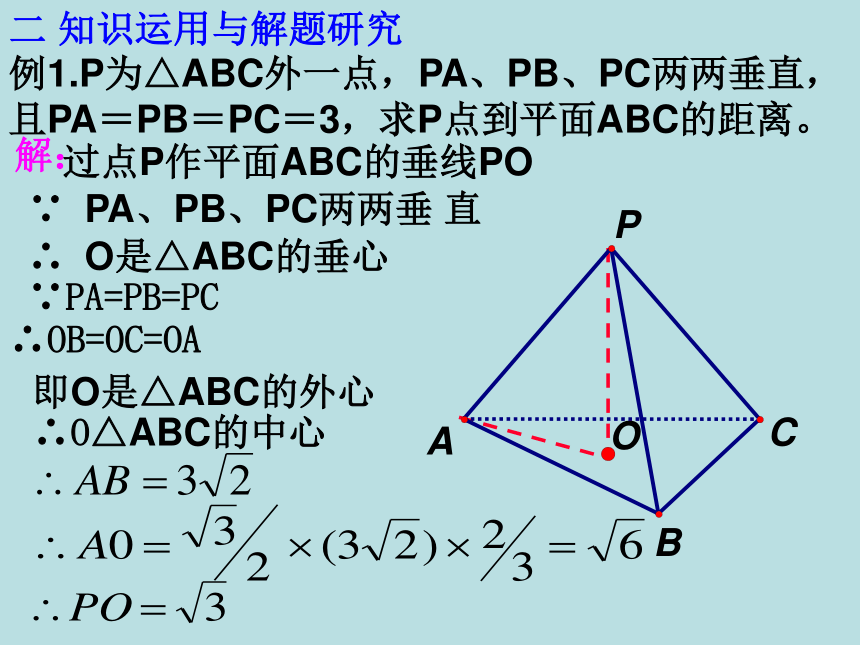
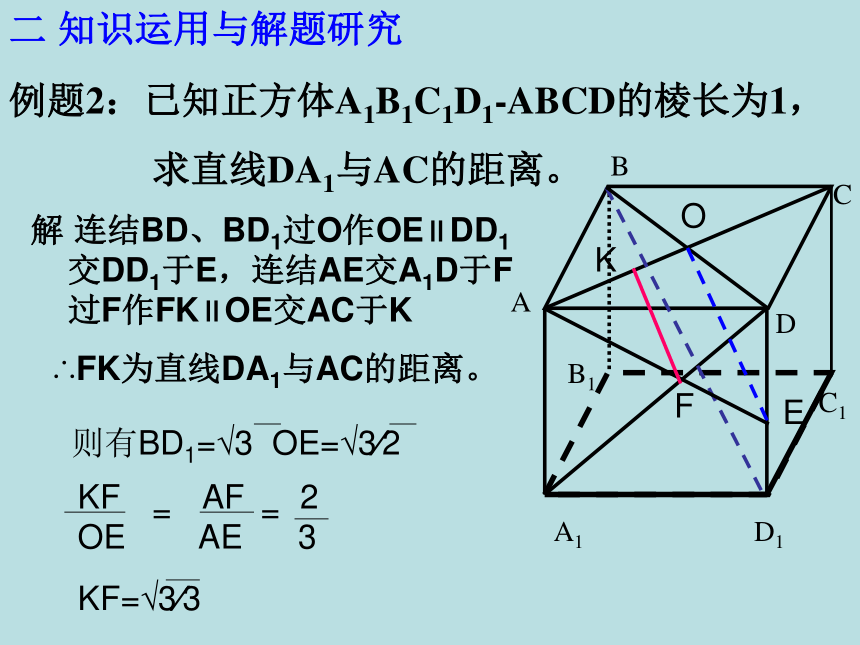
叫做两条异面直线的距离一 复习回顾各种距离的求法:※1 直接法 线线距离→面面距离→ 线面距离 →点面距离→点线距离4 公式法5 向量法2 转化法3 等积法一 复习回顾6 构造函数法 两条异面直线间的距离公式﹚aa′bAA1EFθ或π-θmndl︱EF︱2=︱EA+AA1+A1F︱2l2=m2+d2+n2 +2cosθ=︱EA︱2+︱AA1︱2+︱AF︱2+2EA·A1Fd=√l2-m2-n2 + 2mncosθd=√l2-m2-n2 + 2mncosθl=√m2+d2+n2 +2cosθcosθ=d2+m2+n2-l22mn∣ ∣1学习目标1 熟练掌握各种距离定义2 熟练掌握各种距离的求法3 能灵活运用上述知识方法解决相关问题,提高空间想象能力和逻辑推理能力例1.P为△ABC外一点,PA、PB、PC两两垂直,且PA=PB=PC=3,求P点到平面ABC的距离。ABCP过点P作平面ABC的垂线PO∵ PA、PB、PC两两垂 直解:∴ O是△ABC的垂心即O是△ABC的外心∵PA=PB=PC∴OB=OC=OA∴O△ABC的中心二 知识运用与解题研究D1C1B1A1DCBA例题2:已知正方体A1B1C1D1-ABCD的棱长为1,
求直线DA1与AC的距离。
OEFK二 知识运用与解题研究解 连结BD、BD1过O作OE∥DD1
交DD1于E,连结AE交A1D于F
过F作FK∥OE交AC于K则有BD1=√3 OE=√3∕2KF AF 2
OE AE 3==KF=√3∕3∴FK为直线DA1与AC的距离。
ED1C1B1A1DCBA※例题2:已知正方体A1B1C1D1-ABCD的棱长为1
求直线 DA1与AC的距离。OO1解:连结DO1,OO1,作OE垂直DO1交DO1于E则B1D1⊥A1C1 A1C1⊥OO1∴A1C1⊥平面BB1D1D∴平面DA1C1⊥平面BB1D1D∴OE⊥平面DA1C1∴OE⊥DO1∵OO1⊥OD OO1=1 OD=√2/2
DO1=√6/2∴OE=√3/3∵AC∥平面DA1C1∴直线DA1与AC的距离是√3/3D1B1A1DCBAC1O∵ D1A1、D1D、D1C1两两垂直解:∴ O是△A1DC1的垂心∵D1A1=D1D=D1C1∴OD1=OC1=OA1∴O△A1DC1的中心即O是△ABC的外心∕3∕3D1C1B1A1DCBAOVA1-AB1C=VC-AA1B1D1C1B1A1DCBAEMN设AE=x ME=x EN=√2∕2 ·(1-x)
NM=y
y2=x2+[√2∕2(1-x)2]2
3
2(x- )2+1
31
3=D1C1B1A1DCBAMNXYZ AA1·D1B
︱AA1︱·︱D1B︱d=PABCDEF三 练习反馈2已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,点E
为CC1中点,点F为BD1中点.
(1)求证:EF为BD1与CC1的公垂线
(2)求点D1到平面BDE的距离ABCDA1B1C1D1EFM2√3
3各种距离的求法:※1 直接法 线线距离→面面距离→ 线面距离 →点面距离→点线距离4 公式法5 向量法2 转化法3 等积法课堂总结6 构造函数法
一点到它在一个平面内的正射影的距离
叫做这一点到这个平面的距离
2 直线到与它平行平面的距离
一条直线上的任意点到与它平行的平面的距离
叫做这条直线到平面的距离
3 两个平行平面的距离
两个平行平面的公垂线段的长度
叫做两个平行平面的距离
4 异面直线的距离
两条异面直线的公垂线段的长度
叫做两条异面直线的距离一 复习回顾各种距离的求法:※1 直接法 线线距离→面面距离→ 线面距离 →点面距离→点线距离4 公式法5 向量法2 转化法3 等积法一 复习回顾6 构造函数法 两条异面直线间的距离公式﹚aa′bAA1EFθ或π-θmndl︱EF︱2=︱EA+AA1+A1F︱2l2=m2+d2+n2 +2cosθ=︱EA︱2+︱AA1︱2+︱AF︱2+2EA·A1Fd=√l2-m2-n2 + 2mncosθd=√l2-m2-n2 + 2mncosθl=√m2+d2+n2 +2cosθcosθ=d2+m2+n2-l22mn∣ ∣1学习目标1 熟练掌握各种距离定义2 熟练掌握各种距离的求法3 能灵活运用上述知识方法解决相关问题,提高空间想象能力和逻辑推理能力例1.P为△ABC外一点,PA、PB、PC两两垂直,且PA=PB=PC=3,求P点到平面ABC的距离。ABCP过点P作平面ABC的垂线PO∵ PA、PB、PC两两垂 直解:∴ O是△ABC的垂心即O是△ABC的外心∵PA=PB=PC∴OB=OC=OA∴O△ABC的中心二 知识运用与解题研究D1C1B1A1DCBA例题2:已知正方体A1B1C1D1-ABCD的棱长为1,
求直线DA1与AC的距离。
OEFK二 知识运用与解题研究解 连结BD、BD1过O作OE∥DD1
交DD1于E,连结AE交A1D于F
过F作FK∥OE交AC于K则有BD1=√3 OE=√3∕2KF AF 2
OE AE 3==KF=√3∕3∴FK为直线DA1与AC的距离。
ED1C1B1A1DCBA※例题2:已知正方体A1B1C1D1-ABCD的棱长为1
求直线 DA1与AC的距离。OO1解:连结DO1,OO1,作OE垂直DO1交DO1于E则B1D1⊥A1C1 A1C1⊥OO1∴A1C1⊥平面BB1D1D∴平面DA1C1⊥平面BB1D1D∴OE⊥平面DA1C1∴OE⊥DO1∵OO1⊥OD OO1=1 OD=√2/2
DO1=√6/2∴OE=√3/3∵AC∥平面DA1C1∴直线DA1与AC的距离是√3/3D1B1A1DCBAC1O∵ D1A1、D1D、D1C1两两垂直解:∴ O是△A1DC1的垂心∵D1A1=D1D=D1C1∴OD1=OC1=OA1∴O△A1DC1的中心即O是△ABC的外心∕3∕3D1C1B1A1DCBAOVA1-AB1C=VC-AA1B1D1C1B1A1DCBAEMN设AE=x ME=x EN=√2∕2 ·(1-x)
NM=y
y2=x2+[√2∕2(1-x)2]2
3
2(x- )2+1
31
3=D1C1B1A1DCBAMNXYZ AA1·D1B
︱AA1︱·︱D1B︱d=PABCDEF三 练习反馈2已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,点E
为CC1中点,点F为BD1中点.
(1)求证:EF为BD1与CC1的公垂线
(2)求点D1到平面BDE的距离ABCDA1B1C1D1EFM2√3
3各种距离的求法:※1 直接法 线线距离→面面距离→ 线面距离 →点面距离→点线距离4 公式法5 向量法2 转化法3 等积法课堂总结6 构造函数法
