2025年秋人教版七年级数学上册 6.2 直线、射线、线段 课件(共82张PPT)
文档属性
| 名称 | 2025年秋人教版七年级数学上册 6.2 直线、射线、线段 课件(共82张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 11:34:29 | ||
图片预览







文档简介
(共82张PPT)
6.2 直线、射线、线段
6.2.1 直线、射线、线段
第六章 几何图形初步
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
直线
射线
线段
基本事实 经过两点有一条直线,并且只有一条直线,简述为两点确定一条直线
表示方法 (1)用直线上任意表示两个点的大写字母表示,如直线AB;(2)用
一个小写字母表示,如直线l
特征 (1)无端点;(2)向两边无限延伸;(3)不可度量
知识点
直线
知1-讲
1
1. 认识直线
特别解读
“有”表 示 存在,“只有”表示唯一,即过两点一定能画出一条直线,且这样的直线唯一.
知1-讲
2. 点与直线的位置关系
图示 位置关系
(1)点在直线上(直线经过该点),如左图点A 在直线l 上(直线l 经过点A);
(2)点在直线外(直线不经过该点),如左图点B 在直线l 外(直线l 不经过点B)
知1-讲
3. 相交直线
(1)两条直线相交:当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫作它们的交点. 如图6 .2 -1①,可以说成直线a 与直线b 相交于点O.
知1-讲
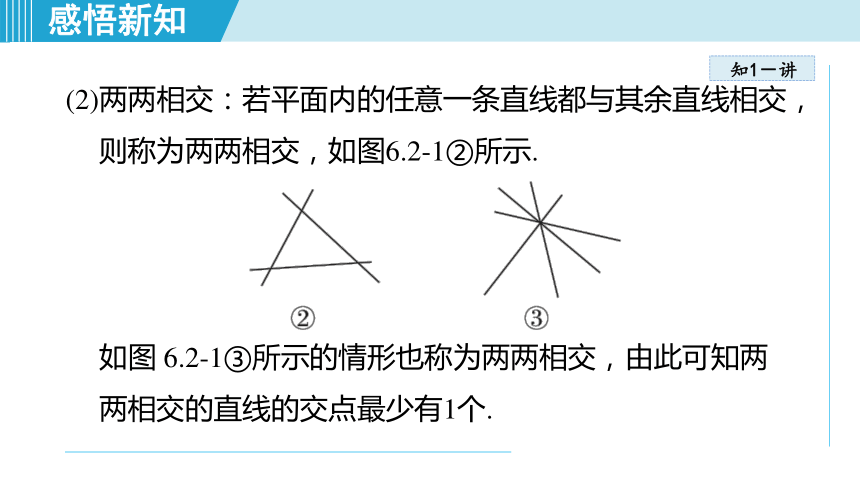
(2)两两相交:若平面内的任意一条直线都与其余直线相交,则称为两两相交,如图6.2-1②所示.
如图 6.2-1③所示的情形也称为两两相交,由此可知两两相交的直线的交点最少有1个.
知1-讲
特别提醒
1.用两个大写字母表示直线时,字母无顺序;
2.两条直线相交时,有且只有一个交点,如果交点个数不唯一,那么这两条直线重合;
3.直线上有无数个点,经过一点的直线有无数条.
知1-练
例 1
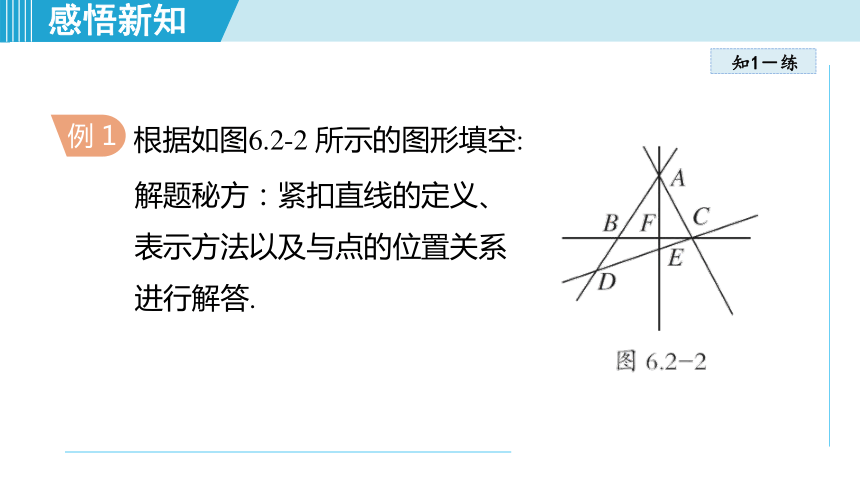
根据如图6.2-2 所示的图形填空:
解题秘方:紧扣直线的定义、表示方法以及与点的位置关系进行解答.
知1-练
(1)点B 在直线AD_______,点C 在直线AD _______ ;
(2)点E 是直线_________________与直线______________的交点,直线BC与直线AE 相交于点_______ ;
(3)过点A 的直线有_______条,它们分别是_____________
___________________________________ .
上
外
AF(或AE 或EF)
CD(或DE或CE)
F
3
直线AD(或AB
或BD),直线AC,直线AE(或AF 或EF)
知1-练
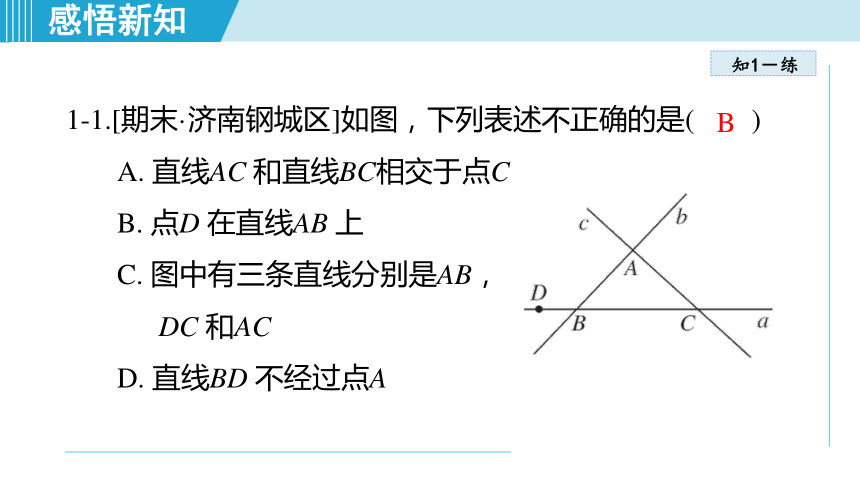
1-1.[期末·济南钢城区]如图,下列表述不正确的是( )
A. 直线AC 和直线BC相交于点C
B. 点D 在直线AB 上
C. 图中有三条直线分别是AB,
DC 和AC
D. 直线BD 不经过点A
B
知1-练
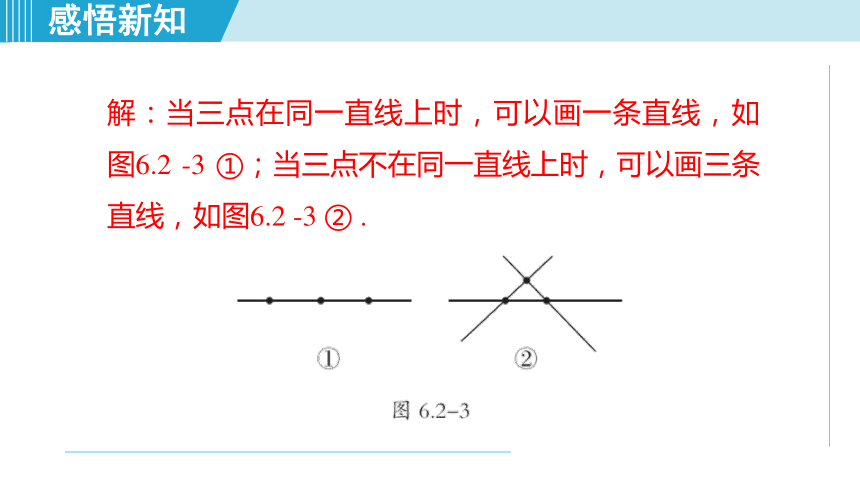
平面内有三个点,过其中任意两点画直线,一共可以画几条直线?画图加以说明.
例 2
解题秘方:紧扣“直线的基本事实”,根据三点的位置情况,逐一画出图形.
解:当三点在同一直线上时,可以画一条直线,如图6.2 -3 ①;当三点不在同一直线上时,可以画三条直线,如图6.2 -3 ② .
知1-练
2-1. 如图,3 条直线两两相交最多有3 个交点,4 条直线两两相交最多有6 个交点,按照这样的规律,则20 条直线两两相交最多有________个交点.
190
知2-讲
知识点
射线
2
1. 认识射线
定义 直线上一点和它一旁的部分叫作射线,这一点叫作射线的端点
表示 (1)用射线的端点和射线上另外一点的两个大写字母表示(表示端点的字母必须写在前面),如: 射线OA;(2)用一个小写字母表示,如: 射线l
特征 有一个端点,不可度量,可以向一个方向无限延伸
知2-讲
2. 射线的识别
端点情况 描述 图示
端点相同 端点相同,延伸方向也相同的射线是同一条射线,如射线OA,射线OB 表示同一条射线
端点相同,但延伸方向不同的射线不是同一条射线,如射线AO 与射线AB 不是同一条射线 端点不同 端点不同的射线一定不是同一条射线,如射线OA,射线AB 不是同一条射线
知2-讲
特别提醒
1.不论用大写字母还是小写字母表示射线,都必须标明“射线××”.
2.由于射线可以向一个方向无限延伸,因此射线没有延长线,但它有反向延长线,如图6.2-4是反向延长射线OA 到点P.
3.若一条直线上有n个点,则在这条直线上可以找到2n条射线.
知2-练
如图 6.2-5 所示,图中有几条射线?其中可以用两个大写字母表示的是哪几条?
例 3
解题秘方:在确定射线时要抓住两点:(1)确定端点;(2)确定延伸方向,同时还要结合题目要求正确理解“图中有几条射线”与“图中能用两个大写字母表示的射线是哪几条”.
知2-练
解:图中有8条射线,其中可以用两个大写字母表示的有6条,分别是射线AB(AC或AD)、射线BA(BD或BC)、射线CA、射线 CB(CD)、射线 DA(DC)、射线 DB.
知2-练
规律总结:若一条直线上有n个点,则有2n条射线.若用n个大写字母表示这n个点,则可用两个大写字母表示的射线有 2(n-1)条.
知2-练
3-1.[期末·南阳卧龙区]如图, 点C 为直线AB外一点,作射线AC,连接BC,则图中共含有______条射线.
6
知3-讲
知识点
线段
3
1. 认识线段
定义 直线上两点及两点间的部分叫作线段,这两个点叫作线段的端点
表示 方法 (1)用线段的两个端点的大写字母表示,如线段AB;(2)用一个小写字母表示,
如线段a
特征 (1)两个端点;(2)无方向;(3)有长短
知3-讲
2. 直线、射线、线段的区别与联系
直线 射线 线段
区别 图形
表示方法 直线AB 或直线BA 或直线l 射线OA 或射线l 线段AB 或线段BA 或线段a
端点个数 0 1 2
延伸情况 向两方无限延伸 向一方无限延伸 不能延伸
度量情况 不能度量 不能度量 能度量
联系 射线和线段都是直线的一部分;线段向一方无限延伸就成为射线,向两方无限延伸就成为直线;射线向反方向无限延伸就成为直线
知3-讲
3. 与线段有关的作图语言举例
(1)连接AB:画以A,B 为端点的线段;
(2)延长线段AB:是指从端点A 到B 的方向延长;
(3)反向延长线段AB:是指从端点A 到B 相反的方向延长,即延长线段BA.
知3-讲
特别解读
1. 线段、射线、直线表示方法都一样,只是射线有方向性,故用两个大写字母表示时有顺序,而线段和直线没有方向性.
2. 在用两个大写字母表示直线、射线、线段时,两个大写字母前面还应加上直线、射线、线段,其中表示线段时,“线段”两个字可以省略.
知3-讲
特别提醒
延长是有方向的:是指从前面端点向后面端点的方向,所以说延长线段AB 与延长线段BA是不一样的,它们的方向相反.
知3-练
如图6.2-6,表示方法正确的是( )
A. ① ② B. ② ④ C. ③ ④ D. ①④
例 4
知3-练
解题秘方:根据直线、射线、线段的表示方法逐一判断.
解:
序号 理由 结论
① 不能用一个大写字母表示直线 ×
② 可以用一个小写字母表示射线 √
③ 应表示为射线 OA ×
④ 可以用表示线段两个端点的大写字母表示线段 √
答案:B
知3-练
4-1. 如图所示, 下列对图形描述不正确的是( )
A. 直线AB
B. 线段BC
C. 射线CA
D. 射线AB
C
知3-练
如图6.2-7,在平面内有四个点A,B,C,D,请你用直尺按下列要求画图:
(1)画射线CD;
(2)画直线AD;
(3)连接AB;
(4)画线段BD 与直线AC 相交于点O.
例 5
知3-练
思路导引:
解:(1)(2)(3)(4)如图6 .2-7 所示.
知3-练
5-1. 如图,在平面内有A,B,C 三点.
(1)画直线AC、线段BC、射线AB;
(2)在线段BC 上任取一点D(不同于B,C),画线段AD;
(3)数数看,此时图中线段的条数.
解:(1)(2)如图所示.
此时图中线段的条数为6.
直线、射线、线段
(三线)直线、射线、线段
定义
表示法
端点数
直线的确定性
6.2 直线、射线、线段
6.2.2 线段的比较与运算
第六章 几何图形初步
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
线段的画法及长短比较
线段的基本事实及两点间的距离
线段和、差的意义及作法
线段的中点及倍、分
知识点
线段的画法及长短比较
知1-讲
1
1. 尺规作图 在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
知1-讲
2. 画一条线段等于已知线段a
(1)方法一(测量作图):利用刻度尺先量出已知线段a 的长度,再画一条等于这个长度的线段.
(2)方法二(尺规作图):如图6.2 -12,用直尺画射线AC,再用圆规在射线AC 上截取AB=a
(这就是“作一条线段等于已知
线段”的尺规作图).
知1-讲
3.线段长短的比较方法
(1)观察法:通过直观的视觉观察,判断两条线段的长短.两条线段的长短相差很明显时,一般采用这种方法.
(2)叠合法(形的比较):把要比较的两条线段的一个端点重合,然后将两条线段在重合点的同侧叠合在一起,由另一个端点的位置关系可以得出两条线段的长短关系.
知1-讲
叠合法比较线段长短 图例 结论
ABAB=CD
AB>CD
知1-讲
(3)度量法(数的比较):用刻度尺测量出线段的长度(单位相同),再根据长度的大小判断线段的长短关系
如图 6.2-13 所示,已知线段AB,CD,通过测量得AB=1.5 cm,CD=2 cm,可判定AB知1-讲
特别解读
1.比较线段的长短实质就是比较线段长度的大小.
2.当两条线段的长短差别不大,且又不便放在一起比较时,运用度量法;当两条线段能够放在一起且又不需要知道相差的具体数值时,可用叠合法.
3.度量法和叠合法是从“数”和“形”两个方面进行的,从“数”的方面比较,一般用度量法;从“形”的方面比较,一般用叠合法.
4.叠合法简记为“共端点,同方向,叠一起,比长短”
知1-练
例 1
如图6.2-14 是一张三角形纸片,你能比较线段AB 与线段BC 的长短吗?
解题秘方:可以利用度量法,分别量出两条线段的长度,然后进行比较,或者利用叠合法进行比较.
解:方法一 度量法.
用刻度尺量得AB=1.7cm,BC=1.3cm,所以AB>BC.
方法二 叠合法.
如图6.2-14 ,将圆规的针尖放在B点,
笔尖放在C 点,将圆规绕B 点旋转,
圆弧与AB 交于D 点.所以AB>BC.
知1-练
1-1. 要比较线段AB与CD 的长短, 小明将点A 与点C 重合并使两条线段在一条直线上, 结果点B 在CD 的延长线上, 则AB与CD相比较,( )
A.ABB.AB>CD
C.AB=CD
D. 无法判断
B
知2-讲
知识点
线段的基本事实
2
线段的基本事实 两点的距离 举例
两点的所有连线中,线段最短. 简单说成:两点之间,线段最短 定义 性质
在所有连接A,B 两点的线中,线段AB是最短的,线段AB 的长度就是点A 与点B 之间的距离
连接两点的线段的长度,叫作这两点间的距离 (1)存在性; (2)最短性; (3)唯一性
知2-讲
警示误区
两点的距离是一个具体的数量,而线段本身是图形.因此不能把A,B 两点的距离说成是线段AB. 另外,连接两点是指画出以这两点为端点的线段.
知2-练
下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB 架设;
④把弯曲的公路改直,就能缩短路程。
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
例 2
解题秘方:根据直线、线段的基本事实判断,注意两个基本事实的区别.
解:①②现象可以用“两点确定一条直线”来解释;③④现象可以用“两点之间,线段最短”来解释.
答案:D
知2-练
2-1.下列四种实践方式:①木匠弹墨线;②打靶瞄准;③过马路时,人们总喜欢走直的,不喜欢走折的路线;④拉绳插秧.其中可以用基本事实“两点确定一条直线”来解释的有(填序号)__________.
①②④
知2-练
例 3
[母题教材P188复习题T14]如图6.2-15,已知A,B,C,D为四个居民小区,现要建一个购物中心,不考虑其他因素,请你画图确定购物中心O的位置,使它到四个居民小区的距离之和最小.
两点之间,线段最短
知2-练
思路引导:
知2-练
解:如图6.2-16,连接AC,BD相交于点O,点O就是购物中心的位置,这一点到四个居民小区的距离之和最小.
知2-练
3-1.小明打算从汽车站 A 去火车站 F,他不知道怎么走最近,于是参照手机地图,地图给出了如图所示的四条路线,你认为小明应该走哪条路线(用字母表示)?为什么?
知2-练
解:小明应该按照AB→BE→EF的方式走,因为两点之间,线段最短.
知2-练
如图6.2-17,有一个正方体盒子放在桌面上,一只虫子在顶点A 处,一只蜘蛛在顶点B 处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,应该怎样走?你能画出来吗?
例 4
知2-练
解题秘方:蜘蛛要想最快地捉住虫子,需走最短的路径,而蜘蛛走的路径是正方体的不同侧面,因此应在正方体的侧面展开图中寻找.
其实质是把立体图形展开为平面图形,也就是把正方体的不同侧面展开到同一平面,利用“两点之间,线段最短”确定最短的路径.
知2-练
解:如图6.2-1-8 ,有四种走法,分别是:B → F → A,B → G → A,B → M → A,B → N → A(F,G,M,N 分别为DE,CD,KE,KH 的中点).
知2-练
方法点拨:在现实生活中,从A 地到B 地,若要路程最短,则A,B 之间画成笔直的线,若要路程变长,则画成折线或曲线,各有用途,根据不同需求进行设计.
知2-练
4-1. 如图,一观测塔底座部分是长方体,现在从下底面A点修建扶梯,经过点M,N到点D′,再进入顶部的观测室,已知AB=BC,试确定使扶梯的总长度最小的点M,N 的位置.
解:如图,将长方体的三个面展开,连接AD′,分别与BB′,CC′交于点M,N,点M,N即为所求.
知3-讲
知识点
线段和、差的意义及作法
3
如图6.2-19 ,已知线段a,b(且a>b).
知3-讲
(1)线段的和:在直线l 上作线段AB=a,再在AB 的
延长线上作线段BC=b,线段AC 就是a 与b 的和,记作AC=a+b,如图6.2-20① .
(2)线段的差:在直线l 上作线段AB=a,再在线段AB 上作线段BD=b,则线段AD 就是a 与b 的差,记作AD=a-b,如图6.2-20 ② .
知3-讲
特别提醒
线段和、差的作图方法
知3-练
[母题教材P166练习T2]用直尺和圆规作线段:如图6.2-21,已知线段a,b,c.
(1)求作一条线段,使它等于a+2b;
(2)求作一条线段,使它等于a-b+c.
解题秘方:按照线段和差的作法用圆规在射线上依次截取.
例 5
知3-练
解:(1)如图6.2-22,
1.作射线AM;
2.在射线AM上顺次截取AB=a,BC=CD=b.
线段 AD 即为所求作.
知3-练
(2)如图 6.2-23,
1.作射线AM;
2.在射线AM上顺次截取AB=a,BC=c;
3.在线段AC上截取CD=b.
线段 AD 即为所求作.
知3-练
5-1.已 知:线 段 a,b.求作:线段 AB,使得
AB=2a+b.小明给出了四个步骤(如图):
①作一条射线 AE;②则线段 AB=2a+b;
③在射线 AE 上作线段AC=a,再在射线 CE 上作线段CD=a;④在射线 DE 上作线段DB=b.
你认为顺序正确的是( )
A.②①③④ B.①③④②
C.①④③② D.④①③②
B
知4-讲
知识点
线段和、差的意义及作法
3
1. 线段的中点
把一条线段分成两条相等线段的点,叫作线段的中点. 如图6.2-24 ,如果M 是线段AB 的中点,则有AM=BM=AB.
2. 等分点
(1)把一条线段分成三条相等的线段的点叫作线段的三等分点. 如图6.2-25,M,N 是线段AB 的三等分点,则有AM=MN=NB=AB.
(2)把一条线段分成四条相等的线段的点叫作线段的四等分点. 如图6.2-26 ,M,N,P 是线段AB 的四等分点,则有AM=MN=NP=PB=AB.
知4-讲
知4-讲
3. 线段的倍、分的意义:“线段的倍”指的是一条线段的长度是另一条线段长度的几倍;“线段的分”指的是一条线段的长度是另一条线段长度的几分之几.
如图6.2-27所示,射线AE上有B,C,D三点,它们的长度关系是AB=BC=CD,则AC=2BC,AD=3AB,AB=AC,AB=AD,AC=AD.
知4-讲
特别提醒
1.线段的中点必须在线段上,并且只有一个.
2.线段的中点可以转化为线段相等或成倍分关系的等式,但是相等或倍分关系不一定能转化为线段的中点,如若AC=BC,如果点C不在线段AB上,就不是线段AB的中点.
3.线段的中点及等分点的特征: 这些点都在线段上,线段的中点只有一个,线段的三等分点、四等分点不止一个.
知4-练
下列说法中,能说明点P是线段AB中点的是_______.
①AP=AB;②AP=PB;③AB=2PB;④AP=PB=AB.
例 6
解:
选项 图例 点P是否为线段AB的中点
① 否
② 否
③ 否
④ 是
④
知4-练
易错警示:线段的中点一定要在线段上,并且满足到两个端点的距离相等,在实际证明过程中易忽略“点在线段上”的条件限制,从而导致判断错误.
知4-练
6-1.[期末·台州玉环市]在一条直线上从左到右依次有 A,B,C 三点,以下语句不能判定点B 是线段 AC 中点的是( )
A.AB+BC=AC B.AB=BC
C.AC=2BC D.AB=AC
A
知4-练
如图 6.2-28,点 B,C,D在线段AE上,BC=CD.
(1)BD=______CD,BC=______BD.
(2)若DE=CD,则AD-2DE=______,AB+2BC=______,AΕ-BE=______.
例 7
2
AB
AD
AC
知4-练
解:(1)因为 BC=CD,所以BD=2CD,BC=BD.
(2)因为BC=CD,DE=CD,所以BC=CD=DE.
所以AD-2DE=AD-(BC+CD)=AD-BD=AB,AB+BC=AB+BC+CD=AD,
AE-BE=AE-DE=AE-2DE=AE-(CD+DE)=AE-CE=AC.
知4-练
7-1.如图所示,若 BC=CD,则 BD=______CD,BC=______BD,BC______CE,AC______CD(后两空填“>”“<”或“=”).
2
<
>
知4-练
如图 6.2-29 所示,AC=8 cm,CB=6 cm,如果 O 是线段AB的中点,求线段OC的长度.
例 8
知4-练
思路引导:
知4-练
解:因为AB=AC+CB=8+6-14(cm),
O是线段AB的中点,所以AO=OB===7(cm),
所以OC=OB-CB=7-6=1(cm).
另解
OC=AC-AO=8-7=1(cm).
知4-练
素养点拨:本题以线段的中点为主要考点进行了线段的和差计算,进一步体会线段的和差与线段长度和差的关系,领悟数的运算策略和方法在数量运算中的运用,培养了运算能力.
知4-练
8-1.[新考法 分类讨论法]已知线 段 AC 和线 段BC 在同一直线上,如果AC=6 cm,BC=4 cm,则线段 AC 的中点和线段 BC 的中点之间的距离为______cm.
1或5
线段的比较与运算
线段的比较与运算
线段的比较
线段的运算
度量法
叠合法
线段的和差
线段的中点
6.2 直线、射线、线段
6.2.1 直线、射线、线段
第六章 几何图形初步
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
直线
射线
线段
基本事实 经过两点有一条直线,并且只有一条直线,简述为两点确定一条直线
表示方法 (1)用直线上任意表示两个点的大写字母表示,如直线AB;(2)用
一个小写字母表示,如直线l
特征 (1)无端点;(2)向两边无限延伸;(3)不可度量
知识点
直线
知1-讲
1
1. 认识直线
特别解读
“有”表 示 存在,“只有”表示唯一,即过两点一定能画出一条直线,且这样的直线唯一.
知1-讲
2. 点与直线的位置关系
图示 位置关系
(1)点在直线上(直线经过该点),如左图点A 在直线l 上(直线l 经过点A);
(2)点在直线外(直线不经过该点),如左图点B 在直线l 外(直线l 不经过点B)
知1-讲
3. 相交直线
(1)两条直线相交:当两条不同的直线有一个公共点时,就称这两条直线相交,这个公共点叫作它们的交点. 如图6 .2 -1①,可以说成直线a 与直线b 相交于点O.
知1-讲
(2)两两相交:若平面内的任意一条直线都与其余直线相交,则称为两两相交,如图6.2-1②所示.
如图 6.2-1③所示的情形也称为两两相交,由此可知两两相交的直线的交点最少有1个.
知1-讲
特别提醒
1.用两个大写字母表示直线时,字母无顺序;
2.两条直线相交时,有且只有一个交点,如果交点个数不唯一,那么这两条直线重合;
3.直线上有无数个点,经过一点的直线有无数条.
知1-练
例 1
根据如图6.2-2 所示的图形填空:
解题秘方:紧扣直线的定义、表示方法以及与点的位置关系进行解答.
知1-练
(1)点B 在直线AD_______,点C 在直线AD _______ ;
(2)点E 是直线_________________与直线______________的交点,直线BC与直线AE 相交于点_______ ;
(3)过点A 的直线有_______条,它们分别是_____________
___________________________________ .
上
外
AF(或AE 或EF)
CD(或DE或CE)
F
3
直线AD(或AB
或BD),直线AC,直线AE(或AF 或EF)
知1-练
1-1.[期末·济南钢城区]如图,下列表述不正确的是( )
A. 直线AC 和直线BC相交于点C
B. 点D 在直线AB 上
C. 图中有三条直线分别是AB,
DC 和AC
D. 直线BD 不经过点A
B
知1-练
平面内有三个点,过其中任意两点画直线,一共可以画几条直线?画图加以说明.
例 2
解题秘方:紧扣“直线的基本事实”,根据三点的位置情况,逐一画出图形.
解:当三点在同一直线上时,可以画一条直线,如图6.2 -3 ①;当三点不在同一直线上时,可以画三条直线,如图6.2 -3 ② .
知1-练
2-1. 如图,3 条直线两两相交最多有3 个交点,4 条直线两两相交最多有6 个交点,按照这样的规律,则20 条直线两两相交最多有________个交点.
190
知2-讲
知识点
射线
2
1. 认识射线
定义 直线上一点和它一旁的部分叫作射线,这一点叫作射线的端点
表示 (1)用射线的端点和射线上另外一点的两个大写字母表示(表示端点的字母必须写在前面),如: 射线OA;(2)用一个小写字母表示,如: 射线l
特征 有一个端点,不可度量,可以向一个方向无限延伸
知2-讲
2. 射线的识别
端点情况 描述 图示
端点相同 端点相同,延伸方向也相同的射线是同一条射线,如射线OA,射线OB 表示同一条射线
端点相同,但延伸方向不同的射线不是同一条射线,如射线AO 与射线AB 不是同一条射线 端点不同 端点不同的射线一定不是同一条射线,如射线OA,射线AB 不是同一条射线
知2-讲
特别提醒
1.不论用大写字母还是小写字母表示射线,都必须标明“射线××”.
2.由于射线可以向一个方向无限延伸,因此射线没有延长线,但它有反向延长线,如图6.2-4是反向延长射线OA 到点P.
3.若一条直线上有n个点,则在这条直线上可以找到2n条射线.
知2-练
如图 6.2-5 所示,图中有几条射线?其中可以用两个大写字母表示的是哪几条?
例 3
解题秘方:在确定射线时要抓住两点:(1)确定端点;(2)确定延伸方向,同时还要结合题目要求正确理解“图中有几条射线”与“图中能用两个大写字母表示的射线是哪几条”.
知2-练
解:图中有8条射线,其中可以用两个大写字母表示的有6条,分别是射线AB(AC或AD)、射线BA(BD或BC)、射线CA、射线 CB(CD)、射线 DA(DC)、射线 DB.
知2-练
规律总结:若一条直线上有n个点,则有2n条射线.若用n个大写字母表示这n个点,则可用两个大写字母表示的射线有 2(n-1)条.
知2-练
3-1.[期末·南阳卧龙区]如图, 点C 为直线AB外一点,作射线AC,连接BC,则图中共含有______条射线.
6
知3-讲
知识点
线段
3
1. 认识线段
定义 直线上两点及两点间的部分叫作线段,这两个点叫作线段的端点
表示 方法 (1)用线段的两个端点的大写字母表示,如线段AB;(2)用一个小写字母表示,
如线段a
特征 (1)两个端点;(2)无方向;(3)有长短
知3-讲
2. 直线、射线、线段的区别与联系
直线 射线 线段
区别 图形
表示方法 直线AB 或直线BA 或直线l 射线OA 或射线l 线段AB 或线段BA 或线段a
端点个数 0 1 2
延伸情况 向两方无限延伸 向一方无限延伸 不能延伸
度量情况 不能度量 不能度量 能度量
联系 射线和线段都是直线的一部分;线段向一方无限延伸就成为射线,向两方无限延伸就成为直线;射线向反方向无限延伸就成为直线
知3-讲
3. 与线段有关的作图语言举例
(1)连接AB:画以A,B 为端点的线段;
(2)延长线段AB:是指从端点A 到B 的方向延长;
(3)反向延长线段AB:是指从端点A 到B 相反的方向延长,即延长线段BA.
知3-讲
特别解读
1. 线段、射线、直线表示方法都一样,只是射线有方向性,故用两个大写字母表示时有顺序,而线段和直线没有方向性.
2. 在用两个大写字母表示直线、射线、线段时,两个大写字母前面还应加上直线、射线、线段,其中表示线段时,“线段”两个字可以省略.
知3-讲
特别提醒
延长是有方向的:是指从前面端点向后面端点的方向,所以说延长线段AB 与延长线段BA是不一样的,它们的方向相反.
知3-练
如图6.2-6,表示方法正确的是( )
A. ① ② B. ② ④ C. ③ ④ D. ①④
例 4
知3-练
解题秘方:根据直线、射线、线段的表示方法逐一判断.
解:
序号 理由 结论
① 不能用一个大写字母表示直线 ×
② 可以用一个小写字母表示射线 √
③ 应表示为射线 OA ×
④ 可以用表示线段两个端点的大写字母表示线段 √
答案:B
知3-练
4-1. 如图所示, 下列对图形描述不正确的是( )
A. 直线AB
B. 线段BC
C. 射线CA
D. 射线AB
C
知3-练
如图6.2-7,在平面内有四个点A,B,C,D,请你用直尺按下列要求画图:
(1)画射线CD;
(2)画直线AD;
(3)连接AB;
(4)画线段BD 与直线AC 相交于点O.
例 5
知3-练
思路导引:
解:(1)(2)(3)(4)如图6 .2-7 所示.
知3-练
5-1. 如图,在平面内有A,B,C 三点.
(1)画直线AC、线段BC、射线AB;
(2)在线段BC 上任取一点D(不同于B,C),画线段AD;
(3)数数看,此时图中线段的条数.
解:(1)(2)如图所示.
此时图中线段的条数为6.
直线、射线、线段
(三线)直线、射线、线段
定义
表示法
端点数
直线的确定性
6.2 直线、射线、线段
6.2.2 线段的比较与运算
第六章 几何图形初步
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
线段的画法及长短比较
线段的基本事实及两点间的距离
线段和、差的意义及作法
线段的中点及倍、分
知识点
线段的画法及长短比较
知1-讲
1
1. 尺规作图 在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
知1-讲
2. 画一条线段等于已知线段a
(1)方法一(测量作图):利用刻度尺先量出已知线段a 的长度,再画一条等于这个长度的线段.
(2)方法二(尺规作图):如图6.2 -12,用直尺画射线AC,再用圆规在射线AC 上截取AB=a
(这就是“作一条线段等于已知
线段”的尺规作图).
知1-讲
3.线段长短的比较方法
(1)观察法:通过直观的视觉观察,判断两条线段的长短.两条线段的长短相差很明显时,一般采用这种方法.
(2)叠合法(形的比较):把要比较的两条线段的一个端点重合,然后将两条线段在重合点的同侧叠合在一起,由另一个端点的位置关系可以得出两条线段的长短关系.
知1-讲
叠合法比较线段长短 图例 结论
AB
AB>CD
知1-讲
(3)度量法(数的比较):用刻度尺测量出线段的长度(单位相同),再根据长度的大小判断线段的长短关系
如图 6.2-13 所示,已知线段AB,CD,通过测量得AB=1.5 cm,CD=2 cm,可判定AB
特别解读
1.比较线段的长短实质就是比较线段长度的大小.
2.当两条线段的长短差别不大,且又不便放在一起比较时,运用度量法;当两条线段能够放在一起且又不需要知道相差的具体数值时,可用叠合法.
3.度量法和叠合法是从“数”和“形”两个方面进行的,从“数”的方面比较,一般用度量法;从“形”的方面比较,一般用叠合法.
4.叠合法简记为“共端点,同方向,叠一起,比长短”
知1-练
例 1
如图6.2-14 是一张三角形纸片,你能比较线段AB 与线段BC 的长短吗?
解题秘方:可以利用度量法,分别量出两条线段的长度,然后进行比较,或者利用叠合法进行比较.
解:方法一 度量法.
用刻度尺量得AB=1.7cm,BC=1.3cm,所以AB>BC.
方法二 叠合法.
如图6.2-14 ,将圆规的针尖放在B点,
笔尖放在C 点,将圆规绕B 点旋转,
圆弧与AB 交于D 点.所以AB>BC.
知1-练
1-1. 要比较线段AB与CD 的长短, 小明将点A 与点C 重合并使两条线段在一条直线上, 结果点B 在CD 的延长线上, 则AB与CD相比较,( )
A.AB
C.AB=CD
D. 无法判断
B
知2-讲
知识点
线段的基本事实
2
线段的基本事实 两点的距离 举例
两点的所有连线中,线段最短. 简单说成:两点之间,线段最短 定义 性质
在所有连接A,B 两点的线中,线段AB是最短的,线段AB 的长度就是点A 与点B 之间的距离
连接两点的线段的长度,叫作这两点间的距离 (1)存在性; (2)最短性; (3)唯一性
知2-讲
警示误区
两点的距离是一个具体的数量,而线段本身是图形.因此不能把A,B 两点的距离说成是线段AB. 另外,连接两点是指画出以这两点为端点的线段.
知2-练
下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB 架设;
④把弯曲的公路改直,就能缩短路程。
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A.①② B.①③ C.②④ D.③④
例 2
解题秘方:根据直线、线段的基本事实判断,注意两个基本事实的区别.
解:①②现象可以用“两点确定一条直线”来解释;③④现象可以用“两点之间,线段最短”来解释.
答案:D
知2-练
2-1.下列四种实践方式:①木匠弹墨线;②打靶瞄准;③过马路时,人们总喜欢走直的,不喜欢走折的路线;④拉绳插秧.其中可以用基本事实“两点确定一条直线”来解释的有(填序号)__________.
①②④
知2-练
例 3
[母题教材P188复习题T14]如图6.2-15,已知A,B,C,D为四个居民小区,现要建一个购物中心,不考虑其他因素,请你画图确定购物中心O的位置,使它到四个居民小区的距离之和最小.
两点之间,线段最短
知2-练
思路引导:
知2-练
解:如图6.2-16,连接AC,BD相交于点O,点O就是购物中心的位置,这一点到四个居民小区的距离之和最小.
知2-练
3-1.小明打算从汽车站 A 去火车站 F,他不知道怎么走最近,于是参照手机地图,地图给出了如图所示的四条路线,你认为小明应该走哪条路线(用字母表示)?为什么?
知2-练
解:小明应该按照AB→BE→EF的方式走,因为两点之间,线段最短.
知2-练
如图6.2-17,有一个正方体盒子放在桌面上,一只虫子在顶点A 处,一只蜘蛛在顶点B 处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,应该怎样走?你能画出来吗?
例 4
知2-练
解题秘方:蜘蛛要想最快地捉住虫子,需走最短的路径,而蜘蛛走的路径是正方体的不同侧面,因此应在正方体的侧面展开图中寻找.
其实质是把立体图形展开为平面图形,也就是把正方体的不同侧面展开到同一平面,利用“两点之间,线段最短”确定最短的路径.
知2-练
解:如图6.2-1-8 ,有四种走法,分别是:B → F → A,B → G → A,B → M → A,B → N → A(F,G,M,N 分别为DE,CD,KE,KH 的中点).
知2-练
方法点拨:在现实生活中,从A 地到B 地,若要路程最短,则A,B 之间画成笔直的线,若要路程变长,则画成折线或曲线,各有用途,根据不同需求进行设计.
知2-练
4-1. 如图,一观测塔底座部分是长方体,现在从下底面A点修建扶梯,经过点M,N到点D′,再进入顶部的观测室,已知AB=BC,试确定使扶梯的总长度最小的点M,N 的位置.
解:如图,将长方体的三个面展开,连接AD′,分别与BB′,CC′交于点M,N,点M,N即为所求.
知3-讲
知识点
线段和、差的意义及作法
3
如图6.2-19 ,已知线段a,b(且a>b).
知3-讲
(1)线段的和:在直线l 上作线段AB=a,再在AB 的
延长线上作线段BC=b,线段AC 就是a 与b 的和,记作AC=a+b,如图6.2-20① .
(2)线段的差:在直线l 上作线段AB=a,再在线段AB 上作线段BD=b,则线段AD 就是a 与b 的差,记作AD=a-b,如图6.2-20 ② .
知3-讲
特别提醒
线段和、差的作图方法
知3-练
[母题教材P166练习T2]用直尺和圆规作线段:如图6.2-21,已知线段a,b,c.
(1)求作一条线段,使它等于a+2b;
(2)求作一条线段,使它等于a-b+c.
解题秘方:按照线段和差的作法用圆规在射线上依次截取.
例 5
知3-练
解:(1)如图6.2-22,
1.作射线AM;
2.在射线AM上顺次截取AB=a,BC=CD=b.
线段 AD 即为所求作.
知3-练
(2)如图 6.2-23,
1.作射线AM;
2.在射线AM上顺次截取AB=a,BC=c;
3.在线段AC上截取CD=b.
线段 AD 即为所求作.
知3-练
5-1.已 知:线 段 a,b.求作:线段 AB,使得
AB=2a+b.小明给出了四个步骤(如图):
①作一条射线 AE;②则线段 AB=2a+b;
③在射线 AE 上作线段AC=a,再在射线 CE 上作线段CD=a;④在射线 DE 上作线段DB=b.
你认为顺序正确的是( )
A.②①③④ B.①③④②
C.①④③② D.④①③②
B
知4-讲
知识点
线段和、差的意义及作法
3
1. 线段的中点
把一条线段分成两条相等线段的点,叫作线段的中点. 如图6.2-24 ,如果M 是线段AB 的中点,则有AM=BM=AB.
2. 等分点
(1)把一条线段分成三条相等的线段的点叫作线段的三等分点. 如图6.2-25,M,N 是线段AB 的三等分点,则有AM=MN=NB=AB.
(2)把一条线段分成四条相等的线段的点叫作线段的四等分点. 如图6.2-26 ,M,N,P 是线段AB 的四等分点,则有AM=MN=NP=PB=AB.
知4-讲
知4-讲
3. 线段的倍、分的意义:“线段的倍”指的是一条线段的长度是另一条线段长度的几倍;“线段的分”指的是一条线段的长度是另一条线段长度的几分之几.
如图6.2-27所示,射线AE上有B,C,D三点,它们的长度关系是AB=BC=CD,则AC=2BC,AD=3AB,AB=AC,AB=AD,AC=AD.
知4-讲
特别提醒
1.线段的中点必须在线段上,并且只有一个.
2.线段的中点可以转化为线段相等或成倍分关系的等式,但是相等或倍分关系不一定能转化为线段的中点,如若AC=BC,如果点C不在线段AB上,就不是线段AB的中点.
3.线段的中点及等分点的特征: 这些点都在线段上,线段的中点只有一个,线段的三等分点、四等分点不止一个.
知4-练
下列说法中,能说明点P是线段AB中点的是_______.
①AP=AB;②AP=PB;③AB=2PB;④AP=PB=AB.
例 6
解:
选项 图例 点P是否为线段AB的中点
① 否
② 否
③ 否
④ 是
④
知4-练
易错警示:线段的中点一定要在线段上,并且满足到两个端点的距离相等,在实际证明过程中易忽略“点在线段上”的条件限制,从而导致判断错误.
知4-练
6-1.[期末·台州玉环市]在一条直线上从左到右依次有 A,B,C 三点,以下语句不能判定点B 是线段 AC 中点的是( )
A.AB+BC=AC B.AB=BC
C.AC=2BC D.AB=AC
A
知4-练
如图 6.2-28,点 B,C,D在线段AE上,BC=CD.
(1)BD=______CD,BC=______BD.
(2)若DE=CD,则AD-2DE=______,AB+2BC=______,AΕ-BE=______.
例 7
2
AB
AD
AC
知4-练
解:(1)因为 BC=CD,所以BD=2CD,BC=BD.
(2)因为BC=CD,DE=CD,所以BC=CD=DE.
所以AD-2DE=AD-(BC+CD)=AD-BD=AB,AB+BC=AB+BC+CD=AD,
AE-BE=AE-DE=AE-2DE=AE-(CD+DE)=AE-CE=AC.
知4-练
7-1.如图所示,若 BC=CD,则 BD=______CD,BC=______BD,BC______CE,AC______CD(后两空填“>”“<”或“=”).
2
<
>
知4-练
如图 6.2-29 所示,AC=8 cm,CB=6 cm,如果 O 是线段AB的中点,求线段OC的长度.
例 8
知4-练
思路引导:
知4-练
解:因为AB=AC+CB=8+6-14(cm),
O是线段AB的中点,所以AO=OB===7(cm),
所以OC=OB-CB=7-6=1(cm).
另解
OC=AC-AO=8-7=1(cm).
知4-练
素养点拨:本题以线段的中点为主要考点进行了线段的和差计算,进一步体会线段的和差与线段长度和差的关系,领悟数的运算策略和方法在数量运算中的运用,培养了运算能力.
知4-练
8-1.[新考法 分类讨论法]已知线 段 AC 和线 段BC 在同一直线上,如果AC=6 cm,BC=4 cm,则线段 AC 的中点和线段 BC 的中点之间的距离为______cm.
1或5
线段的比较与运算
线段的比较与运算
线段的比较
线段的运算
度量法
叠合法
线段的和差
线段的中点
同课章节目录
