24.3 锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 24.3 锐角三角函数 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:04:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.3 锐角三角函数
一、单选题
1.(2023九上·湖南月考)若,则的度数为( )
A.60° B.45° C.30° D.90°
2.(2023·龙马潭模拟)如图,在中,于,于,若,,,则的面积为( )
A.24 B.36 C.40 D.48
3.(2023九上·莲池期末)在中,若,则这个三角形一定是( )
A.直角三角形 B.等腰三角形 C.钝角三角形 D.锐角三角形
4.(2023九上·南阳月考)在中,若,则的余角度数是( )
A. B. C. D.
5.(2019·鹿城模拟)如图,在△ABC中,∠C=90°,AB=10,BC=6,则sin∠A=( )
A. B. C. D.
6.(2021九上·永年期中)下列计算错误的有( )
① ;② ;③ ;④ .
A.1个 B.2个 C.3个 D.4个
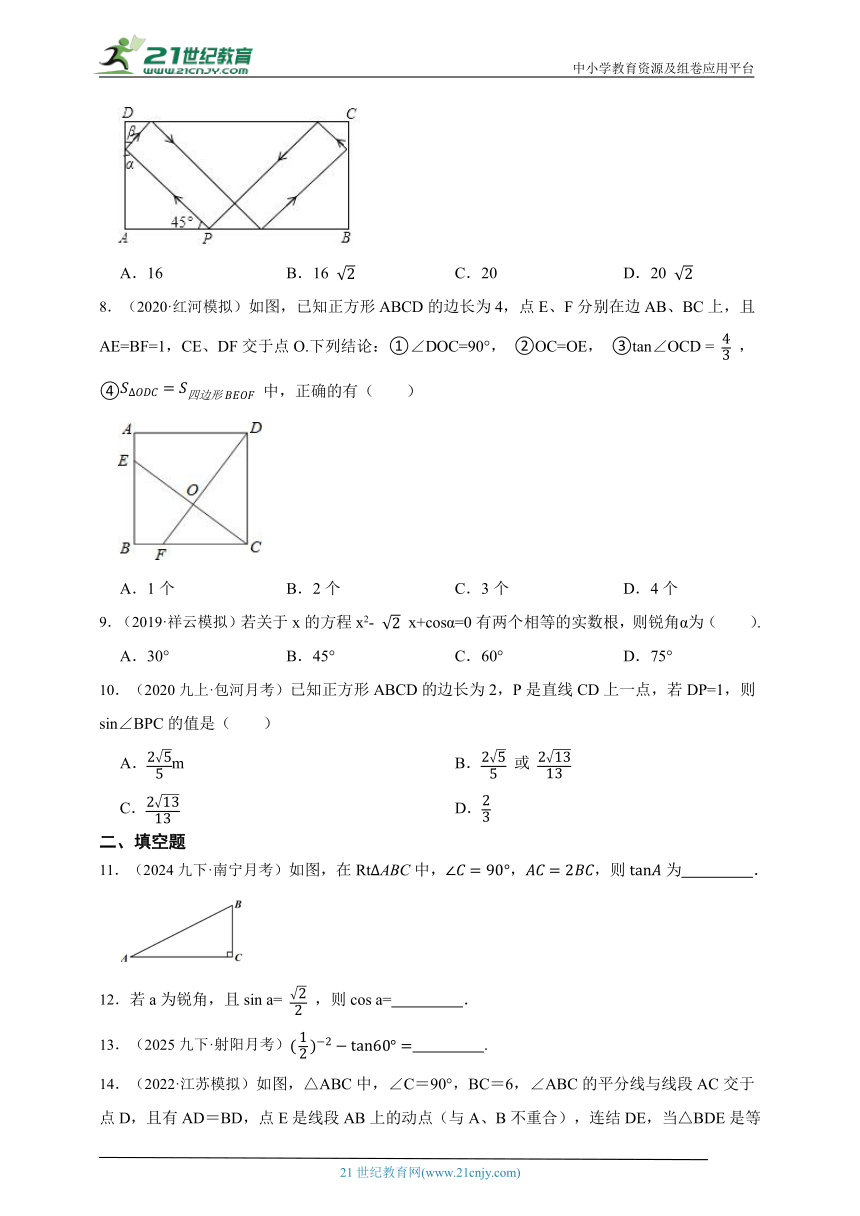
7.(2017·孝义模拟)如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
A.16 B.16 C.20 D.20
8.(2020·红河模拟)如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(2019·祥云模拟)若关于x的方程x2- x+cosα=0有两个相等的实数根,则锐角α为( ).
A.30° B.45° C.60° D.75°
10.(2020九上·包河月考)已知正方形ABCD的边长为2,P是直线CD上一点,若DP=1,则sin∠BPC的值是( )
A.m B. 或
C. D.
二、填空题
11.(2024九下·南宁月考)如图,在RtABC中,,,则为 .
12.若a为锐角,且sin a= ,则cos a= .
13.(2025九下·射阳月考) .
14.(2022·江苏模拟)如图,△ABC中,∠C=90°,BC=6,∠ABC的平分线与线段AC交于点D,且有AD=BD,点E是线段AB上的动点(与A、B不重合),连结DE,当△BDE是等腰三角形时,则AE的长为 .
15.(2023九上·曲阜期末)在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin = .
16.(2022·费县模拟)如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
三、计算题
17.(2024九下·松山模拟)计算:
.
18.(2019·梁平模拟)先化简,再求值: ,其中a=2cos30°﹣tan45°.
四、解答题
19.(2022九下·石家庄模拟)已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
20.(2024九上·定边期末)如图,在中,,,,求的值.
21.已知sin A=0.328 6,tan B=10.08,利用计算器求锐角A,B.(结果精确到0.01°)
22.(2024九上·任城月考)我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).如图,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°=________;
(2)如图②,已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
答案解析部分
1.【答案】A
【知识点】求特殊角的三角函数值
2.【答案】D
【知识点】平行四边形的性质;求特殊角的三角函数值
3.【答案】B
【知识点】等腰三角形的判定与性质;求特殊角的三角函数值
4.【答案】B
【知识点】余角、补角及其性质;三角形内角和定理;求特殊角的三角函数值;绝对值的非负性
5.【答案】A
【知识点】锐角三角函数的定义
6.【答案】C
【知识点】求特殊角的三角函数值
7.【答案】B
【知识点】锐角三角函数的定义
8.【答案】C
【知识点】全等三角形的判定与性质;正方形的性质;锐角三角函数的定义
9.【答案】C
【知识点】一元二次方程根的判别式及应用;求特殊角的三角函数值
10.【答案】B
【知识点】勾股定理;正方形的性质;锐角三角函数的定义
11.【答案】
【知识点】锐角三角函数的定义
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】负整数指数幂;求特殊角的三角函数值
14.【答案】 或
【知识点】三角形内角和定理;等腰三角形的性质;含30°角的直角三角形;勾股定理;锐角三角函数的定义
15.【答案】
【知识点】求特殊角的三角函数值
16.【答案】①②④
【知识点】多边形内角与外角;矩形的性质;锐角三角函数的定义;三角形全等的判定-AAS
17.【答案】10
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
18.【答案】解:原式= ÷( )
= ,
∵a=2cos30°﹣tan45°
∴原式=﹣ =﹣ .
【知识点】分式的化简求值;求特殊角的三角函数值
19.【答案】(1),,
(2)
【知识点】三角形内角和定理;勾股定理;求特殊角的三角函数值;绝对值的非负性
20.【答案】解:在中,,,,
由勾股定理得.
则
【知识点】锐角三角函数的定义
21.【答案】解:在计算器中运用表示“反三角函数”的按键,如“arcsin”或“sin-1”,“arctan”或“tan-1”,
分别计算得∠A≈19.18°,∠B≈84.33°。
【知识点】计算器—三角函数
22.【答案】(1);(2)18.
【知识点】锐角三角函数的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.3 锐角三角函数
一、单选题
1.(2023九上·湖南月考)若,则的度数为( )
A.60° B.45° C.30° D.90°
2.(2023·龙马潭模拟)如图,在中,于,于,若,,,则的面积为( )
A.24 B.36 C.40 D.48
3.(2023九上·莲池期末)在中,若,则这个三角形一定是( )
A.直角三角形 B.等腰三角形 C.钝角三角形 D.锐角三角形
4.(2023九上·南阳月考)在中,若,则的余角度数是( )
A. B. C. D.
5.(2019·鹿城模拟)如图,在△ABC中,∠C=90°,AB=10,BC=6,则sin∠A=( )
A. B. C. D.
6.(2021九上·永年期中)下列计算错误的有( )
① ;② ;③ ;④ .
A.1个 B.2个 C.3个 D.4个
7.(2017·孝义模拟)如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )
A.16 B.16 C.20 D.20
8.(2020·红河模拟)如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(2019·祥云模拟)若关于x的方程x2- x+cosα=0有两个相等的实数根,则锐角α为( ).
A.30° B.45° C.60° D.75°
10.(2020九上·包河月考)已知正方形ABCD的边长为2,P是直线CD上一点,若DP=1,则sin∠BPC的值是( )
A.m B. 或
C. D.
二、填空题
11.(2024九下·南宁月考)如图,在RtABC中,,,则为 .
12.若a为锐角,且sin a= ,则cos a= .
13.(2025九下·射阳月考) .
14.(2022·江苏模拟)如图,△ABC中,∠C=90°,BC=6,∠ABC的平分线与线段AC交于点D,且有AD=BD,点E是线段AB上的动点(与A、B不重合),连结DE,当△BDE是等腰三角形时,则AE的长为 .
15.(2023九上·曲阜期末)在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin = .
16.(2022·费县模拟)如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
三、计算题
17.(2024九下·松山模拟)计算:
.
18.(2019·梁平模拟)先化简,再求值: ,其中a=2cos30°﹣tan45°.
四、解答题
19.(2022九下·石家庄模拟)已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
20.(2024九上·定边期末)如图,在中,,,,求的值.
21.已知sin A=0.328 6,tan B=10.08,利用计算器求锐角A,B.(结果精确到0.01°)
22.(2024九上·任城月考)我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).如图,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°=________;
(2)如图②,已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
答案解析部分
1.【答案】A
【知识点】求特殊角的三角函数值
2.【答案】D
【知识点】平行四边形的性质;求特殊角的三角函数值
3.【答案】B
【知识点】等腰三角形的判定与性质;求特殊角的三角函数值
4.【答案】B
【知识点】余角、补角及其性质;三角形内角和定理;求特殊角的三角函数值;绝对值的非负性
5.【答案】A
【知识点】锐角三角函数的定义
6.【答案】C
【知识点】求特殊角的三角函数值
7.【答案】B
【知识点】锐角三角函数的定义
8.【答案】C
【知识点】全等三角形的判定与性质;正方形的性质;锐角三角函数的定义
9.【答案】C
【知识点】一元二次方程根的判别式及应用;求特殊角的三角函数值
10.【答案】B
【知识点】勾股定理;正方形的性质;锐角三角函数的定义
11.【答案】
【知识点】锐角三角函数的定义
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】负整数指数幂;求特殊角的三角函数值
14.【答案】 或
【知识点】三角形内角和定理;等腰三角形的性质;含30°角的直角三角形;勾股定理;锐角三角函数的定义
15.【答案】
【知识点】求特殊角的三角函数值
16.【答案】①②④
【知识点】多边形内角与外角;矩形的性质;锐角三角函数的定义;三角形全等的判定-AAS
17.【答案】10
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
18.【答案】解:原式= ÷( )
= ,
∵a=2cos30°﹣tan45°
∴原式=﹣ =﹣ .
【知识点】分式的化简求值;求特殊角的三角函数值
19.【答案】(1),,
(2)
【知识点】三角形内角和定理;勾股定理;求特殊角的三角函数值;绝对值的非负性
20.【答案】解:在中,,,,
由勾股定理得.
则
【知识点】锐角三角函数的定义
21.【答案】解:在计算器中运用表示“反三角函数”的按键,如“arcsin”或“sin-1”,“arctan”或“tan-1”,
分别计算得∠A≈19.18°,∠B≈84.33°。
【知识点】计算器—三角函数
22.【答案】(1);(2)18.
【知识点】锐角三角函数的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
