24.3.1锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 24.3.1锐角三角函数 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:05:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.锐角三角函数
一、单选题
1.(2024九上·路北期末)已知 为锐角,且 ,则 的值是( )
A. B. C. D.
2.(2024九上·宣化期中)的倒数是( )
A. B. C.2 D.
3.(2018九上·垣曲期末)cos60°的值为( )
A. B. C. D.
4.(2020·河西模拟) 的值等于( )
A. B.1 C. D.
5.在Rt△ABC,∠C=90°,AC=12,BC=5,则sinA的值为( )
A. B. C. D.
6.(2023九上·江北期末)如图,在中,,,,则( )
A. B. C.4 D.
7.以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为 ( )
A.(cosα, 1) B.(1, sinα)
C.(cosα, sinα) D.(sinα, cosα)
8.在△ABC中,∠A=120°,∠B=45°,∠C=15°,则cosB等于( )
A. B. C. D.
9.(2018·黄冈)下列运算结果正确的是( )
A.3a3·2a2=6a6 B.(-2a)2= -4a2
C.tan45°= D.cos30°=
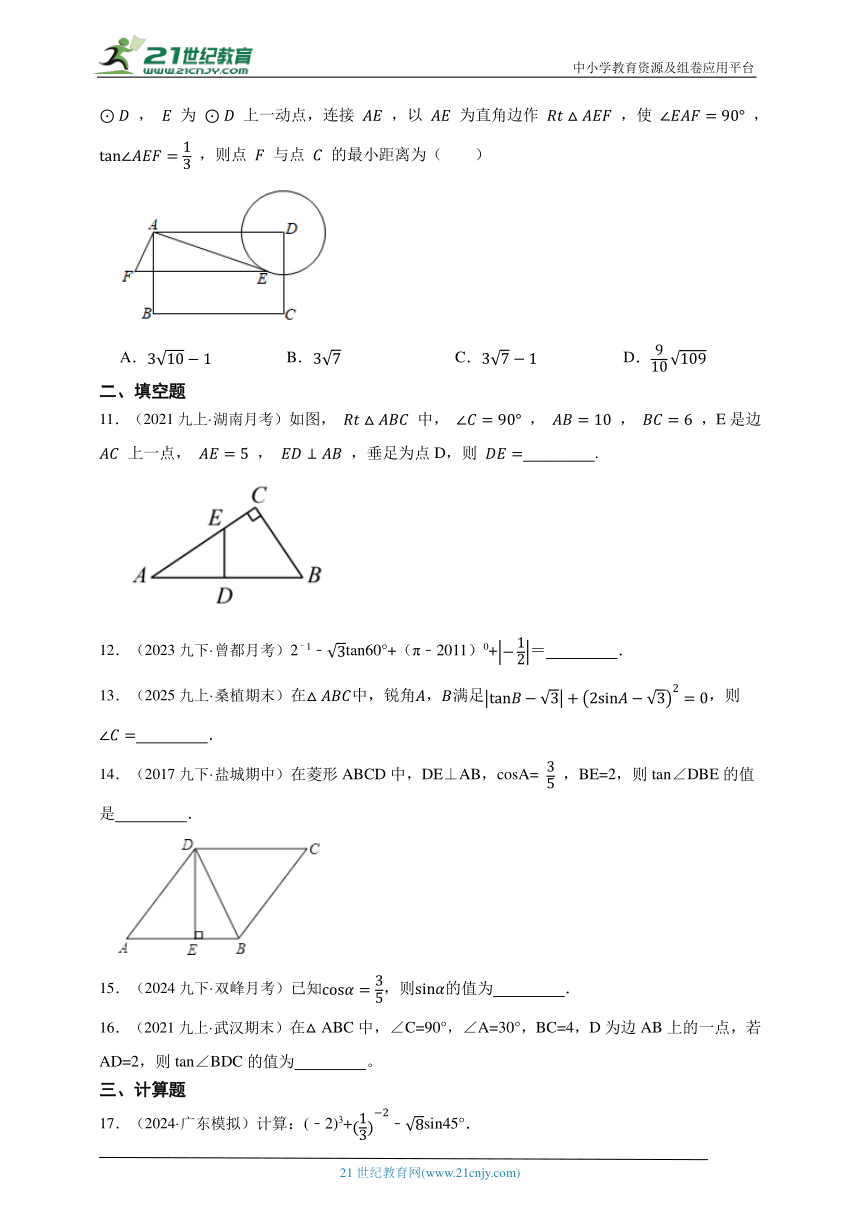
10.(2021·苏州模拟)如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )
A. B. C. D.
二、填空题
11.(2021九上·湖南月考)如图, 中, , , ,E是边 上一点, , ,垂足为点D,则 .
12.(2023九下·曾都月考)2﹣1﹣tan60°+(π﹣2011)0+= .
13.(2025九上·桑植期末)在中,锐角,满足,则 .
14.(2017九下·盐城期中)在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则tan∠DBE的值是 .
15.(2024九下·双峰月考)已知,则的值为 .
16.(2021九上·武汉期末)在△ABC中,∠C=90°,∠A=30°,BC=4,D为边AB上的一点,若AD=2,则tan∠BDC的值为 。
三、计算题
17.(2024·广东模拟)计算:(﹣2)3+﹣sin45°.
18.(2025·凉州模拟)计算:
四、解答题
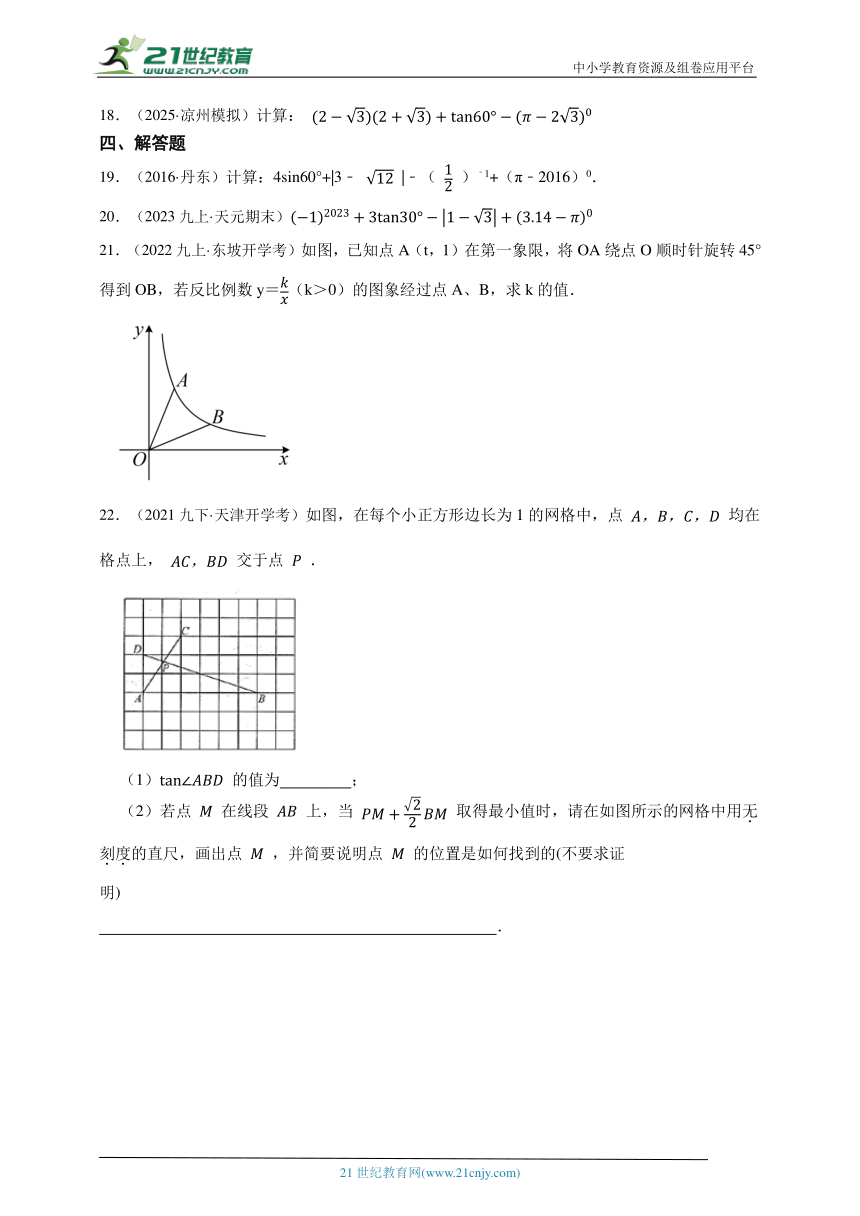
19.(2016·丹东)计算:4sin60°+|3﹣ |﹣( )﹣1+(π﹣2016)0.
20.(2023九上·天元期末)
21.(2022九上·东坡开学考)如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=(k>0)的图象经过点A、B,求k的值.
22.(2021九下·天津开学考)如图,在每个小正方形边长为1的网格中,点 均在格点上, 交于点 .
(1) 的值为 ;
(2)若点 在线段 上,当 取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
答案解析部分
1.【答案】A
【知识点】求特殊角的三角函数值
2.【答案】C
【知识点】有理数的倒数;求特殊角的三角函数值
3.【答案】A
【知识点】求特殊角的三角函数值
4.【答案】B
【知识点】求特殊角的三角函数值
5.【答案】D
【知识点】锐角三角函数的定义
6.【答案】B
【知识点】勾股定理;锐角三角函数的定义
7.【答案】C
【知识点】锐角三角函数的定义
8.【答案】D
【知识点】求特殊角的三角函数值
9.【答案】D
【知识点】单项式乘单项式;求特殊角的三角函数值;积的乘方运算
10.【答案】A
【知识点】两点之间线段最短;矩形的性质;相似三角形的判定与性质;锐角三角函数的定义
11.【答案】3
【知识点】锐角三角函数的定义
12.【答案】-1
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】求特殊角的三角函数值;绝对值的非负性
14.【答案】2
【知识点】菱形的性质;锐角三角函数的定义
15.【答案】
【知识点】同角三角函数的关系
16.【答案】
【知识点】含30°角的直角三角形;锐角三角函数的定义
17.【答案】-1.
【知识点】负整数指数幂;求特殊角的三角函数值
18.【答案】解:原式
.
【知识点】实数的运算;求特殊角的三角函数值
19.【答案】解:4sin60°+|3﹣ |﹣( )﹣1+(π﹣2016)0
=4× +2 ﹣3﹣2+1
=2 +2 ﹣4
=4 ﹣4
【知识点】实数的运算;零指数幂;负整数指数幂;求特殊角的三角函数值
20.【答案】1
【知识点】零指数幂;求特殊角的三角函数值
21.【答案】解:如图,点A(t,1),将OA绕点O顺时针旋转45°得到OB,
根据反比例函数图象关于直线y=x的对称性得,
B(1,t),
过点A作AC⊥y轴于点C,BE⊥x轴于点E,
又由k的几何意义可知:
k=1×t=t,
∵∠AOB=45°,
∴∠AOC=∠BOE=22.5°,
∴tan∠AOC=tan22.5°==t=k,
在OC上取一点,使得AC=CD=t,
则有△ACD为等腰直角三角形,∠ADC=45°
∴∠DAO=∠DOA=22.5°,
∴AD=OD,
∴AD=DO=t,
∴OC=OD+DC=t+t,
即1=t+t,
解得t=-1.
所以k=-1.
【知识点】反比例函数系数k的几何意义;锐角三角函数的定义
22.【答案】(1)
(2)取格点 ,连接 与 相交,得点 .连接 ,与 相交,得点 ,点 即为所求, .
【知识点】锐角三角函数的定义;尺规作图的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.锐角三角函数
一、单选题
1.(2024九上·路北期末)已知 为锐角,且 ,则 的值是( )
A. B. C. D.
2.(2024九上·宣化期中)的倒数是( )
A. B. C.2 D.
3.(2018九上·垣曲期末)cos60°的值为( )
A. B. C. D.
4.(2020·河西模拟) 的值等于( )
A. B.1 C. D.
5.在Rt△ABC,∠C=90°,AC=12,BC=5,则sinA的值为( )
A. B. C. D.
6.(2023九上·江北期末)如图,在中,,,,则( )
A. B. C.4 D.
7.以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为 ( )
A.(cosα, 1) B.(1, sinα)
C.(cosα, sinα) D.(sinα, cosα)
8.在△ABC中,∠A=120°,∠B=45°,∠C=15°,则cosB等于( )
A. B. C. D.
9.(2018·黄冈)下列运算结果正确的是( )
A.3a3·2a2=6a6 B.(-2a)2= -4a2
C.tan45°= D.cos30°=
10.(2021·苏州模拟)如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )
A. B. C. D.
二、填空题
11.(2021九上·湖南月考)如图, 中, , , ,E是边 上一点, , ,垂足为点D,则 .
12.(2023九下·曾都月考)2﹣1﹣tan60°+(π﹣2011)0+= .
13.(2025九上·桑植期末)在中,锐角,满足,则 .
14.(2017九下·盐城期中)在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则tan∠DBE的值是 .
15.(2024九下·双峰月考)已知,则的值为 .
16.(2021九上·武汉期末)在△ABC中,∠C=90°,∠A=30°,BC=4,D为边AB上的一点,若AD=2,则tan∠BDC的值为 。
三、计算题
17.(2024·广东模拟)计算:(﹣2)3+﹣sin45°.
18.(2025·凉州模拟)计算:
四、解答题
19.(2016·丹东)计算:4sin60°+|3﹣ |﹣( )﹣1+(π﹣2016)0.
20.(2023九上·天元期末)
21.(2022九上·东坡开学考)如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=(k>0)的图象经过点A、B,求k的值.
22.(2021九下·天津开学考)如图,在每个小正方形边长为1的网格中,点 均在格点上, 交于点 .
(1) 的值为 ;
(2)若点 在线段 上,当 取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
答案解析部分
1.【答案】A
【知识点】求特殊角的三角函数值
2.【答案】C
【知识点】有理数的倒数;求特殊角的三角函数值
3.【答案】A
【知识点】求特殊角的三角函数值
4.【答案】B
【知识点】求特殊角的三角函数值
5.【答案】D
【知识点】锐角三角函数的定义
6.【答案】B
【知识点】勾股定理;锐角三角函数的定义
7.【答案】C
【知识点】锐角三角函数的定义
8.【答案】D
【知识点】求特殊角的三角函数值
9.【答案】D
【知识点】单项式乘单项式;求特殊角的三角函数值;积的乘方运算
10.【答案】A
【知识点】两点之间线段最短;矩形的性质;相似三角形的判定与性质;锐角三角函数的定义
11.【答案】3
【知识点】锐角三角函数的定义
12.【答案】-1
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】求特殊角的三角函数值;绝对值的非负性
14.【答案】2
【知识点】菱形的性质;锐角三角函数的定义
15.【答案】
【知识点】同角三角函数的关系
16.【答案】
【知识点】含30°角的直角三角形;锐角三角函数的定义
17.【答案】-1.
【知识点】负整数指数幂;求特殊角的三角函数值
18.【答案】解:原式
.
【知识点】实数的运算;求特殊角的三角函数值
19.【答案】解:4sin60°+|3﹣ |﹣( )﹣1+(π﹣2016)0
=4× +2 ﹣3﹣2+1
=2 +2 ﹣4
=4 ﹣4
【知识点】实数的运算;零指数幂;负整数指数幂;求特殊角的三角函数值
20.【答案】1
【知识点】零指数幂;求特殊角的三角函数值
21.【答案】解:如图,点A(t,1),将OA绕点O顺时针旋转45°得到OB,
根据反比例函数图象关于直线y=x的对称性得,
B(1,t),
过点A作AC⊥y轴于点C,BE⊥x轴于点E,
又由k的几何意义可知:
k=1×t=t,
∵∠AOB=45°,
∴∠AOC=∠BOE=22.5°,
∴tan∠AOC=tan22.5°==t=k,
在OC上取一点,使得AC=CD=t,
则有△ACD为等腰直角三角形,∠ADC=45°
∴∠DAO=∠DOA=22.5°,
∴AD=OD,
∴AD=DO=t,
∴OC=OD+DC=t+t,
即1=t+t,
解得t=-1.
所以k=-1.
【知识点】反比例函数系数k的几何意义;锐角三角函数的定义
22.【答案】(1)
(2)取格点 ,连接 与 相交,得点 .连接 ,与 相交,得点 ,点 即为所求, .
【知识点】锐角三角函数的定义;尺规作图的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
