25.2.2 频率与概率 同步练习(含答案)
文档属性
| 名称 | 25.2.2 频率与概率 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 405.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:14:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.频率与概率
一、单选题
1.(2024九上·方城期末)某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,则符合这一结果的实验最有可能的是( )
A.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.掷一枚质地均匀的硬币,落地时结果是“正面向上”
2.(2023九上·郑州经济技术开发期中)在一个不透明的袋子中有除颜色外其他均相同的个黑球、个白球和若干个红球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中.通过大量重复摸球试验后,发现摸到红球的频率稳定于,由此可以估计袋中红球的个数约为( )
A. B. C. D.
3.(2023九上·永修期中) 数学兴趣小组做“任意抛掷一枚图钉”的重复试验, 多次试验后获得如下数据:
重复试验次数 10 50 100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为( )
A. B. C. D.
4.(2023九上·兴隆台期末)不透明的盒子中装有红、黄色的小球共个,除颜色外无其他差别,随机摸出一个小球,记录颜色后放回并摇匀,再随机摸出一个.如图显示了某数学小组开展上述摸球活动的某次实验的结果.
下面有四个推断:
①当摸球次数是时,记录“摸到红球”的次数是,所以“摸到红球”的概率是;
②随着试验次数的增加,“摸到红球”的频率总在附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是;
③可以根据本次实验结果,计算出盒子中约有红球个;
④若再次开展上述摸球活动,则当摸球次数为时,“摸到红球”的频率一定是.
所有合理推断的序号是( )
A.①② B.②③ C.①②③ D.②③④
5.(2025九上·通山期末)用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为,是指( )
A.连续抛掷次必有次正面朝上
B.连续抛掷次不可能正面都朝上
C.大量反复抛掷每次出现正面朝上次
D.抛掷次,当越来越大时,正面朝上的频率会越来越稳定于
6.在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是 ”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( ).
A.0个 B.1个 C.2个 D.3个
7.已知一口袋中放有红、白、黑三种颜色的球共50个,它们除颜色外其他都一样,一位同学通过多次试验后发现摸到红、白色的频率基本稳定是45%和15%,则袋中黑球的个数可能是( )
A.16 B.18 C.20 D.22
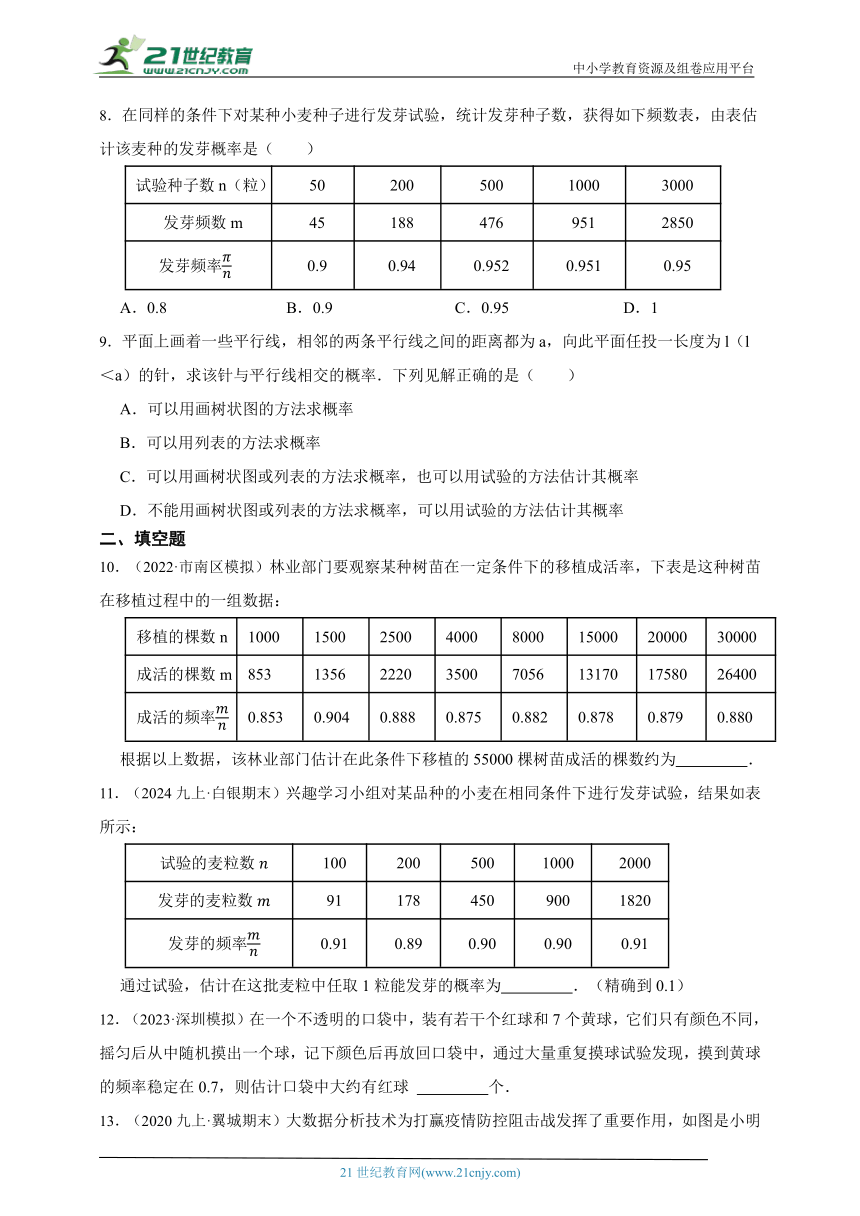
8.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A.0.8 B.0.9 C.0.95 D.1
9.平面上画着一些平行线,相邻的两条平行线之间的距离都为a,向此平面任投一长度为l(l<a)的针,求该针与平行线相交的概率.下列见解正确的是( )
A.可以用画树状图的方法求概率
B.可以用列表的方法求概率
C.可以用画树状图或列表的方法求概率,也可以用试验的方法估计其概率
D.不能用画树状图或列表的方法求概率,可以用试验的方法估计其概率
二、填空题
10.(2022·市南区模拟)林业部门要观察某种树苗在一定条件下的移植成活率,下表是这种树苗在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 853 1356 2220 3500 7056 13170 17580 26400
成活的频率 0.853 0.904 0.888 0.875 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为 .
11.(2024九上·白银期末)兴趣学习小组对某品种的小麦在相同条件下进行发芽试验,结果如表所示:
试验的麦粒数 100 200 500 1000 2000
发芽的麦粒数 91 178 450 900 1820
发芽的频率 0.91 0.89 0.90 0.90 0.91
通过试验,估计在这批麦粒中任取1粒能发芽的概率为 .(精确到0.1)
12.(2023·深圳模拟)在一个不透明的口袋中,装有若干个红球和7个黄球,它们只有颜色不同,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率稳定在0.7,则估计口袋中大约有红球 个.
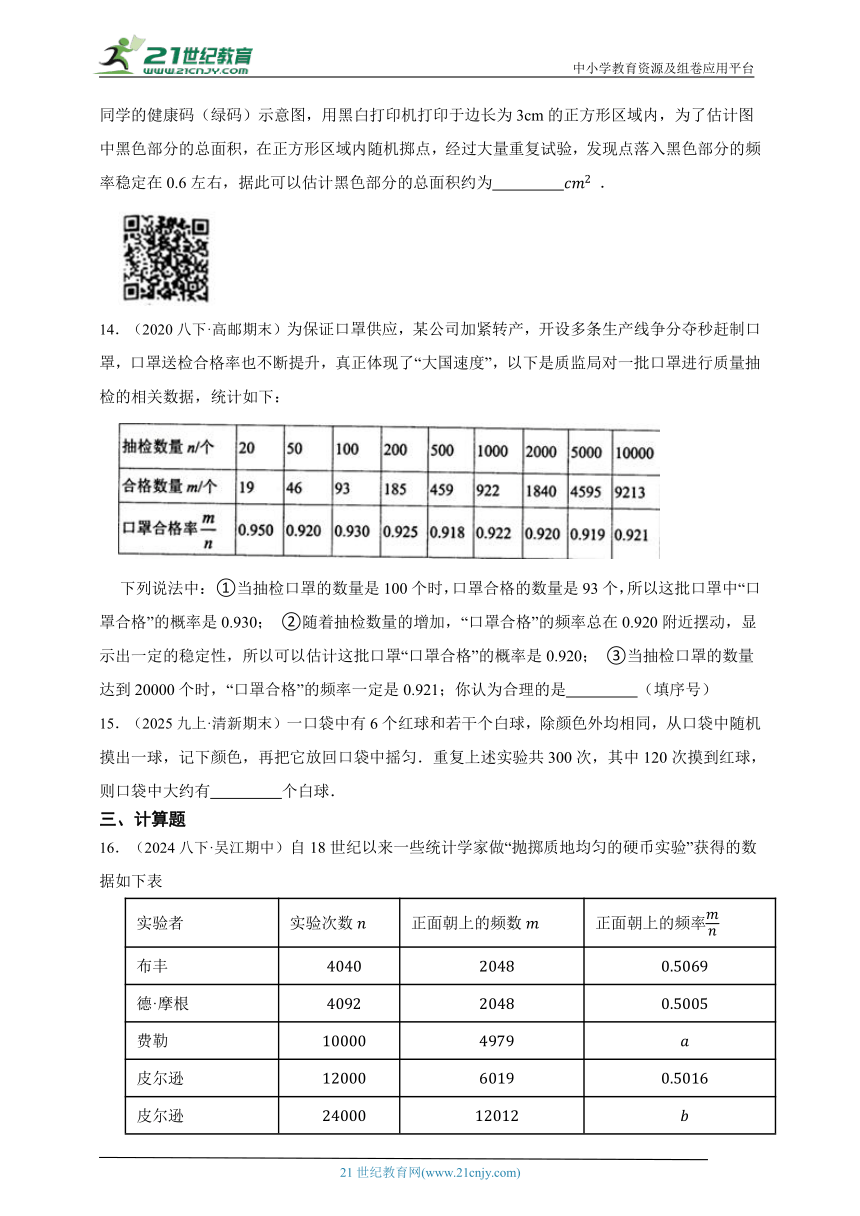
13.(2020九上·翼城期末)大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为3cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
14.(2020八下·高邮期末)为保证口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,口罩送检合格率也不断提升,真正体现了“大国速度”,以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
下列说法中: ①当抽检口罩的数量是100个时,口罩合格的数量是93个,所以这批口罩中“口罩合格”的概率是0.930; ②随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩“口罩合格”的概率是0.920; ③当抽检口罩的数量达到20000个时,“口罩合格”的频率一定是0.921;你认为合理的是 (填序号)
15.(2025九上·清新期末)一口袋中有6个红球和若干个白球,除颜色外均相同,从口袋中随机摸出一球,记下颜色,再把它放回口袋中摇匀.重复上述实验共300次,其中120次摸到红球,则口袋中大约有 个白球.
三、计算题
16.(2024八下·吴江期中)自18世纪以来一些统计学家做“抛掷质地均匀的硬币实验”获得的数据如下表
实验者 实验次数 正面朝上的频数 正面朝上的频率
布丰
德·摩根
费勒
皮尔逊
皮尔逊
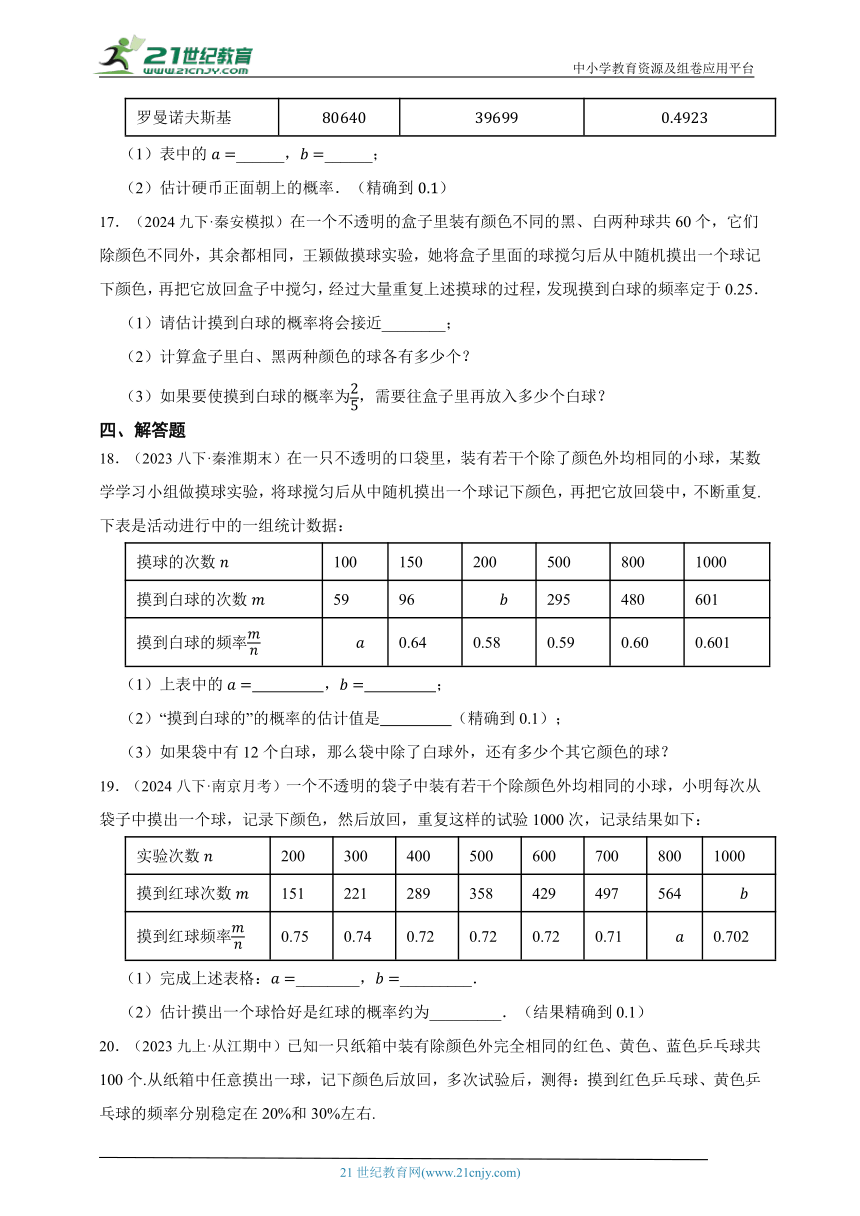
罗曼诺夫斯基
(1)表中的______,______;
(2)估计硬币正面朝上的概率.(精确到)
17.(2024九下·秦安模拟)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于0.25.
(1)请估计摸到白球的概率将会接近________;
(2)计算盒子里白、黑两种颜色的球各有多少个?
(3)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
四、解答题
18.(2023八下·秦淮期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 59 96 295 480 601
摸到白球的频率 0.64 0.58 0.59 0.60 0.601
(1)上表中的 , ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
19.(2024八下·南京月考)一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数 200 300 400 500 600 700 800 1000
摸到红球次数 151 221 289 358 429 497 564
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 0.702
(1)完成上述表格:________,_________.
(2)估计摸出一个球恰好是红球的概率约为_________.(结果精确到0.1)
20.(2023九上·从江期中)已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,记下颜色后放回,多次试验后,测得:摸到红色乒乓球、黄色乒乓球的频率分别稳定在20%和30%左右.
(1)试求出纸箱中蓝色乒乓球的个数;
(2)假设向纸箱中再放进红色乒乓球x个,这时从纸箱中任意取出一个球是红色乒乓球的概率为0.5,试求x的值.
21.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 2 5 6 4 10 3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】A
【知识点】利用频率估计概率
3.【答案】B
【知识点】利用频率估计概率
4.【答案】B
【知识点】利用频率估计概率
5.【答案】D
【知识点】利用频率估计概率
6.【答案】A
【知识点】利用频率估计概率
7.【答案】C
【知识点】利用频率估计概率
8.【答案】C
【知识点】利用频率估计概率
9.【答案】D
【知识点】利用频率估计概率
10.【答案】48400
【知识点】利用频率估计概率
11.【答案】0.9
【知识点】利用频率估计概率
12.【答案】3
【知识点】利用频率估计概率
13.【答案】5.4
【知识点】利用频率估计概率
14.【答案】②
【知识点】概率的意义;利用频率估计概率
15.【答案】9
【知识点】利用频率估计概率
16.【答案】(1);
(2)
【知识点】频数与频率;利用频率估计概率
17.【答案】(1)0.25;(2)盒子里白、黑两种颜色的球各有15个、45个;(3)15
【知识点】利用频率估计概率
18.【答案】(1)0.59;116
(2)0.6
(3)解:(个).答:除白球外,还有大约8个其它颜色的小球.
【知识点】利用频率估计概率
19.【答案】(1)0.705,702
(2)0.7
【知识点】利用频率估计概率
20.【答案】(1)解:纸箱中蓝色乒乓球有
100×(1-20%-30%)=50(个).
(2)解:原来纸箱中红色乒乓球有100×20%=20(个),
向纸箱中再放进红色乒乓球x个,任取一个球是红色球的概率是0.5,则=0.5,解得x=60.经检验,x=60是原方程的解,即x的值为60.
【知识点】利用频率估计概率;概率的简单应用
21.【答案】解:(1)“3点朝上”的频率为:,
“5点朝上”的频率为:;
(2)王勇的说法是错误的
因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,
只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率.
李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次.
(3)列表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵朝上的点数之和为3的倍数共有12个,
∴P(点数之和为3的倍数)= .
【知识点】利用频率估计概率
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.频率与概率
一、单选题
1.(2024九上·方城期末)某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,则符合这一结果的实验最有可能的是( )
A.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.掷一枚质地均匀的硬币,落地时结果是“正面向上”
2.(2023九上·郑州经济技术开发期中)在一个不透明的袋子中有除颜色外其他均相同的个黑球、个白球和若干个红球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中.通过大量重复摸球试验后,发现摸到红球的频率稳定于,由此可以估计袋中红球的个数约为( )
A. B. C. D.
3.(2023九上·永修期中) 数学兴趣小组做“任意抛掷一枚图钉”的重复试验, 多次试验后获得如下数据:
重复试验次数 10 50 100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意抛掷一次图钉,钉尖朝上的概率约为( )
A. B. C. D.
4.(2023九上·兴隆台期末)不透明的盒子中装有红、黄色的小球共个,除颜色外无其他差别,随机摸出一个小球,记录颜色后放回并摇匀,再随机摸出一个.如图显示了某数学小组开展上述摸球活动的某次实验的结果.
下面有四个推断:
①当摸球次数是时,记录“摸到红球”的次数是,所以“摸到红球”的概率是;
②随着试验次数的增加,“摸到红球”的频率总在附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是;
③可以根据本次实验结果,计算出盒子中约有红球个;
④若再次开展上述摸球活动,则当摸球次数为时,“摸到红球”的频率一定是.
所有合理推断的序号是( )
A.①② B.②③ C.①②③ D.②③④
5.(2025九上·通山期末)用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为,是指( )
A.连续抛掷次必有次正面朝上
B.连续抛掷次不可能正面都朝上
C.大量反复抛掷每次出现正面朝上次
D.抛掷次,当越来越大时,正面朝上的频率会越来越稳定于
6.在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是 ”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( ).
A.0个 B.1个 C.2个 D.3个
7.已知一口袋中放有红、白、黑三种颜色的球共50个,它们除颜色外其他都一样,一位同学通过多次试验后发现摸到红、白色的频率基本稳定是45%和15%,则袋中黑球的个数可能是( )
A.16 B.18 C.20 D.22
8.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A.0.8 B.0.9 C.0.95 D.1
9.平面上画着一些平行线,相邻的两条平行线之间的距离都为a,向此平面任投一长度为l(l<a)的针,求该针与平行线相交的概率.下列见解正确的是( )
A.可以用画树状图的方法求概率
B.可以用列表的方法求概率
C.可以用画树状图或列表的方法求概率,也可以用试验的方法估计其概率
D.不能用画树状图或列表的方法求概率,可以用试验的方法估计其概率
二、填空题
10.(2022·市南区模拟)林业部门要观察某种树苗在一定条件下的移植成活率,下表是这种树苗在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 853 1356 2220 3500 7056 13170 17580 26400
成活的频率 0.853 0.904 0.888 0.875 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为 .
11.(2024九上·白银期末)兴趣学习小组对某品种的小麦在相同条件下进行发芽试验,结果如表所示:
试验的麦粒数 100 200 500 1000 2000
发芽的麦粒数 91 178 450 900 1820
发芽的频率 0.91 0.89 0.90 0.90 0.91
通过试验,估计在这批麦粒中任取1粒能发芽的概率为 .(精确到0.1)
12.(2023·深圳模拟)在一个不透明的口袋中,装有若干个红球和7个黄球,它们只有颜色不同,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率稳定在0.7,则估计口袋中大约有红球 个.
13.(2020九上·翼城期末)大数据分析技术为打赢疫情防控阻击战发挥了重要作用,如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为3cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
14.(2020八下·高邮期末)为保证口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,口罩送检合格率也不断提升,真正体现了“大国速度”,以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
下列说法中: ①当抽检口罩的数量是100个时,口罩合格的数量是93个,所以这批口罩中“口罩合格”的概率是0.930; ②随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩“口罩合格”的概率是0.920; ③当抽检口罩的数量达到20000个时,“口罩合格”的频率一定是0.921;你认为合理的是 (填序号)
15.(2025九上·清新期末)一口袋中有6个红球和若干个白球,除颜色外均相同,从口袋中随机摸出一球,记下颜色,再把它放回口袋中摇匀.重复上述实验共300次,其中120次摸到红球,则口袋中大约有 个白球.
三、计算题
16.(2024八下·吴江期中)自18世纪以来一些统计学家做“抛掷质地均匀的硬币实验”获得的数据如下表
实验者 实验次数 正面朝上的频数 正面朝上的频率
布丰
德·摩根
费勒
皮尔逊
皮尔逊
罗曼诺夫斯基
(1)表中的______,______;
(2)估计硬币正面朝上的概率.(精确到)
17.(2024九下·秦安模拟)在一个不透明的盒子里装有颜色不同的黑、白两种球共60个,它们除颜色不同外,其余都相同,王颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于0.25.
(1)请估计摸到白球的概率将会接近________;
(2)计算盒子里白、黑两种颜色的球各有多少个?
(3)如果要使摸到白球的概率为,需要往盒子里再放入多少个白球?
四、解答题
18.(2023八下·秦淮期末)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 100 150 200 500 800 1000
摸到白球的次数 59 96 295 480 601
摸到白球的频率 0.64 0.58 0.59 0.60 0.601
(1)上表中的 , ;
(2)“摸到白球的”的概率的估计值是 (精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
19.(2024八下·南京月考)一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数 200 300 400 500 600 700 800 1000
摸到红球次数 151 221 289 358 429 497 564
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 0.702
(1)完成上述表格:________,_________.
(2)估计摸出一个球恰好是红球的概率约为_________.(结果精确到0.1)
20.(2023九上·从江期中)已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,记下颜色后放回,多次试验后,测得:摸到红色乒乓球、黄色乒乓球的频率分别稳定在20%和30%左右.
(1)试求出纸箱中蓝色乒乓球的个数;
(2)假设向纸箱中再放进红色乒乓球x个,这时从纸箱中任意取出一个球是红色乒乓球的概率为0.5,试求x的值.
21.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 1 2 3 4 5 6
出现的次数 2 5 6 4 10 3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】A
【知识点】利用频率估计概率
3.【答案】B
【知识点】利用频率估计概率
4.【答案】B
【知识点】利用频率估计概率
5.【答案】D
【知识点】利用频率估计概率
6.【答案】A
【知识点】利用频率估计概率
7.【答案】C
【知识点】利用频率估计概率
8.【答案】C
【知识点】利用频率估计概率
9.【答案】D
【知识点】利用频率估计概率
10.【答案】48400
【知识点】利用频率估计概率
11.【答案】0.9
【知识点】利用频率估计概率
12.【答案】3
【知识点】利用频率估计概率
13.【答案】5.4
【知识点】利用频率估计概率
14.【答案】②
【知识点】概率的意义;利用频率估计概率
15.【答案】9
【知识点】利用频率估计概率
16.【答案】(1);
(2)
【知识点】频数与频率;利用频率估计概率
17.【答案】(1)0.25;(2)盒子里白、黑两种颜色的球各有15个、45个;(3)15
【知识点】利用频率估计概率
18.【答案】(1)0.59;116
(2)0.6
(3)解:(个).答:除白球外,还有大约8个其它颜色的小球.
【知识点】利用频率估计概率
19.【答案】(1)0.705,702
(2)0.7
【知识点】利用频率估计概率
20.【答案】(1)解:纸箱中蓝色乒乓球有
100×(1-20%-30%)=50(个).
(2)解:原来纸箱中红色乒乓球有100×20%=20(个),
向纸箱中再放进红色乒乓球x个,任取一个球是红色球的概率是0.5,则=0.5,解得x=60.经检验,x=60是原方程的解,即x的值为60.
【知识点】利用频率估计概率;概率的简单应用
21.【答案】解:(1)“3点朝上”的频率为:,
“5点朝上”的频率为:;
(2)王勇的说法是错误的
因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大,
只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率.
李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次.
(3)列表:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
∵朝上的点数之和为3的倍数共有12个,
∴P(点数之和为3的倍数)= .
【知识点】利用频率估计概率
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
