25.2.3 列举所有机会均等的结果 同步练习(含答案)
文档属性
| 名称 | 25.2.3 列举所有机会均等的结果 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 741.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.列举所有机会均等的结果
一、单选题
1.(2025九上·莆田期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
2.(2023九上·和平期末)为了调动同学们学习数学的积极性,班内组织开展了数学素养大赛,老师将三道题的题号1,2,3,分别写在完全相同的3张卡片的正面,将卡片背面朝上洗匀.小李先从中随机抽取一张卡片,记录下卡片上的数字后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的数字,则两张卡片上的数字是“1”和“3”的概率为( )
A. B. C. D.
3.(2016·余姚模拟)有3个整式x,x+1,2,先随机取一个整式作为分子,再在余下的整式中随机取一个作为分母,恰能组成成分式的概率是( )
A. B. C. D.
4.(2024九上·贵阳月考)如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
A. B. C. D.
5.(2024九下·新县模拟)据中国载人航天工程办公室消息,北京时间年月日,神舟十六号、神舟十七号航天员乘组进行交接仪式,两个乘组移交了中国空间站的钥匙.空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设“神舟十七号”的三名航天员“汤洪波、唐胜杰、江新林”从核心舱进入问天实验舱和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选人各进入一个实验舱开展科学实验,则汤洪波、唐胜杰两人同时被选中的概率为( )
A. B. C. D.
6.(2018九上·十堰期末)甲、乙、丙三人参加数学、物理、英语三项竞赛,每人限报一项,每项限报一人,则甲报英语、乙报数学、丙报物理的概率是( )
A. B. C. D.
7.(2017·河南模拟)用m,n,p,q四把钥匙去开A,B两把锁,其中仅有钥匙m能打开锁A,仅有钥匙n能打开锁B,则“取一把钥匙恰能打开一把锁”的概率是( )
A. B. C. D.
8.(2023九上·青秀期末)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界普为“中国第五大发明”,小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( )
A. B. C. D.
9.(2020九上·大石桥月考)小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
10.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( )
A. B. C. D.
二、填空题
11.(2025·曾都模拟)为发展学生的阅读素养,某校开设了《西游记》,《三国演义》,《水浒传》和《红楼梦》四个整本书阅读项目,小红随机抽取两个项目进行阅读,恰好抽到《西游记》和《红楼梦》阅读项目的概率是 .
12.(2020·南漳模拟)在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1,﹣2,3,4,随机摸取一个小球记下标号后放回,再随机摸取一个小球记下标号,则两次摸取的小球的标号之积为负数的概率为 .
13.(2023·巴中模拟)生物体的性状通常是由一对基因控制的,当控制某种性状的一对基因都是显性或一个是显性、一个是隐性时,生物体表现出显性基因控制的性状;当控制某种性状的基因都是隐性时,隐性基因控制的性状才会表现出来.在单、双眼皮的性状遗传中,双眼皮由显性基因控制,单眼皮由隐性基因控制.如果一对夫妻的遗传基因均为,其女士已怀孕,则小孩的眼睛为双眼皮的概率是 .
14.(2024·讷河期末)甲、乙两人参加社会实践活动,随机选取“做社区志愿者”和“做交通引导员”两项中的一项,两人同时选择“做社区志愿者”的概率是 .
15.(2021九上·宁德月考)小白有两张卡片,分别标有数字1,2;小黄有三张卡片,分别标有数字3,4,5.两人各自随机地取出一张卡片,取出的两张卡片上数字之积为奇数的概率是 .
16.在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( , ),其中点A,O,B不在同一直线上且-2≤ ≤2,-2≤ ≤2, , 均为整数,则所作OOAB为直角三角形的概率是 .
三、计算题
17.(2022九上·安源期中)课堂上,蒋老师拿出了4张分别与有数字1,2,3,4的卡片(除数字外其他都相同),让同学们随机抽取两张,并计算这两张卡片上数字的和.
(1)请用列表或画树状图的方法列举出所有等可能的结果;
(2)求两张卡片上数字的和大于5的概率.
18.(2024九上·上城月考)某高速收费站有三个通道(通道是指电子不停车收费的专用车道)A,B,C和一个人工收费通道D.
(1)求一辆办理过卡的汽车经过此收费站时,选择A通道通过的概率;
(2)现有都办理过卡的甲,乙两辆汽车都选择了通道通行,求甲,乙两辆车选择不同通道通过的概率.
四、解答题
19.(2024九上·锦江月考)嘉嘉所住小区的每栋楼下均设有供业主使用的公共停车场,这天他放学回家时观察到位于他家楼下的停车场还剩余四个车位,小区规定每辆汽车停放时只能占用一个车位.
(1)若此时有一辆汽车停车,则这辆车停在A车位的概率是___________;
(2)若此时有两辆汽车停车,用树状图或列表法求这两辆车停在相邻车位的概率.
20.(2024九上·武侯期末)甲、乙两人做游戏:每人都在纸上随机写一个到1之间的整数(包括和1).
(1)填空:甲写出非负整数的概率为______;
(2)将甲、乙两人所写整数相加,请用列表或画树状图的方法,求和的绝对值是1的概率.
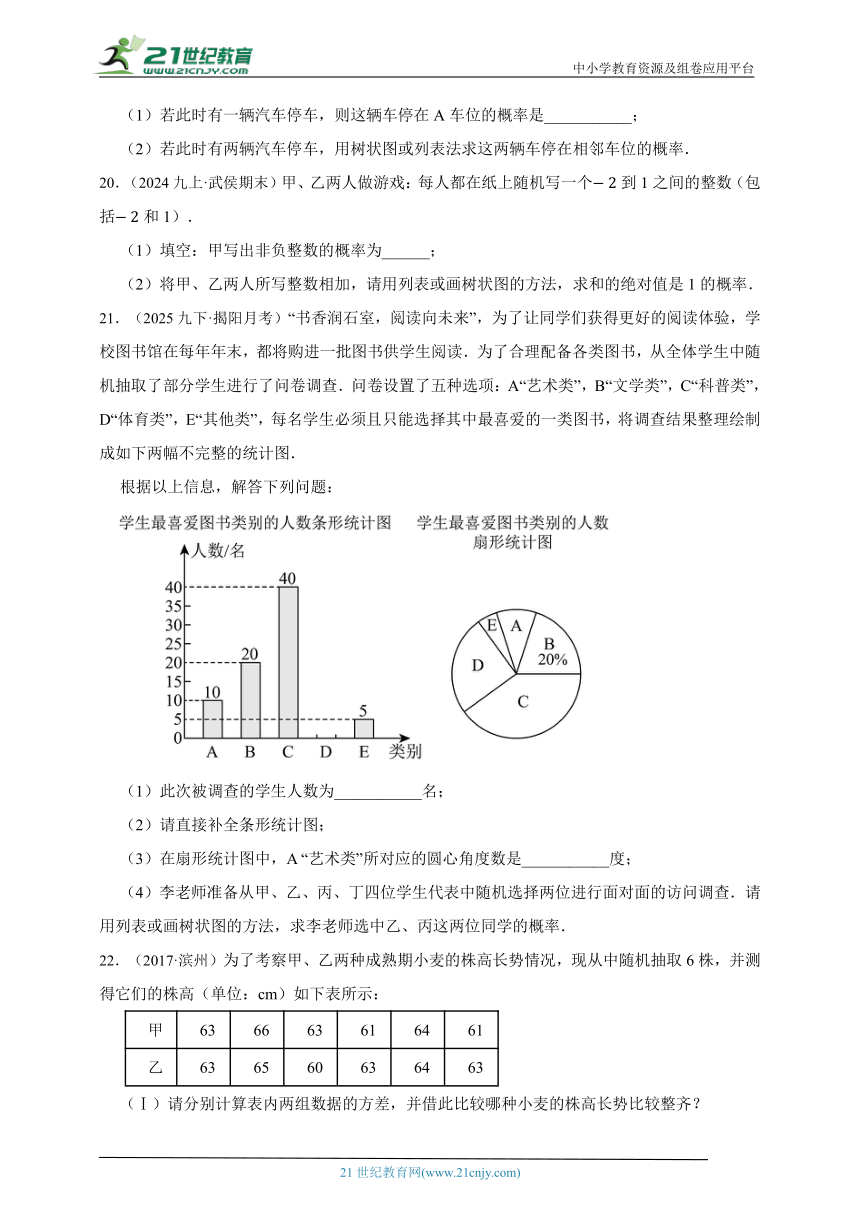
21.(2025九下·揭阳月考)“书香润石室,阅读向未来”,为了让同学们获得更好的阅读体验,学校图书馆在每年年末,都将购进一批图书供学生阅读.为了合理配备各类图书,从全体学生中随机抽取了部分学生进行了问卷调查.问卷设置了五种选项:A“艺术类”,B“文学类”,C“科普类”,D“体育类”,E“其他类”,每名学生必须且只能选择其中最喜爱的一类图书,将调查结果整理绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为___________名;
(2)请直接补全条形统计图;
(3)在扇形统计图中,A “艺术类”所对应的圆心角度数是___________度;
(4)李老师准备从甲、乙、丙、丁四位学生代表中随机选择两位进行面对面的访问调查.请用列表或画树状图的方法,求李老师选中乙、丙这两位同学的概率.
22.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
答案解析部分
1.【答案】A
【知识点】用列表法或树状图法求概率
2.【答案】B
【知识点】用列表法或树状图法求概率
3.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
4.【答案】B
【知识点】用列表法或树状图法求概率
5.【答案】C
【知识点】用列表法或树状图法求概率
6.【答案】D
【知识点】用列表法或树状图法求概率
7.【答案】D
【知识点】用列表法或树状图法求概率
8.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
9.【答案】B
【知识点】用列表法或树状图法求概率
10.【答案】D
【知识点】用列表法或树状图法求概率
11.【答案】
【知识点】用列表法或树状图法求概率;概率公式
12.【答案】
【知识点】用列表法或树状图法求概率
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】
【知识点】用列表法或树状图法求概率;概率公式
15.【答案】
【知识点】用列表法或树状图法求概率
16.【答案】
【知识点】用列表法或树状图法求概率
17.【答案】(1)共有12种等情况数;(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】(1),
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)100
(2)解:类的人数为:名,
补全条形统计图如下:
;
(3)36
(4)解:画树状图得:
∵共有12种等可能的结果,恰好同时选中乙、丙两位同学的有2种情况,
∴恰好同时选中乙、丙两位同学的概率为.
【知识点】扇形统计图;条形统计图;用列表法或树状图法求概率
22.【答案】解:(Ⅰ)∵ = =63,
∴s甲2= ×[(63﹣63)2×2+(66﹣63)2+2×(61﹣63)2+(64﹣63)2]=3;
∵ = =63,
∴s乙2= ×[(63﹣63)2×3+(65﹣63)2+(60﹣63)2+(64﹣63)2]= ,
∵s乙2<s甲2,
∴乙种小麦的株高长势比较整齐;
(Ⅱ)列表如下:
63 66 63 61 64 61
63 63、63 66、63 63、63 61、63 64、63 61、63
65 63、65 66、65 63、65 61、65 64、65 61、65
60 63、60 66、60 63、60 61、60 64、60 61、60
63 63、63 66、63 63、63 61、63 64、63 61、63
64 63、64 66、64 63、64 61、64 64、64 61、64
63 63、63 66、63 63、63 61、63 64、63 61、63
由表格可知,共有36种等可能结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,
∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为 = .
【知识点】用列表法或树状图法求概率;模拟实验;方差
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.列举所有机会均等的结果
一、单选题
1.(2025九上·莆田期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
2.(2023九上·和平期末)为了调动同学们学习数学的积极性,班内组织开展了数学素养大赛,老师将三道题的题号1,2,3,分别写在完全相同的3张卡片的正面,将卡片背面朝上洗匀.小李先从中随机抽取一张卡片,记录下卡片上的数字后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的数字,则两张卡片上的数字是“1”和“3”的概率为( )
A. B. C. D.
3.(2016·余姚模拟)有3个整式x,x+1,2,先随机取一个整式作为分子,再在余下的整式中随机取一个作为分母,恰能组成成分式的概率是( )
A. B. C. D.
4.(2024九上·贵阳月考)如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
A. B. C. D.
5.(2024九下·新县模拟)据中国载人航天工程办公室消息,北京时间年月日,神舟十六号、神舟十七号航天员乘组进行交接仪式,两个乘组移交了中国空间站的钥匙.空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设“神舟十七号”的三名航天员“汤洪波、唐胜杰、江新林”从核心舱进入问天实验舱和梦天实验舱开展实验的机会均等,现在要从这三名航天员中选人各进入一个实验舱开展科学实验,则汤洪波、唐胜杰两人同时被选中的概率为( )
A. B. C. D.
6.(2018九上·十堰期末)甲、乙、丙三人参加数学、物理、英语三项竞赛,每人限报一项,每项限报一人,则甲报英语、乙报数学、丙报物理的概率是( )
A. B. C. D.
7.(2017·河南模拟)用m,n,p,q四把钥匙去开A,B两把锁,其中仅有钥匙m能打开锁A,仅有钥匙n能打开锁B,则“取一把钥匙恰能打开一把锁”的概率是( )
A. B. C. D.
8.(2023九上·青秀期末)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界普为“中国第五大发明”,小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( )
A. B. C. D.
9.(2020九上·大石桥月考)小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
A. B. C. D.
10.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( )
A. B. C. D.
二、填空题
11.(2025·曾都模拟)为发展学生的阅读素养,某校开设了《西游记》,《三国演义》,《水浒传》和《红楼梦》四个整本书阅读项目,小红随机抽取两个项目进行阅读,恰好抽到《西游记》和《红楼梦》阅读项目的概率是 .
12.(2020·南漳模拟)在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1,﹣2,3,4,随机摸取一个小球记下标号后放回,再随机摸取一个小球记下标号,则两次摸取的小球的标号之积为负数的概率为 .
13.(2023·巴中模拟)生物体的性状通常是由一对基因控制的,当控制某种性状的一对基因都是显性或一个是显性、一个是隐性时,生物体表现出显性基因控制的性状;当控制某种性状的基因都是隐性时,隐性基因控制的性状才会表现出来.在单、双眼皮的性状遗传中,双眼皮由显性基因控制,单眼皮由隐性基因控制.如果一对夫妻的遗传基因均为,其女士已怀孕,则小孩的眼睛为双眼皮的概率是 .
14.(2024·讷河期末)甲、乙两人参加社会实践活动,随机选取“做社区志愿者”和“做交通引导员”两项中的一项,两人同时选择“做社区志愿者”的概率是 .
15.(2021九上·宁德月考)小白有两张卡片,分别标有数字1,2;小黄有三张卡片,分别标有数字3,4,5.两人各自随机地取出一张卡片,取出的两张卡片上数字之积为奇数的概率是 .
16.在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( , ),其中点A,O,B不在同一直线上且-2≤ ≤2,-2≤ ≤2, , 均为整数,则所作OOAB为直角三角形的概率是 .
三、计算题
17.(2022九上·安源期中)课堂上,蒋老师拿出了4张分别与有数字1,2,3,4的卡片(除数字外其他都相同),让同学们随机抽取两张,并计算这两张卡片上数字的和.
(1)请用列表或画树状图的方法列举出所有等可能的结果;
(2)求两张卡片上数字的和大于5的概率.
18.(2024九上·上城月考)某高速收费站有三个通道(通道是指电子不停车收费的专用车道)A,B,C和一个人工收费通道D.
(1)求一辆办理过卡的汽车经过此收费站时,选择A通道通过的概率;
(2)现有都办理过卡的甲,乙两辆汽车都选择了通道通行,求甲,乙两辆车选择不同通道通过的概率.
四、解答题
19.(2024九上·锦江月考)嘉嘉所住小区的每栋楼下均设有供业主使用的公共停车场,这天他放学回家时观察到位于他家楼下的停车场还剩余四个车位,小区规定每辆汽车停放时只能占用一个车位.
(1)若此时有一辆汽车停车,则这辆车停在A车位的概率是___________;
(2)若此时有两辆汽车停车,用树状图或列表法求这两辆车停在相邻车位的概率.
20.(2024九上·武侯期末)甲、乙两人做游戏:每人都在纸上随机写一个到1之间的整数(包括和1).
(1)填空:甲写出非负整数的概率为______;
(2)将甲、乙两人所写整数相加,请用列表或画树状图的方法,求和的绝对值是1的概率.
21.(2025九下·揭阳月考)“书香润石室,阅读向未来”,为了让同学们获得更好的阅读体验,学校图书馆在每年年末,都将购进一批图书供学生阅读.为了合理配备各类图书,从全体学生中随机抽取了部分学生进行了问卷调查.问卷设置了五种选项:A“艺术类”,B“文学类”,C“科普类”,D“体育类”,E“其他类”,每名学生必须且只能选择其中最喜爱的一类图书,将调查结果整理绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为___________名;
(2)请直接补全条形统计图;
(3)在扇形统计图中,A “艺术类”所对应的圆心角度数是___________度;
(4)李老师准备从甲、乙、丙、丁四位学生代表中随机选择两位进行面对面的访问调查.请用列表或画树状图的方法,求李老师选中乙、丙这两位同学的概率.
22.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
答案解析部分
1.【答案】A
【知识点】用列表法或树状图法求概率
2.【答案】B
【知识点】用列表法或树状图法求概率
3.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
4.【答案】B
【知识点】用列表法或树状图法求概率
5.【答案】C
【知识点】用列表法或树状图法求概率
6.【答案】D
【知识点】用列表法或树状图法求概率
7.【答案】D
【知识点】用列表法或树状图法求概率
8.【答案】C
【知识点】用列表法或树状图法求概率;概率公式
9.【答案】B
【知识点】用列表法或树状图法求概率
10.【答案】D
【知识点】用列表法或树状图法求概率
11.【答案】
【知识点】用列表法或树状图法求概率;概率公式
12.【答案】
【知识点】用列表法或树状图法求概率
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】
【知识点】用列表法或树状图法求概率;概率公式
15.【答案】
【知识点】用列表法或树状图法求概率
16.【答案】
【知识点】用列表法或树状图法求概率
17.【答案】(1)共有12种等情况数;(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】(1),
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)100
(2)解:类的人数为:名,
补全条形统计图如下:
;
(3)36
(4)解:画树状图得:
∵共有12种等可能的结果,恰好同时选中乙、丙两位同学的有2种情况,
∴恰好同时选中乙、丙两位同学的概率为.
【知识点】扇形统计图;条形统计图;用列表法或树状图法求概率
22.【答案】解:(Ⅰ)∵ = =63,
∴s甲2= ×[(63﹣63)2×2+(66﹣63)2+2×(61﹣63)2+(64﹣63)2]=3;
∵ = =63,
∴s乙2= ×[(63﹣63)2×3+(65﹣63)2+(60﹣63)2+(64﹣63)2]= ,
∵s乙2<s甲2,
∴乙种小麦的株高长势比较整齐;
(Ⅱ)列表如下:
63 66 63 61 64 61
63 63、63 66、63 63、63 61、63 64、63 61、63
65 63、65 66、65 63、65 61、65 64、65 61、65
60 63、60 66、60 63、60 61、60 64、60 61、60
63 63、63 66、63 63、63 61、63 64、63 61、63
64 63、64 66、64 63、64 61、64 64、64 61、64
63 63、63 66、63 63、63 61、63 64、63 61、63
由表格可知,共有36种等可能结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,
∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为 = .
【知识点】用列表法或树状图法求概率;模拟实验;方差
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
