第23章 图形的相似检测题(含答案)
文档属性
| 名称 | 第23章 图形的相似检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:17:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第23章 图形的相似检测题
一、单选题
1.(2024七下·银川期末)下列各组数中能构成一个三角形边长的是( )
A.5,5,11 B.6,8,10 C.8,7,15 D.10,20,30
2.(2024八上·富源期中)以下列各组线段为边,不能组成三角形的是( )
A.2,3,4 B.3,3,5 C.1,3,5 D.5,6,3
3.(2019九上·沙坪坝月考)如图,在 中, .若 , ,则下列结论中正确的是( )
A. B. C. D.
4.(2017九上·双城开学考)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B.4 C.3 D.3
5.(2019八上·重庆月考)下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( ).
A.13,12,20 B.8,7,15 C.3,4,8 D.5,5,11
6.如图,矩形ABCD中,,,动点E,F分别从点A,C同时出发,以每秒1个单位长度的速度沿AB,CD向终点B,D运动,过点E,F作直线l,过点A作直线l的垂线,垂足为G,则AG的最大值为( )
A. B. C.2 D.1
7.(2024八上·花溪期中)如果一个三角形的两边长分别为、,那么这个三角形的第三边的长可以是( )
A. B. C. D.
8.(2024九上·六盘水月考)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
9.(2022·惠山模拟)如图,在△ABC中,∠BAC=30°,AC=4,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转30°得到CF,连接AF,则△AFC的面积变化情况是( )
A.先变大再变小 B.先变小再变大
C.逐渐变大 D.不变
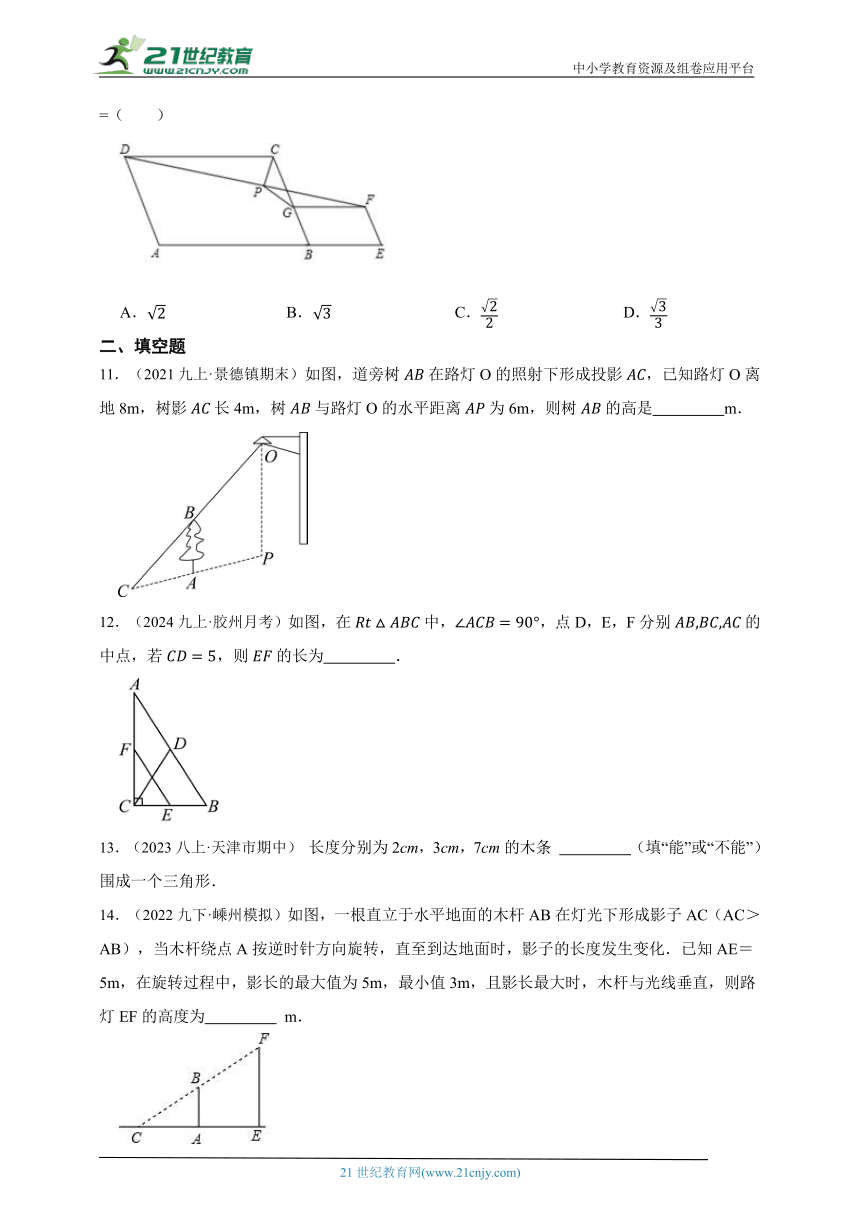
10.(2020九下·碑林月考)如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A, B, E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则 =( )
A. B. C. D.
二、填空题
11.(2021九上·景德镇期末)如图,道旁树在路灯O的照射下形成投影,已知路灯O离地8m,树影长4m,树与路灯O的水平距离为6m,则树的高是 m.
12.(2024九上·胶州月考)如图,在中,,点D,E,F分别的中点,若,则的长为 .
13.(2023八上·天津市期中) 长度分别为2cm,3cm,7cm的木条 (填“能”或“不能”)围成一个三角形.
14.(2022九下·嵊州模拟)如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
15.(2024九下·东湖开学考)如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为 .
16.(2024九下·西安期中)如图,在中,,,,D、F分别是边、上的动点,连接,过点A作交于点E,垂足为G,连接,则的最小值为 .
三、计算题
17.(2022九下·定州模拟)先化简,再求值:÷,其中tan45°.
18.(2022九上·长安期末)计算:
19.(2024九上·双流期末)如图,在平面直角坐标系中,直线与反比例函数的图象交于,B两点,C为反比例函数图象第四象限上一动点.
(1)求反比例函数的表达式及点B的坐标;
(2)当四边形的面积为36时,求此时点C的坐标;
(3)我们把对角线互相垂直且相等的四边形称为“垂等四边形”.设点D是平面内一点,是否存在这样的C,D两点,使四边形是“垂等四边形”,且?若存在,求出C,D两点的坐标;若不存在,请说明理由.
四、解答题
20.(2025·东阳模拟)如图,在菱形中,作,连结.
(1)求菱形的面积;
(2)求的长.
21.(2024九上·南京期末)如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中为下水管道口直径,为可绕转轴自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径,为检修时阀门开启的位置,且.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达位置时,在点处测得俯角,若此时点恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
22.如图,葡萄园大棚支架的顶部形如等腰三角形ABC.经测量,钢条AD⊥BC,BC=600cm,∠B=38°.(精确到1cm,参考数据:sin38°≈0.616,cos38°≈0.788,tan38°≈0.781).
(1)求钢条AB的长.
(2)为了加固支架,现在顶部加两根钢条DE和DF,已知DE⊥AB于点E,DF⊥AC于点F,求DE的长.
23.(2023·桥西模拟)如图,矩形纸片,点在边上(点不与点重合),折叠该纸片,使折痕所在的直线经过点,并与射线交于点,且,点的对应点为,设.
(1)如图①,当点落在上时,求的大小及的值;
(2)如图②,若折叠后重合部分为四边形,分别与边相交于点,试用含有的式子表示的长,并直接写出的取值范围;
(3)随着的变化,折叠后重合部分的面积能否在某个值段保持不变,若能,直接写出这个值段的长;若不能,请说明理由.
答案解析部分
1.【答案】B
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形三边关系
3.【答案】C
【知识点】锐角三角函数的定义
4.【答案】A
【知识点】等腰三角形的性质;含30°角的直角三角形;旋转的性质
5.【答案】A
【知识点】三角形三边关系
6.【答案】D
【知识点】勾股定理;矩形的性质;直角三角形斜边上的中线
7.【答案】C
【知识点】三角形三边关系
8.【答案】C
【知识点】含30°角的直角三角形;勾股定理;正方形的性质
9.【答案】D
【知识点】三角形的面积;含30°角的直角三角形;旋转的性质;三角形全等的判定-SAS
10.【答案】B
【知识点】全等三角形的判定与性质;等腰三角形的判定与性质;菱形的判定与性质;锐角三角函数的定义;求特殊角的三角函数值
11.【答案】3.2
【知识点】相似三角形的实际应用
12.【答案】5
【知识点】三角形的中位线定理;直角三角形斜边上的中线
13.【答案】不能
【知识点】三角形三边关系
14.【答案】7.5
【知识点】相似三角形的实际应用
15.【答案】
【知识点】等腰三角形的性质;解直角三角形
16.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质;解直角三角形
17.【答案】,
【知识点】分式的化简求值;分母有理化;求特殊角的三角函数值
18.【答案】解:原式=
=
=
【知识点】二次根式的混合运算;求特殊角的三角函数值
19.【答案】(1),
(2)或
(3)
【知识点】反比例函数与一次函数的交点问题;等腰三角形的判定与性质;勾股定理;解直角三角形
20.【答案】(1)80
(2)
【知识点】勾股定理;菱形的性质;解直角三角形
21.【答案】(1);(2)
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】(1)解:在等腰三角形ABC中,AD⊥BC,
∴BC=2BD=600cm,
∴BD=300cm.
∵∠B=38°,
∴AB==≈381(cm),
∴AB的长约为381cm
(2)解:∵DE⊥AB,
∴DE=BD·sinB=300×0.616≈185(cm),
∴DE的长为185cm
【知识点】等腰三角形的性质;解直角三角形的其他实际应用
23.【答案】(1),
(2)
(3)能,
【知识点】含30°角的直角三角形;矩形的性质;翻折变换(折叠问题);解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第23章 图形的相似检测题
一、单选题
1.(2024七下·银川期末)下列各组数中能构成一个三角形边长的是( )
A.5,5,11 B.6,8,10 C.8,7,15 D.10,20,30
2.(2024八上·富源期中)以下列各组线段为边,不能组成三角形的是( )
A.2,3,4 B.3,3,5 C.1,3,5 D.5,6,3
3.(2019九上·沙坪坝月考)如图,在 中, .若 , ,则下列结论中正确的是( )
A. B. C. D.
4.(2017九上·双城开学考)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B.4 C.3 D.3
5.(2019八上·重庆月考)下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( ).
A.13,12,20 B.8,7,15 C.3,4,8 D.5,5,11
6.如图,矩形ABCD中,,,动点E,F分别从点A,C同时出发,以每秒1个单位长度的速度沿AB,CD向终点B,D运动,过点E,F作直线l,过点A作直线l的垂线,垂足为G,则AG的最大值为( )
A. B. C.2 D.1
7.(2024八上·花溪期中)如果一个三角形的两边长分别为、,那么这个三角形的第三边的长可以是( )
A. B. C. D.
8.(2024九上·六盘水月考)如图,在边长为3的正方形中,,,则的长是( )
A.1 B. C. D.2
9.(2022·惠山模拟)如图,在△ABC中,∠BAC=30°,AC=4,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转30°得到CF,连接AF,则△AFC的面积变化情况是( )
A.先变大再变小 B.先变小再变大
C.逐渐变大 D.不变
10.(2020九下·碑林月考)如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A, B, E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则 =( )
A. B. C. D.
二、填空题
11.(2021九上·景德镇期末)如图,道旁树在路灯O的照射下形成投影,已知路灯O离地8m,树影长4m,树与路灯O的水平距离为6m,则树的高是 m.
12.(2024九上·胶州月考)如图,在中,,点D,E,F分别的中点,若,则的长为 .
13.(2023八上·天津市期中) 长度分别为2cm,3cm,7cm的木条 (填“能”或“不能”)围成一个三角形.
14.(2022九下·嵊州模拟)如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
15.(2024九下·东湖开学考)如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为 .
16.(2024九下·西安期中)如图,在中,,,,D、F分别是边、上的动点,连接,过点A作交于点E,垂足为G,连接,则的最小值为 .
三、计算题
17.(2022九下·定州模拟)先化简,再求值:÷,其中tan45°.
18.(2022九上·长安期末)计算:
19.(2024九上·双流期末)如图,在平面直角坐标系中,直线与反比例函数的图象交于,B两点,C为反比例函数图象第四象限上一动点.
(1)求反比例函数的表达式及点B的坐标;
(2)当四边形的面积为36时,求此时点C的坐标;
(3)我们把对角线互相垂直且相等的四边形称为“垂等四边形”.设点D是平面内一点,是否存在这样的C,D两点,使四边形是“垂等四边形”,且?若存在,求出C,D两点的坐标;若不存在,请说明理由.
四、解答题
20.(2025·东阳模拟)如图,在菱形中,作,连结.
(1)求菱形的面积;
(2)求的长.
21.(2024九上·南京期末)如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中为下水管道口直径,为可绕转轴自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径,为检修时阀门开启的位置,且.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达位置时,在点处测得俯角,若此时点恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
22.如图,葡萄园大棚支架的顶部形如等腰三角形ABC.经测量,钢条AD⊥BC,BC=600cm,∠B=38°.(精确到1cm,参考数据:sin38°≈0.616,cos38°≈0.788,tan38°≈0.781).
(1)求钢条AB的长.
(2)为了加固支架,现在顶部加两根钢条DE和DF,已知DE⊥AB于点E,DF⊥AC于点F,求DE的长.
23.(2023·桥西模拟)如图,矩形纸片,点在边上(点不与点重合),折叠该纸片,使折痕所在的直线经过点,并与射线交于点,且,点的对应点为,设.
(1)如图①,当点落在上时,求的大小及的值;
(2)如图②,若折叠后重合部分为四边形,分别与边相交于点,试用含有的式子表示的长,并直接写出的取值范围;
(3)随着的变化,折叠后重合部分的面积能否在某个值段保持不变,若能,直接写出这个值段的长;若不能,请说明理由.
答案解析部分
1.【答案】B
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形三边关系
3.【答案】C
【知识点】锐角三角函数的定义
4.【答案】A
【知识点】等腰三角形的性质;含30°角的直角三角形;旋转的性质
5.【答案】A
【知识点】三角形三边关系
6.【答案】D
【知识点】勾股定理;矩形的性质;直角三角形斜边上的中线
7.【答案】C
【知识点】三角形三边关系
8.【答案】C
【知识点】含30°角的直角三角形;勾股定理;正方形的性质
9.【答案】D
【知识点】三角形的面积;含30°角的直角三角形;旋转的性质;三角形全等的判定-SAS
10.【答案】B
【知识点】全等三角形的判定与性质;等腰三角形的判定与性质;菱形的判定与性质;锐角三角函数的定义;求特殊角的三角函数值
11.【答案】3.2
【知识点】相似三角形的实际应用
12.【答案】5
【知识点】三角形的中位线定理;直角三角形斜边上的中线
13.【答案】不能
【知识点】三角形三边关系
14.【答案】7.5
【知识点】相似三角形的实际应用
15.【答案】
【知识点】等腰三角形的性质;解直角三角形
16.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质;解直角三角形
17.【答案】,
【知识点】分式的化简求值;分母有理化;求特殊角的三角函数值
18.【答案】解:原式=
=
=
【知识点】二次根式的混合运算;求特殊角的三角函数值
19.【答案】(1),
(2)或
(3)
【知识点】反比例函数与一次函数的交点问题;等腰三角形的判定与性质;勾股定理;解直角三角形
20.【答案】(1)80
(2)
【知识点】勾股定理;菱形的性质;解直角三角形
21.【答案】(1);(2)
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】(1)解:在等腰三角形ABC中,AD⊥BC,
∴BC=2BD=600cm,
∴BD=300cm.
∵∠B=38°,
∴AB==≈381(cm),
∴AB的长约为381cm
(2)解:∵DE⊥AB,
∴DE=BD·sinB=300×0.616≈185(cm),
∴DE的长为185cm
【知识点】等腰三角形的性质;解直角三角形的其他实际应用
23.【答案】(1),
(2)
(3)能,
【知识点】含30°角的直角三角形;矩形的性质;翻折变换(折叠问题);解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
