第24章 解直角三角形检测题(含答案)
文档属性
| 名称 | 第24章 解直角三角形检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 467.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:17:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第24章 解直角三角形检测题
一、单选题
1.如图,为估计池塘岸边A、B的距离,甲、乙二人在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离可能是( )
A.5米 B.15米 C.25米 D.30米
2.(2024八上·桑植期中)下列长度的三条线段能组成三角形的是( )
A. B. C. D.
3.(2024九上·城阳月考)已知三角形的两边分别是3和5,第三边是方程的根,则这个三角形的周长为( )
A. B.或 C. D.9
4.(2024七下·光明期中)如图,为估计池塘两岸,间的距离,小明在池塘一侧选取了一点,测得,,那么间的距离不可能是( )
A. B. C. D.
5.(2025·新会模拟)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16
6.(2022九上·济南期末)如图,我市在建高铁的某段路基横断面为梯形,.长6米,坡度为,的坡度为,则长为( ) 米
A. B. C. D.
7.(2021九上·宜宾期末)将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )
A. B. C. D.
8.(2019八上·齐齐哈尔期中)已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么( )
A.M>0 B.M=0 C.M<0 D.不能确定
9.(2019九上·长春期末)如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
10.(2023八下·鹤城期末)如图,点B在x轴上,,将绕点O按顺时针方向旋转,每次旋转,则第2023次旋转结束后,点B所在位置的坐标是( )
A. B. C. D.
二、填空题
11.(2019八下·城区期末)已知三角形两边长分别为2,3,那么第三边的长可以是 .
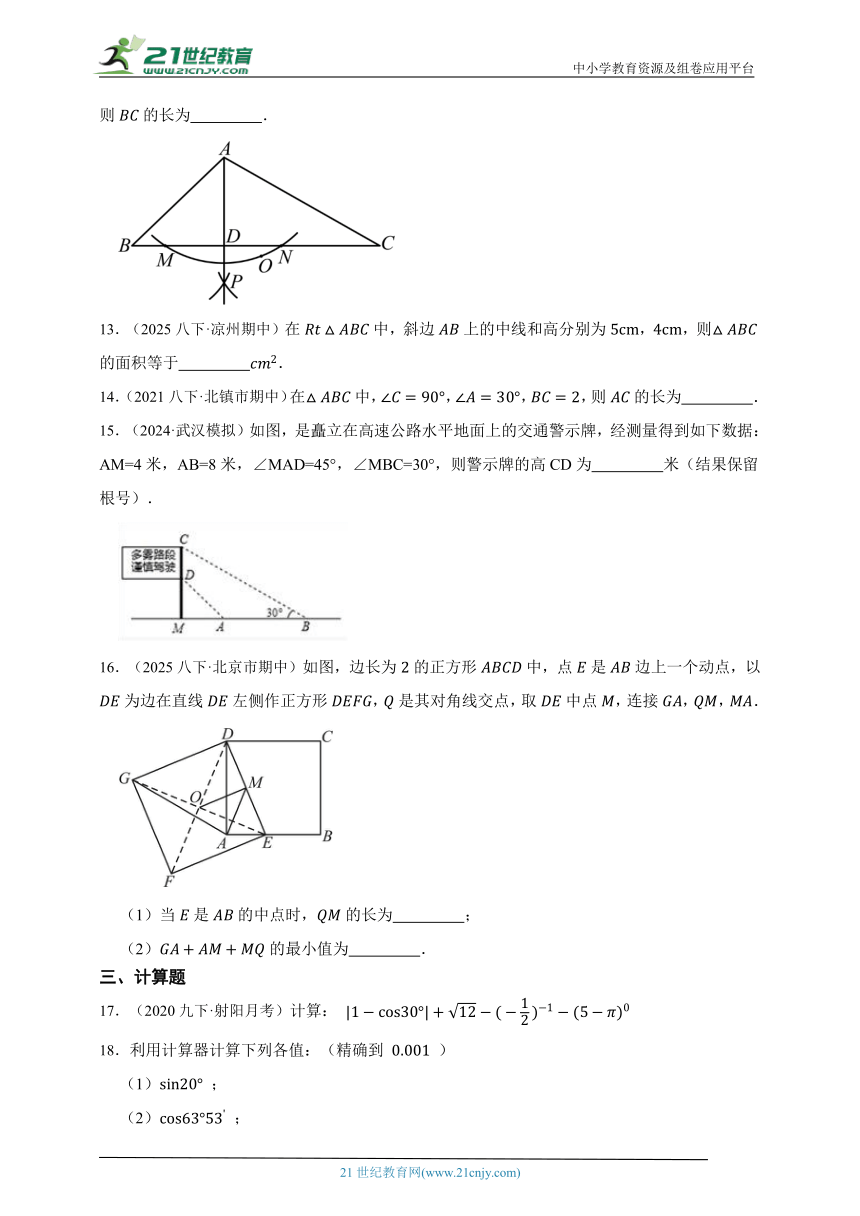
12.(2024九下·吉林模拟)如图,在中,,任取一点,使点和点在直线的两侧,以点为圆心,长为半径作弧,交于点,,分别以点,为圆心,大于长为半径作弧,两弧相交于点,作射线,交于点.若的长为,则的长为 .
13.(2025八下·凉州期中)在中,斜边上的中线和高分别为,,则的面积等于 .
14.(2021八下·北镇市期中)在中,,,,则的长为 .
15.(2024·武汉模拟)如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果保留根号).
16.(2025八下·北京市期中)如图,边长为的正方形中,点是边上一个动点,以为边在直线左侧作正方形,是其对角线交点,取中点,连接,,.
(1)当是的中点时,的长为 ;
(2)的最小值为 .
三、计算题
17.(2020九下·射阳月考)计算:
18.利用计算器计算下列各值:(精确到 )
(1) ;
(2) ;
(3)
19.(2024八上·昭阳月考)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
四、解答题
20.(2024九上·江北期中)如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
21.(2023九下·中山期中)如图,某公园入口处原有三级台阶,每级台阶高为,宽为,为方便残疾人通行,现将台阶改为斜坡,设台阶的起点为,斜坡的起始点为,现设计斜坡的坡度为.求的长度.
22.(2023九上·栾城期中) 如图,某天然气公司的主输气管道途经A小区,继续沿A小区的北偏东60°方向往前铺设.测绘员在A处测得另一个需要安装天然气的P小区位于北偏东30°方向,测绘员从A处出发,沿主输气管道方向前行2000米
到达B处,此时测得P小区位于北偏西75°方向.
(1) 度, 度;
(2)现要在主输气管道AB上选择一个支管道连接点Q,使从Q处到P小区铺设的管道最短,求A小区与支管道连接点Q的距离.(结果保留根号)
23.(2023九上·上海市月考)已知:如图,在矩形中,是对角线上一点(与不重合),平分交边于点,交于点.
(1)当时,求的长;
(2)当与相似时,求的正切值;
(3)如果的面积是面积的2倍,求的长.
答案解析部分
1.【答案】B
【知识点】三角形三边关系
2.【答案】D
【知识点】三角形三边关系
3.【答案】C
【知识点】因式分解法解一元二次方程;三角形三边关系
4.【答案】A
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形三边关系
6.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
7.【答案】D
【知识点】矩形的性质;翻折变换(折叠问题);互余两角三角函数的关系
8.【答案】C
【知识点】三角形三边关系
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】A
【知识点】含30°角的直角三角形;坐标与图形变化﹣旋转
11.【答案】2(答案不唯一)
【知识点】三角形三边关系
12.【答案】
【知识点】等腰三角形的判定与性质;解直角三角形;尺规作图-垂直平分线
13.【答案】20
【知识点】直角三角形斜边上的中线
14.【答案】
【知识点】含30°角的直角三角形;勾股定理
15.【答案】 一4
【知识点】解直角三角形的其他实际应用
16.【答案】;
【知识点】勾股定理;正方形的性质;轴对称的性质;直角三角形斜边上的中线
17.【答案】解:原式
【知识点】实数的运算;零指数幂;负整数指数幂;求特殊角的三角函数值
18.【答案】(1)解: ≈0.342
(2)解: ≈0.496
(3)解: ≈0.999
【知识点】计算器—三角函数;近似数及有效数字
19.【答案】(1)的周长为
(2)
【知识点】三角形三边关系;化简含绝对值有理数
20.【答案】300米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】的长度为.
【知识点】解直角三角形的实际应用﹣坡度坡角问题
22.【答案】(1)30;45
(2)解:如下图所示,过点P作于Q,
则此时从Q处到P小区铺设的管道最短,设米.
∵,
∴米,米.
∴米.
∵米,
∴.
∴.
∴米.
答:A小区与支管道连接点Q的距离是米.
【知识点】角的运算;垂线段最短及其应用;解直角三角形的实际应用﹣方向角问题
23.【答案】(1)3
(2)或1
(3)
【知识点】三角形全等及其性质;矩形的性质;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第24章 解直角三角形检测题
一、单选题
1.如图,为估计池塘岸边A、B的距离,甲、乙二人在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离可能是( )
A.5米 B.15米 C.25米 D.30米
2.(2024八上·桑植期中)下列长度的三条线段能组成三角形的是( )
A. B. C. D.
3.(2024九上·城阳月考)已知三角形的两边分别是3和5,第三边是方程的根,则这个三角形的周长为( )
A. B.或 C. D.9
4.(2024七下·光明期中)如图,为估计池塘两岸,间的距离,小明在池塘一侧选取了一点,测得,,那么间的距离不可能是( )
A. B. C. D.
5.(2025·新会模拟)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16
6.(2022九上·济南期末)如图,我市在建高铁的某段路基横断面为梯形,.长6米,坡度为,的坡度为,则长为( ) 米
A. B. C. D.
7.(2021九上·宜宾期末)将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )
A. B. C. D.
8.(2019八上·齐齐哈尔期中)已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么( )
A.M>0 B.M=0 C.M<0 D.不能确定
9.(2019九上·长春期末)如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A. B. C. D.
10.(2023八下·鹤城期末)如图,点B在x轴上,,将绕点O按顺时针方向旋转,每次旋转,则第2023次旋转结束后,点B所在位置的坐标是( )
A. B. C. D.
二、填空题
11.(2019八下·城区期末)已知三角形两边长分别为2,3,那么第三边的长可以是 .
12.(2024九下·吉林模拟)如图,在中,,任取一点,使点和点在直线的两侧,以点为圆心,长为半径作弧,交于点,,分别以点,为圆心,大于长为半径作弧,两弧相交于点,作射线,交于点.若的长为,则的长为 .
13.(2025八下·凉州期中)在中,斜边上的中线和高分别为,,则的面积等于 .
14.(2021八下·北镇市期中)在中,,,,则的长为 .
15.(2024·武汉模拟)如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 米(结果保留根号).
16.(2025八下·北京市期中)如图,边长为的正方形中,点是边上一个动点,以为边在直线左侧作正方形,是其对角线交点,取中点,连接,,.
(1)当是的中点时,的长为 ;
(2)的最小值为 .
三、计算题
17.(2020九下·射阳月考)计算:
18.利用计算器计算下列各值:(精确到 )
(1) ;
(2) ;
(3)
19.(2024八上·昭阳月考)按要求完成下列各小题.
(1)在中,,,的长为偶数,求的周长;
(2)已知的三边长分别为3,5,a,化简.
四、解答题
20.(2024九上·江北期中)如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
21.(2023九下·中山期中)如图,某公园入口处原有三级台阶,每级台阶高为,宽为,为方便残疾人通行,现将台阶改为斜坡,设台阶的起点为,斜坡的起始点为,现设计斜坡的坡度为.求的长度.
22.(2023九上·栾城期中) 如图,某天然气公司的主输气管道途经A小区,继续沿A小区的北偏东60°方向往前铺设.测绘员在A处测得另一个需要安装天然气的P小区位于北偏东30°方向,测绘员从A处出发,沿主输气管道方向前行2000米
到达B处,此时测得P小区位于北偏西75°方向.
(1) 度, 度;
(2)现要在主输气管道AB上选择一个支管道连接点Q,使从Q处到P小区铺设的管道最短,求A小区与支管道连接点Q的距离.(结果保留根号)
23.(2023九上·上海市月考)已知:如图,在矩形中,是对角线上一点(与不重合),平分交边于点,交于点.
(1)当时,求的长;
(2)当与相似时,求的正切值;
(3)如果的面积是面积的2倍,求的长.
答案解析部分
1.【答案】B
【知识点】三角形三边关系
2.【答案】D
【知识点】三角形三边关系
3.【答案】C
【知识点】因式分解法解一元二次方程;三角形三边关系
4.【答案】A
【知识点】三角形三边关系
5.【答案】C
【知识点】三角形三边关系
6.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
7.【答案】D
【知识点】矩形的性质;翻折变换(折叠问题);互余两角三角函数的关系
8.【答案】C
【知识点】三角形三边关系
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】A
【知识点】含30°角的直角三角形;坐标与图形变化﹣旋转
11.【答案】2(答案不唯一)
【知识点】三角形三边关系
12.【答案】
【知识点】等腰三角形的判定与性质;解直角三角形;尺规作图-垂直平分线
13.【答案】20
【知识点】直角三角形斜边上的中线
14.【答案】
【知识点】含30°角的直角三角形;勾股定理
15.【答案】 一4
【知识点】解直角三角形的其他实际应用
16.【答案】;
【知识点】勾股定理;正方形的性质;轴对称的性质;直角三角形斜边上的中线
17.【答案】解:原式
【知识点】实数的运算;零指数幂;负整数指数幂;求特殊角的三角函数值
18.【答案】(1)解: ≈0.342
(2)解: ≈0.496
(3)解: ≈0.999
【知识点】计算器—三角函数;近似数及有效数字
19.【答案】(1)的周长为
(2)
【知识点】三角形三边关系;化简含绝对值有理数
20.【答案】300米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】的长度为.
【知识点】解直角三角形的实际应用﹣坡度坡角问题
22.【答案】(1)30;45
(2)解:如下图所示,过点P作于Q,
则此时从Q处到P小区铺设的管道最短,设米.
∵,
∴米,米.
∴米.
∵米,
∴.
∴.
∴米.
答:A小区与支管道连接点Q的距离是米.
【知识点】角的运算;垂线段最短及其应用;解直角三角形的实际应用﹣方向角问题
23.【答案】(1)3
(2)或1
(3)
【知识点】三角形全等及其性质;矩形的性质;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
