23.1 成比例线段本节综合题 同步练习(含答案)
文档属性
| 名称 | 23.1 成比例线段本节综合题 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 481.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:50:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
23.1 成比例线段本届综合题
一、单选题
1.(2024九上·通州期中)鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工,如图,P是的黄金分割点(),那么( )
A. B. C. D.
2.(2025九上·赣榆期末)王老师的电脑显示器分辨率为,当她全屏浏览尺寸为(“”表示像素)的图片时,由于不成比例(),画面两边会出现黑色区域,若成比例就不会出现此问题,王老师全屏浏览以下四种尺寸的图片时,画面四周都不会出现黑边的是( )
A. B.
C. D.
3.(2024九上·西湖月考)如图,直线,分别交直线,于点,,,,,.若,,则的长为( )
A.4 B.5 C.6 D.10
4.(2024八下·苏州工业园月考)如图,在中,,若,,则的长为( )
A.4 B.6 C.8 D.10
5.(2025九上·路桥期末)如图,,若,,则的长为( )
A.6 B.9 C.12 D.15
6.(2022九上·江干月考)如图,已知线段AB=2,点P是线段AB的黄金分割点(APA. B. C. D.
7.(2020九上·亳州期中)AD 是△ABC 的中线,E 是 AD 上一点,AE= AD,BE 的延长线交 AC 于 F,则 的值为( )
A. B. C. D.
8.(2020九上·马鞍山期末)若点 为线段 的黄金分割点,且 ,则下列各式中错误的是( )
A. B.
C. D.
9.(2023九上·萧山期中)一本书的宽与长之比为黄金比,书的宽为14cm,则它的长为( )cm.
A.7+7 B.21-7 C.7-7 D.7-21
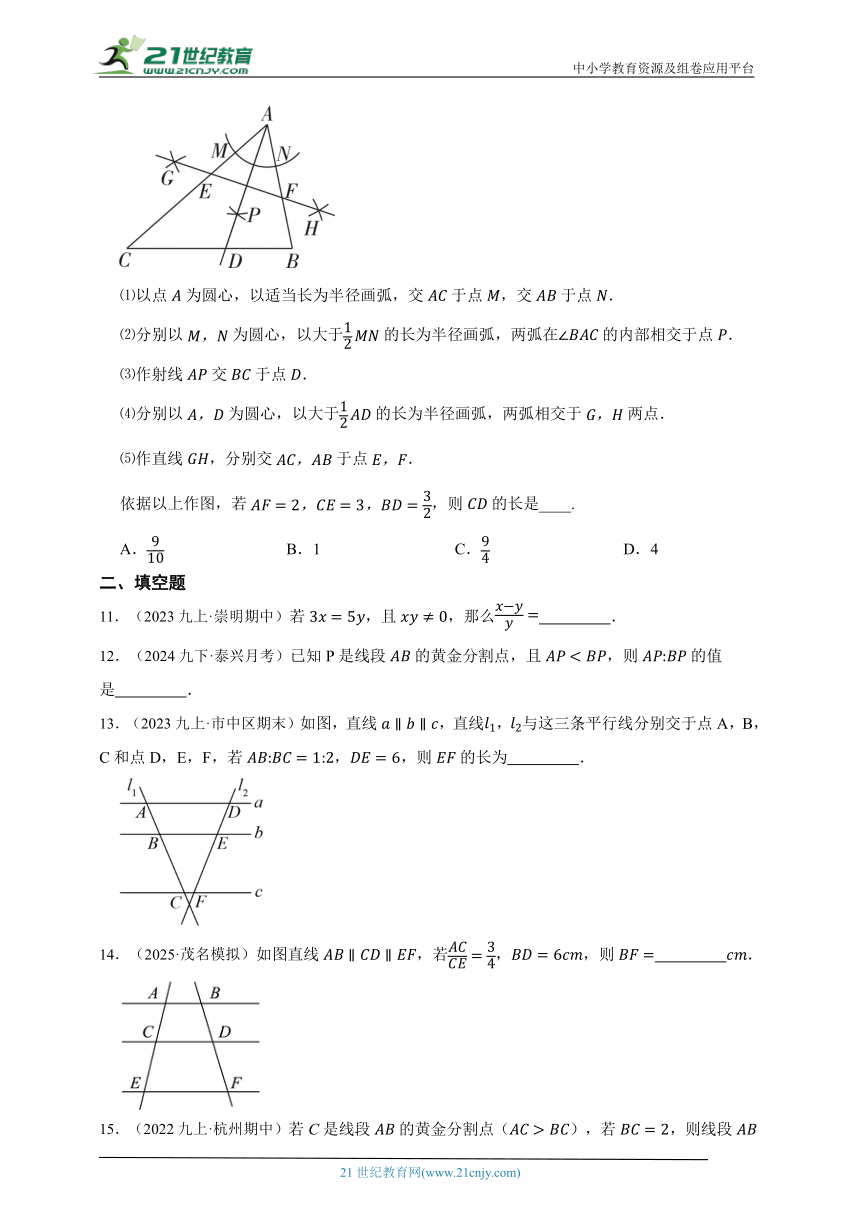
10.如图,已知.
⑴以点为圆心,以适当长为半径画弧,交于点,交于点.
⑵分别以为圆心,以大于的长为半径画弧,两弧在的内部相交于点.
⑶作射线交于点.
⑷分别以为圆心,以大于的长为半径画弧,两弧相交于两点.
⑸作直线,分别交于点.
依据以上作图,若,则的长是____.
A. B.1 C. D.4
二、填空题
11.(2023九上·崇明期中)若,且,那么 .
12.(2024九下·泰兴月考)已知P是线段的黄金分割点,且,则的值是 .
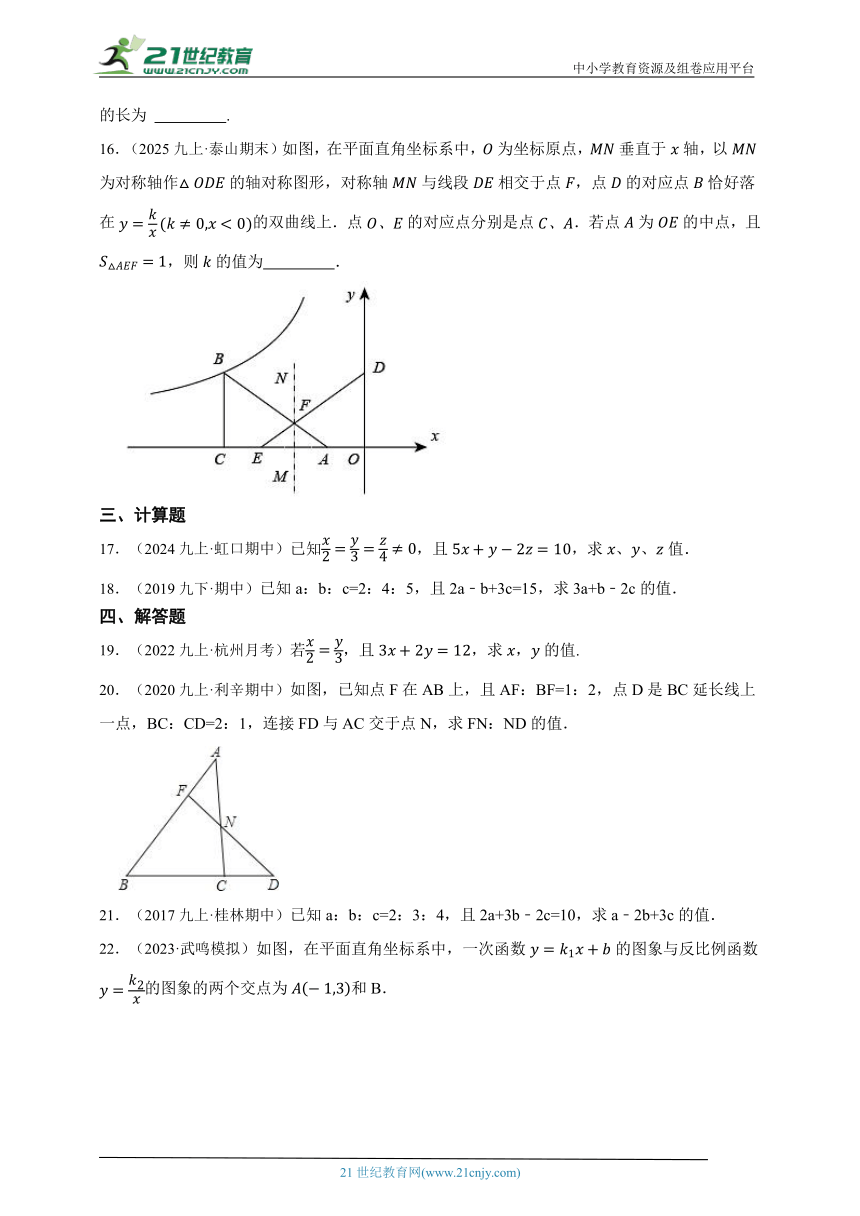
13.(2023九上·市中区期末)如图,直线,直线,与这三条平行线分别交于点A,B,C和点D,E,F,若,,则的长为 .
14.(2025·茂名模拟)如图直线,若,,则 .
15.(2022九上·杭州期中)若C是线段的黄金分割点(),若,则线段的长为 .
16.(2025九上·泰山期末)如图,在平面直角坐标系中,为坐标原点,垂直于轴,以为对称轴作的轴对称图形,对称轴与线段相交于点,点的对应点恰好落在的双曲线上.点的对应点分别是点.若点为的中点,且,则的值为 .
三、计算题
17.(2024九上·虹口期中)已知,且,求、、值.
18.(2019九下·期中)已知a:b:c=2:4:5,且2a﹣b+3c=15,求3a+b﹣2c的值.
四、解答题
19.(2022九上·杭州月考)若,且,求,的值.
20.(2020九上·利辛期中)如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
21.(2017九上·桂林期中)已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a﹣2b+3c的值.
22.(2023·武鸣模拟)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象的两个交点为和B.
(1)求反比例函数的关系式;
(2)若一次函数与x轴交于点C,且求出与b的值;
(3)若点F是直线上一点,F点的横坐标为m,连接,的面积记为S,当时,请直接写出值______.
答案解析部分
1.【答案】A
【知识点】黄金分割
2.【答案】C
【知识点】比例的性质
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】C
【知识点】黄金分割
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】黄金分割
9.【答案】A
【知识点】黄金分割
10.【答案】C
【知识点】菱形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例;尺规作图-作角的平分线;尺规作图-垂直平分线
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】黄金分割
13.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
14.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】
【知识点】黄金分割
16.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】,,
【知识点】比例的性质
18.【答案】解:由a:b:c=2:4:5,设a=2x,b=4x,c=5x.由2a﹣b+3c=15,得4x﹣4x+15x=15,解得x=1,a=2,b=4,c=5.3a+b﹣2c=3×2+4﹣2×5=0.
【知识点】比例的性质
19.【答案】解:设
则,
代入得:
解得:
∴,
【知识点】比例的性质
20.【答案】解:过点F作FE∥BD,交AC于点E,
∴ ,
∵AF:BF=1:2,
∴ = ,
∴ ,
即FE= BC,
∵BC:CD=2:1,
∴CD= BC,
∵FE∥BD,
∴ .
即FN:ND=2:3.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
21.【答案】解:∵a:b:c=2:3:4,
∴设a=2k,b=3k,c=4k,
而2a+3b-2c=10,
∴4k+9k-8k=10,解得k=2,
∴a=4,b=6,c=8,
∴a-2b+3c=4-12+24=16.
【知识点】代数式求值;比例的性质
22.【答案】(1)
(2),
(3)或
【知识点】待定系数法求反比例函数解析式;两条直线被一组平行线所截,所得的对应线段成比例
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.1 成比例线段本届综合题
一、单选题
1.(2024九上·通州期中)鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工,如图,P是的黄金分割点(),那么( )
A. B. C. D.
2.(2025九上·赣榆期末)王老师的电脑显示器分辨率为,当她全屏浏览尺寸为(“”表示像素)的图片时,由于不成比例(),画面两边会出现黑色区域,若成比例就不会出现此问题,王老师全屏浏览以下四种尺寸的图片时,画面四周都不会出现黑边的是( )
A. B.
C. D.
3.(2024九上·西湖月考)如图,直线,分别交直线,于点,,,,,.若,,则的长为( )
A.4 B.5 C.6 D.10
4.(2024八下·苏州工业园月考)如图,在中,,若,,则的长为( )
A.4 B.6 C.8 D.10
5.(2025九上·路桥期末)如图,,若,,则的长为( )
A.6 B.9 C.12 D.15
6.(2022九上·江干月考)如图,已知线段AB=2,点P是线段AB的黄金分割点(AP
7.(2020九上·亳州期中)AD 是△ABC 的中线,E 是 AD 上一点,AE= AD,BE 的延长线交 AC 于 F,则 的值为( )
A. B. C. D.
8.(2020九上·马鞍山期末)若点 为线段 的黄金分割点,且 ,则下列各式中错误的是( )
A. B.
C. D.
9.(2023九上·萧山期中)一本书的宽与长之比为黄金比,书的宽为14cm,则它的长为( )cm.
A.7+7 B.21-7 C.7-7 D.7-21
10.如图,已知.
⑴以点为圆心,以适当长为半径画弧,交于点,交于点.
⑵分别以为圆心,以大于的长为半径画弧,两弧在的内部相交于点.
⑶作射线交于点.
⑷分别以为圆心,以大于的长为半径画弧,两弧相交于两点.
⑸作直线,分别交于点.
依据以上作图,若,则的长是____.
A. B.1 C. D.4
二、填空题
11.(2023九上·崇明期中)若,且,那么 .
12.(2024九下·泰兴月考)已知P是线段的黄金分割点,且,则的值是 .
13.(2023九上·市中区期末)如图,直线,直线,与这三条平行线分别交于点A,B,C和点D,E,F,若,,则的长为 .
14.(2025·茂名模拟)如图直线,若,,则 .
15.(2022九上·杭州期中)若C是线段的黄金分割点(),若,则线段的长为 .
16.(2025九上·泰山期末)如图,在平面直角坐标系中,为坐标原点,垂直于轴,以为对称轴作的轴对称图形,对称轴与线段相交于点,点的对应点恰好落在的双曲线上.点的对应点分别是点.若点为的中点,且,则的值为 .
三、计算题
17.(2024九上·虹口期中)已知,且,求、、值.
18.(2019九下·期中)已知a:b:c=2:4:5,且2a﹣b+3c=15,求3a+b﹣2c的值.
四、解答题
19.(2022九上·杭州月考)若,且,求,的值.
20.(2020九上·利辛期中)如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
21.(2017九上·桂林期中)已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a﹣2b+3c的值.
22.(2023·武鸣模拟)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象的两个交点为和B.
(1)求反比例函数的关系式;
(2)若一次函数与x轴交于点C,且求出与b的值;
(3)若点F是直线上一点,F点的横坐标为m,连接,的面积记为S,当时,请直接写出值______.
答案解析部分
1.【答案】A
【知识点】黄金分割
2.【答案】C
【知识点】比例的性质
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】C
【知识点】黄金分割
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】黄金分割
9.【答案】A
【知识点】黄金分割
10.【答案】C
【知识点】菱形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例;尺规作图-作角的平分线;尺规作图-垂直平分线
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】黄金分割
13.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
14.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】
【知识点】黄金分割
16.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】,,
【知识点】比例的性质
18.【答案】解:由a:b:c=2:4:5,设a=2x,b=4x,c=5x.由2a﹣b+3c=15,得4x﹣4x+15x=15,解得x=1,a=2,b=4,c=5.3a+b﹣2c=3×2+4﹣2×5=0.
【知识点】比例的性质
19.【答案】解:设
则,
代入得:
解得:
∴,
【知识点】比例的性质
20.【答案】解:过点F作FE∥BD,交AC于点E,
∴ ,
∵AF:BF=1:2,
∴ = ,
∴ ,
即FE= BC,
∵BC:CD=2:1,
∴CD= BC,
∵FE∥BD,
∴ .
即FN:ND=2:3.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
21.【答案】解:∵a:b:c=2:3:4,
∴设a=2k,b=3k,c=4k,
而2a+3b-2c=10,
∴4k+9k-8k=10,解得k=2,
∴a=4,b=6,c=8,
∴a-2b+3c=4-12+24=16.
【知识点】代数式求值;比例的性质
22.【答案】(1)
(2),
(3)或
【知识点】待定系数法求反比例函数解析式;两条直线被一组平行线所截,所得的对应线段成比例
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
