23.3 相似三角形综合题 同步练习(含答案)
文档属性
| 名称 | 23.3 相似三角形综合题 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 575.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:48:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
23.3 相似三角形本节综合题
一、单选题
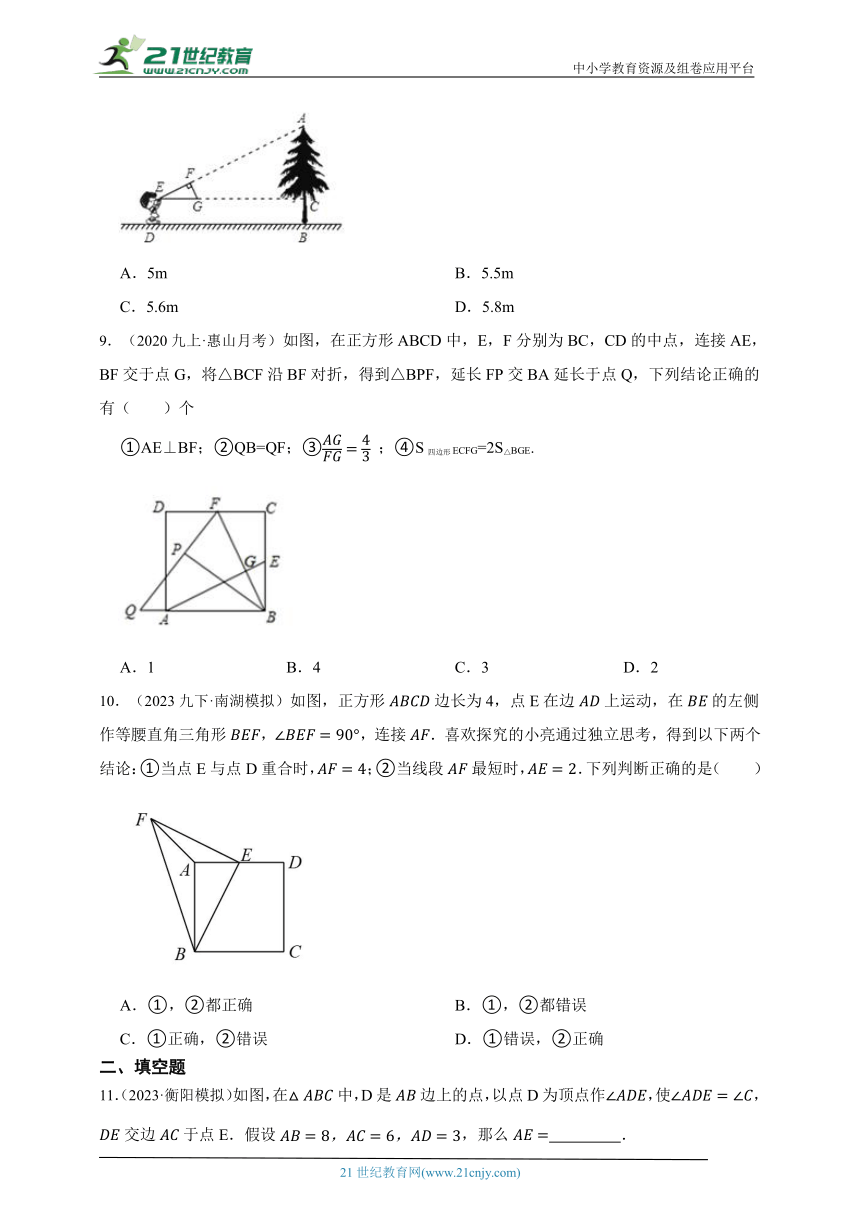
1.(2024九上·辽宁期中)如图,在中,,若,,,则的长为( )
A.4 B.6 C.8 D.9
2.(2024九上·长春月考)在中,,用直尺和圆规在边上确定一点D,使,根据下列作图痕迹判断,正确的是( )
A. B.
C. D.
3.(2024九下·深圳期末)击地传球是篮球运动中的一种传球方式,利用击地传球可以有效地躲避对手的拦截.传球选手从点处将球传出,经地面点处反弹后被接球选手在点处接住,将球所经过的路径视为直线,此时.若点距地面的高度为,点距地面的高度为,传球选手与接球选手之间的距离为,则的长度为( )
A. B. C. D.
4.(2025九下·南京开学考)如图,在中,,则下列结论正确的是( )
A.
B.
C.
D.
5.两个相似三角形面积比为1:3,他们对应高的比为( )
A.1:3 B.1: C.1:9 D.:1
6.(2019九上·滦南期中)如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则 为( )
A. B. C. D.
7.(2024九上·未央期末)如图,在中,,若,,则=( )
A. B. C. D.
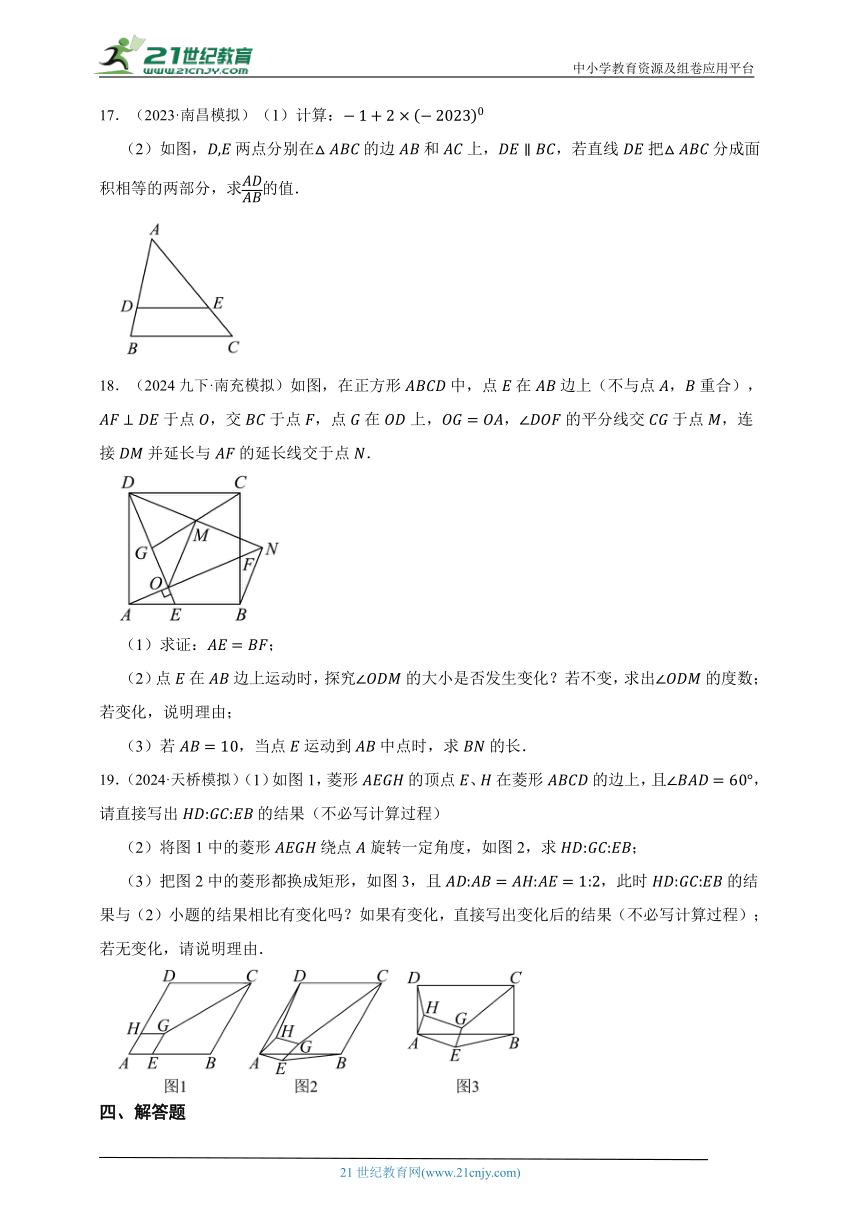
8.如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
A.5m B.5.5m
C.5.6m D.5.8m
9.(2020九上·惠山月考)如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个
①AE⊥BF;②QB=QF;③ ;④S四边形ECFG=2S△BGE.
A.1 B.4 C.3 D.2
10.(2023九下·南湖模拟)如图,正方形边长为4,点E在边上运动,在的左侧作等腰直角三角形,,连接.喜欢探究的小亮通过独立思考,得到以下两个结论:①当点E与点D重合时,;②当线段最短时,.下列判断正确的是( )
A.①,②都正确 B.①,②都错误
C.①正确,②错误 D.①错误,②正确
二、填空题
11.(2023·衡阳模拟)如图,在中,D是边上的点,以点D为顶点作,使,交边于点E.假设,那么 .
12.(2024八上·东台期中)已知,,,则的度数为 .
13.(2023九上·上海市月考)如图,△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,,若AC=10,AE=4,则BC= .
14.(2021九上·渠县期末)墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= .
15.(2022·和平模拟)如图,则x= ,y= .
16.(2024九下·哈尔滨月考)如图,在中,是的高,点E在上,,点G在上, 交于点F,若,则的长为 .
三、计算题
17.(2023·南昌模拟)(1)计算:
(2)如图,两点分别在的边和上,,若直线把分成面积相等的两部分,求的值.
18.(2024九下·南充模拟)如图,在正方形中,点在边上(不与点,重合),于点,交于点,点在上,,的平分线交于点,连接并延长与的延长线交于点.
(1)求证:;
(2)点在边上运动时,探究的大小是否发生变化?若不变,求出的度数;若变化,说明理由;
(3)若,当点运动到中点时,求的长.
19.(2024·天桥模拟)(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
20.(2024九上·杭州月考)如图,,分别是、上的点.
(1)求、的度数.
(2)若,,则是的几倍?
21.(2022九上·碧江月考)如图,,动点,分别以每秒和的速度同时开始运动,其中点从点出发,沿边一直移到点为止,点从点出发沿边一直运动到点为止(点到达点后,点继续运动)
(1)请直接用含的代数式表示的长和的长,并写出的取值范围;
(2)当等于何值时,与相似?
22.(2022九上·雁塔月考)小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图.小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在地上的影子高度,,(点A、E、C在同一直线上).已知小明的身高是1.7m.请你帮小明求出楼高.
23.(2024·淮安模拟)如图,平行四边形面积为24,其中为锐角.点P是边上的一动点.
(1)如图1,点P到边上的距离为 ;
(2)当点A,D同时绕点P按顺时针方向旋转90°得点,
①如图2,当落在射线上时,求的长;
②当是直角三角形时,直接写出的长.
答案解析部分
1.【答案】B
【知识点】相似三角形的判定与性质
2.【答案】C
【知识点】相似三角形的判定;尺规作图-作一个角等于已知角;尺规作图-作角的平分线;尺规作图-垂直平分线
3.【答案】D
【知识点】相似三角形的应用
4.【答案】C
【知识点】相似三角形的判定与性质
5.【答案】B
【知识点】相似三角形的性质
6.【答案】D
【知识点】相似三角形的判定与性质
7.【答案】D
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】相似三角形的应用
9.【答案】C
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
10.【答案】A
【知识点】等腰三角形的性质;正方形的性质;相似三角形的判定与性质
11.【答案】4
【知识点】相似三角形的判定与性质
12.【答案】
【知识点】三角形内角和定理;相似三角形的性质
13.【答案】15
【知识点】等腰三角形的判定与性质;相似三角形的判定与性质;内错角的概念
14.【答案】 m
【知识点】相似三角形的判定与性质;中心投影
15.【答案】;98
【知识点】相似三角形的判定与性质
16.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;相似三角形的判定与性质
17.【答案】(1)1;(2).
【知识点】零指数幂;相似三角形的判定与性质
18.【答案】(1)证明见解答过程
(2)的大小不会变化,
(3)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;相似三角形的判定与性质
19.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
20.【答案】(1)
(2)是的2倍
【知识点】三角形内角和定理;相似三角形的判定与性质
21.【答案】(1)AP=2tcm(),AQ=(16-t)cm()
(2)或
【知识点】相似三角形的性质
22.【答案】解:过点D作DG⊥AB,分别交AB、EF于点G、H,
∵ABCD,DG⊥AB,AB⊥AC,
∴四边形ACDG是矩形,
∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,
∵EFAB,
∴,
∴,
由题意,知FH=EF EH=1.7 1.2=0.5,
∴,
解得,BG=18.75(m),
∴AB=BG+AG=18.75+1.2=19.95(m).
∴楼高AB为19.95(m).
【知识点】相似三角形的应用
23.【答案】(1)4
(2)①;②,,
【知识点】平行四边形的性质;相似三角形的判定与性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.3 相似三角形本节综合题
一、单选题
1.(2024九上·辽宁期中)如图,在中,,若,,,则的长为( )
A.4 B.6 C.8 D.9
2.(2024九上·长春月考)在中,,用直尺和圆规在边上确定一点D,使,根据下列作图痕迹判断,正确的是( )
A. B.
C. D.
3.(2024九下·深圳期末)击地传球是篮球运动中的一种传球方式,利用击地传球可以有效地躲避对手的拦截.传球选手从点处将球传出,经地面点处反弹后被接球选手在点处接住,将球所经过的路径视为直线,此时.若点距地面的高度为,点距地面的高度为,传球选手与接球选手之间的距离为,则的长度为( )
A. B. C. D.
4.(2025九下·南京开学考)如图,在中,,则下列结论正确的是( )
A.
B.
C.
D.
5.两个相似三角形面积比为1:3,他们对应高的比为( )
A.1:3 B.1: C.1:9 D.:1
6.(2019九上·滦南期中)如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则 为( )
A. B. C. D.
7.(2024九上·未央期末)如图,在中,,若,,则=( )
A. B. C. D.
8.如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
A.5m B.5.5m
C.5.6m D.5.8m
9.(2020九上·惠山月考)如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个
①AE⊥BF;②QB=QF;③ ;④S四边形ECFG=2S△BGE.
A.1 B.4 C.3 D.2
10.(2023九下·南湖模拟)如图,正方形边长为4,点E在边上运动,在的左侧作等腰直角三角形,,连接.喜欢探究的小亮通过独立思考,得到以下两个结论:①当点E与点D重合时,;②当线段最短时,.下列判断正确的是( )
A.①,②都正确 B.①,②都错误
C.①正确,②错误 D.①错误,②正确
二、填空题
11.(2023·衡阳模拟)如图,在中,D是边上的点,以点D为顶点作,使,交边于点E.假设,那么 .
12.(2024八上·东台期中)已知,,,则的度数为 .
13.(2023九上·上海市月考)如图,△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,,若AC=10,AE=4,则BC= .
14.(2021九上·渠县期末)墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= .
15.(2022·和平模拟)如图,则x= ,y= .
16.(2024九下·哈尔滨月考)如图,在中,是的高,点E在上,,点G在上, 交于点F,若,则的长为 .
三、计算题
17.(2023·南昌模拟)(1)计算:
(2)如图,两点分别在的边和上,,若直线把分成面积相等的两部分,求的值.
18.(2024九下·南充模拟)如图,在正方形中,点在边上(不与点,重合),于点,交于点,点在上,,的平分线交于点,连接并延长与的延长线交于点.
(1)求证:;
(2)点在边上运动时,探究的大小是否发生变化?若不变,求出的度数;若变化,说明理由;
(3)若,当点运动到中点时,求的长.
19.(2024·天桥模拟)(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
四、解答题
20.(2024九上·杭州月考)如图,,分别是、上的点.
(1)求、的度数.
(2)若,,则是的几倍?
21.(2022九上·碧江月考)如图,,动点,分别以每秒和的速度同时开始运动,其中点从点出发,沿边一直移到点为止,点从点出发沿边一直运动到点为止(点到达点后,点继续运动)
(1)请直接用含的代数式表示的长和的长,并写出的取值范围;
(2)当等于何值时,与相似?
22.(2022九上·雁塔月考)小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图.小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在地上的影子高度,,(点A、E、C在同一直线上).已知小明的身高是1.7m.请你帮小明求出楼高.
23.(2024·淮安模拟)如图,平行四边形面积为24,其中为锐角.点P是边上的一动点.
(1)如图1,点P到边上的距离为 ;
(2)当点A,D同时绕点P按顺时针方向旋转90°得点,
①如图2,当落在射线上时,求的长;
②当是直角三角形时,直接写出的长.
答案解析部分
1.【答案】B
【知识点】相似三角形的判定与性质
2.【答案】C
【知识点】相似三角形的判定;尺规作图-作一个角等于已知角;尺规作图-作角的平分线;尺规作图-垂直平分线
3.【答案】D
【知识点】相似三角形的应用
4.【答案】C
【知识点】相似三角形的判定与性质
5.【答案】B
【知识点】相似三角形的性质
6.【答案】D
【知识点】相似三角形的判定与性质
7.【答案】D
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】相似三角形的应用
9.【答案】C
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
10.【答案】A
【知识点】等腰三角形的性质;正方形的性质;相似三角形的判定与性质
11.【答案】4
【知识点】相似三角形的判定与性质
12.【答案】
【知识点】三角形内角和定理;相似三角形的性质
13.【答案】15
【知识点】等腰三角形的判定与性质;相似三角形的判定与性质;内错角的概念
14.【答案】 m
【知识点】相似三角形的判定与性质;中心投影
15.【答案】;98
【知识点】相似三角形的判定与性质
16.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;相似三角形的判定与性质
17.【答案】(1)1;(2).
【知识点】零指数幂;相似三角形的判定与性质
18.【答案】(1)证明见解答过程
(2)的大小不会变化,
(3)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;相似三角形的判定与性质
19.【答案】(1);(2)(3)有变化,
【知识点】菱形的性质;相似三角形的判定与性质
20.【答案】(1)
(2)是的2倍
【知识点】三角形内角和定理;相似三角形的判定与性质
21.【答案】(1)AP=2tcm(),AQ=(16-t)cm()
(2)或
【知识点】相似三角形的性质
22.【答案】解:过点D作DG⊥AB,分别交AB、EF于点G、H,
∵ABCD,DG⊥AB,AB⊥AC,
∴四边形ACDG是矩形,
∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,
∵EFAB,
∴,
∴,
由题意,知FH=EF EH=1.7 1.2=0.5,
∴,
解得,BG=18.75(m),
∴AB=BG+AG=18.75+1.2=19.95(m).
∴楼高AB为19.95(m).
【知识点】相似三角形的应用
23.【答案】(1)4
(2)①;②,,
【知识点】平行四边形的性质;相似三角形的判定与性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
