23.3.4 相似三角形的应用 同步练习(含答案)
文档属性
| 名称 | 23.3.4 相似三角形的应用 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 641.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 16:04:55 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4. 相似三角形的应用
一、单选题
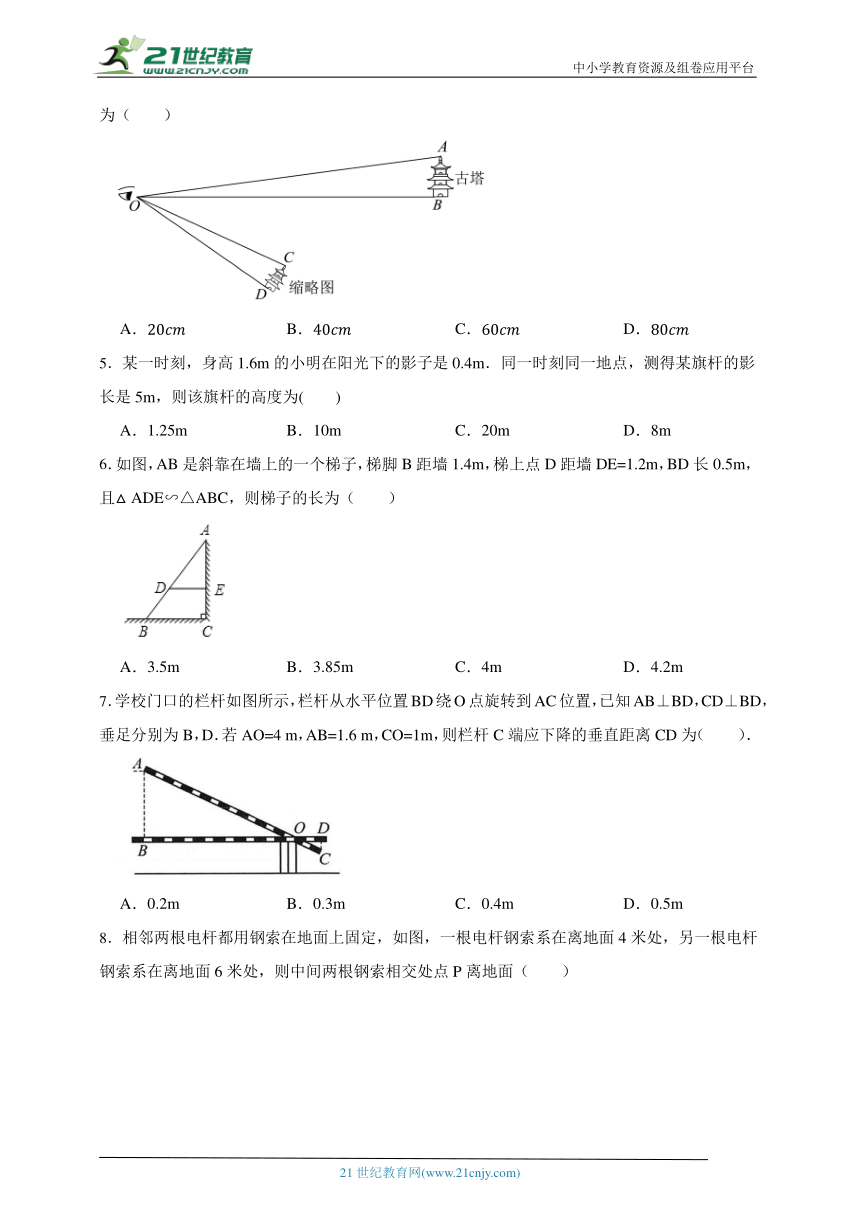
1.(2024九上·浦东期中)如图,是凸透镜的主光轴,点O是光心,点F是焦点.若蜡烛的像为, 测量得到, 蜡烛高为, 则像的长为( )
A. B. C. D.
2.(2023九上·天桥期中)如图,在平行四边形中,点E在边上,,连接交于点F,则的面积与的面积之比为( )
A. B. C. D.
3.(2024八下·淄博期中)如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为,旗杆底部与平面镜的水平距离为.若小明的眼睛与地面的距离为,则旗杆的高度为(单位:m)( )
A.12.4 B.12.5 C.12.8 D.16
4.(2024九上·澧县期中)如图,周末小新一家来到河北石家庄正定古城游元,一座古塔塔高为,小新在距离古塔的位置观看古塔时,与观看到的手中的景点地图的古塔缩略图感觉相同(),若缩略图中的古塔高为,则缩略图距离眼睛的距离为( )
A. B. C. D.
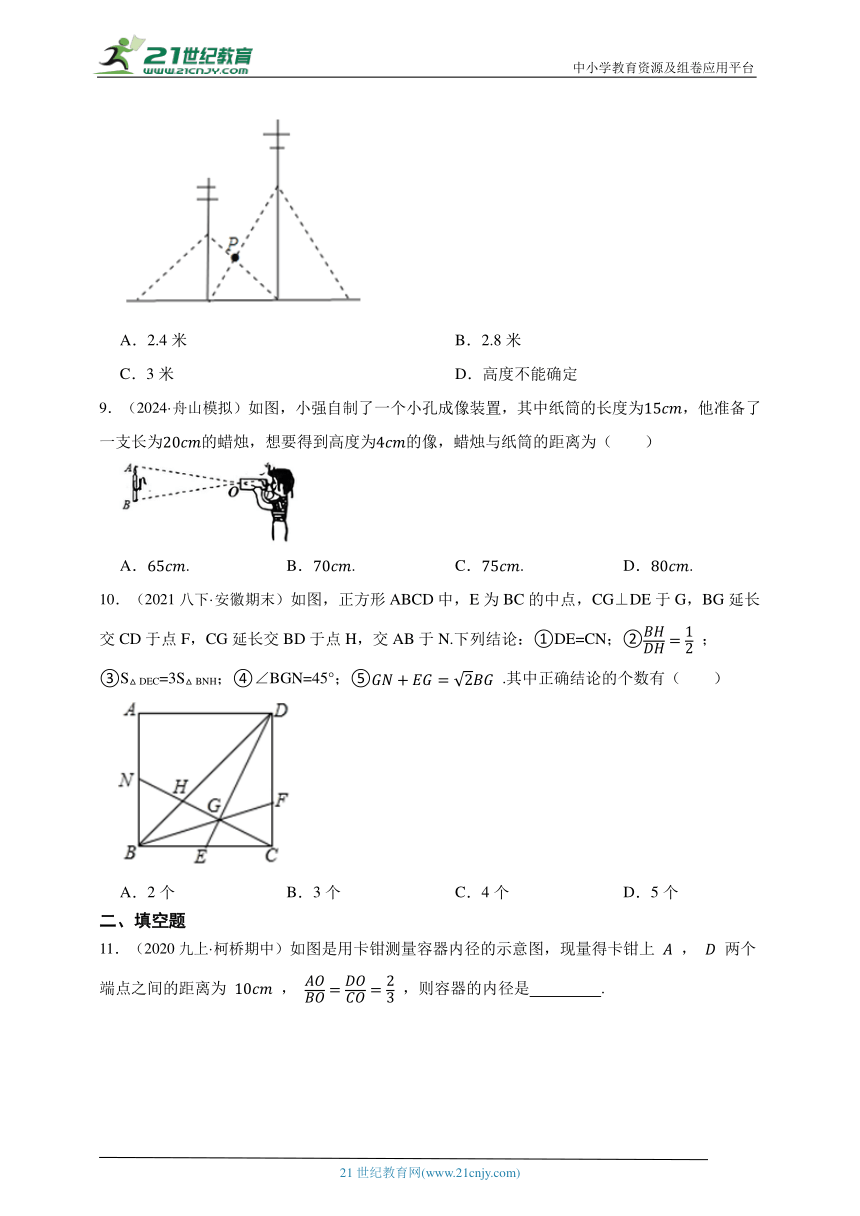
5.某一时刻,身高1.6m的小明在阳光下的影子是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度为( )
A.1.25m B.10m C.20m D.8m
6.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
7.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D.若AO=4 m,AB=1.6 m,CO=1m,则栏杆C端应下降的垂直距离CD为( ).
A.0.2m B.0.3m C.0.4m D.0.5m
8.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
A.2.4米 B.2.8米
C.3米 D.高度不能确定
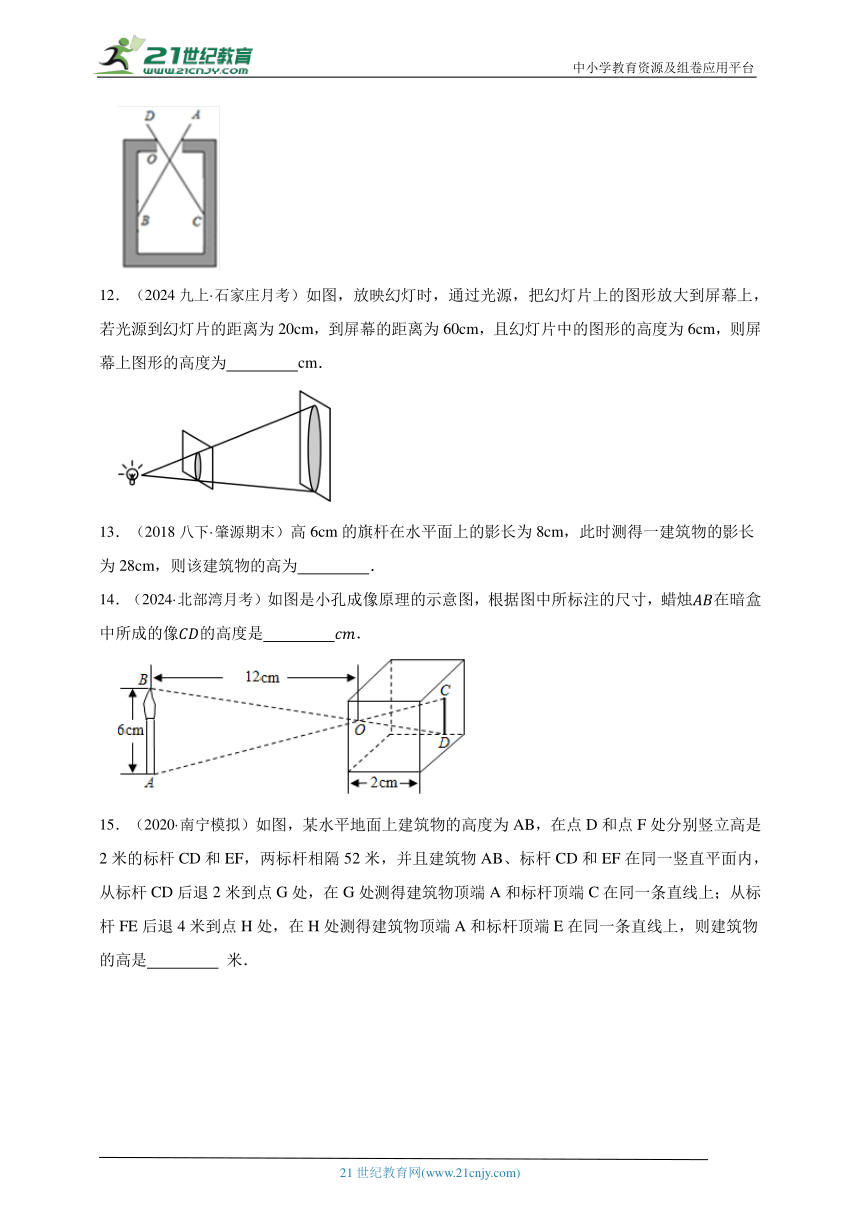
9.(2024·舟山模拟)如图,小强自制了一个小孔成像装置,其中纸筒的长度为,他准备了一支长为的蜡烛,想要得到高度为的像,蜡烛与纸筒的距离为( )
A.. B.. C.. D..
10.(2021八下·安徽期末)如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;② ;③S△DEC=3S△BNH;④∠BGN=45°;⑤ .其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.(2020九上·柯桥期中)如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是 .
12.(2024九上·石家庄月考)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
13.(2018八下·肇源期末)高6cm的旗杆在水平面上的影长为8cm,此时测得一建筑物的影长为28cm,则该建筑物的高为 .
14.(2024·北部湾月考)如图是小孔成像原理的示意图,根据图中所标注的尺寸,蜡烛在暗盒中所成的像的高度是 .
15.(2020·南宁模拟)如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
16.(2017·历下模拟)如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号).
①∠NAP=45°;
②当P为BC中点时,AE为线段NP的中垂线;
③四边形AMCB的面积最大值为10;
④线段AM的最小值为2 ;
⑤当△ABP≌△ADN时,BP=4 ﹣4.
三、计算题
17.(2023九上·茌平月考)有一块三角形余料,它的边,高,要把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,求加工成的正方形零件的边长.
18.(2023九上·东兴期中)大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上处垂直于地面竖立了高度为2米的标杆,这时地面上的点,标杆的顶端点,大雁塔的塔尖点正好在同一直线上,测得米,将标杆向后平移到点处,这时地面上的点,标杆的顶端点,大雁塔的塔尖点正好在同一直线上(点,点,点,点与大雁塔底处的点在同一直线上),这时测得米,米,请你根据以上数据,计算大雁塔的高度.
四、解答题
19.(2025九下·荣县月考)如图,红红同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上,已知纸板的两条直角边,,测得边DF离地面的高度,,求树高.
20.(2024九上·南湖月考)学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米,小丽先调整自己的位置至点P,将直角三角形纸板的三个顶点位置记为A、B、C(如图),斜边平行于地面(点M、P、E、N在一条直线上),且点D在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度.
21.(2022九上·交城期末)5月10日上午,庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行,习近平总书记重要讲话引发各界青年热烈反响.某校为庆祝共青团成立100周年升起了共青团旗帜,李优和贺基旭想用所学知识测量该旗帜的宽度MN,他们进行了如下操作:如图,首先,李优在C处竖立一根标杆,地面上的点A、标杆顶端B和点N在一条直线上,米,米,米;然后,贺基旭手持自制直角三角纸板,使长直角边与水平地面平行,调整位置,恰好在P点时点D、E、M在一条直线上,米,米,,已知,,,点P、G、C、A在同一水平直线上,点N在上,求旗帜的宽度.
22.(2024九上·怀化期末)某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F,标B杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB.
答案解析部分
1.【答案】C
【知识点】相似三角形的应用
2.【答案】C
【知识点】相似三角形的应用
3.【答案】C
【知识点】相似三角形的应用
4.【答案】A
【知识点】相似三角形的判定与性质;相似三角形的应用
5.【答案】C
【知识点】相似三角形的应用
6.【答案】A
【知识点】相似三角形的应用
7.【答案】C
【知识点】相似三角形的应用
8.【答案】A
【知识点】相似三角形的应用
9.【答案】C
【知识点】相似三角形的应用
10.【答案】D
【知识点】全等三角形的应用;相似三角形的应用
11.【答案】15cm
【知识点】相似三角形的应用
12.【答案】18
【知识点】相似三角形的应用
13.【答案】21
【知识点】相似三角形的应用
14.【答案】1
【知识点】相似三角形的应用
15.【答案】54
【知识点】相似三角形的应用
16.【答案】①③⑤
【知识点】全等三角形的应用;相似三角形的应用
17.【答案】mm
【知识点】相似三角形的判定与性质;相似三角形的应用
18.【答案】AB=62米
【知识点】相似三角形的应用
19.【答案】
【知识点】相似三角形的应用
20.【答案】古树的高度是米
【知识点】相似三角形的应用
21.【答案】解:如图,延长交于Q,则,,
∵,,
∴,
∴∽,
∴,即
∴,
同理得:∽,
∴,
∵,
∴,
∴(米).
答:旗帜的宽度是1.3米.
【知识点】相似三角形的应用
22.【答案】解:由题意得:,,
∴,,
,
∴,
,
(米),
∵,
∴,
(米),
答:古塔的高度为22米.
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4. 相似三角形的应用
一、单选题
1.(2024九上·浦东期中)如图,是凸透镜的主光轴,点O是光心,点F是焦点.若蜡烛的像为, 测量得到, 蜡烛高为, 则像的长为( )
A. B. C. D.
2.(2023九上·天桥期中)如图,在平行四边形中,点E在边上,,连接交于点F,则的面积与的面积之比为( )
A. B. C. D.
3.(2024八下·淄博期中)如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为,旗杆底部与平面镜的水平距离为.若小明的眼睛与地面的距离为,则旗杆的高度为(单位:m)( )
A.12.4 B.12.5 C.12.8 D.16
4.(2024九上·澧县期中)如图,周末小新一家来到河北石家庄正定古城游元,一座古塔塔高为,小新在距离古塔的位置观看古塔时,与观看到的手中的景点地图的古塔缩略图感觉相同(),若缩略图中的古塔高为,则缩略图距离眼睛的距离为( )
A. B. C. D.
5.某一时刻,身高1.6m的小明在阳光下的影子是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度为( )
A.1.25m B.10m C.20m D.8m
6.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
7.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D.若AO=4 m,AB=1.6 m,CO=1m,则栏杆C端应下降的垂直距离CD为( ).
A.0.2m B.0.3m C.0.4m D.0.5m
8.相邻两根电杆都用钢索在地面上固定,如图,一根电杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,则中间两根钢索相交处点P离地面( )
A.2.4米 B.2.8米
C.3米 D.高度不能确定
9.(2024·舟山模拟)如图,小强自制了一个小孔成像装置,其中纸筒的长度为,他准备了一支长为的蜡烛,想要得到高度为的像,蜡烛与纸筒的距离为( )
A.. B.. C.. D..
10.(2021八下·安徽期末)如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;② ;③S△DEC=3S△BNH;④∠BGN=45°;⑤ .其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.(2020九上·柯桥期中)如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是 .
12.(2024九上·石家庄月考)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
13.(2018八下·肇源期末)高6cm的旗杆在水平面上的影长为8cm,此时测得一建筑物的影长为28cm,则该建筑物的高为 .
14.(2024·北部湾月考)如图是小孔成像原理的示意图,根据图中所标注的尺寸,蜡烛在暗盒中所成的像的高度是 .
15.(2020·南宁模拟)如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
16.(2017·历下模拟)如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号).
①∠NAP=45°;
②当P为BC中点时,AE为线段NP的中垂线;
③四边形AMCB的面积最大值为10;
④线段AM的最小值为2 ;
⑤当△ABP≌△ADN时,BP=4 ﹣4.
三、计算题
17.(2023九上·茌平月考)有一块三角形余料,它的边,高,要把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,求加工成的正方形零件的边长.
18.(2023九上·东兴期中)大雁塔是现存最早规模最大的唐代四方楼阁式砖塔,被国务院批准列入第一批全国重点文物保护单位,某校社会实践小组为了测量大雁塔的高度,在地面上处垂直于地面竖立了高度为2米的标杆,这时地面上的点,标杆的顶端点,大雁塔的塔尖点正好在同一直线上,测得米,将标杆向后平移到点处,这时地面上的点,标杆的顶端点,大雁塔的塔尖点正好在同一直线上(点,点,点,点与大雁塔底处的点在同一直线上),这时测得米,米,请你根据以上数据,计算大雁塔的高度.
四、解答题
19.(2025九下·荣县月考)如图,红红同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上,已知纸板的两条直角边,,测得边DF离地面的高度,,求树高.
20.(2024九上·南湖月考)学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米,小丽先调整自己的位置至点P,将直角三角形纸板的三个顶点位置记为A、B、C(如图),斜边平行于地面(点M、P、E、N在一条直线上),且点D在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度.
21.(2022九上·交城期末)5月10日上午,庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行,习近平总书记重要讲话引发各界青年热烈反响.某校为庆祝共青团成立100周年升起了共青团旗帜,李优和贺基旭想用所学知识测量该旗帜的宽度MN,他们进行了如下操作:如图,首先,李优在C处竖立一根标杆,地面上的点A、标杆顶端B和点N在一条直线上,米,米,米;然后,贺基旭手持自制直角三角纸板,使长直角边与水平地面平行,调整位置,恰好在P点时点D、E、M在一条直线上,米,米,,已知,,,点P、G、C、A在同一水平直线上,点N在上,求旗帜的宽度.
22.(2024九上·怀化期末)某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F,标B杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB.
答案解析部分
1.【答案】C
【知识点】相似三角形的应用
2.【答案】C
【知识点】相似三角形的应用
3.【答案】C
【知识点】相似三角形的应用
4.【答案】A
【知识点】相似三角形的判定与性质;相似三角形的应用
5.【答案】C
【知识点】相似三角形的应用
6.【答案】A
【知识点】相似三角形的应用
7.【答案】C
【知识点】相似三角形的应用
8.【答案】A
【知识点】相似三角形的应用
9.【答案】C
【知识点】相似三角形的应用
10.【答案】D
【知识点】全等三角形的应用;相似三角形的应用
11.【答案】15cm
【知识点】相似三角形的应用
12.【答案】18
【知识点】相似三角形的应用
13.【答案】21
【知识点】相似三角形的应用
14.【答案】1
【知识点】相似三角形的应用
15.【答案】54
【知识点】相似三角形的应用
16.【答案】①③⑤
【知识点】全等三角形的应用;相似三角形的应用
17.【答案】mm
【知识点】相似三角形的判定与性质;相似三角形的应用
18.【答案】AB=62米
【知识点】相似三角形的应用
19.【答案】
【知识点】相似三角形的应用
20.【答案】古树的高度是米
【知识点】相似三角形的应用
21.【答案】解:如图,延长交于Q,则,,
∵,,
∴,
∴∽,
∴,即
∴,
同理得:∽,
∴,
∵,
∴,
∴(米).
答:旗帜的宽度是1.3米.
【知识点】相似三角形的应用
22.【答案】解:由题意得:,,
∴,,
,
∴,
,
(米),
∵,
∴,
(米),
答:古塔的高度为22米.
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
