2.1.1 有理数的加法 同步练习(含答案)
文档属性
| 名称 | 2.1.1 有理数的加法 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 297.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 16:31:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.1.1 有理数的加法
一、单选题
1.2的相反数与0.5的绝对值的和是( )
A.2.5 B.1.5 C.-1.5 D.-2.5
2.(2024七上·广西壮族自治区期中) 把笔尖放在数轴的原点,沿数轴先向左移动5个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A. B. C. D.
3.(2024七上·澧县期中)计算:的结果是( )
A. B.4 C. D.8
4.(2025·井研模拟)计算( )
A. B. C. D.
5.(2024七上·茂名开学考)绝对值小于4的负整数之和是( )
A. B.0 C.4 D.6
6.(2020七上·沈阳月考)计算 时运算律用得最合理的是( )
A. B.
C. D.
7.下列问题情境,不能用加法算式-2+10表示的是( )
A.水位先下降2cm,再上升10cm后的水位变化情况
B.某日最低气温为-2℃,温差为10℃,该日最高气温
C.用10元纸币购买2元文具后找回的零钱
D.数轴上表示-2与10的两个点之间的距离
8.(2024七下·江城期中)若,,且,则的值等于( )
A.1或5 B.1或 C.或 D.或5
9.(2023七上·洪雅期中)我们知道,的几何意义是:数轴上表示数的点到原点的距离,可以理解为,进一步地,数轴上,表示数的点到表示数的点的距离可以用表示,例如:表示和的两点之间的距离是.根据绝对值的几何意义,当取最小值时,求出所有满足条件的整数的和为( )
A. B. C. D.
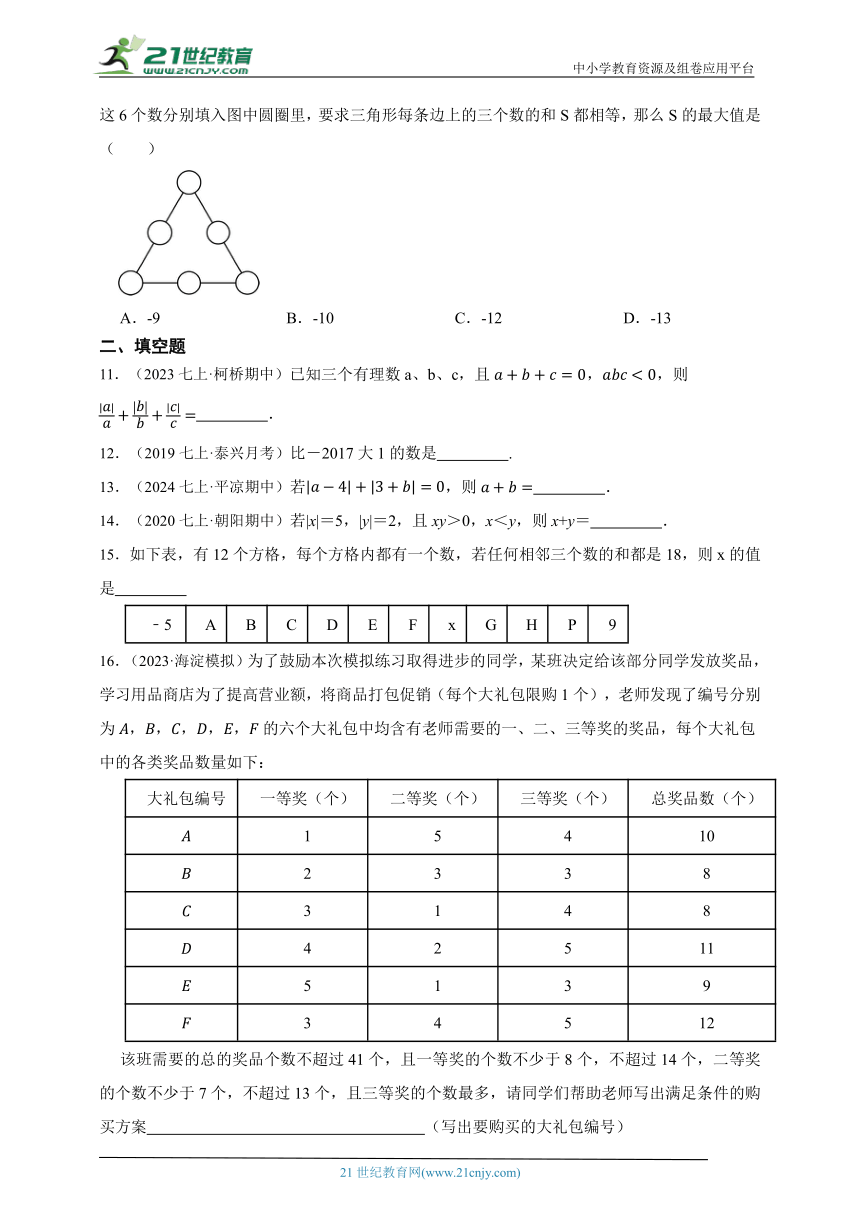
10.(2024七上·崇川月考)如图,在一个由六个圆圈组成的三角形里,把-1,-2,-3,-4,-5,-6这6个数分别填入图中圆圈里,要求三角形每条边上的三个数的和S都相等,那么S的最大值是( )
A.-9 B.-10 C.-12 D.-13
二、填空题
11.(2023七上·柯桥期中)已知三个有理数a、b、c,且,,则 .
12.(2019七上·泰兴月考)比-2017大1的数是 .
13.(2024七上·平凉期中)若,则 .
14.(2020七上·朝阳期中)若|x|=5,|y|=2,且xy>0,x<y,则x+y= .
15.如下表,有12个方格,每个方格内都有一个数,若任何相邻三个数的和都是18,则x的值是
﹣5 A B C D E F x G H P 9
16.(2023·海淀模拟)为了鼓励本次模拟练习取得进步的同学,某班决定给该部分同学发放奖品,学习用品商店为了提高营业额,将商品打包促销(每个大礼包限购1个),老师发现了编号分别为,,,,,的六个大礼包中均含有老师需要的一、二、三等奖的奖品,每个大礼包中的各类奖品数量如下:
大礼包编号 一等奖(个) 二等奖(个) 三等奖(个) 总奖品数(个)
1 5 4 10
2 3 3 8
3 1 4 8
4 2 5 11
5 1 3 9
3 4 5 12
该班需要的总的奖品个数不超过41个,且一等奖的个数不少于8个,不超过14个,二等奖的个数不少于7个,不超过13个,且三等奖的个数最多,请同学们帮助老师写出满足条件的购买方案 (写出要购买的大礼包编号)
三、计算题
17.计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)43+(﹣77)+27+(﹣43)
(3)18+(﹣16)+(﹣23)+16
(4)(﹣3)+(+7)+4+3+(﹣5)+(﹣4)
(5)5.6+(﹣0.9)+4.4+(﹣8.1)
(6)(﹣2)+17+(+12)+(﹣4)
18.(2021七上·峄城月考)用适当方法计算:
(1) ;
(2)
(3) ;
(4) .
19.(2022七上·西城月考)年,北京市燃油出租车具体收费标准如下:
①出租车收费标准公里以内收起步价元,再加1元燃油附加费,超过公里,超出部分按每公里元收费;
②预约叫车服务费:提前小时以上预约每次元,小时以内预约每次元;
③单程载客行驶超过公里的部分,按原价时段基本单价(元)加收的费用;
④出租车计价精确到米,超过米但不足米时按米计价,另外,每公里中的米计价元,后米计价按元.
⑤出租车收费结算以元为单位,精确到元(元以下四舍五入).
(注:如果车费不足起步价,则按起步价收费.)
结合以上信息,回答下列问题:
(1)已知肖老师家距离学校公里,周五早上肖老师为了避开早高峰选择时预约出租车出发,一路畅通到达学校,请你计算一下肖老师早上上班的出租车费用是 元;
(2)周五晚上,肖老师预约了周六上午乘出租车去机场,一路畅通到达机场,已知肖老师家距离机场(且为整数)公里,肖老师支付元(包括元高速收费站费用),则y= .
四、解答题
20.(2023七上·桑植期中)某检修小组乘汽车沿公路检修线路,约定往东为正,往西为负.某天自A地出发到收工时所走路线(单位:千米)为:,,,,,,,,,.
(1)问收工时距A地多远?在哪个方向?
(2)若每千米路程耗油m升,问从A地出发到收工共耗油多少升?
21.(2023七上·徐州月考)一辆汽车在一段东西向的公路来回巡查,若规定向东为正,向西为负,行驶的路程(千米)用正负数表示如下:,+4,,+8,,+12,;
(1)这辆车最后离开出发点的哪个方向?离开出发点多远?
(2)这辆车共行驶了多少千米?
22.若|a|=3,|b|=5,且a>b,求a+b的值.
23.(2023七上·惠阳月考)某一出租车一天下午以辰山植物园南门为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+10,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离出发点多远?在辰山植物园南门的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
答案解析部分
1.【答案】C
【知识点】有理数的加法
2.【答案】B
【知识点】有理数的加法;有理数在数轴上的表示
3.【答案】A
【知识点】有理数的加法法则
4.【答案】C
【知识点】有理数的加法法则
5.【答案】A
【知识点】绝对值的概念与意义;有理数的加法法则
6.【答案】D
【知识点】有理数的加法
7.【答案】D
【知识点】有理数的加法法则
8.【答案】A
【知识点】绝对值的概念与意义;有理数的加法法则
9.【答案】C
【知识点】数轴上两点之间的距离;绝对值的概念与意义;有理数的加法法则
10.【答案】A
【知识点】有理数的加法法则
11.【答案】1
【知识点】化简含绝对值有理数;有理数的加法法则
12.【答案】-2016
【知识点】有理数的加法
13.【答案】
【知识点】绝对值的非负性;有理数的加法法则
14.【答案】-7
【知识点】绝对值及有理数的绝对值;有理数的加法
15.【答案】14
【知识点】有理数的加法
16.【答案】各买一个(答案不唯一)
【知识点】有理数的加法实际应用
17.【答案】(1)解:(﹣3)+40+(﹣32)+(﹣8)
=40+[(﹣3)+(﹣32)+(﹣8)]
=40+(﹣43)
=﹣3
(2)解:43+(﹣77)+27+(﹣43)
=[(43+(﹣43)]+[(﹣77)+27]
=0+(﹣50)
=﹣50
(3)解:18+(﹣16)+(﹣23)+16
=(18+16)+[(﹣16)+(﹣23)]
=34+(﹣39)
=﹣5
(4)解:(﹣3)+(+7)+4+3+(﹣5)+(﹣4)
=[(+7)+4+3]+[(﹣3)+(﹣5)+(﹣4)]
=14+(﹣12)
=2,
(5)解:5.6+(﹣0.9)+4.4+(﹣8.1)
=(5.6+4.4)+[(﹣0.9)+(﹣8.1)]
=10+(﹣9)
=1,
(6)解:
=
=
=
【知识点】有理数的加法法则;有理数的加法运算律
18.【答案】(1)解:原式 ;
(2)解:原式 ;
(3)解:原式
;
(4)解:原式 .
【知识点】有理数的加法
19.【答案】(1)29
(2)
【知识点】有理数的加法法则
20.【答案】(1)解:
=
=-35+37
=2(千米)
答:收工时在正东方向,距离A地2千米.
(2)解:从A地出发到收工行驶的总路程为:
(千米),
∴从A地出发到收工共耗油升.
答:从A地出发到收工共耗油升
【知识点】正数、负数的实际应用;绝对值的概念与意义;有理数的加法实际应用
21.【答案】(1)这辆车最后离开出发点的正西方向,离开出发点10千米
(2)58千米
【知识点】正数、负数的实际应用;有理数的加法实际应用
22.【答案】解:∵|a|=3,|b|=5,且a>b,
∴a=3,b=﹣5;a=﹣3,b=﹣5,
则a+b=﹣2或﹣8
【知识点】相反数及有理数的相反数;有理数的加法
23.【答案】(1)在辰山植物园南门向东1km处;(2)司机一个下午的营业额是141.6元.
【知识点】有理数的加法实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.1.1 有理数的加法
一、单选题
1.2的相反数与0.5的绝对值的和是( )
A.2.5 B.1.5 C.-1.5 D.-2.5
2.(2024七上·广西壮族自治区期中) 把笔尖放在数轴的原点,沿数轴先向左移动5个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A. B. C. D.
3.(2024七上·澧县期中)计算:的结果是( )
A. B.4 C. D.8
4.(2025·井研模拟)计算( )
A. B. C. D.
5.(2024七上·茂名开学考)绝对值小于4的负整数之和是( )
A. B.0 C.4 D.6
6.(2020七上·沈阳月考)计算 时运算律用得最合理的是( )
A. B.
C. D.
7.下列问题情境,不能用加法算式-2+10表示的是( )
A.水位先下降2cm,再上升10cm后的水位变化情况
B.某日最低气温为-2℃,温差为10℃,该日最高气温
C.用10元纸币购买2元文具后找回的零钱
D.数轴上表示-2与10的两个点之间的距离
8.(2024七下·江城期中)若,,且,则的值等于( )
A.1或5 B.1或 C.或 D.或5
9.(2023七上·洪雅期中)我们知道,的几何意义是:数轴上表示数的点到原点的距离,可以理解为,进一步地,数轴上,表示数的点到表示数的点的距离可以用表示,例如:表示和的两点之间的距离是.根据绝对值的几何意义,当取最小值时,求出所有满足条件的整数的和为( )
A. B. C. D.
10.(2024七上·崇川月考)如图,在一个由六个圆圈组成的三角形里,把-1,-2,-3,-4,-5,-6这6个数分别填入图中圆圈里,要求三角形每条边上的三个数的和S都相等,那么S的最大值是( )
A.-9 B.-10 C.-12 D.-13
二、填空题
11.(2023七上·柯桥期中)已知三个有理数a、b、c,且,,则 .
12.(2019七上·泰兴月考)比-2017大1的数是 .
13.(2024七上·平凉期中)若,则 .
14.(2020七上·朝阳期中)若|x|=5,|y|=2,且xy>0,x<y,则x+y= .
15.如下表,有12个方格,每个方格内都有一个数,若任何相邻三个数的和都是18,则x的值是
﹣5 A B C D E F x G H P 9
16.(2023·海淀模拟)为了鼓励本次模拟练习取得进步的同学,某班决定给该部分同学发放奖品,学习用品商店为了提高营业额,将商品打包促销(每个大礼包限购1个),老师发现了编号分别为,,,,,的六个大礼包中均含有老师需要的一、二、三等奖的奖品,每个大礼包中的各类奖品数量如下:
大礼包编号 一等奖(个) 二等奖(个) 三等奖(个) 总奖品数(个)
1 5 4 10
2 3 3 8
3 1 4 8
4 2 5 11
5 1 3 9
3 4 5 12
该班需要的总的奖品个数不超过41个,且一等奖的个数不少于8个,不超过14个,二等奖的个数不少于7个,不超过13个,且三等奖的个数最多,请同学们帮助老师写出满足条件的购买方案 (写出要购买的大礼包编号)
三、计算题
17.计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)43+(﹣77)+27+(﹣43)
(3)18+(﹣16)+(﹣23)+16
(4)(﹣3)+(+7)+4+3+(﹣5)+(﹣4)
(5)5.6+(﹣0.9)+4.4+(﹣8.1)
(6)(﹣2)+17+(+12)+(﹣4)
18.(2021七上·峄城月考)用适当方法计算:
(1) ;
(2)
(3) ;
(4) .
19.(2022七上·西城月考)年,北京市燃油出租车具体收费标准如下:
①出租车收费标准公里以内收起步价元,再加1元燃油附加费,超过公里,超出部分按每公里元收费;
②预约叫车服务费:提前小时以上预约每次元,小时以内预约每次元;
③单程载客行驶超过公里的部分,按原价时段基本单价(元)加收的费用;
④出租车计价精确到米,超过米但不足米时按米计价,另外,每公里中的米计价元,后米计价按元.
⑤出租车收费结算以元为单位,精确到元(元以下四舍五入).
(注:如果车费不足起步价,则按起步价收费.)
结合以上信息,回答下列问题:
(1)已知肖老师家距离学校公里,周五早上肖老师为了避开早高峰选择时预约出租车出发,一路畅通到达学校,请你计算一下肖老师早上上班的出租车费用是 元;
(2)周五晚上,肖老师预约了周六上午乘出租车去机场,一路畅通到达机场,已知肖老师家距离机场(且为整数)公里,肖老师支付元(包括元高速收费站费用),则y= .
四、解答题
20.(2023七上·桑植期中)某检修小组乘汽车沿公路检修线路,约定往东为正,往西为负.某天自A地出发到收工时所走路线(单位:千米)为:,,,,,,,,,.
(1)问收工时距A地多远?在哪个方向?
(2)若每千米路程耗油m升,问从A地出发到收工共耗油多少升?
21.(2023七上·徐州月考)一辆汽车在一段东西向的公路来回巡查,若规定向东为正,向西为负,行驶的路程(千米)用正负数表示如下:,+4,,+8,,+12,;
(1)这辆车最后离开出发点的哪个方向?离开出发点多远?
(2)这辆车共行驶了多少千米?
22.若|a|=3,|b|=5,且a>b,求a+b的值.
23.(2023七上·惠阳月考)某一出租车一天下午以辰山植物园南门为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+10,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.
(1)将最后一名乘客送到目的地,出租车离出发点多远?在辰山植物园南门的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
答案解析部分
1.【答案】C
【知识点】有理数的加法
2.【答案】B
【知识点】有理数的加法;有理数在数轴上的表示
3.【答案】A
【知识点】有理数的加法法则
4.【答案】C
【知识点】有理数的加法法则
5.【答案】A
【知识点】绝对值的概念与意义;有理数的加法法则
6.【答案】D
【知识点】有理数的加法
7.【答案】D
【知识点】有理数的加法法则
8.【答案】A
【知识点】绝对值的概念与意义;有理数的加法法则
9.【答案】C
【知识点】数轴上两点之间的距离;绝对值的概念与意义;有理数的加法法则
10.【答案】A
【知识点】有理数的加法法则
11.【答案】1
【知识点】化简含绝对值有理数;有理数的加法法则
12.【答案】-2016
【知识点】有理数的加法
13.【答案】
【知识点】绝对值的非负性;有理数的加法法则
14.【答案】-7
【知识点】绝对值及有理数的绝对值;有理数的加法
15.【答案】14
【知识点】有理数的加法
16.【答案】各买一个(答案不唯一)
【知识点】有理数的加法实际应用
17.【答案】(1)解:(﹣3)+40+(﹣32)+(﹣8)
=40+[(﹣3)+(﹣32)+(﹣8)]
=40+(﹣43)
=﹣3
(2)解:43+(﹣77)+27+(﹣43)
=[(43+(﹣43)]+[(﹣77)+27]
=0+(﹣50)
=﹣50
(3)解:18+(﹣16)+(﹣23)+16
=(18+16)+[(﹣16)+(﹣23)]
=34+(﹣39)
=﹣5
(4)解:(﹣3)+(+7)+4+3+(﹣5)+(﹣4)
=[(+7)+4+3]+[(﹣3)+(﹣5)+(﹣4)]
=14+(﹣12)
=2,
(5)解:5.6+(﹣0.9)+4.4+(﹣8.1)
=(5.6+4.4)+[(﹣0.9)+(﹣8.1)]
=10+(﹣9)
=1,
(6)解:
=
=
=
【知识点】有理数的加法法则;有理数的加法运算律
18.【答案】(1)解:原式 ;
(2)解:原式 ;
(3)解:原式
;
(4)解:原式 .
【知识点】有理数的加法
19.【答案】(1)29
(2)
【知识点】有理数的加法法则
20.【答案】(1)解:
=
=-35+37
=2(千米)
答:收工时在正东方向,距离A地2千米.
(2)解:从A地出发到收工行驶的总路程为:
(千米),
∴从A地出发到收工共耗油升.
答:从A地出发到收工共耗油升
【知识点】正数、负数的实际应用;绝对值的概念与意义;有理数的加法实际应用
21.【答案】(1)这辆车最后离开出发点的正西方向,离开出发点10千米
(2)58千米
【知识点】正数、负数的实际应用;有理数的加法实际应用
22.【答案】解:∵|a|=3,|b|=5,且a>b,
∴a=3,b=﹣5;a=﹣3,b=﹣5,
则a+b=﹣2或﹣8
【知识点】相反数及有理数的相反数;有理数的加法
23.【答案】(1)在辰山植物园南门向东1km处;(2)司机一个下午的营业额是141.6元.
【知识点】有理数的加法实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
