四川省甘孜州2024-2025学年八年级下学期期末检测数学试卷(含答案)
文档属性
| 名称 | 四川省甘孜州2024-2025学年八年级下学期期末检测数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 577.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 22:53:41 | ||
图片预览



文档简介
四川省甘孜州2024-2025学年八年级下学期期末检测数学试题
一、单选题
1.下列式子中,最简二次根式是( )
A. B. C. D.
2.某次演讲比赛中,进入决赛的7位同学得分由低到高依次为.这组得分的众数是( ).
A.和 B. C. D.
3.计算的结果是( )
A. B. C. D.
4.通过如下尺规作图,能得到的是( )
A. B.
C. D.
5.已知正多边形的一个外角等于,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9
6.下列从左到右的运算是因式分解,并且分解正确的是( )
A.
B.
C.
D.
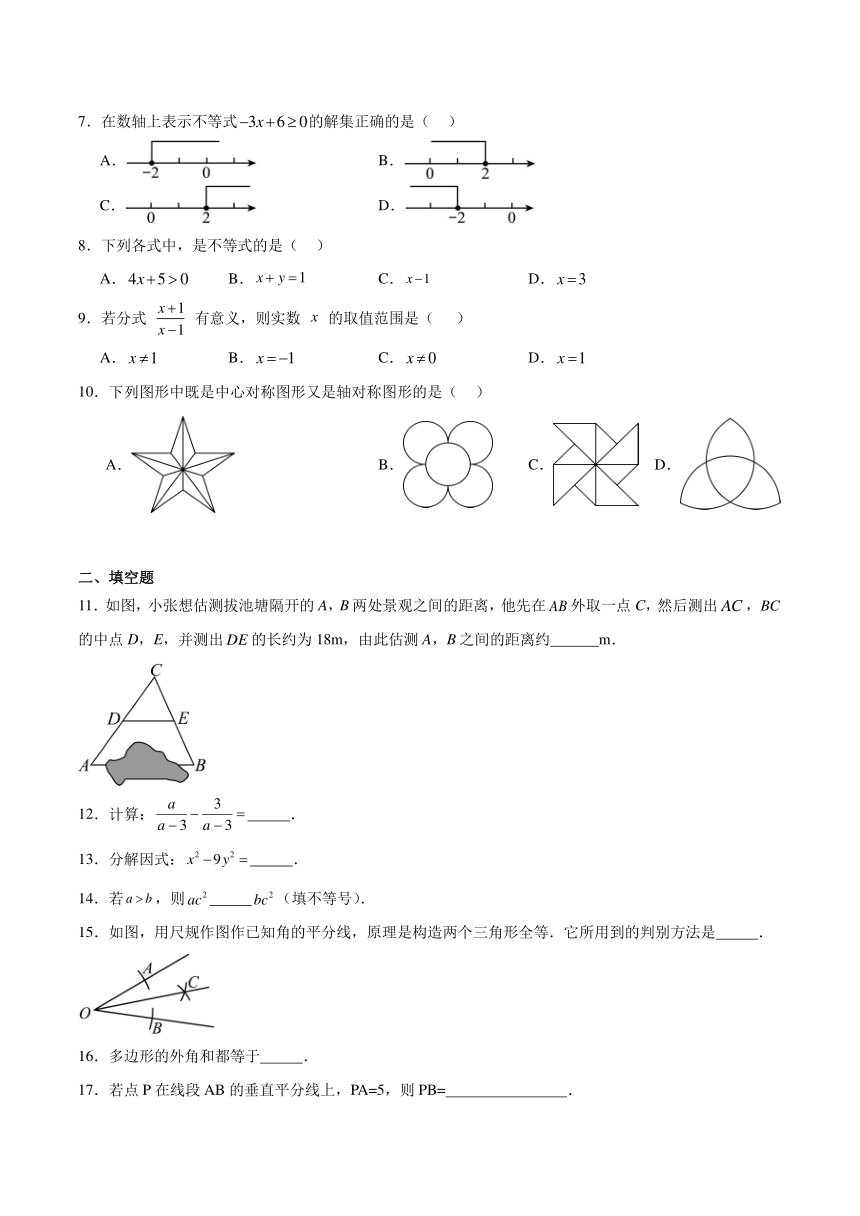
7.在数轴上表示不等式的解集正确的是( )
A. B.
C. D.
8.下列各式中,是不等式的是( )
A. B. C. D.
9.若分式 有意义,则实数 的取值范围是( )
A. B. C. D.
10.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
二、填空题
11.如图,小张想估测拔池塘隔开的A,B两处景观之间的距离,他先在外取一点C,然后测出,的中点D,E,并测出的长约为18m,由此估测A,B之间的距离约 m.
12.计算: .
13.分解因式: .
14.若,则 (填不等号).
15.如图,用尺规作图作已知角的平分线,原理是构造两个三角形全等.它所用到的判别方法是 .
16.多边形的外角和都等于 .
17.若点P在线段AB的垂直平分线上,PA=5,则PB= .
18.用反证法证明“菱形的对角线互相垂直”是真命题时,第一步应先假设 .
19.点在第 象限.
三、解答题
20.计算和解分式方程:
(1)计算:.
(2)解分式方程:.
21.解不等式组请结合题意填空,完成本题的解答.
(1)解不等式①,得_______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为________
22.甲、乙两台机床同时生产一种零件.在10天中,两台机床每天出次品的数量如表.
甲 0 2 1 2 3 2 3 1 2 4
乙 2 3 1 2 0 2 1 3 0 1
(1)通过计算说明哪台机床在10天中生产次品零件的平均数较小?
(2)已知两组数据的方差分别是s甲2=1.2,s乙2=1.14.则生产合格零件比较稳定的机床是 (填“甲”或“乙”).
23.某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,乒乓球赠送.若购买10副直拍球拍和5副横拍球拍花费3250元;购买10副直拍球拍比购买5副横拍球拍多花费750元.求两种球拍每副各多少元?
24.已知:在中,D,E,F分别是边的中点.
求证:四边形的周长等于.
25.如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且ABCD.求证:四边形BECF是平行四边形.
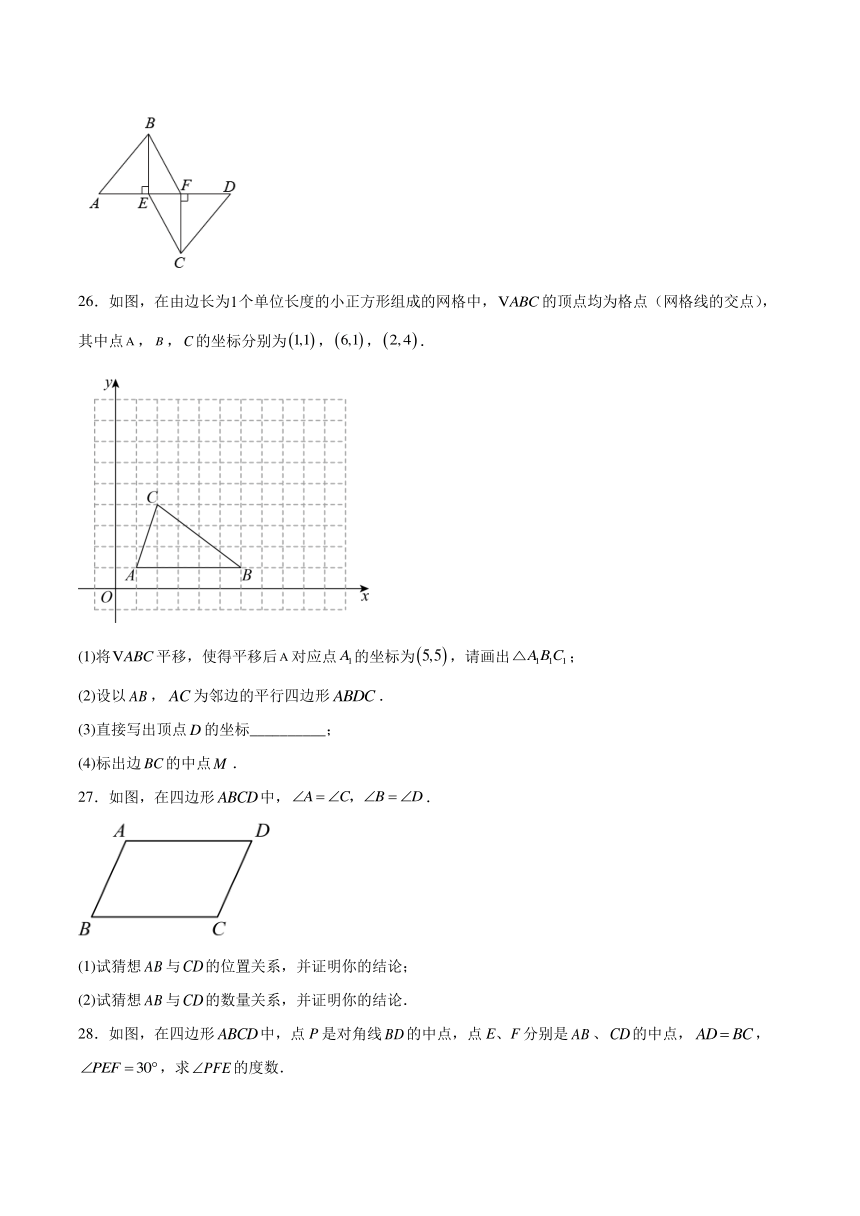
26.如图,在由边长为个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点),其中点,,的坐标分别为,,.
(1)将平移,使得平移后对应点的坐标为,请画出;
(2)设以,为邻边的平行四边形.
(3)直接写出顶点的坐标__________;
(4)标出边的中点.
27.如图,在四边形中,.
(1)试猜想与的位置关系,并证明你的结论;
(2)试猜想与的数量关系,并证明你的结论.
28.如图,在四边形中,点P是对角线的中点,点E、F分别是、的中点,,,求的度数.
参考答案
1.B
解:A、,不是最简二次根式,不符合题意;
B、,是最简二次根式,符合题意;
C、,不是最简二次根式,不符合题意;
D、,不是最简二次根式,不符合题意;
故选B.
2.A
解:这组得分出现次数最多的数是和,
这组得分的众数是和,
故选:A.
3.D
解:
故选:D
4.C
解:当点D在线段的垂直平分线上时,,尺规作图是作线段垂直平分线的是C中的图形.
故选:C.
5.C
正多边形的一个外角等于,且外角和为,
则这个正多边形的边数是:,
故选C.
6.B
解:A. ,不是几个整式乘积的形式,故该选项不符合题意;
B. ,是因式分解,故该选项符合题意;
C. ,故该选项不符合题意;
D. ,故该选项不符合题意;
故选:B.
7.B
解:由得:
解得:
故选:B
8.A
因为是不等式,所以A符合题意;
因为是方程,所以B不符合题意;
因为是代数式,所以C不符合题意;
因为是方程,所以D不符合题意.
故选:A.
9.A
解:∵分式在实数范围内有意义,
∴,
解得,,
故选:A.
10.B
解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.是轴对称图形,是中心对称图形,符合题意;
C.不是轴对称图形,是中心对称图形,不符合题意;
D.是轴对称图形,不是中心对称图形,不符合题意.
故选B.
11.36
∵、分别是、的中点,
∴是的中位线.
∴根据三角形的中位线定理,得.
故答案为: 36 .
12.1
解:,
故答案为:1.
13.
解:
.
故答案为:.
14.
解:,
当时,,
当时,,
,
故答案为:.
15./边边边
解:由作图痕迹得到,,
∵,
∴,
∴,
即平分.
故答案为:.
16./360度
解:多边形的外角和都等于,
故答案为:.
17.5
解析:∵点P在线段AB的垂直平分线上,
∴PB=PA=5.
18.菱形的对角线不互相垂直
解:反证法证明“菱形的对角线互相垂直”是真命题时,第一步应先假设菱形的对角线不互相垂直,
故答案为:菱形的对角线不互相垂直.
19.二
解:点在第二象限.
故答案为:二.
20.(1)
(2)
(1)解:
原式
(2)解:
等式两边同时乘以,得
化简得,
去小括号,得
移项,得
合并同类项,得
系数化为“”,得
经检验,是原方程的解.
21.(1)
(2)
(3)见解析
(4)
(1)解:
移项得,
合并同类项得,,
故答案为:;
(2)解:
移项得,
合并同类项得,,
系数化1得,,
故答案为:;
(3)解:把不等式①和②的解集在数轴上表示出来:
(4)解:原不等式组的解集为,
故答案为:.
22.(1)乙机床在10天中生产次品零件的平均数较小;(2)乙
解:(1)由题意得:,
∵
∴乙机床在10天中生产次品零件的平均数较小;
(2)∵s甲2=1.2,s乙2=1.14,
∴s乙2<s甲2,
∴生产合格零件比较稳定的机床是乙.
23.直拍球拍每副200元,横拍球拍每副250元
解:设设直拍球拍每副x元,横拍球拍每副y元,根据题意得,
,
解得,
答:直拍球拍每副200元,横拍球拍每副250元.
24.见解析
解:如图,
D,E,F分别是边的中点,
、 是 的中位线,
, ,
四边形的周长
,
即四边形的周长等于.
25.见解析
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠BEF=∠CFE=∠CFD=90°,
∴BE∥CF,
∵AB∥CD,
∴∠A=∠D,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF,
∵BE∥CF,
∴四边形BECF是平行四边形.
26.(1)作图见解析
(2)作图见解析
(3)
(4)作图见解析
(1)解:∵将平移,使得平移后对应点的坐标为,
∴向右平移4个单位,再向上平移4个单位后得到,
∵,,
∴,,
连接、、,则即为所作.
(2)∵,,
将线段向右平移1个单位,再向上平移3个单位,点与点对应,
∴点与点对应,
连接,,
∴,,
∴四边形为平行四边形,
则四边形即为所作.
(3)∵,
由(2)可得:将线段向右平移1个单位,再向上平移3个单位,点与点对应,点与点对应,
∴,
故答案为:.
(4)连接交于点,
∵四边形为平行四边形,且与为四边形的对角线,
∴点为的中点,
则点即为所作.
27.(1)
(2)
(1)解:,理由如下:
,
四边形是平行四边形,
.
(2)解:,理由如下:
,
四边形是平行四边形,
.
28.
解:∵在四边形中,P是对角线的中点,E,F分别是、的中点,
∴,分别是与的中位线,
∴,,
∵,
∴,
故是等腰三角形,
∵,
∴.
一、单选题
1.下列式子中,最简二次根式是( )
A. B. C. D.
2.某次演讲比赛中,进入决赛的7位同学得分由低到高依次为.这组得分的众数是( ).
A.和 B. C. D.
3.计算的结果是( )
A. B. C. D.
4.通过如下尺规作图,能得到的是( )
A. B.
C. D.
5.已知正多边形的一个外角等于,那么这个正多边形的边数为( )
A.6 B.7 C.8 D.9
6.下列从左到右的运算是因式分解,并且分解正确的是( )
A.
B.
C.
D.
7.在数轴上表示不等式的解集正确的是( )
A. B.
C. D.
8.下列各式中,是不等式的是( )
A. B. C. D.
9.若分式 有意义,则实数 的取值范围是( )
A. B. C. D.
10.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
二、填空题
11.如图,小张想估测拔池塘隔开的A,B两处景观之间的距离,他先在外取一点C,然后测出,的中点D,E,并测出的长约为18m,由此估测A,B之间的距离约 m.
12.计算: .
13.分解因式: .
14.若,则 (填不等号).
15.如图,用尺规作图作已知角的平分线,原理是构造两个三角形全等.它所用到的判别方法是 .
16.多边形的外角和都等于 .
17.若点P在线段AB的垂直平分线上,PA=5,则PB= .
18.用反证法证明“菱形的对角线互相垂直”是真命题时,第一步应先假设 .
19.点在第 象限.
三、解答题
20.计算和解分式方程:
(1)计算:.
(2)解分式方程:.
21.解不等式组请结合题意填空,完成本题的解答.
(1)解不等式①,得_______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为________
22.甲、乙两台机床同时生产一种零件.在10天中,两台机床每天出次品的数量如表.
甲 0 2 1 2 3 2 3 1 2 4
乙 2 3 1 2 0 2 1 3 0 1
(1)通过计算说明哪台机床在10天中生产次品零件的平均数较小?
(2)已知两组数据的方差分别是s甲2=1.2,s乙2=1.14.则生产合格零件比较稳定的机床是 (填“甲”或“乙”).
23.某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,乒乓球赠送.若购买10副直拍球拍和5副横拍球拍花费3250元;购买10副直拍球拍比购买5副横拍球拍多花费750元.求两种球拍每副各多少元?
24.已知:在中,D,E,F分别是边的中点.
求证:四边形的周长等于.
25.如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且ABCD.求证:四边形BECF是平行四边形.
26.如图,在由边长为个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点),其中点,,的坐标分别为,,.
(1)将平移,使得平移后对应点的坐标为,请画出;
(2)设以,为邻边的平行四边形.
(3)直接写出顶点的坐标__________;
(4)标出边的中点.
27.如图,在四边形中,.
(1)试猜想与的位置关系,并证明你的结论;
(2)试猜想与的数量关系,并证明你的结论.
28.如图,在四边形中,点P是对角线的中点,点E、F分别是、的中点,,,求的度数.
参考答案
1.B
解:A、,不是最简二次根式,不符合题意;
B、,是最简二次根式,符合题意;
C、,不是最简二次根式,不符合题意;
D、,不是最简二次根式,不符合题意;
故选B.
2.A
解:这组得分出现次数最多的数是和,
这组得分的众数是和,
故选:A.
3.D
解:
故选:D
4.C
解:当点D在线段的垂直平分线上时,,尺规作图是作线段垂直平分线的是C中的图形.
故选:C.
5.C
正多边形的一个外角等于,且外角和为,
则这个正多边形的边数是:,
故选C.
6.B
解:A. ,不是几个整式乘积的形式,故该选项不符合题意;
B. ,是因式分解,故该选项符合题意;
C. ,故该选项不符合题意;
D. ,故该选项不符合题意;
故选:B.
7.B
解:由得:
解得:
故选:B
8.A
因为是不等式,所以A符合题意;
因为是方程,所以B不符合题意;
因为是代数式,所以C不符合题意;
因为是方程,所以D不符合题意.
故选:A.
9.A
解:∵分式在实数范围内有意义,
∴,
解得,,
故选:A.
10.B
解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.是轴对称图形,是中心对称图形,符合题意;
C.不是轴对称图形,是中心对称图形,不符合题意;
D.是轴对称图形,不是中心对称图形,不符合题意.
故选B.
11.36
∵、分别是、的中点,
∴是的中位线.
∴根据三角形的中位线定理,得.
故答案为: 36 .
12.1
解:,
故答案为:1.
13.
解:
.
故答案为:.
14.
解:,
当时,,
当时,,
,
故答案为:.
15./边边边
解:由作图痕迹得到,,
∵,
∴,
∴,
即平分.
故答案为:.
16./360度
解:多边形的外角和都等于,
故答案为:.
17.5
解析:∵点P在线段AB的垂直平分线上,
∴PB=PA=5.
18.菱形的对角线不互相垂直
解:反证法证明“菱形的对角线互相垂直”是真命题时,第一步应先假设菱形的对角线不互相垂直,
故答案为:菱形的对角线不互相垂直.
19.二
解:点在第二象限.
故答案为:二.
20.(1)
(2)
(1)解:
原式
(2)解:
等式两边同时乘以,得
化简得,
去小括号,得
移项,得
合并同类项,得
系数化为“”,得
经检验,是原方程的解.
21.(1)
(2)
(3)见解析
(4)
(1)解:
移项得,
合并同类项得,,
故答案为:;
(2)解:
移项得,
合并同类项得,,
系数化1得,,
故答案为:;
(3)解:把不等式①和②的解集在数轴上表示出来:
(4)解:原不等式组的解集为,
故答案为:.
22.(1)乙机床在10天中生产次品零件的平均数较小;(2)乙
解:(1)由题意得:,
∵
∴乙机床在10天中生产次品零件的平均数较小;
(2)∵s甲2=1.2,s乙2=1.14,
∴s乙2<s甲2,
∴生产合格零件比较稳定的机床是乙.
23.直拍球拍每副200元,横拍球拍每副250元
解:设设直拍球拍每副x元,横拍球拍每副y元,根据题意得,
,
解得,
答:直拍球拍每副200元,横拍球拍每副250元.
24.见解析
解:如图,
D,E,F分别是边的中点,
、 是 的中位线,
, ,
四边形的周长
,
即四边形的周长等于.
25.见解析
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠BEF=∠CFE=∠CFD=90°,
∴BE∥CF,
∵AB∥CD,
∴∠A=∠D,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF,
∵BE∥CF,
∴四边形BECF是平行四边形.
26.(1)作图见解析
(2)作图见解析
(3)
(4)作图见解析
(1)解:∵将平移,使得平移后对应点的坐标为,
∴向右平移4个单位,再向上平移4个单位后得到,
∵,,
∴,,
连接、、,则即为所作.
(2)∵,,
将线段向右平移1个单位,再向上平移3个单位,点与点对应,
∴点与点对应,
连接,,
∴,,
∴四边形为平行四边形,
则四边形即为所作.
(3)∵,
由(2)可得:将线段向右平移1个单位,再向上平移3个单位,点与点对应,点与点对应,
∴,
故答案为:.
(4)连接交于点,
∵四边形为平行四边形,且与为四边形的对角线,
∴点为的中点,
则点即为所作.
27.(1)
(2)
(1)解:,理由如下:
,
四边形是平行四边形,
.
(2)解:,理由如下:
,
四边形是平行四边形,
.
28.
解:∵在四边形中,P是对角线的中点,E,F分别是、的中点,
∴,分别是与的中位线,
∴,,
∵,
∴,
故是等腰三角形,
∵,
∴.
同课章节目录
