四川省甘孜州2024-2025学年七年级下学期期末检测数学试卷(含答案)
文档属性
| 名称 | 四川省甘孜州2024-2025学年七年级下学期期末检测数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 22:11:36 | ||
图片预览



文档简介
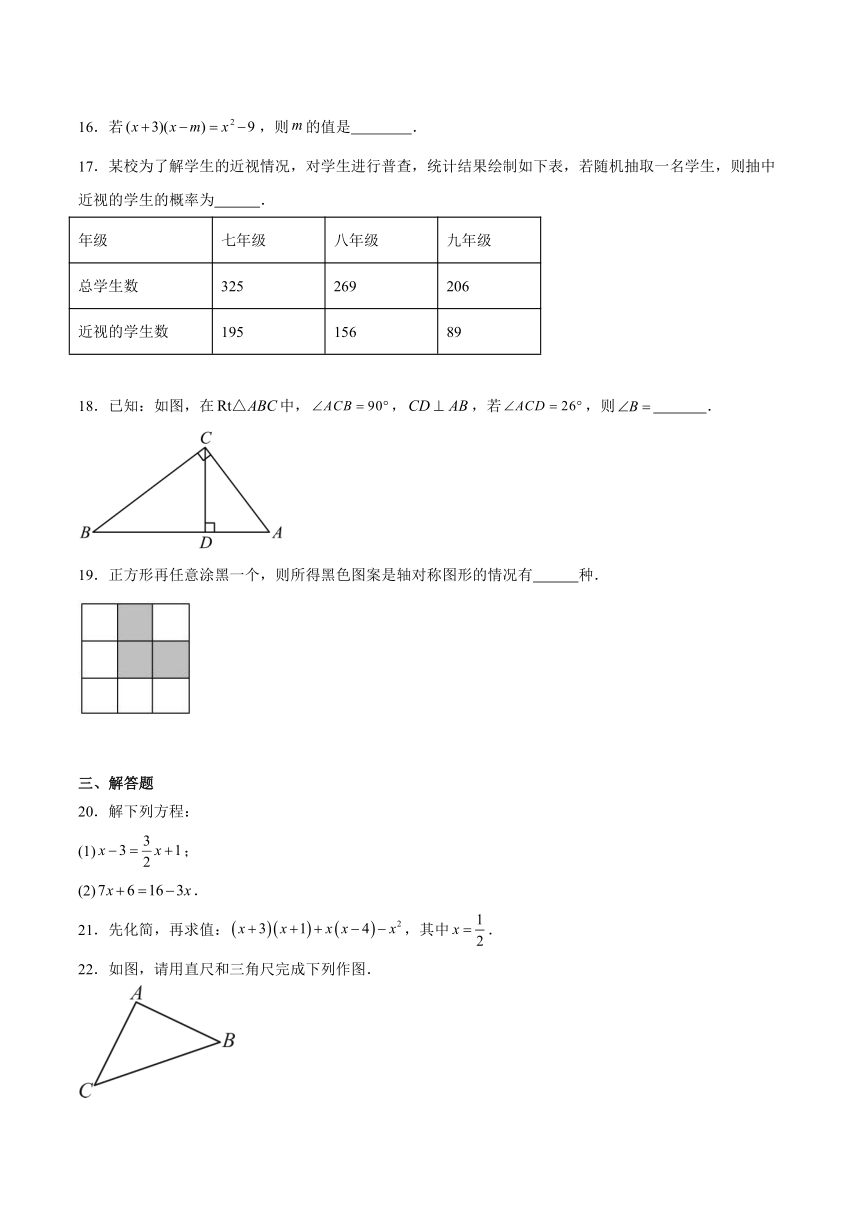
四川省甘孜州2024-2025学年七年级下学期期末检测数学试卷
一、单选题
1.下列各数中,最小的数是( )
A. B. C.0 D.1
2.2024年7月26日巴黎奥运会开幕,吸引了无数观众的目光.根据新华社报道,约32万名观众在雨中观看了开幕式.此次开幕式是历史上首次不在体育场内举办,而是在塞纳河上进行.数据“32万”用科学记数法表示为( )
A. B. C. D.
3.下面给出的图形中,绕虚线旋转一周能形成圆柱的是( )
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.化简的结果为( )
A. B. C. D.
6.在同一平面内,两条直线可能的位置关系是 ( )
A.平行 B.相交 C.相交或平行 D.相交、平行或垂直
7.下列成语描述的事件中,发生的可能性最小的是( )
A.守株待兔 B.瓮中捉鳖 C.顺藤摸瓜 D.日落西山
8.在掷一枚骰子次的试验中,“偶数朝上”的频数为,则“偶数朝上”的频率为( )
A. B. C. D.
9.下列长度的三条线段能组成三角形的是( )
A.,, B.,,
C.,, D.,,
10.窗花在中国的传统节日中扮演着重要的角色,如图是同学们设计的窗花作品,其中为轴对称图形的是( )
A. B. C. D.
二、填空题
11. .
12.若与是同类项,则 .
13.一个角的余角是,则这个角的度数为 .
14.如图,一只蚂蚁从电线杆的顶端爬到地面上,它能爬行的路线有和两条,已知,则路线最短,原因是 .
15.计算的结果是 .
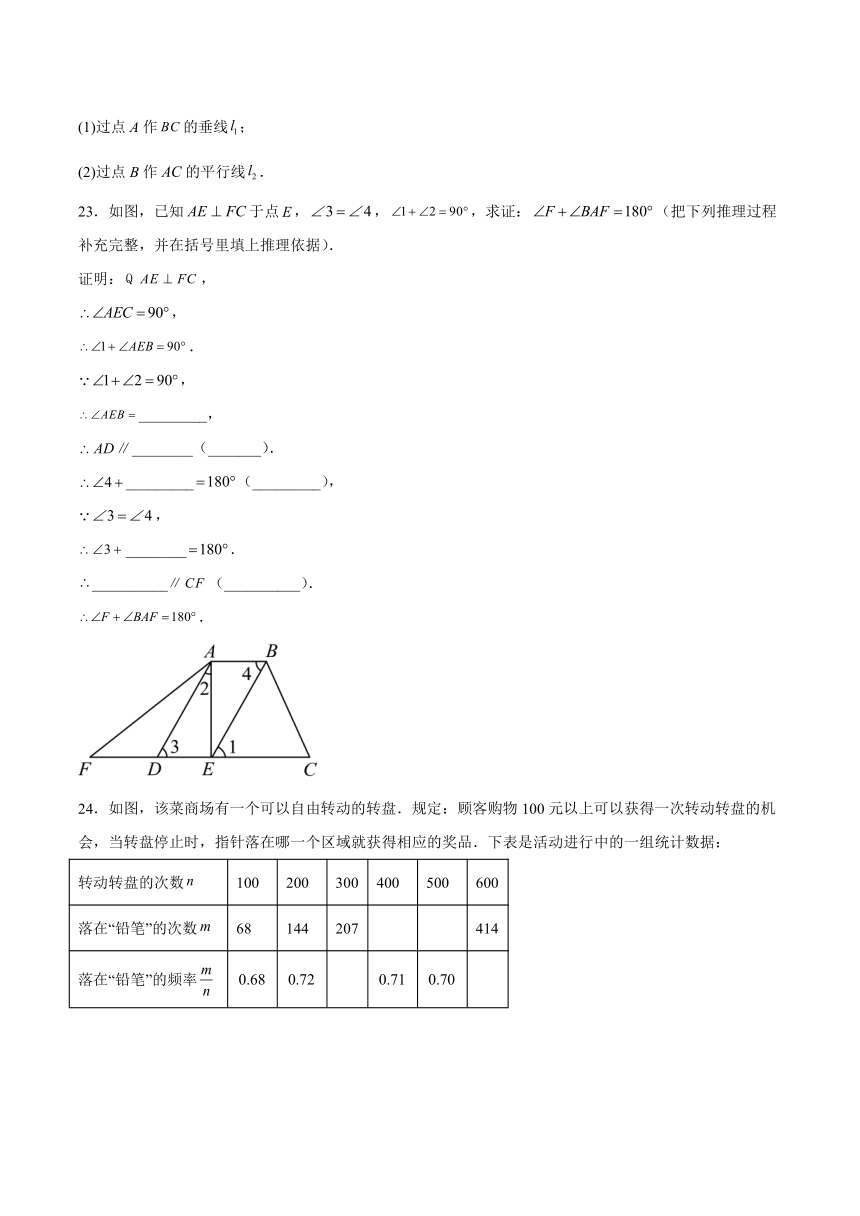
16.若,则的值是 .
17.某校为了解学生的近视情况,对学生进行普查,统计结果绘制如下表,若随机抽取一名学生,则抽中近视的学生的概率为 .
年级 七年级 八年级 九年级
总学生数 325 269 206
近视的学生数 195 156 89
18.已知:如图,在中,,,若,则 .
19.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
三、解答题
20.解下列方程:
(1);
(2).
21.先化简,再求值:,其中.
22.如图,请用直尺和三角尺完成下列作图.
(1)过点A作的垂线;
(2)过点B作的平行线.
23.如图,已知于点,,,求证:(把下列推理过程补充完整,并在括号里填上推理依据).
证明:,
,
.
,
_________,
________(_______).
_________(_________),
,
________.
__________(__________).
.
24.如图,该菜商场有一个可以自由转动的转盘.规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 100 200 300 400 500 600
落在“铅笔”的次数 68 144 207 414
落在“铅笔”的频率
(1)计算并完成表格;
(2)转动该转盘一次,获得铅笔的概率约是___________.(结果保留小数点后一位)
25.如图,A、B、C为网格图中的三点,利用网格作图.
(1)过点A画直线AD∥BC;
(2)过点A画线段BC的垂线AH,垂足为H;
(3)点A到直线BC的距离是线段 的长;
(4)三角形ABC的面积为 .
26.为保护学生的视力,课桌椅的高度均按一定的关系配套设计已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可近似地表示为,其中y表示课桌的高度(单位:),x表示椅子的高度(单位:).
(1)求当椅子的高度为时,课桌的高度.
(2)求当课桌的高度为时,椅子的高度.
27.开封风筝是河南开封地区传统民间工艺品.开封风筝历史悠久、种类繁多、做工精细、独具特色.每年农历正月至三月的庙会上,各式各样的风箏竞相牵放,景象十分壮观.图1是小华制作的风筝,图2是风筝骨架的示意图,其中,.
(1)求证:;
(2)小华发现平分,你觉得他的发现正确吗?请说明理由.
28.如图,已知,,.
(1)求证:;
(2)求的度数.
参考答案
1.B
解:,
∴最小的数是:.
故选:B.
2.D
解:32万,
故选:D.
3.D
解:绕虚线旋转一周能形成圆柱的是:
,
故选D.
4.A
解:A、,原式计算正确,符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算错误,不符合题意;
D、,原式计算错误,不符合题意;
故选:A.
5.B
解:,
故选:B.
6.C
解:在同一平面内,两条直线可能的位置关系是相交或平行,
故选:C.
7.A
解:A、守株待兔是极小概率事件,本选项符合题意;
B、瓮中捉鳖是必然事件,本选项不符合题意;
C、顺藤摸瓜是必然事件,本选项不符合题意;
D、日落西山是必然事件,本选项不符合题意;
故选:A.
8.C
解:由题意得:
,
“偶数朝上”的频率为,
故选:C.
9.A
解:选项A:最长边为,较短两边之和为,,满足三角形三边关系,能组成三角形.
选项B:最长边为,较短两边之和为,,不满足条件,不能组成三角形.
选项C:最长边为,较短两边之和为,,不满足“两边之和大于第三边”,不能组成三角形.
选项D:最长边为,较短两边之和为.,同样不满足条件,不能组成三角形.
故选:A
10.A
解:选项A的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
选项B、C、D的图形不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
故选:A.
11.2
解:.
故答案为:2.
12.
解:∵与是同类项,
∴
故答案为:3.
13./83度
解:由题意得:这个角的度数为,
故答案为:
14.垂线段最短
解:由题意,路线最短,原因是垂线段最短;
故答案为:垂线段最短
15.
解∶
故答案为∶
16.3
解:,
,
,
故答案为:3.
17.
解:抽中近视的学生的概率是: ,
故答案为:
18./26度
解:,,
,
,
,
.
故答案为:.
19.4
解:如图所示:
,
共4种,
故答案为:4.
20.(1)
(2)
解:(1)
移项,得.
合并同类项,得.
系数化为1,得;
(2)
移项,得.
合并同类项,得.
系数化为1,得.
21.,
解:原式 =
当 时,原式
22.(1)见解析
(2)见解析
(1)
过点A作的垂线:
步骤1:确定三角板的位置.将三角板的一条直角边与直线对齐,同时确保三角板的另一条直角边通过点A.
步骤2:画出垂线.沿三角板的直角边从点A画出一条直线,这条直线即为过点A的的垂线.
(2)见(1)图
过点B作的平行线:
步骤1:确定三角板的位置.将三角板的一条直角边与直线对齐,同时确保三角板的另一条直角边通过点B.
步骤2:移动三角板,使其保持与平行的状态.使用直尺辅助,将三角板沿着直线的方向移动,直至三角板的某一边通过点B.
步骤3:画出平行线.沿三角板的直角边从点B画出一条直线,这条直线即为过点B的的平行线.
23.;;内错角相等,两直线平行;;两直线平行,同旁内角互补;;;同旁内角互补,两直线平行
证明:,
,
.
,
,
(内错角相等,两直线平行).
(两直线平行,同旁内角互补),
,
.
(同旁内角互补,两直线平行).
.
故答案为:;;内错角相等,两直线平行;;两直线平行,同旁内角互补;;;同旁内角互补,两直线平行.
24.(1)见解析
(2)
(1)解:当,时,;
当,时,;
当,时,;
当,时,;
完成表格如下:
转动转盘的次数 100 200 300 400 500 600
落在“铅笔”的次数 68 144 207 284 350 414
落在“铅笔”的频率
(2)解:由表格得,落在“铅笔”的频率稳定在附近,
转动该转盘一次,获得铅笔的概率约是.
25.(1)见解析
(2)见解析
(3)AH
(4)2.5
(1)解:如图,取格点D,作直线AD,直线AD即为所求;
(2)解:如图, 取格点E,作直线AE交BC于点H,直线AH即为所求;
(3)解:点A到直线BC的距离是线段AH的长;
故答案为:AH;
(4)解:三角形ABC的面积=2×3﹣×1×2﹣×1×2﹣×1×3=2.5.
故答案为:2.5.
26.(1)
(2)
(1)解:当时,.
答:当椅子的高度为时,课桌的高度为.
(2)当时,,
解得.
答:当课桌的高度为时,椅子的高度为.
27.(1)见解析
(2)正确,见解析
【分析】此题考查了全等三角形的判定与性质;
(1)利用即可证明;
(2)根据全等三角形的性质及角平分线定义求解即可.
【详解】(1)证明:在和中,
,
∴;
(2)解:正确,理由:
由(1)得,
∴,
即平分,
所以小华的发现是正确的.
28.(1)证明过程见详解
(2)
(1)证明:,,
,
在和中
,
;
(2)解:,
,
.
一、单选题
1.下列各数中,最小的数是( )
A. B. C.0 D.1
2.2024年7月26日巴黎奥运会开幕,吸引了无数观众的目光.根据新华社报道,约32万名观众在雨中观看了开幕式.此次开幕式是历史上首次不在体育场内举办,而是在塞纳河上进行.数据“32万”用科学记数法表示为( )
A. B. C. D.
3.下面给出的图形中,绕虚线旋转一周能形成圆柱的是( )
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.化简的结果为( )
A. B. C. D.
6.在同一平面内,两条直线可能的位置关系是 ( )
A.平行 B.相交 C.相交或平行 D.相交、平行或垂直
7.下列成语描述的事件中,发生的可能性最小的是( )
A.守株待兔 B.瓮中捉鳖 C.顺藤摸瓜 D.日落西山
8.在掷一枚骰子次的试验中,“偶数朝上”的频数为,则“偶数朝上”的频率为( )
A. B. C. D.
9.下列长度的三条线段能组成三角形的是( )
A.,, B.,,
C.,, D.,,
10.窗花在中国的传统节日中扮演着重要的角色,如图是同学们设计的窗花作品,其中为轴对称图形的是( )
A. B. C. D.
二、填空题
11. .
12.若与是同类项,则 .
13.一个角的余角是,则这个角的度数为 .
14.如图,一只蚂蚁从电线杆的顶端爬到地面上,它能爬行的路线有和两条,已知,则路线最短,原因是 .
15.计算的结果是 .
16.若,则的值是 .
17.某校为了解学生的近视情况,对学生进行普查,统计结果绘制如下表,若随机抽取一名学生,则抽中近视的学生的概率为 .
年级 七年级 八年级 九年级
总学生数 325 269 206
近视的学生数 195 156 89
18.已知:如图,在中,,,若,则 .
19.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
三、解答题
20.解下列方程:
(1);
(2).
21.先化简,再求值:,其中.
22.如图,请用直尺和三角尺完成下列作图.
(1)过点A作的垂线;
(2)过点B作的平行线.
23.如图,已知于点,,,求证:(把下列推理过程补充完整,并在括号里填上推理依据).
证明:,
,
.
,
_________,
________(_______).
_________(_________),
,
________.
__________(__________).
.
24.如图,该菜商场有一个可以自由转动的转盘.规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 100 200 300 400 500 600
落在“铅笔”的次数 68 144 207 414
落在“铅笔”的频率
(1)计算并完成表格;
(2)转动该转盘一次,获得铅笔的概率约是___________.(结果保留小数点后一位)
25.如图,A、B、C为网格图中的三点,利用网格作图.
(1)过点A画直线AD∥BC;
(2)过点A画线段BC的垂线AH,垂足为H;
(3)点A到直线BC的距离是线段 的长;
(4)三角形ABC的面积为 .
26.为保护学生的视力,课桌椅的高度均按一定的关系配套设计已知课桌的高度随着椅子的高度变化而变化,它们之间的关系可近似地表示为,其中y表示课桌的高度(单位:),x表示椅子的高度(单位:).
(1)求当椅子的高度为时,课桌的高度.
(2)求当课桌的高度为时,椅子的高度.
27.开封风筝是河南开封地区传统民间工艺品.开封风筝历史悠久、种类繁多、做工精细、独具特色.每年农历正月至三月的庙会上,各式各样的风箏竞相牵放,景象十分壮观.图1是小华制作的风筝,图2是风筝骨架的示意图,其中,.
(1)求证:;
(2)小华发现平分,你觉得他的发现正确吗?请说明理由.
28.如图,已知,,.
(1)求证:;
(2)求的度数.
参考答案
1.B
解:,
∴最小的数是:.
故选:B.
2.D
解:32万,
故选:D.
3.D
解:绕虚线旋转一周能形成圆柱的是:
,
故选D.
4.A
解:A、,原式计算正确,符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算错误,不符合题意;
D、,原式计算错误,不符合题意;
故选:A.
5.B
解:,
故选:B.
6.C
解:在同一平面内,两条直线可能的位置关系是相交或平行,
故选:C.
7.A
解:A、守株待兔是极小概率事件,本选项符合题意;
B、瓮中捉鳖是必然事件,本选项不符合题意;
C、顺藤摸瓜是必然事件,本选项不符合题意;
D、日落西山是必然事件,本选项不符合题意;
故选:A.
8.C
解:由题意得:
,
“偶数朝上”的频率为,
故选:C.
9.A
解:选项A:最长边为,较短两边之和为,,满足三角形三边关系,能组成三角形.
选项B:最长边为,较短两边之和为,,不满足条件,不能组成三角形.
选项C:最长边为,较短两边之和为,,不满足“两边之和大于第三边”,不能组成三角形.
选项D:最长边为,较短两边之和为.,同样不满足条件,不能组成三角形.
故选:A
10.A
解:选项A的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
选项B、C、D的图形不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
故选:A.
11.2
解:.
故答案为:2.
12.
解:∵与是同类项,
∴
故答案为:3.
13./83度
解:由题意得:这个角的度数为,
故答案为:
14.垂线段最短
解:由题意,路线最短,原因是垂线段最短;
故答案为:垂线段最短
15.
解∶
故答案为∶
16.3
解:,
,
,
故答案为:3.
17.
解:抽中近视的学生的概率是: ,
故答案为:
18./26度
解:,,
,
,
,
.
故答案为:.
19.4
解:如图所示:
,
共4种,
故答案为:4.
20.(1)
(2)
解:(1)
移项,得.
合并同类项,得.
系数化为1,得;
(2)
移项,得.
合并同类项,得.
系数化为1,得.
21.,
解:原式 =
当 时,原式
22.(1)见解析
(2)见解析
(1)
过点A作的垂线:
步骤1:确定三角板的位置.将三角板的一条直角边与直线对齐,同时确保三角板的另一条直角边通过点A.
步骤2:画出垂线.沿三角板的直角边从点A画出一条直线,这条直线即为过点A的的垂线.
(2)见(1)图
过点B作的平行线:
步骤1:确定三角板的位置.将三角板的一条直角边与直线对齐,同时确保三角板的另一条直角边通过点B.
步骤2:移动三角板,使其保持与平行的状态.使用直尺辅助,将三角板沿着直线的方向移动,直至三角板的某一边通过点B.
步骤3:画出平行线.沿三角板的直角边从点B画出一条直线,这条直线即为过点B的的平行线.
23.;;内错角相等,两直线平行;;两直线平行,同旁内角互补;;;同旁内角互补,两直线平行
证明:,
,
.
,
,
(内错角相等,两直线平行).
(两直线平行,同旁内角互补),
,
.
(同旁内角互补,两直线平行).
.
故答案为:;;内错角相等,两直线平行;;两直线平行,同旁内角互补;;;同旁内角互补,两直线平行.
24.(1)见解析
(2)
(1)解:当,时,;
当,时,;
当,时,;
当,时,;
完成表格如下:
转动转盘的次数 100 200 300 400 500 600
落在“铅笔”的次数 68 144 207 284 350 414
落在“铅笔”的频率
(2)解:由表格得,落在“铅笔”的频率稳定在附近,
转动该转盘一次,获得铅笔的概率约是.
25.(1)见解析
(2)见解析
(3)AH
(4)2.5
(1)解:如图,取格点D,作直线AD,直线AD即为所求;
(2)解:如图, 取格点E,作直线AE交BC于点H,直线AH即为所求;
(3)解:点A到直线BC的距离是线段AH的长;
故答案为:AH;
(4)解:三角形ABC的面积=2×3﹣×1×2﹣×1×2﹣×1×3=2.5.
故答案为:2.5.
26.(1)
(2)
(1)解:当时,.
答:当椅子的高度为时,课桌的高度为.
(2)当时,,
解得.
答:当课桌的高度为时,椅子的高度为.
27.(1)见解析
(2)正确,见解析
【分析】此题考查了全等三角形的判定与性质;
(1)利用即可证明;
(2)根据全等三角形的性质及角平分线定义求解即可.
【详解】(1)证明:在和中,
,
∴;
(2)解:正确,理由:
由(1)得,
∴,
即平分,
所以小华的发现是正确的.
28.(1)证明过程见详解
(2)
(1)证明:,,
,
在和中
,
;
(2)解:,
,
.
同课章节目录
