河北省保定市安新县2024-2025学年七年级下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 河北省保定市安新县2024-2025学年七年级下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 22:56:24 | ||
图片预览



文档简介
河北省保定市安新县2024-2025学年七年级下学期期末考试数学试题
一、单选题
1.如图,在平面内过点作已知直线的平行线,可作的条数为( )
A.1 B.2 C.3 D.无数条
2.若,且,则的值可能是( )
A. B.0 C.1 D.4
3.下列各项调查适合全面调查的是( )
A.白洋淀中现有鱼的种类 B.某班每位同学的视力情况
C.某品牌节能灯的使用寿命 D.了解某市观众对《哪吒2》的观影感受
4.如图,淇淇从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用表示,那么表示的位置是( )
A.点A B.点B C.点C D.点D
5.甲、乙两人求二元一次方程的整数解,甲正确地求出一组解为,乙把看成,求得一组解为,则a,b的值为( )
A. B. C. D.
6.已知点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.下列说法正确的是( )
A.的立方根是 B.的平方根是
C.的算术平方根是3 D.1的平方根是1
8.如图,分别平分与,且.证明.下面是不完整的推理过程,
证明:分别平分与(已知),
___________(角平分线的定义),
(已知),
_________(等量代换),
(已知),
_________,
.
下列说法错误的是( )
A.☆表示 B.表示
C.表示 D.表示内错角相等,两直线平行
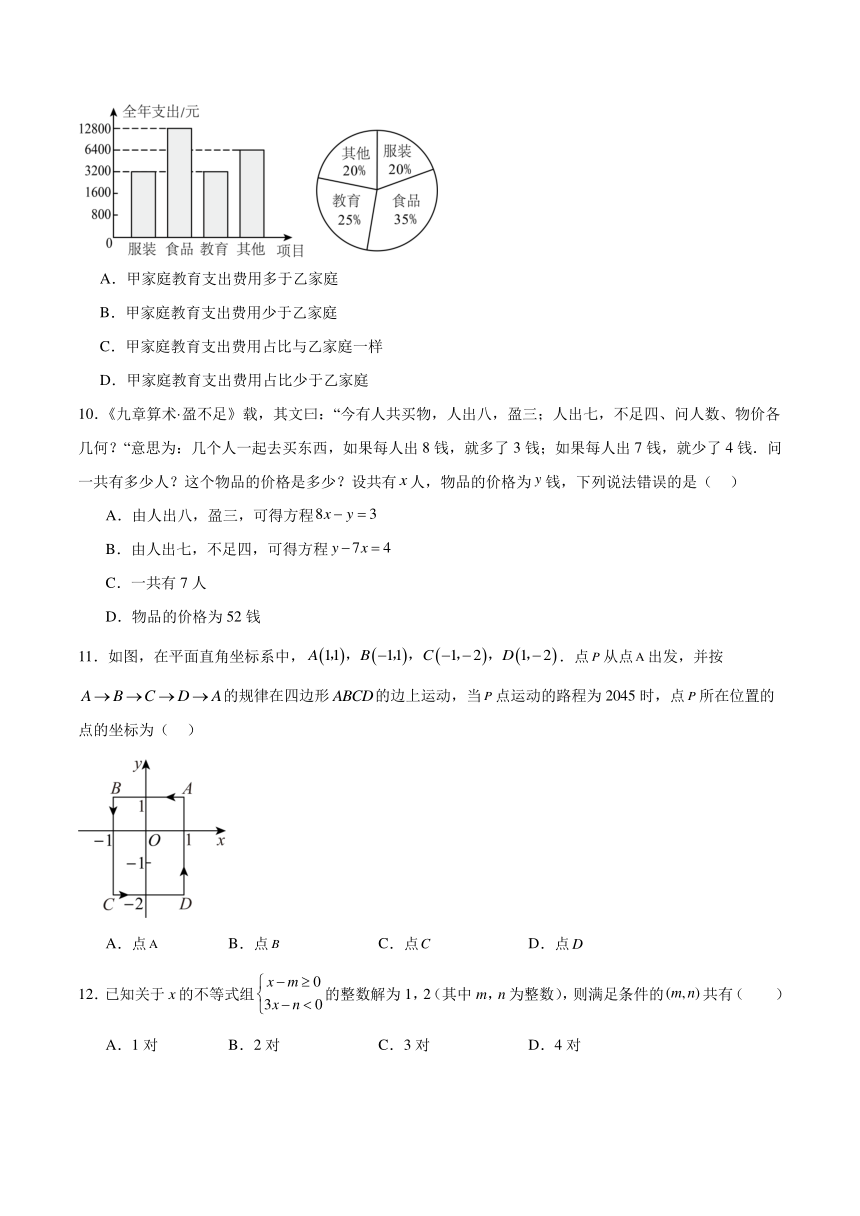
9.如图条形统计图、扇形统计图分别是甲、乙两家庭全年支出费用的统计图.根据统计图,对两家庭教育支出费用所作出的判断中,一定正确的是( )
A.甲家庭教育支出费用多于乙家庭
B.甲家庭教育支出费用少于乙家庭
C.甲家庭教育支出费用占比与乙家庭一样
D.甲家庭教育支出费用占比少于乙家庭
10.《九章算术·盈不足》载,其文曰:“今有人共买物,人出八,盈三;人出七,不足四、问人数、物价各几何?“意思为:几个人一起去买东西,如果每人出8钱,就多了3钱;如果每人出7钱,就少了4钱.问一共有多少人?这个物品的价格是多少?设共有人,物品的价格为钱,下列说法错误的是( )
A.由人出八,盈三,可得方程
B.由人出七,不足四,可得方程
C.一共有7人
D.物品的价格为52钱
11.如图,在平面直角坐标系中,.点从点出发,并按的规律在四边形的边上运动,当点运动的路程为2045时,点所在位置的点的坐标为( )
A.点 B.点 C.点 D.点
12.已知关于x的不等式组的整数解为1,2(其中m,n为整数),则满足条件的共有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
13.通常来说,在一定范围内,销售单价越高,月销售量越低,下表记录了某文具的销售单价和月销售量的数据,请你根据月销售量与销售单价的变化趋势,预测当销售单价为16元/个时,月销售量约为 个.
销售单价(元) ... 10 11 12 13 14 ...
月销售量(个) ... 160 149 140 130 120 ...
14.设为正整数,且,则的值为 .
15.如图,直线b、c被直线a所截,如果,,那么与其内错角的角度之和等于 .
16.如图,一个容量为的杯子中装有的水,先将6颗相同的小玻璃球放入这个杯中后,总体积变为,接着依次放入4个相同的小铁块,直到放入第4个后,发现有水溢出.若每个小玻璃球的体积是,每个小铁块的体积是,则下列说法:①;②;③杯子中仅放小铁块,依次放入,放到第8个,水就会溢出;④若杯子中仅放小玻璃球,至少放11个,水才会溢出,正确的是 .(填序号)
三、解答题
17.解不等式组并把解集表示在数轴上.
18.如图,已知,射线交于点,交于点,从点引一条射线,且.
(1)求证:;
(2)若命题“已知___________,则”是真命题,请填空,并说明理由.
19.为了解某校七年级学生一分钟标准仰卧起坐情况,对该校全部七年级学生进行一分钟标准仰卧起坐个数的测试,并把测得数据分成四组,绘制成如下不完整的频数分布表和频数分布直方图(每一组不含前一个边界值,含后一个边界值).已知一分钟标准仰卧起坐个数在“”的人数占七年级总人数的
组别(个) 频数
48
96
a
72
(1)求七年级的学生总人数及a的值;
(2)把频数分布直方图补充完整;
(3)若一分钟标准仰卧起坐在30个以上为合格,求该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比
20.有一个数学游戏,如图有三种运算,每一种运算都是在上一步运算后进行的一步运算.将3按的顺序运算,即.
(1)将按的顺序运算,写出运算过程并求出结果;
(2)若小于的数按的顺序运算,结果总是大于5,请验证这个结论.
21.如图,一只蚂蚁从点沿数轴向右爬行2个单位长度到达点,点表示的数为,设表示的数为.
(1)求的立方根;
(2)求的值.
22.某校八年级660名学生到郊外参加研学活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用2辆小客车和3辆大客车每次可运送学生175人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,恰好每辆车都坐满且两种车都要租,请你设计出所有的租车方案.
23.在平面直角坐标系中,对于点,若点B的坐标为,则称点为点的“级关联点”,如点的“级关联点”点B的坐标为,即
(1)已知点的“级关联点”为,求点的坐标,并写出点到轴的距离;
(2)已知点的“级关联点”为,求点的坐标及所在象限;
(3)如果点的“级关联点”在轴上,求点的坐标.
24.【问题背景】
直线相交于点在的逆时针方向),的平分线在直线上.
(1)【数学理解】
如图1,平分.
①若,求的度数;
②若,请直接写出的度数(用含的代数式表示).
(2)【构建联系】
如图2,平分,若,求的度数(用含的代数式表示).
(3)【总结应用】
若,请直接写出的度数.
参考答案
1.A
解:根据经过经过直线外一点有且只有一条直线与已知直线平行,
故选:A.
2.A
,且,
,
∴的值可能是.
故选:A.
3.B
解: 选项A:白洋淀鱼种类多、分布广,全面调查难度大,适合抽样调查;
选项B:某班学生人数有限,逐一检查视力可行且需精确数据,适合全面调查;
选项C:测试节能灯寿命需破坏性实验,无法普查,适合抽样调查;
选项D:某市观众数量庞大,全面调查成本过高,适合抽样调查;
综上,仅选项B符合全面调查条件;
故选:B
4.B
解:根据先向东走15米,再向北走10米到达点M,且点M的位置用表示,
横坐标用了3个单位长度表示,得到一个单位长度表示5米,
则的横坐标的绝对值为一个单位长度,纵坐标的绝对值是2个单位长度,
故选:B.
5.C
解:由题意可得,
,
解得,
故选C.
6.C
解:∵点在第四象限,
∴,
解得:,
在数轴上表示为:
故选:C.
7.C
解:A. 错误,的立方根是,而非,
B. 错误,,其平方根为,而非,
C. 正确,,其算术平方根为;
D. 错误,1的平方根是,而非仅1;
故选:C
8.C
解:分别平分与(已知),
,A不符合题意;
(已知),
,B不符合题意;
(已知),
,C符合题意;
(内错角相等,两直线平行),D不符合题意;
故选:C
9.D
解:甲家庭教育支出费用占比为;
∵乙家庭教育支出费用占比为,
∴甲家庭教育支出费用占比少于乙家庭,
由于不确定乙家庭支出的总费用,故无法比较甲家庭教育支出费用和乙家庭教育支出费用的多少,
故选D.
10.D
解:设共有人,物价为钱,
根据“每人出8钱,盈3钱”得方程:(选项A正确);
根据“每人出7钱,不足4钱”得方程:(选项B正确);
联立方程组:,
解得:,
因此共有7人(选项C正确);物价为53钱,而选项D中物价为52钱,错误;
故选:D
11.C
解:,,,,
,,
,
点从点出发,并按的规律在四边形的边上运动,
当点运动的路程为2045时,
,
经历次循环,且走5个单位长度,
点所在位置的点的坐标为,即为点;
故选:C.
12.C
解:解不等式得,
;
解不等式得,
;
因为不等式组的整数解为1,2,
所以,且,
则,.
又因为,为整数,
所以,,8,9,
所以满足条件的共有3对.
故选:C
13.100
解:由表可知:售价每增加1元,月销量约减少10个,
∴当销售单价为16元/个时,月销售量比销售单价为14元/个时约减少20个,即约为100个;
故答案为:100.
14.3
解:∵,
∴,
∵,
∴.
故答案为:3.
15./度
解:,
的内错角为,
,
,
与其内错角的角度之和为,
故答案为:.
16.①②④
解:由装有的水,先将6颗相同的小玻璃球放入这个杯中后,总体积变为,得,则①正确;
体积由变为,接着依次放入4个相同的小铁块,直到放入第4个后,发现有水溢出,得,
解得,则②正确;
杯子中仅放小铁块,,
取,,
所以放入8个小铁块,水不一定溢出,则③不正确;
若杯子中仅放小玻璃球,设可以放个,杯子的水会溢出,
则,解得,则④正确.
故答案为:①②④.
17.,数轴上表示见解析
解:解不等式①得,;
解不等式②得,,
所以不等式组的解集为,其解集在数轴上表示如图所示.
.
18.(1)见解析
(2);理由见解析
(1)证明:∵,,,
∴,
∴;
(2)解:,则;
理由:∵,
∴,
∵,
∴,
∵,
∴.
19.(1)七年级的学生总人数为360人,a的值为144
(2)见解析
(3)
(1)解:已知一分钟标准仰卧起坐个数在“”的人数占七年级总人数的
七年级总人数为(人)
,
故七年级的学生总人数为360人,a的值为144;
(2)如图所示,
(3)若一分钟标准仰卧起坐在30个以上为合格,该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比为,
故该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比为
20.(1)11
(2)见解析
(1)解:根据题意;
(2)证明:设这个数为,则,
将按,,的顺序运算,得,
,
,
∴,
∴,
结果总大于5.
21.(1)
(2)5
(1)解:点表示的数为,
,
,
的立方根为;
(2)解:由(1)知,
∴
.
22.(1)每辆小客车能坐20名学生,每辆大客车能坐45名学生
(2)共有3种租车方案,方案1:租用24辆小客车,4辆大客车;方案2:租用15辆小客车,8辆大客车;方案3:租用6辆小客车,12辆大客车.
(1)解:设每辆小客车能坐x名学生,每辆大客车能坐y名学生,
根据题意得:,
解得:.
答:每辆小客车能坐20名学生,每辆大客车能坐45名学生;
(2)解:根据题意得:,
∴,
又∵m,n均为正整数,
∴或或,
∴共有3种租车方案,方案1:租用24辆小客车,4辆大客车;方案2:租用15辆小客车,8辆大客车;方案3:租用6辆小客车,12辆大客车.
23.(1)点的坐标为,点到轴的距离为;
(2),第三象限;
(3)
(1)点的“级关联点”的横坐标为,纵坐标为,
点的坐标为,点到轴的距离为;
(2)解:设点的坐标为,
点的“级关联点”为,
,,
解得:,,
点的坐标为,
点所在的象限为第三象限;
(3)解:点的坐标为,
点的“级关联点”为,
,
,
,
,
点的坐标为
24.(1)①;②
(2)
(3)或
(1)解:①,
,
平分,
,
,
,
,
;
②,
,
平分,
,
,
,
,
;
(2)解:,,
,,
平分,
,
;
(3)解:①当在外时,如图1,
设,
由(1)知;
∵,
∴,
∴,
∴;
②当在内时,如图2,
由(2)可知,
,
,,
.
综上,的度数为或.
一、单选题
1.如图,在平面内过点作已知直线的平行线,可作的条数为( )
A.1 B.2 C.3 D.无数条
2.若,且,则的值可能是( )
A. B.0 C.1 D.4
3.下列各项调查适合全面调查的是( )
A.白洋淀中现有鱼的种类 B.某班每位同学的视力情况
C.某品牌节能灯的使用寿命 D.了解某市观众对《哪吒2》的观影感受
4.如图,淇淇从点O出发,先向东走15米,再向北走10米到达点M,如果点M的位置用表示,那么表示的位置是( )
A.点A B.点B C.点C D.点D
5.甲、乙两人求二元一次方程的整数解,甲正确地求出一组解为,乙把看成,求得一组解为,则a,b的值为( )
A. B. C. D.
6.已知点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.下列说法正确的是( )
A.的立方根是 B.的平方根是
C.的算术平方根是3 D.1的平方根是1
8.如图,分别平分与,且.证明.下面是不完整的推理过程,
证明:分别平分与(已知),
___________(角平分线的定义),
(已知),
_________(等量代换),
(已知),
_________,
.
下列说法错误的是( )
A.☆表示 B.表示
C.表示 D.表示内错角相等,两直线平行
9.如图条形统计图、扇形统计图分别是甲、乙两家庭全年支出费用的统计图.根据统计图,对两家庭教育支出费用所作出的判断中,一定正确的是( )
A.甲家庭教育支出费用多于乙家庭
B.甲家庭教育支出费用少于乙家庭
C.甲家庭教育支出费用占比与乙家庭一样
D.甲家庭教育支出费用占比少于乙家庭
10.《九章算术·盈不足》载,其文曰:“今有人共买物,人出八,盈三;人出七,不足四、问人数、物价各几何?“意思为:几个人一起去买东西,如果每人出8钱,就多了3钱;如果每人出7钱,就少了4钱.问一共有多少人?这个物品的价格是多少?设共有人,物品的价格为钱,下列说法错误的是( )
A.由人出八,盈三,可得方程
B.由人出七,不足四,可得方程
C.一共有7人
D.物品的价格为52钱
11.如图,在平面直角坐标系中,.点从点出发,并按的规律在四边形的边上运动,当点运动的路程为2045时,点所在位置的点的坐标为( )
A.点 B.点 C.点 D.点
12.已知关于x的不等式组的整数解为1,2(其中m,n为整数),则满足条件的共有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
13.通常来说,在一定范围内,销售单价越高,月销售量越低,下表记录了某文具的销售单价和月销售量的数据,请你根据月销售量与销售单价的变化趋势,预测当销售单价为16元/个时,月销售量约为 个.
销售单价(元) ... 10 11 12 13 14 ...
月销售量(个) ... 160 149 140 130 120 ...
14.设为正整数,且,则的值为 .
15.如图,直线b、c被直线a所截,如果,,那么与其内错角的角度之和等于 .
16.如图,一个容量为的杯子中装有的水,先将6颗相同的小玻璃球放入这个杯中后,总体积变为,接着依次放入4个相同的小铁块,直到放入第4个后,发现有水溢出.若每个小玻璃球的体积是,每个小铁块的体积是,则下列说法:①;②;③杯子中仅放小铁块,依次放入,放到第8个,水就会溢出;④若杯子中仅放小玻璃球,至少放11个,水才会溢出,正确的是 .(填序号)
三、解答题
17.解不等式组并把解集表示在数轴上.
18.如图,已知,射线交于点,交于点,从点引一条射线,且.
(1)求证:;
(2)若命题“已知___________,则”是真命题,请填空,并说明理由.
19.为了解某校七年级学生一分钟标准仰卧起坐情况,对该校全部七年级学生进行一分钟标准仰卧起坐个数的测试,并把测得数据分成四组,绘制成如下不完整的频数分布表和频数分布直方图(每一组不含前一个边界值,含后一个边界值).已知一分钟标准仰卧起坐个数在“”的人数占七年级总人数的
组别(个) 频数
48
96
a
72
(1)求七年级的学生总人数及a的值;
(2)把频数分布直方图补充完整;
(3)若一分钟标准仰卧起坐在30个以上为合格,求该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比
20.有一个数学游戏,如图有三种运算,每一种运算都是在上一步运算后进行的一步运算.将3按的顺序运算,即.
(1)将按的顺序运算,写出运算过程并求出结果;
(2)若小于的数按的顺序运算,结果总是大于5,请验证这个结论.
21.如图,一只蚂蚁从点沿数轴向右爬行2个单位长度到达点,点表示的数为,设表示的数为.
(1)求的立方根;
(2)求的值.
22.某校八年级660名学生到郊外参加研学活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用2辆小客车和3辆大客车每次可运送学生175人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,恰好每辆车都坐满且两种车都要租,请你设计出所有的租车方案.
23.在平面直角坐标系中,对于点,若点B的坐标为,则称点为点的“级关联点”,如点的“级关联点”点B的坐标为,即
(1)已知点的“级关联点”为,求点的坐标,并写出点到轴的距离;
(2)已知点的“级关联点”为,求点的坐标及所在象限;
(3)如果点的“级关联点”在轴上,求点的坐标.
24.【问题背景】
直线相交于点在的逆时针方向),的平分线在直线上.
(1)【数学理解】
如图1,平分.
①若,求的度数;
②若,请直接写出的度数(用含的代数式表示).
(2)【构建联系】
如图2,平分,若,求的度数(用含的代数式表示).
(3)【总结应用】
若,请直接写出的度数.
参考答案
1.A
解:根据经过经过直线外一点有且只有一条直线与已知直线平行,
故选:A.
2.A
,且,
,
∴的值可能是.
故选:A.
3.B
解: 选项A:白洋淀鱼种类多、分布广,全面调查难度大,适合抽样调查;
选项B:某班学生人数有限,逐一检查视力可行且需精确数据,适合全面调查;
选项C:测试节能灯寿命需破坏性实验,无法普查,适合抽样调查;
选项D:某市观众数量庞大,全面调查成本过高,适合抽样调查;
综上,仅选项B符合全面调查条件;
故选:B
4.B
解:根据先向东走15米,再向北走10米到达点M,且点M的位置用表示,
横坐标用了3个单位长度表示,得到一个单位长度表示5米,
则的横坐标的绝对值为一个单位长度,纵坐标的绝对值是2个单位长度,
故选:B.
5.C
解:由题意可得,
,
解得,
故选C.
6.C
解:∵点在第四象限,
∴,
解得:,
在数轴上表示为:
故选:C.
7.C
解:A. 错误,的立方根是,而非,
B. 错误,,其平方根为,而非,
C. 正确,,其算术平方根为;
D. 错误,1的平方根是,而非仅1;
故选:C
8.C
解:分别平分与(已知),
,A不符合题意;
(已知),
,B不符合题意;
(已知),
,C符合题意;
(内错角相等,两直线平行),D不符合题意;
故选:C
9.D
解:甲家庭教育支出费用占比为;
∵乙家庭教育支出费用占比为,
∴甲家庭教育支出费用占比少于乙家庭,
由于不确定乙家庭支出的总费用,故无法比较甲家庭教育支出费用和乙家庭教育支出费用的多少,
故选D.
10.D
解:设共有人,物价为钱,
根据“每人出8钱,盈3钱”得方程:(选项A正确);
根据“每人出7钱,不足4钱”得方程:(选项B正确);
联立方程组:,
解得:,
因此共有7人(选项C正确);物价为53钱,而选项D中物价为52钱,错误;
故选:D
11.C
解:,,,,
,,
,
点从点出发,并按的规律在四边形的边上运动,
当点运动的路程为2045时,
,
经历次循环,且走5个单位长度,
点所在位置的点的坐标为,即为点;
故选:C.
12.C
解:解不等式得,
;
解不等式得,
;
因为不等式组的整数解为1,2,
所以,且,
则,.
又因为,为整数,
所以,,8,9,
所以满足条件的共有3对.
故选:C
13.100
解:由表可知:售价每增加1元,月销量约减少10个,
∴当销售单价为16元/个时,月销售量比销售单价为14元/个时约减少20个,即约为100个;
故答案为:100.
14.3
解:∵,
∴,
∵,
∴.
故答案为:3.
15./度
解:,
的内错角为,
,
,
与其内错角的角度之和为,
故答案为:.
16.①②④
解:由装有的水,先将6颗相同的小玻璃球放入这个杯中后,总体积变为,得,则①正确;
体积由变为,接着依次放入4个相同的小铁块,直到放入第4个后,发现有水溢出,得,
解得,则②正确;
杯子中仅放小铁块,,
取,,
所以放入8个小铁块,水不一定溢出,则③不正确;
若杯子中仅放小玻璃球,设可以放个,杯子的水会溢出,
则,解得,则④正确.
故答案为:①②④.
17.,数轴上表示见解析
解:解不等式①得,;
解不等式②得,,
所以不等式组的解集为,其解集在数轴上表示如图所示.
.
18.(1)见解析
(2);理由见解析
(1)证明:∵,,,
∴,
∴;
(2)解:,则;
理由:∵,
∴,
∵,
∴,
∵,
∴.
19.(1)七年级的学生总人数为360人,a的值为144
(2)见解析
(3)
(1)解:已知一分钟标准仰卧起坐个数在“”的人数占七年级总人数的
七年级总人数为(人)
,
故七年级的学生总人数为360人,a的值为144;
(2)如图所示,
(3)若一分钟标准仰卧起坐在30个以上为合格,该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比为,
故该校七年级学生仰卧起坐合格的学生人数占七年级学生总人数的百分比为
20.(1)11
(2)见解析
(1)解:根据题意;
(2)证明:设这个数为,则,
将按,,的顺序运算,得,
,
,
∴,
∴,
结果总大于5.
21.(1)
(2)5
(1)解:点表示的数为,
,
,
的立方根为;
(2)解:由(1)知,
∴
.
22.(1)每辆小客车能坐20名学生,每辆大客车能坐45名学生
(2)共有3种租车方案,方案1:租用24辆小客车,4辆大客车;方案2:租用15辆小客车,8辆大客车;方案3:租用6辆小客车,12辆大客车.
(1)解:设每辆小客车能坐x名学生,每辆大客车能坐y名学生,
根据题意得:,
解得:.
答:每辆小客车能坐20名学生,每辆大客车能坐45名学生;
(2)解:根据题意得:,
∴,
又∵m,n均为正整数,
∴或或,
∴共有3种租车方案,方案1:租用24辆小客车,4辆大客车;方案2:租用15辆小客车,8辆大客车;方案3:租用6辆小客车,12辆大客车.
23.(1)点的坐标为,点到轴的距离为;
(2),第三象限;
(3)
(1)点的“级关联点”的横坐标为,纵坐标为,
点的坐标为,点到轴的距离为;
(2)解:设点的坐标为,
点的“级关联点”为,
,,
解得:,,
点的坐标为,
点所在的象限为第三象限;
(3)解:点的坐标为,
点的“级关联点”为,
,
,
,
,
点的坐标为
24.(1)①;②
(2)
(3)或
(1)解:①,
,
平分,
,
,
,
,
;
②,
,
平分,
,
,
,
,
;
(2)解:,,
,,
平分,
,
;
(3)解:①当在外时,如图1,
设,
由(1)知;
∵,
∴,
∴,
∴;
②当在内时,如图2,
由(2)可知,
,
,,
.
综上,的度数为或.
同课章节目录
