河北省承德市丰宁县2024-2025学年七年级下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 河北省承德市丰宁县2024-2025学年七年级下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 22:58:11 | ||
图片预览




文档简介
河北省承德市丰宁县2024-2025学年七年级下学期期末考试数学试题
一、单选题
1.若,则□内的数字是( )
A.3 B. C. D.
2.估计2的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
3.若点在第四象限,那么的取值范围是( )
A. B. C. D.
4.某学校为了解该校800名学生的大课间运动时长,随机抽查了其中80名学生的大课间运动时长并进行统计,下列叙述错误的是( )
A.80名学生的大课间运动时长是总体的一个样本
B.800是样本容量
C.每名学生的大课间运动时长是一个个体
D.以上调查属于抽样调查
5.若,则下列结论正确的是( )
A. B.
C. D.
6.如图,直线、相交于点,平分,若,则的度数为( )
A. B. C. D.
7.已知是关于的二元一次方程的一个解,则的值为( )
A. B. C.4 D.6
8.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为( )cm2
A.6 B.9 C.18 D.24
9.下列运算中,正确的是( )
A. B.
C. D.
10.我国明代有位著名数学家叫程大位,他编撰的《增删算法统宗》里记载“绳索量竿”问题:“一根竿子一条索,索比竿子长一托,折回索子却量竿,却比竿子短一托.问索子与竿子各几何?”“一托”是古代长度单位,大约相当于现在的长.其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长;如果将绳索对折后再去量竿,就比竿短.设绳索长,竿长为,根据题意列二元一次方程组,正确的是( )
A. B.
C. D.
11.若关于x的不等式组无解,则实数a的取值范围是( )
A.a<-4 B.a=-4 C.a>-4 D.a≥-4
12.若,则的平方根是( )
A. B. C. D.
二、填空题
13.如果教室里可以用来表示学生座位的第3行第2列,那么第4行第1列可以用一对数 来表示.
14.规定用符号表示一个实数的整数部分,例如,,按此规律 .
15.在平面直角坐标系中,把点向下平移个单位得到点,则代数式的值为 .
16.一副三角板和按如图方式摆放,其中,点恰好落在上,且,则的度数为 .
三、解答题
17.计算:
(1)解方程:;
(2).
18.嘉琪打算暑假去北京密云游乐场游玩,如图,他根据网上搜到的游乐场的地图,在网格(每个小正方形方格边长都为1)中着重标注了自己特别想游玩的四个地点,其中旋转木马,过山车,摩天轮的坐标分别为,,.
(1)请你根据点,,的坐标建立平面直角坐标系;
(2)写出激流勇进点的坐标_________;
(3)连接,将线段向右平移1个单位长度,再向下平移4个单位长度后,得到线段,画出线段,并直接写出点和点的坐标.
19.(1)解不等式组,并把其解集表示在如图所示的数轴上;
(2)直接写出此不等式组的最小整数解.
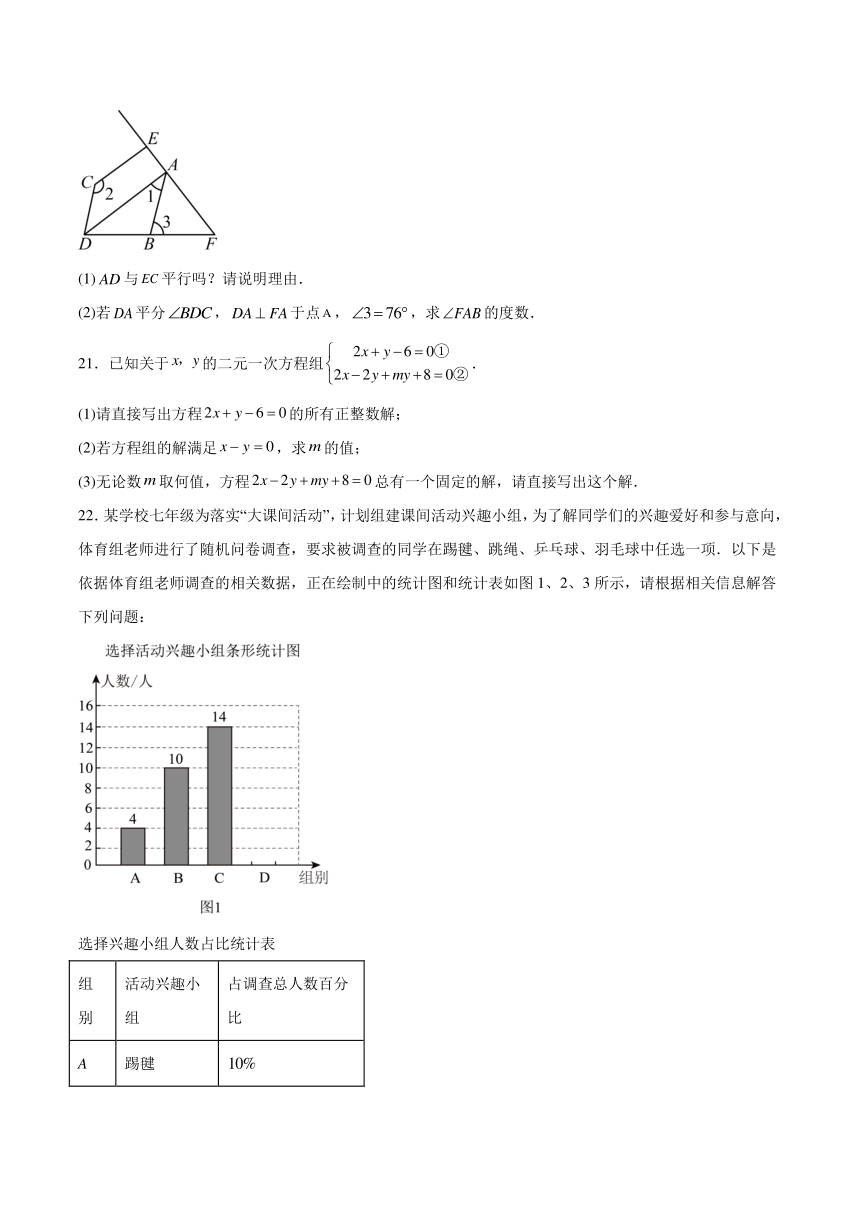
20.如图,已知,.
(1)与平行吗?请说明理由.
(2)若平分,于点,,求的度数.
21.已知关于的二元一次方程组.
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论数取何值,方程总有一个固定的解,请直接写出这个解.
22.某学校七年级为落实“大课间活动”,计划组建课间活动兴趣小组,为了解同学们的兴趣爱好和参与意向,体育组老师进行了随机问卷调查,要求被调查的同学在踢毽、跳绳、乒乓球、羽毛球中任选一项.以下是依据体育组老师调查的相关数据,正在绘制中的统计图和统计表如图1、2、3所示,请根据相关信息解答下列问题:
选择兴趣小组人数占比统计表
组别 活动兴趣小组 占调查总人数百分比
A 踢毽
B 跳绳
C 乒乓球
D 羽毛球
图2
(1)本次体育组老师进行随机问卷调查学生的人数为______人;
(2)请补全上述条形统计图、占比统计表和扇形统计图;
(3)估计该校七年级800名学生中,选择乒乓球兴趣小组的人数.
23.为改善学校环境卫生面貌,计划购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)学校计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个(两种都需要购买),则最多可以购买B型垃圾箱多少个?有几种购买方案?
24.如图1,在平面直角坐标系中,点C在x轴负半轴上,点B在x轴正半轴上,,点,且m、n是方程组的解,与y轴交于点.
(1)直接写出点A、B、C的坐标;
(2)直接写出三角形的面积;
(3)直接写出点D的坐标;
(4)如图2,点P从点D出发,以每秒2个单位长度的速度先沿线段运动到点O不停,再继续以相同的速度沿x轴正半轴运动到点B停止,设运动时间为t秒,求当t为何值时,三角形的面积是三角形面积的2倍.
参考答案
1.B
解:将等式两边同时除以,得:.
故选:B.
2.C
∵(2)2=12,9<12<16,
∴3<2<4.
故选C.
3.A
解:点在第四象限,
,
解得:.
故选:A.
4.B
解:A、样本是从总体中抽取的一部分个体,题目中总体是800名学生的大课间运动时长,随机抽取的80名学生的运动时长数据即为样本,因此说法正确,故此选项不符合题意;
B、样本容量是样本中包含的个体数量,本题中抽取了80名学生,因此样本容量是80,而非总体的数量800,因此说法错误,故此选项符合题意;
C、个体是总体中的每一个考察对象,每名学生的大课间运动时长作为总体中的一个独立数据,属于个体,因此说法正确,故此选项不符合题意;
D、抽样调查是从总体中抽取部分个体进行调查,本题仅抽取80名学生而非全部800名,属于抽样调查,因此说法正确,故此选项不符合题意;
故选:B.
5.C
解:、∵,
∴,此选项不符合题意;
、∵,
∴,此选项不符合题意;
、∵,
∴,此选项符合题意;
、∵,
∴此选项不符合题意;
故选:.
6.B
解:∵平分,,
∴,
∴.
故选:B.
7.B
解:把代入得到,
解得
故选:B
8.C
如图,由题意,长方形ABCD向右平移2cm再向下平移1cm,则长方形的长为:5-2=3(cm),宽为:3-1=2(cm),所以此长方形的面积为:3×2=6(cm2);
同理:长方形的长为2cm,宽为1cm,长方形的长为2cm,宽为1cm,这两个长方形的面积均为1×2=2(cm2);长方形的长为5+2=7(cm),宽为3+1=4(cm),其面积为7×4=28(cm2);
所以阴影部分的面积为:长方形的面积-长方形的面积-长方形的面积-长方形的面积=28-6-2-2=18(cm2)
故选:C.
9.C
解:A、,而非,本选项错误.
B、,结果应为而非,本选项错误.
C、,本选项正确.
D、,而非,本选项错误.
故选:C.
10.A
解:设绳索长,竿长为,
根据题意得,.
故选:A.
11.D
解不等式 得,x<-4,又因这个不等式组无解,根据大大小小无解即可得a≥-4,故答案选D.
12.D
解:∵,
∴,
解得,
∴,
∴的平方根为,
故选:D.
13.
解:因为教室里可以用来表示学生座位的第3行第2列,
所以第4行第1列可以用一对数来表示.
故答案为:.
14.4
解:∵,
∴,即,
∴,
∴,
故答案为:4.
15.
解:∵点把点向下平移个单位得到点,
∴,
整理得,,
∴.
故答案为:.
16.75°/75度
解:,,
,
,,
,
,
故答案为:
17.(1)或
(2)
(1)解:,
,
,
,
,
或.
(2)解:原式
.
18.(1)见解析
(2)
(3)图见解析,,
(1)解:根据题意,建立如图所示的平面直角坐标系.
(2)解:激流勇进点D的坐标为,
故答案为:;
(3)解:画出线段如图所示;
,.
19.(1),数轴见解析;(2)
解:(1)解不等式①得,,
解不等式②得,;
不等式组的解集为.
解集在数轴上表示如图所示.
(2)∵不等式组的解集为.
∴不等式组的整数解为:,0,1,2,3,4
∴不等式组的最小整数解为.
20.(1)平行,理由见解析
(2)
(1)解:与平行.
理由:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴.
21.(1)或
(2)
(3)
(1)由可得:,
为偶数,
为偶数,
为偶数,
,
,
∴
或;
(2),
,
把代入得:
,
解得:,
,
把代入得:
,
解得:
(3),
当时,,
固定解为:.
22.(1)40
(2)见解析
(3)280人
(1)解:,
∴本次体育组老师进行随机问卷调查学生的人数为40人;
(2)解:依题意,调查学生的人数为40人;
∴,,,,
条形统计图如图所示:
占比统计表如图所示:
组别 活动兴趣小组 占调查总人数百分比
A 踢毽
B 跳绳
C 乒乓球
D 羽毛球
扇形统计图如图所示:
(3)解:依题意,人;
答:估计该校七年级800名学生中,选择乒乓球兴趣小组的人数为280人.
23.(1)每个A型垃圾箱100元,每个B型垃圾箱120元;(2)最多可以购买B型垃圾箱5个,共有5种购货方案
解:(1)设每个A型垃圾箱x元,B型垃圾箱y元,依题意得:
,
解得:,
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
(2)设购买B型垃圾箱m个,则购买A型垃圾箱(20﹣m)个,
依题意有:120m+100(20﹣m)≤2100,
解得:m≤5.
∵两种垃圾箱都要购买,
∴0<m≤5且m为整数,
∴m=1,2,3,4,5,
答:该小区最多可以购买B型垃圾箱5个,共有5种购货方案.
24.(1)、、
(2)35
(3)点D的坐标为;
(4)当或时,的面积是面积的2倍.
(1)解:∵点C在x轴负半轴上,点B在x轴正半轴上,,
∴、,
解方程组,
得,
∴点A的坐标是;
(2)解:过点A作轴于点H,
∵,、,
∴,,
∴;
(3)解:连接,
∵,
∴,
∴,
∴点D的坐标为;
(4)解:①当点P在线段上,,
∵,
∴,
解得:;
②当点P在线段上时,
∵,
∴,
解得:;
综上所述当或时,的面积是面积的2倍.
一、单选题
1.若,则□内的数字是( )
A.3 B. C. D.
2.估计2的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
3.若点在第四象限,那么的取值范围是( )
A. B. C. D.
4.某学校为了解该校800名学生的大课间运动时长,随机抽查了其中80名学生的大课间运动时长并进行统计,下列叙述错误的是( )
A.80名学生的大课间运动时长是总体的一个样本
B.800是样本容量
C.每名学生的大课间运动时长是一个个体
D.以上调查属于抽样调查
5.若,则下列结论正确的是( )
A. B.
C. D.
6.如图,直线、相交于点,平分,若,则的度数为( )
A. B. C. D.
7.已知是关于的二元一次方程的一个解,则的值为( )
A. B. C.4 D.6
8.如图,将长为,宽为的长方形先向右平移,再向下平移,得到长方形,则阴影部分的面积为( )cm2
A.6 B.9 C.18 D.24
9.下列运算中,正确的是( )
A. B.
C. D.
10.我国明代有位著名数学家叫程大位,他编撰的《增删算法统宗》里记载“绳索量竿”问题:“一根竿子一条索,索比竿子长一托,折回索子却量竿,却比竿子短一托.问索子与竿子各几何?”“一托”是古代长度单位,大约相当于现在的长.其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长;如果将绳索对折后再去量竿,就比竿短.设绳索长,竿长为,根据题意列二元一次方程组,正确的是( )
A. B.
C. D.
11.若关于x的不等式组无解,则实数a的取值范围是( )
A.a<-4 B.a=-4 C.a>-4 D.a≥-4
12.若,则的平方根是( )
A. B. C. D.
二、填空题
13.如果教室里可以用来表示学生座位的第3行第2列,那么第4行第1列可以用一对数 来表示.
14.规定用符号表示一个实数的整数部分,例如,,按此规律 .
15.在平面直角坐标系中,把点向下平移个单位得到点,则代数式的值为 .
16.一副三角板和按如图方式摆放,其中,点恰好落在上,且,则的度数为 .
三、解答题
17.计算:
(1)解方程:;
(2).
18.嘉琪打算暑假去北京密云游乐场游玩,如图,他根据网上搜到的游乐场的地图,在网格(每个小正方形方格边长都为1)中着重标注了自己特别想游玩的四个地点,其中旋转木马,过山车,摩天轮的坐标分别为,,.
(1)请你根据点,,的坐标建立平面直角坐标系;
(2)写出激流勇进点的坐标_________;
(3)连接,将线段向右平移1个单位长度,再向下平移4个单位长度后,得到线段,画出线段,并直接写出点和点的坐标.
19.(1)解不等式组,并把其解集表示在如图所示的数轴上;
(2)直接写出此不等式组的最小整数解.
20.如图,已知,.
(1)与平行吗?请说明理由.
(2)若平分,于点,,求的度数.
21.已知关于的二元一次方程组.
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论数取何值,方程总有一个固定的解,请直接写出这个解.
22.某学校七年级为落实“大课间活动”,计划组建课间活动兴趣小组,为了解同学们的兴趣爱好和参与意向,体育组老师进行了随机问卷调查,要求被调查的同学在踢毽、跳绳、乒乓球、羽毛球中任选一项.以下是依据体育组老师调查的相关数据,正在绘制中的统计图和统计表如图1、2、3所示,请根据相关信息解答下列问题:
选择兴趣小组人数占比统计表
组别 活动兴趣小组 占调查总人数百分比
A 踢毽
B 跳绳
C 乒乓球
D 羽毛球
图2
(1)本次体育组老师进行随机问卷调查学生的人数为______人;
(2)请补全上述条形统计图、占比统计表和扇形统计图;
(3)估计该校七年级800名学生中,选择乒乓球兴趣小组的人数.
23.为改善学校环境卫生面貌,计划购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)学校计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个(两种都需要购买),则最多可以购买B型垃圾箱多少个?有几种购买方案?
24.如图1,在平面直角坐标系中,点C在x轴负半轴上,点B在x轴正半轴上,,点,且m、n是方程组的解,与y轴交于点.
(1)直接写出点A、B、C的坐标;
(2)直接写出三角形的面积;
(3)直接写出点D的坐标;
(4)如图2,点P从点D出发,以每秒2个单位长度的速度先沿线段运动到点O不停,再继续以相同的速度沿x轴正半轴运动到点B停止,设运动时间为t秒,求当t为何值时,三角形的面积是三角形面积的2倍.
参考答案
1.B
解:将等式两边同时除以,得:.
故选:B.
2.C
∵(2)2=12,9<12<16,
∴3<2<4.
故选C.
3.A
解:点在第四象限,
,
解得:.
故选:A.
4.B
解:A、样本是从总体中抽取的一部分个体,题目中总体是800名学生的大课间运动时长,随机抽取的80名学生的运动时长数据即为样本,因此说法正确,故此选项不符合题意;
B、样本容量是样本中包含的个体数量,本题中抽取了80名学生,因此样本容量是80,而非总体的数量800,因此说法错误,故此选项符合题意;
C、个体是总体中的每一个考察对象,每名学生的大课间运动时长作为总体中的一个独立数据,属于个体,因此说法正确,故此选项不符合题意;
D、抽样调查是从总体中抽取部分个体进行调查,本题仅抽取80名学生而非全部800名,属于抽样调查,因此说法正确,故此选项不符合题意;
故选:B.
5.C
解:、∵,
∴,此选项不符合题意;
、∵,
∴,此选项不符合题意;
、∵,
∴,此选项符合题意;
、∵,
∴此选项不符合题意;
故选:.
6.B
解:∵平分,,
∴,
∴.
故选:B.
7.B
解:把代入得到,
解得
故选:B
8.C
如图,由题意,长方形ABCD向右平移2cm再向下平移1cm,则长方形的长为:5-2=3(cm),宽为:3-1=2(cm),所以此长方形的面积为:3×2=6(cm2);
同理:长方形的长为2cm,宽为1cm,长方形的长为2cm,宽为1cm,这两个长方形的面积均为1×2=2(cm2);长方形的长为5+2=7(cm),宽为3+1=4(cm),其面积为7×4=28(cm2);
所以阴影部分的面积为:长方形的面积-长方形的面积-长方形的面积-长方形的面积=28-6-2-2=18(cm2)
故选:C.
9.C
解:A、,而非,本选项错误.
B、,结果应为而非,本选项错误.
C、,本选项正确.
D、,而非,本选项错误.
故选:C.
10.A
解:设绳索长,竿长为,
根据题意得,.
故选:A.
11.D
解不等式 得,x<-4,又因这个不等式组无解,根据大大小小无解即可得a≥-4,故答案选D.
12.D
解:∵,
∴,
解得,
∴,
∴的平方根为,
故选:D.
13.
解:因为教室里可以用来表示学生座位的第3行第2列,
所以第4行第1列可以用一对数来表示.
故答案为:.
14.4
解:∵,
∴,即,
∴,
∴,
故答案为:4.
15.
解:∵点把点向下平移个单位得到点,
∴,
整理得,,
∴.
故答案为:.
16.75°/75度
解:,,
,
,,
,
,
故答案为:
17.(1)或
(2)
(1)解:,
,
,
,
,
或.
(2)解:原式
.
18.(1)见解析
(2)
(3)图见解析,,
(1)解:根据题意,建立如图所示的平面直角坐标系.
(2)解:激流勇进点D的坐标为,
故答案为:;
(3)解:画出线段如图所示;
,.
19.(1),数轴见解析;(2)
解:(1)解不等式①得,,
解不等式②得,;
不等式组的解集为.
解集在数轴上表示如图所示.
(2)∵不等式组的解集为.
∴不等式组的整数解为:,0,1,2,3,4
∴不等式组的最小整数解为.
20.(1)平行,理由见解析
(2)
(1)解:与平行.
理由:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∵,
∴,
∴.
21.(1)或
(2)
(3)
(1)由可得:,
为偶数,
为偶数,
为偶数,
,
,
∴
或;
(2),
,
把代入得:
,
解得:,
,
把代入得:
,
解得:
(3),
当时,,
固定解为:.
22.(1)40
(2)见解析
(3)280人
(1)解:,
∴本次体育组老师进行随机问卷调查学生的人数为40人;
(2)解:依题意,调查学生的人数为40人;
∴,,,,
条形统计图如图所示:
占比统计表如图所示:
组别 活动兴趣小组 占调查总人数百分比
A 踢毽
B 跳绳
C 乒乓球
D 羽毛球
扇形统计图如图所示:
(3)解:依题意,人;
答:估计该校七年级800名学生中,选择乒乓球兴趣小组的人数为280人.
23.(1)每个A型垃圾箱100元,每个B型垃圾箱120元;(2)最多可以购买B型垃圾箱5个,共有5种购货方案
解:(1)设每个A型垃圾箱x元,B型垃圾箱y元,依题意得:
,
解得:,
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
(2)设购买B型垃圾箱m个,则购买A型垃圾箱(20﹣m)个,
依题意有:120m+100(20﹣m)≤2100,
解得:m≤5.
∵两种垃圾箱都要购买,
∴0<m≤5且m为整数,
∴m=1,2,3,4,5,
答:该小区最多可以购买B型垃圾箱5个,共有5种购货方案.
24.(1)、、
(2)35
(3)点D的坐标为;
(4)当或时,的面积是面积的2倍.
(1)解:∵点C在x轴负半轴上,点B在x轴正半轴上,,
∴、,
解方程组,
得,
∴点A的坐标是;
(2)解:过点A作轴于点H,
∵,、,
∴,,
∴;
(3)解:连接,
∵,
∴,
∴,
∴点D的坐标为;
(4)解:①当点P在线段上,,
∵,
∴,
解得:;
②当点P在线段上时,
∵,
∴,
解得:;
综上所述当或时,的面积是面积的2倍.
同课章节目录
