2025年秋沪科版七年级数学上册 1.6 有理数的乘方 课件(共38张PPT)
文档属性
| 名称 | 2025年秋沪科版七年级数学上册 1.6 有理数的乘方 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 22:59:18 | ||
图片预览









文档简介
(共38张PPT)
1.6 有理数的乘方
第一章 有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
乘方的意义
乘方的运算法则
有理数的混合运算
用科学记数法表示数
知1-讲
感悟新知
知识点
乘方的意义
1
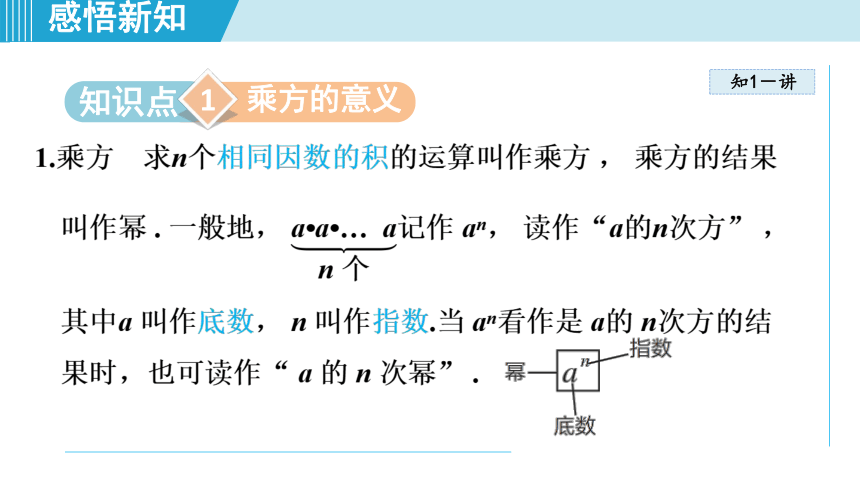
1.乘方 求n个相同因数的积的运算叫作乘方 , 乘方的结果叫作幂 . 一般地, 记作 an, 读作“a的n次方” ,其中a 叫作底数, n 叫作指数.当 an看作是 a的 n次方的结果时,也可读作“ a 的 n 次幂” .
感悟新知
知1-讲
特别提醒
1. 有理数的乘方可以看作是一种特殊的乘法运算 .
2. 乘方具有双重意义,它不仅表示一种运算——求几个相同因数的积的运算,还表示这种运算的结果——幂.
感悟新知
2. 乘方的意义 an 表示 n 个相同因数 a 的积,其中相同的因数是底数,因数的个数是指数,因此,可以把相同因数的乘法转化为乘方或把乘方转化为乘法 .
知1-讲
知1-练
感悟新知
填空: (1)(- 2) 5的底数是 _____ ,指数是 _____ ,
它表示 __________________________________ ;
(2) - 25的底数是 _____ ,指数是_____ ,它表示 ___________________ ;
(3) (- )2的底数是 _____,指数是_____ ,它表示 _________________.
例1
-2
5
(-2) × (-2) × (-2) × (-2) × (-2)
2
5
-2× 2× 2× 2× 2
-
2
(- × (- )
知1-练
感悟新知
解:(1) (- 2) 5 的底数是 - 2 ,指数是 5,
它表示(- 2) × (- 2) × (- 2) × (- 2) × (- 2) .
(2) - 25 的底数是 2,指数是 5,
它表示 - 2× 2× 2× 2× 2.
(3)(- )2的底数是 (- ) ,指数是 2,
它表示 (- ) × (- ).
解题秘方:利用乘方的意义确定底数和指数.
知1-练
感悟新知
1-1. [期中· 安庆] 下列说法正确的是( )
A. - 28的底数是- 2
B. 25表示5个2相加
C.(- 3) 3与- 33意义相同
D. - 的底数是2
D
感悟新知
知2-讲
知识点
乘方的运算法则
2
1. 有理数的乘方运算法则 求非 0 有理数的乘方,将其绝对值乘方,并取符号:正数的任意次幂都取正号;负数的奇次幂取负号,负数的偶次幂取正号 .
感悟新知
知2-讲
2. 有理数的乘方运算 计算一个有理数的乘方时,应将乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值 . 特别地,当底数较大时,可借助于计算器计算 .
知2-讲
感悟新知
特别解读
1. 有理数的乘方运算法则主要揭示幂的符号法则.一看底数,二看指数,确定符号后还是按照有理数的乘法算出其结果.
2. 互为相反数的两个非0 有理数的奇次幂仍然互为相反数 .
3. 互为相反数的两个非 0 有理数的偶次幂相等.
感悟新知
知2-讲
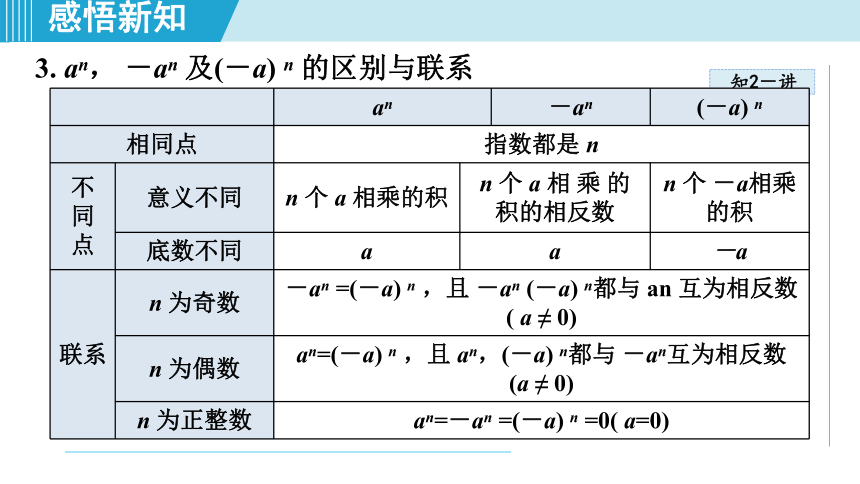
3. an, -an 及(-a) n 的区别与联系
an -an (-a) n
相同点 指数都是 n 不 同 点 意义不同 n 个 a 相乘的积 n 个 a 相 乘 的积的相反数 n 个 -a相乘的积
底数不同 a a -a
联系 n 为奇数 -an =(-a) n ,且 -an (-a) n都与 an 互为相反数( a ≠ 0) n 为偶数 an=(-a) n ,且 an,(-a) n都与 -an互为相反数 (a ≠ 0) n 为正整数 an=-an =(-a) n =0( a=0)
感悟新知
知2-练
计算: (1)(- 5) 4; (2) - 54; (3) ()3;
(4) (- )3; (5)(- 1) 2 024; (6) (- 1 ) 4.
例2
解题秘方:先确定幂的符号,然后转化为乘法运算算出结果.
知2-练
感悟新知
解:(- 5) 4=+(5× 5× 5× 5) =625.
(1)(- 5) 4;
(2) - 54;
(3) ()3;
(4) (- )3;
- 54 = -(5× 5× 5× 5) = - 625.
()3 =+( × × ) = .
(- )3 = - ××= - .
知2-练
感悟新知
解:(- 1) 2 024=+ =1.
(5)(- 1) 2 024;
(6) (- 1 ) 4.
(- 1 ) 4 = (- ) 4=
+(× × × )= .
-1的奇次幂等于-1,
-1的偶次幂等于1.
求带分数的乘方时,要先
把带分数化成假分数,再
利用乘方的运算法则计算.
知2-练
感悟新知
2-1.下列各组数中,互为相反数的是( )
① -(- 3)和- | - 3|;②(- 2)4和- 24;
③(- 2)4和(- 3)2;④(- 2)3和- 23.
A. ①② B. ①②③
C. ①②④ D. ②
A
感悟新知
知3-讲
知识点
有理数的混合运算
3
1. 有理数运算的种类 有理数的混合运算包括加、减、乘、除、乘方与开方(将在以后学习到) . 通常把六种基本的代数运算分为三级:
加与减是第一级运算;乘与除是第二级运算;
乘方与开方是第三级运算 .
感悟新知
知3-讲
活学巧记
混合运算分三级,
运算顺序高到低,
乘方、乘除再加减,
括号内运算最优先 .
感悟新知
知3-讲
2. 有理数混合运算的顺序
(1)先算高级运算,再算低级运算,即:先乘方,再乘除,最后加减;
(2) 同级运算,按从左到右的顺序进行;
(3) 如有括号,先进行括号内的运算,按小括号、中括号、大括号依次进行 .
知3-讲
感悟新知
特别提醒
在运算过程中,一般将小数化为分数,将带分数化为假分数,然后再进行计算.
知3-练
感悟新知
计算: (1) - 72+2×(- 3) 2+(- 6)÷ (- )2;
(2) [(1 - )2 -( - 1 ) ÷ (- 1 ) ] ×( - 1 ) 3.
例3
解题秘方:按有理数混合运算的顺序计算 .
知3-练
感悟新知
解:原式 = - 49+2× 9+ (- 6) × 9
= - 49+18+ (- 54)
= - 85.
(1) - 72+2×(- 3) 2+(- 6)÷ (- )2;
知3-练
感悟新知
解:原式 = [()2 -( - ) × (- ) ] ×( - )
= (- × ) ×( - )
=×( - ) - × ×( - )
= - +5
=3 .
(2) [(1 - )2 -( - 1 ) ÷ (- 1 ) ] ×( - 1 ) 3.
知3-练
感悟新知
3-1.计算: (1) - 14+ 16 ÷(- 2) 3× |-3-1|;
解:原式=-1+16÷(-8)×4=-1-8=-9.
知3-练
感悟新知
(2)(-2) 3÷(-32)+( - )×(-24);
(3) -12- ×[2- (-3)2]÷(-7).
感悟新知
知4-讲
知识点
用科学记数法表示数
4
1. 科学记数法 一般地,绝对值大于10的数可以记成 ± a× 10n的形式,其中1 ≤ |a|<10, n等于原数的整数位数减1.
感悟新知
知4-讲
2. 科学记数法中的 a 和 n
(1)将原数的小数点移到最高数位的数字的后边即可得到 a的值 .
(2)确定 n 的两种方法:
①根据原数的整数位数来确定 n, n 等于原数的整数位数减 1. 例如 2 024 是一个四位整数,用科学记数法表示为 2.024× 10 3,其中 n=4 - 1=3;
②按小数点移动的位数来确定 n,小数点向左移动了几位, n 就等于几 .
知4-讲
感悟新知
特别提醒
1. 用科学记数法表示数只是改变数的形式,不改变数的性质和大小.
2. 用科学记数法表示负数时和正数一样,区别就是前面多一个“-”号.
知4-练
感悟新知
用科学记数法表示下列各数:
(1) 12 000; (2) - 2 021 000 000; (3) 14 000 万 .
解题秘方:在用科学记数法将一个绝对值大于 10 的数表示成 a× 10 n 的形式时, 1 ≤ |a|<10, n 为正整数 .
例4
12 000;
(2) - 2 021 000 000;
(3) 14 000 万 .
知4-练
感悟新知
解:12 000=1.2× 10 4.
- 2 021 000 000= - 2.021× 10 9.
14 000 万 =14 000× 10 000=140 000 000=1.4× 10 8.
知4-练
感悟新知
4-1. [中考·浙江] 2024年浙江经济一季度GDP为 201 370 000万元,其中201 370 000用科学记数法表示为( )
A. 20.137× 109
B. 0.201 37× 108
C. 2.013 7× 109
D. 2.013 7× 108
D
感悟新知
知4-练
已知下列用科学记数法表示的数,写出原来的数:
(1) 2.01× 104;
(2) 6.07× 105;
(3) -3× 103.
例5
解题秘方:将用科学记数法表示的数 ± a× 10 n 还原成原数时,把 a 中的小数点向右移动 n 位,并去掉乘号和 10 n 即可.
知4-练
感悟新知
解:2.01× 10 4=20 100.
6.07× 10 5=607 000.
-3× 103 =-3 000.
(1) 2.01× 104;
(2) 6.07× 105;
(3) -3× 103.
把用科学记数法表示的
数 ±a×10n 还原后,
其整数位数应为 n+1.
知4-练
感悟新知
5-1. ChatGPT是人工智能研究实验室OpenAI推出的 一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达1.75× 1011个模型参数.数据1.75× 1011的位数为__________
12
感悟新知
知4-练
比较大小: 9.523× 1010与 1.002× 1011.
例6
解题秘方:先还原两个用科学记数法表示的数,再比较大小.
解:9.523× 10 10=95 230 000 000,
1.002× 10 11=100 200 000 000.
因为 95 230 000 000<100 200 000 000,
所以 9.523× 10 10<1.002× 10 11.
知4-练
感悟新知
方法点拨:比较用科学记数法表示的两个数的大小的方法:
(1) 若两个数都是正数,先看 n, n 大的原数就大;若 n 相同,则 a(此时 a>0)大的原数就大 .
(2)若是两个负数,则刚好相反, n 大的原数就小;若 n 相同,则 |a|(此时 a<0)大的原数就小 .
知4-练
感悟新知
6-1.用“<” 或“>” 填空:
(1)7.58× 106_______2× 107;
(2) -9.6× 105_________-4.31× 106.
<
>
有理数的
乘方
科学计数法
有理数的
混合运算
乘方
乘方的意义
乘方的运算
1.6 有理数的乘方
第一章 有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
乘方的意义
乘方的运算法则
有理数的混合运算
用科学记数法表示数
知1-讲
感悟新知
知识点
乘方的意义
1
1.乘方 求n个相同因数的积的运算叫作乘方 , 乘方的结果叫作幂 . 一般地, 记作 an, 读作“a的n次方” ,其中a 叫作底数, n 叫作指数.当 an看作是 a的 n次方的结果时,也可读作“ a 的 n 次幂” .
感悟新知
知1-讲
特别提醒
1. 有理数的乘方可以看作是一种特殊的乘法运算 .
2. 乘方具有双重意义,它不仅表示一种运算——求几个相同因数的积的运算,还表示这种运算的结果——幂.
感悟新知
2. 乘方的意义 an 表示 n 个相同因数 a 的积,其中相同的因数是底数,因数的个数是指数,因此,可以把相同因数的乘法转化为乘方或把乘方转化为乘法 .
知1-讲
知1-练
感悟新知
填空: (1)(- 2) 5的底数是 _____ ,指数是 _____ ,
它表示 __________________________________ ;
(2) - 25的底数是 _____ ,指数是_____ ,它表示 ___________________ ;
(3) (- )2的底数是 _____,指数是_____ ,它表示 _________________.
例1
-2
5
(-2) × (-2) × (-2) × (-2) × (-2)
2
5
-2× 2× 2× 2× 2
-
2
(- × (- )
知1-练
感悟新知
解:(1) (- 2) 5 的底数是 - 2 ,指数是 5,
它表示(- 2) × (- 2) × (- 2) × (- 2) × (- 2) .
(2) - 25 的底数是 2,指数是 5,
它表示 - 2× 2× 2× 2× 2.
(3)(- )2的底数是 (- ) ,指数是 2,
它表示 (- ) × (- ).
解题秘方:利用乘方的意义确定底数和指数.
知1-练
感悟新知
1-1. [期中· 安庆] 下列说法正确的是( )
A. - 28的底数是- 2
B. 25表示5个2相加
C.(- 3) 3与- 33意义相同
D. - 的底数是2
D
感悟新知
知2-讲
知识点
乘方的运算法则
2
1. 有理数的乘方运算法则 求非 0 有理数的乘方,将其绝对值乘方,并取符号:正数的任意次幂都取正号;负数的奇次幂取负号,负数的偶次幂取正号 .
感悟新知
知2-讲
2. 有理数的乘方运算 计算一个有理数的乘方时,应将乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值 . 特别地,当底数较大时,可借助于计算器计算 .
知2-讲
感悟新知
特别解读
1. 有理数的乘方运算法则主要揭示幂的符号法则.一看底数,二看指数,确定符号后还是按照有理数的乘法算出其结果.
2. 互为相反数的两个非0 有理数的奇次幂仍然互为相反数 .
3. 互为相反数的两个非 0 有理数的偶次幂相等.
感悟新知
知2-讲
3. an, -an 及(-a) n 的区别与联系
an -an (-a) n
相同点 指数都是 n 不 同 点 意义不同 n 个 a 相乘的积 n 个 a 相 乘 的积的相反数 n 个 -a相乘的积
底数不同 a a -a
联系 n 为奇数 -an =(-a) n ,且 -an (-a) n都与 an 互为相反数( a ≠ 0) n 为偶数 an=(-a) n ,且 an,(-a) n都与 -an互为相反数 (a ≠ 0) n 为正整数 an=-an =(-a) n =0( a=0)
感悟新知
知2-练
计算: (1)(- 5) 4; (2) - 54; (3) ()3;
(4) (- )3; (5)(- 1) 2 024; (6) (- 1 ) 4.
例2
解题秘方:先确定幂的符号,然后转化为乘法运算算出结果.
知2-练
感悟新知
解:(- 5) 4=+(5× 5× 5× 5) =625.
(1)(- 5) 4;
(2) - 54;
(3) ()3;
(4) (- )3;
- 54 = -(5× 5× 5× 5) = - 625.
()3 =+( × × ) = .
(- )3 = - ××= - .
知2-练
感悟新知
解:(- 1) 2 024=+ =1.
(5)(- 1) 2 024;
(6) (- 1 ) 4.
(- 1 ) 4 = (- ) 4=
+(× × × )= .
-1的奇次幂等于-1,
-1的偶次幂等于1.
求带分数的乘方时,要先
把带分数化成假分数,再
利用乘方的运算法则计算.
知2-练
感悟新知
2-1.下列各组数中,互为相反数的是( )
① -(- 3)和- | - 3|;②(- 2)4和- 24;
③(- 2)4和(- 3)2;④(- 2)3和- 23.
A. ①② B. ①②③
C. ①②④ D. ②
A
感悟新知
知3-讲
知识点
有理数的混合运算
3
1. 有理数运算的种类 有理数的混合运算包括加、减、乘、除、乘方与开方(将在以后学习到) . 通常把六种基本的代数运算分为三级:
加与减是第一级运算;乘与除是第二级运算;
乘方与开方是第三级运算 .
感悟新知
知3-讲
活学巧记
混合运算分三级,
运算顺序高到低,
乘方、乘除再加减,
括号内运算最优先 .
感悟新知
知3-讲
2. 有理数混合运算的顺序
(1)先算高级运算,再算低级运算,即:先乘方,再乘除,最后加减;
(2) 同级运算,按从左到右的顺序进行;
(3) 如有括号,先进行括号内的运算,按小括号、中括号、大括号依次进行 .
知3-讲
感悟新知
特别提醒
在运算过程中,一般将小数化为分数,将带分数化为假分数,然后再进行计算.
知3-练
感悟新知
计算: (1) - 72+2×(- 3) 2+(- 6)÷ (- )2;
(2) [(1 - )2 -( - 1 ) ÷ (- 1 ) ] ×( - 1 ) 3.
例3
解题秘方:按有理数混合运算的顺序计算 .
知3-练
感悟新知
解:原式 = - 49+2× 9+ (- 6) × 9
= - 49+18+ (- 54)
= - 85.
(1) - 72+2×(- 3) 2+(- 6)÷ (- )2;
知3-练
感悟新知
解:原式 = [()2 -( - ) × (- ) ] ×( - )
= (- × ) ×( - )
=×( - ) - × ×( - )
= - +5
=3 .
(2) [(1 - )2 -( - 1 ) ÷ (- 1 ) ] ×( - 1 ) 3.
知3-练
感悟新知
3-1.计算: (1) - 14+ 16 ÷(- 2) 3× |-3-1|;
解:原式=-1+16÷(-8)×4=-1-8=-9.
知3-练
感悟新知
(2)(-2) 3÷(-32)+( - )×(-24);
(3) -12- ×[2- (-3)2]÷(-7).
感悟新知
知4-讲
知识点
用科学记数法表示数
4
1. 科学记数法 一般地,绝对值大于10的数可以记成 ± a× 10n的形式,其中1 ≤ |a|<10, n等于原数的整数位数减1.
感悟新知
知4-讲
2. 科学记数法中的 a 和 n
(1)将原数的小数点移到最高数位的数字的后边即可得到 a的值 .
(2)确定 n 的两种方法:
①根据原数的整数位数来确定 n, n 等于原数的整数位数减 1. 例如 2 024 是一个四位整数,用科学记数法表示为 2.024× 10 3,其中 n=4 - 1=3;
②按小数点移动的位数来确定 n,小数点向左移动了几位, n 就等于几 .
知4-讲
感悟新知
特别提醒
1. 用科学记数法表示数只是改变数的形式,不改变数的性质和大小.
2. 用科学记数法表示负数时和正数一样,区别就是前面多一个“-”号.
知4-练
感悟新知
用科学记数法表示下列各数:
(1) 12 000; (2) - 2 021 000 000; (3) 14 000 万 .
解题秘方:在用科学记数法将一个绝对值大于 10 的数表示成 a× 10 n 的形式时, 1 ≤ |a|<10, n 为正整数 .
例4
12 000;
(2) - 2 021 000 000;
(3) 14 000 万 .
知4-练
感悟新知
解:12 000=1.2× 10 4.
- 2 021 000 000= - 2.021× 10 9.
14 000 万 =14 000× 10 000=140 000 000=1.4× 10 8.
知4-练
感悟新知
4-1. [中考·浙江] 2024年浙江经济一季度GDP为 201 370 000万元,其中201 370 000用科学记数法表示为( )
A. 20.137× 109
B. 0.201 37× 108
C. 2.013 7× 109
D. 2.013 7× 108
D
感悟新知
知4-练
已知下列用科学记数法表示的数,写出原来的数:
(1) 2.01× 104;
(2) 6.07× 105;
(3) -3× 103.
例5
解题秘方:将用科学记数法表示的数 ± a× 10 n 还原成原数时,把 a 中的小数点向右移动 n 位,并去掉乘号和 10 n 即可.
知4-练
感悟新知
解:2.01× 10 4=20 100.
6.07× 10 5=607 000.
-3× 103 =-3 000.
(1) 2.01× 104;
(2) 6.07× 105;
(3) -3× 103.
把用科学记数法表示的
数 ±a×10n 还原后,
其整数位数应为 n+1.
知4-练
感悟新知
5-1. ChatGPT是人工智能研究实验室OpenAI推出的 一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达1.75× 1011个模型参数.数据1.75× 1011的位数为__________
12
感悟新知
知4-练
比较大小: 9.523× 1010与 1.002× 1011.
例6
解题秘方:先还原两个用科学记数法表示的数,再比较大小.
解:9.523× 10 10=95 230 000 000,
1.002× 10 11=100 200 000 000.
因为 95 230 000 000<100 200 000 000,
所以 9.523× 10 10<1.002× 10 11.
知4-练
感悟新知
方法点拨:比较用科学记数法表示的两个数的大小的方法:
(1) 若两个数都是正数,先看 n, n 大的原数就大;若 n 相同,则 a(此时 a>0)大的原数就大 .
(2)若是两个负数,则刚好相反, n 大的原数就小;若 n 相同,则 |a|(此时 a<0)大的原数就小 .
知4-练
感悟新知
6-1.用“<” 或“>” 填空:
(1)7.58× 106_______2× 107;
(2) -9.6× 105_________-4.31× 106.
<
>
有理数的
乘方
科学计数法
有理数的
混合运算
乘方
乘方的意义
乘方的运算
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
