14.1 全等三角形及其性质 教学设计 2025-2026学年数学人教版(2024)八年级上册
文档属性
| 名称 | 14.1 全等三角形及其性质 教学设计 2025-2026学年数学人教版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 00:00:00 | ||
图片预览




文档简介
第十四章 全等三角形
14.1 全等三角形及其性质
【教学目标】
1.知道什么是全等形,全等三角形以及全等三角形对应的元素.
2.能用符号正确地表示两个三角形全等.
3.能够从图形中寻找全等三角形,能熟练地找出两个全等三角形的对应顶点、对应边、对应角.
4.探索并掌握全等三角形的性质,能够利用性质解决简单的问题.
5.经历探索全等三角形性质的过程,能在全等三角形中正确找出对应边、对应角.
【重点难点】
重点:全等三角形以及相关概念.探索全等三角形的性质.
难点:掌握找对应边、对应角的方法.
【教学过程】
一、创设情境,导入新课
[复习旧知]
1.用多媒体展示生活中的大量图形的形状与大小完全相同的图片或录像片断.
2.教师出示演示课件:庐山风景,以诗“横看成岭侧成峰,远近高低各不同,不识庐山真面目,只缘身在此山中”指出大自然中庐山的唯一性,但是我们可以通过摄影把庐山的美景拍下来,可以洗出千万张一模一样的庐山相片.
这种形状与大小完全相同的图形就是全等形,那什么是全等形 全等形具有什么性质 这一节课我们就来学习.
二、探究归纳
活动一:探究全等形的概念
【问题】按照教科书的要求,将一块三角尺按在纸板上,画出图形,按照图形裁下纸板.观察裁下的纸板的形状、大小是否完全一样,能否完全重合
答案:能够完全重合.
1.你还能说一说自己身边还有哪些形状和大小都相同的图形吗
(1)全等形:能够完全重合的两个图形叫作全等形.
(2)全等形的判别方法:
两个图形→即完全重合.
2.全等三角形的定义和表示方法
(1)全等三角形的定义:能够完全重合的两个三角形叫作全等三角形.
全等三角形是特殊的全等形.
(2)对应元素:
把两个全等的三角形重合到一起:
①对应顶点:重合的顶点;
②对应边:重合的边;
③对应角:重合的角.
如图,△ABC与△DEF全等.
对应顶点有:点A和点D,点B和点E,点C和点F;
对应边有:AB和DE,BC和EF,AC和DF.
对应角有:∠A和∠D,∠B和∠E,∠C和∠F.
(3)表示方法:
“全等”用“≌”表示,读作“全等于”.
例如,△ABC与△A'B'C'全等,点A和点A',点B和点B',点C和点C'是对应顶点,记作△ABC≌△A'B'C'.
以上我们学习了全等三角形的概念,知道了什么是全等三角形.下面我们研究一下怎样的图形变换得到全等三角形.
活动二:全等三角形中的全等变换
【问题】只改变图形的位置,而不改变其形状、大小的变换,叫作全等变换.平移、翻折、旋转都属于全等变换.
一个三角形经过全等变换,位置发生了变化,但其形状、大小未发生变化.通过观察两个全等三角形中的一个经过怎样的全等变换可以和另一个重合,从而可以确定它们的对应顶点、对应角和对应边.
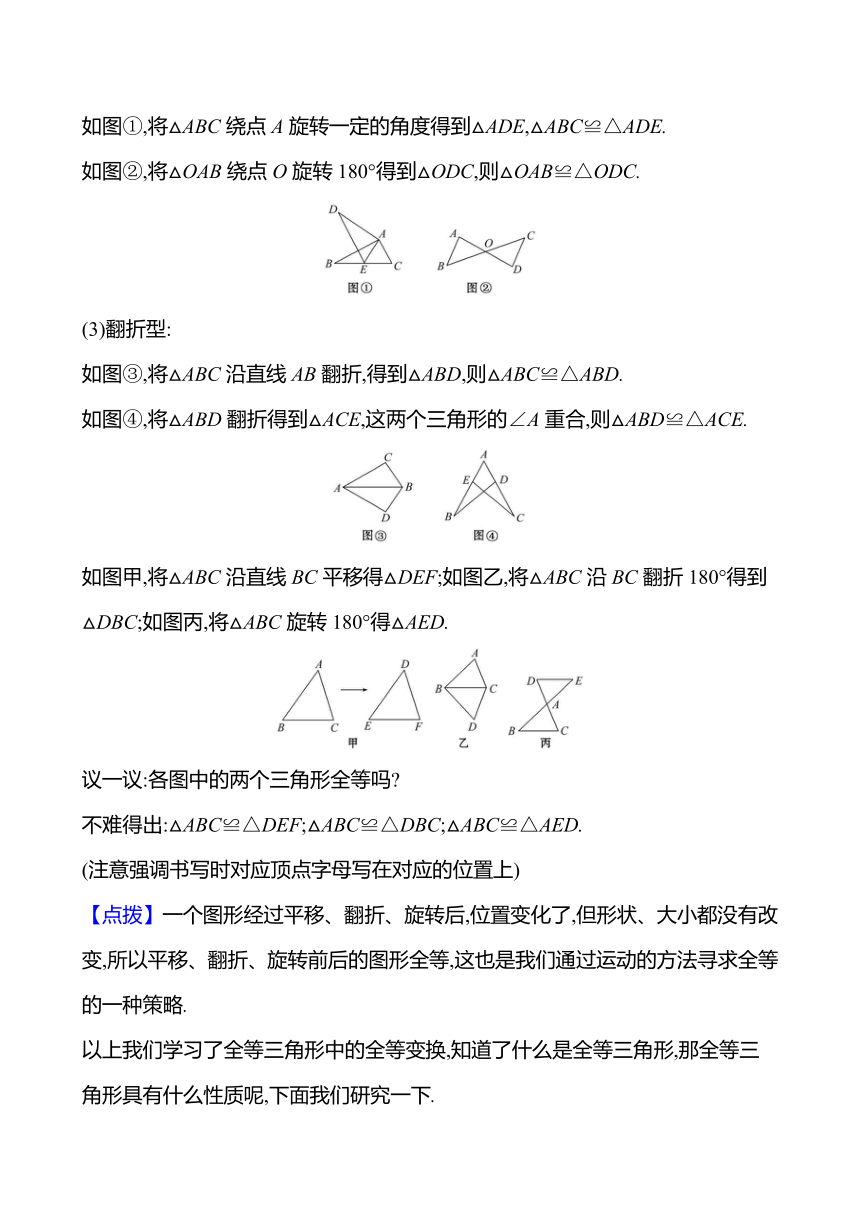
(1)平移型:
如图所示,将△ACE沿直线AC平行移动AB的长度,得到△BDF,△ACE≌△BDF.
(2)旋转型:
如图①,将△ABC绕点A旋转一定的角度得到△ADE,△ABC≌△ADE.
如图②,将△OAB绕点O旋转180°得到△ODC,则△OAB≌△ODC.
(3)翻折型:
如图③,将△ABC沿直线AB翻折,得到△ABD,则△ABC≌△ABD.
如图④,将△ABD翻折得到△ACE,这两个三角形的∠A重合,则△ABD≌△ACE.
如图甲,将△ABC沿直线BC平移得△DEF;如图乙,将△ABC沿BC翻折180°得到△DBC;如图丙,将△ABC旋转180°得△AED.
议一议:各图中的两个三角形全等吗
不难得出:△ABC≌△DEF;△ABC≌△DBC;△ABC≌△AED.
(注意强调书写时对应顶点字母写在对应的位置上)
【点拨】一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略.
以上我们学习了全等三角形中的全等变换,知道了什么是全等三角形,那全等三角形具有什么性质呢,下面我们研究一下.
活动三:探究全等三角形的性质
(1)性质:
全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:∵△ABC≌△DEF,
∴∠A=∠D,∠B=∠E,∠C=∠F
AB=DE,BC=EF,AC=DF.
(2)作用:
运用全等三角形的性质可以证明:两条线段相等、两个角相等.
(3)拓展:
由全等三角形的对应边相等、对应角相等,可以进一步推广到对应中线、角平分线、高相等、全等三角形的周长相等、面积相等,但周长相等的两个三角形不一定全等,面积相等的两个三角形也不一定全等.
【点拨】用全等三角形的性质证明线段或角相等
全等三角形的性质是证明线段或角相等的重要方法,在运用这个性质时,关键是要结合图形或根据表达式中字母的对应位置,灵活地找到对应边或对应角,牢牢抓住“对应”二字.
以上我们学习了全等三角形的性质,知道了应用全等三角形的性质可解决证明线段相等或角相等的方法,那怎样应用这些知识解决问题呢
活动四:应用举例:
【例1】下列图形中是全等形的是________.
解析:上述图形中,(5)和(7)形状相同,但大小不同,(6)和(10)大小、形状都不同;(1)和(9)、(2)和(3)、(11)和(12)尽管方向不同,但大小、形状完全相同,所以它们是全等形,(4)和(8)都是五角星,是全等形.
答案:(1)和(9)、(2)和(3)、(4)和(8)、(11)和(12).
总结:全等图形的识别:
两个图形是否全等只与这两个图形的形状和大小有关,与图形所在的位置无关,只要把它们叠放在一起,看是否重合,重合即为全等形.
【例2】如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
分析:对应边和对应角只能从两个三角形中找,所以需将△ABE和△ACD从复杂的图形中分离出来.
根据位置元素来找:有相等元素,它们就是对应元素,然后再依据已知的对应元素找出其余的对应元素.常用方法有:
(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.
(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
解:对应角为∠BAE和∠CAD.
对应边为AB与AC、AE与AD、BE与CD.
总结:寻找对应边、角的方法:
有公共边的,公共边是对应边;有公共角的,公共角是对应角;有对顶角的,对顶角是对应角.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角.
【例3】如图,△ABC≌△DBE,点D在边AC上,BC与DE相交于点P,已知∠ABE=162°,∠DBC=30°,∠C=27°,求∠BDE的度数.
分析:先求出∠ABD+∠CBE=132°,再根据三角形全等得到∠ABC=∠DBE,∠C=∠E=27°,进而求出∠ABD=∠CBE=132°÷2=66°,∠DBE=∠DBC+∠CBE=96°,最后根据三角形内角和得到答案.
解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=∠ABE-∠DBC=162°-30°=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E=27°,
∴∠ABD=∠CBE=132°÷2=66°,
∴∠DBE=∠DBC+∠CBE=30°+66°=96°,
∴∠BDE=180°-∠DBE-∠E=180°-96°-27°=57°,即∠BDE的度数为57°.
总结:全等三角形的对应边相等,对应角相等.利用全等三角形的性质可证明线段相等或角相等.
三、交流反思
1.通过这节课的学习,掌握全等变换的方法.
2.通过本节课探索出全等三角形的性质.
四、检测反馈
1.如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于 ( )
A.6 B.5
C.4 D.无法确定
2.如图,△ABC≌△AEF,若∠ABC和∠AEF是对应角,则∠EAC等于 ( )
A.∠ACB B.∠CAF
C.∠BAF D.∠BAC
3.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为 ( )
A.40° B.35°
C.30° D.25°
4.如图,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,∠A=25°,∠B=48°;那么DE=________cm,EC=________cm,∠C=________°,∠D=________°.
5.如图,△OCA≌△OBD, C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
6.如图,△ABC≌△ADE,其中C和E,B和D是对应顶点,写出这两个三角形中的对应边和对应角.
7.已知,如图△ABC≌△ADE,试找出对应边、对应角.
五、布置作业
教科书P31习题14.1第2,4,5题.
六、板书设计
第十四章 全等三角形
14.1 全等三角形及其性质
1.全等形的概念 例题板演 学生板演
2.全等三角形的概念
3.全等三角形的性质
4.全等三角形的性质应用
小结:找对应元素的方法
运动法:翻折、旋转、平移.
位置法:对应角→对应边,
对应边→对应角
七、教学反思
本节课的教学过程是:首先,展示教材上的图案以及制作的一些图案,引导学生读图,激发学生兴趣,从图中去发现形状与大小完全相同的图形.然后教师安排学生自己动手随意去作两个形状与大小相同的图形,通过动手实践,合作交流,直观感知全等形和全等三角形的概念.其次,通过阅读法让学生找出全等形和全等三角形的概念.然后,教师随即演示一个三角形经平移,翻折,旋转后构成的两个三角形全等.通过教具演示让学生体会对应顶点、对应边、对应角的概念,并以找朋友的形式练习指出对应顶点、对应边、对应角,加强对对应元素的熟练程度.此时给出全等三角形的表示方法,提示对应顶点,写在对应的位置,然后再给出用全等符号表示全等三角形练习,加强对知识的巩固,再给出练习判断哪一种表示全等三角形的方法正确,通过对图形及文字语言的综合阅读,由此去理解“对应顶点写在对应的位置上”的含义.再次,通过学生对全等三角形纸板的观察,小组讨论,合作交流,观察对应边、对应角有何关系,从而得出全等三角形的性质.并通过练习来理解全等三角形的性质并渗透符号语言推理.最后教师小结,这节课我们知道了什么是全等形、全等三角形,学会了用全等符号表示全等三角形,会用全等三角形的性质解决一些简单的实际问题.
14.1 全等三角形及其性质
【教学目标】
1.知道什么是全等形,全等三角形以及全等三角形对应的元素.
2.能用符号正确地表示两个三角形全等.
3.能够从图形中寻找全等三角形,能熟练地找出两个全等三角形的对应顶点、对应边、对应角.
4.探索并掌握全等三角形的性质,能够利用性质解决简单的问题.
5.经历探索全等三角形性质的过程,能在全等三角形中正确找出对应边、对应角.
【重点难点】
重点:全等三角形以及相关概念.探索全等三角形的性质.
难点:掌握找对应边、对应角的方法.
【教学过程】
一、创设情境,导入新课
[复习旧知]
1.用多媒体展示生活中的大量图形的形状与大小完全相同的图片或录像片断.
2.教师出示演示课件:庐山风景,以诗“横看成岭侧成峰,远近高低各不同,不识庐山真面目,只缘身在此山中”指出大自然中庐山的唯一性,但是我们可以通过摄影把庐山的美景拍下来,可以洗出千万张一模一样的庐山相片.
这种形状与大小完全相同的图形就是全等形,那什么是全等形 全等形具有什么性质 这一节课我们就来学习.
二、探究归纳
活动一:探究全等形的概念
【问题】按照教科书的要求,将一块三角尺按在纸板上,画出图形,按照图形裁下纸板.观察裁下的纸板的形状、大小是否完全一样,能否完全重合
答案:能够完全重合.
1.你还能说一说自己身边还有哪些形状和大小都相同的图形吗
(1)全等形:能够完全重合的两个图形叫作全等形.
(2)全等形的判别方法:
两个图形→即完全重合.
2.全等三角形的定义和表示方法
(1)全等三角形的定义:能够完全重合的两个三角形叫作全等三角形.
全等三角形是特殊的全等形.
(2)对应元素:
把两个全等的三角形重合到一起:
①对应顶点:重合的顶点;
②对应边:重合的边;
③对应角:重合的角.
如图,△ABC与△DEF全等.
对应顶点有:点A和点D,点B和点E,点C和点F;
对应边有:AB和DE,BC和EF,AC和DF.
对应角有:∠A和∠D,∠B和∠E,∠C和∠F.
(3)表示方法:
“全等”用“≌”表示,读作“全等于”.
例如,△ABC与△A'B'C'全等,点A和点A',点B和点B',点C和点C'是对应顶点,记作△ABC≌△A'B'C'.
以上我们学习了全等三角形的概念,知道了什么是全等三角形.下面我们研究一下怎样的图形变换得到全等三角形.
活动二:全等三角形中的全等变换
【问题】只改变图形的位置,而不改变其形状、大小的变换,叫作全等变换.平移、翻折、旋转都属于全等变换.
一个三角形经过全等变换,位置发生了变化,但其形状、大小未发生变化.通过观察两个全等三角形中的一个经过怎样的全等变换可以和另一个重合,从而可以确定它们的对应顶点、对应角和对应边.
(1)平移型:
如图所示,将△ACE沿直线AC平行移动AB的长度,得到△BDF,△ACE≌△BDF.
(2)旋转型:
如图①,将△ABC绕点A旋转一定的角度得到△ADE,△ABC≌△ADE.
如图②,将△OAB绕点O旋转180°得到△ODC,则△OAB≌△ODC.
(3)翻折型:
如图③,将△ABC沿直线AB翻折,得到△ABD,则△ABC≌△ABD.
如图④,将△ABD翻折得到△ACE,这两个三角形的∠A重合,则△ABD≌△ACE.
如图甲,将△ABC沿直线BC平移得△DEF;如图乙,将△ABC沿BC翻折180°得到△DBC;如图丙,将△ABC旋转180°得△AED.
议一议:各图中的两个三角形全等吗
不难得出:△ABC≌△DEF;△ABC≌△DBC;△ABC≌△AED.
(注意强调书写时对应顶点字母写在对应的位置上)
【点拨】一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略.
以上我们学习了全等三角形中的全等变换,知道了什么是全等三角形,那全等三角形具有什么性质呢,下面我们研究一下.
活动三:探究全等三角形的性质
(1)性质:
全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:∵△ABC≌△DEF,
∴∠A=∠D,∠B=∠E,∠C=∠F
AB=DE,BC=EF,AC=DF.
(2)作用:
运用全等三角形的性质可以证明:两条线段相等、两个角相等.
(3)拓展:
由全等三角形的对应边相等、对应角相等,可以进一步推广到对应中线、角平分线、高相等、全等三角形的周长相等、面积相等,但周长相等的两个三角形不一定全等,面积相等的两个三角形也不一定全等.
【点拨】用全等三角形的性质证明线段或角相等
全等三角形的性质是证明线段或角相等的重要方法,在运用这个性质时,关键是要结合图形或根据表达式中字母的对应位置,灵活地找到对应边或对应角,牢牢抓住“对应”二字.
以上我们学习了全等三角形的性质,知道了应用全等三角形的性质可解决证明线段相等或角相等的方法,那怎样应用这些知识解决问题呢
活动四:应用举例:
【例1】下列图形中是全等形的是________.
解析:上述图形中,(5)和(7)形状相同,但大小不同,(6)和(10)大小、形状都不同;(1)和(9)、(2)和(3)、(11)和(12)尽管方向不同,但大小、形状完全相同,所以它们是全等形,(4)和(8)都是五角星,是全等形.
答案:(1)和(9)、(2)和(3)、(4)和(8)、(11)和(12).
总结:全等图形的识别:
两个图形是否全等只与这两个图形的形状和大小有关,与图形所在的位置无关,只要把它们叠放在一起,看是否重合,重合即为全等形.
【例2】如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.
分析:对应边和对应角只能从两个三角形中找,所以需将△ABE和△ACD从复杂的图形中分离出来.
根据位置元素来找:有相等元素,它们就是对应元素,然后再依据已知的对应元素找出其余的对应元素.常用方法有:
(1)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.
(2)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.
解:对应角为∠BAE和∠CAD.
对应边为AB与AC、AE与AD、BE与CD.
总结:寻找对应边、角的方法:
有公共边的,公共边是对应边;有公共角的,公共角是对应角;有对顶角的,对顶角是对应角.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角.
【例3】如图,△ABC≌△DBE,点D在边AC上,BC与DE相交于点P,已知∠ABE=162°,∠DBC=30°,∠C=27°,求∠BDE的度数.
分析:先求出∠ABD+∠CBE=132°,再根据三角形全等得到∠ABC=∠DBE,∠C=∠E=27°,进而求出∠ABD=∠CBE=132°÷2=66°,∠DBE=∠DBC+∠CBE=96°,最后根据三角形内角和得到答案.
解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=∠ABE-∠DBC=162°-30°=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E=27°,
∴∠ABD=∠CBE=132°÷2=66°,
∴∠DBE=∠DBC+∠CBE=30°+66°=96°,
∴∠BDE=180°-∠DBE-∠E=180°-96°-27°=57°,即∠BDE的度数为57°.
总结:全等三角形的对应边相等,对应角相等.利用全等三角形的性质可证明线段相等或角相等.
三、交流反思
1.通过这节课的学习,掌握全等变换的方法.
2.通过本节课探索出全等三角形的性质.
四、检测反馈
1.如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于 ( )
A.6 B.5
C.4 D.无法确定
2.如图,△ABC≌△AEF,若∠ABC和∠AEF是对应角,则∠EAC等于 ( )
A.∠ACB B.∠CAF
C.∠BAF D.∠BAC
3.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为 ( )
A.40° B.35°
C.30° D.25°
4.如图,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,∠A=25°,∠B=48°;那么DE=________cm,EC=________cm,∠C=________°,∠D=________°.
5.如图,△OCA≌△OBD, C和B,A和D是对应顶点,说出这两个三角形中相等的边和角.
6.如图,△ABC≌△ADE,其中C和E,B和D是对应顶点,写出这两个三角形中的对应边和对应角.
7.已知,如图△ABC≌△ADE,试找出对应边、对应角.
五、布置作业
教科书P31习题14.1第2,4,5题.
六、板书设计
第十四章 全等三角形
14.1 全等三角形及其性质
1.全等形的概念 例题板演 学生板演
2.全等三角形的概念
3.全等三角形的性质
4.全等三角形的性质应用
小结:找对应元素的方法
运动法:翻折、旋转、平移.
位置法:对应角→对应边,
对应边→对应角
七、教学反思
本节课的教学过程是:首先,展示教材上的图案以及制作的一些图案,引导学生读图,激发学生兴趣,从图中去发现形状与大小完全相同的图形.然后教师安排学生自己动手随意去作两个形状与大小相同的图形,通过动手实践,合作交流,直观感知全等形和全等三角形的概念.其次,通过阅读法让学生找出全等形和全等三角形的概念.然后,教师随即演示一个三角形经平移,翻折,旋转后构成的两个三角形全等.通过教具演示让学生体会对应顶点、对应边、对应角的概念,并以找朋友的形式练习指出对应顶点、对应边、对应角,加强对对应元素的熟练程度.此时给出全等三角形的表示方法,提示对应顶点,写在对应的位置,然后再给出用全等符号表示全等三角形练习,加强对知识的巩固,再给出练习判断哪一种表示全等三角形的方法正确,通过对图形及文字语言的综合阅读,由此去理解“对应顶点写在对应的位置上”的含义.再次,通过学生对全等三角形纸板的观察,小组讨论,合作交流,观察对应边、对应角有何关系,从而得出全等三角形的性质.并通过练习来理解全等三角形的性质并渗透符号语言推理.最后教师小结,这节课我们知道了什么是全等形、全等三角形,学会了用全等符号表示全等三角形,会用全等三角形的性质解决一些简单的实际问题.
同课章节目录
