河北省唐山市2024-2025学年七年级下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 河北省唐山市2024-2025学年七年级下学期期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 10:08:56 | ||
图片预览



文档简介
河北省唐山市2024-2025学年下学期七年级期末考试数学试卷
一、单选题
1.如图,同一平面内,直线 m和直线n 的位置关系是( )
A.相交 B.垂直 C.平行 D.重合
2.若,则,其中应该填入的符号是( )
A. B. C. D.
3.面积为49的正方形,其边长为( )
A. B.7 C. D.28
4.在平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,一个玩具汽车赛道,则的度数是( )
A. B. C. D.
6.如图,数轴上表示的解集是( )
A. B. C. D.
7.下列各组数满足方程的是( )
A. B. C. D.
8.若取2.236,计算的结果是( )
A. B.223.6 C. D.
9.若方程中是的3倍,则( )
A. B. C. D.2
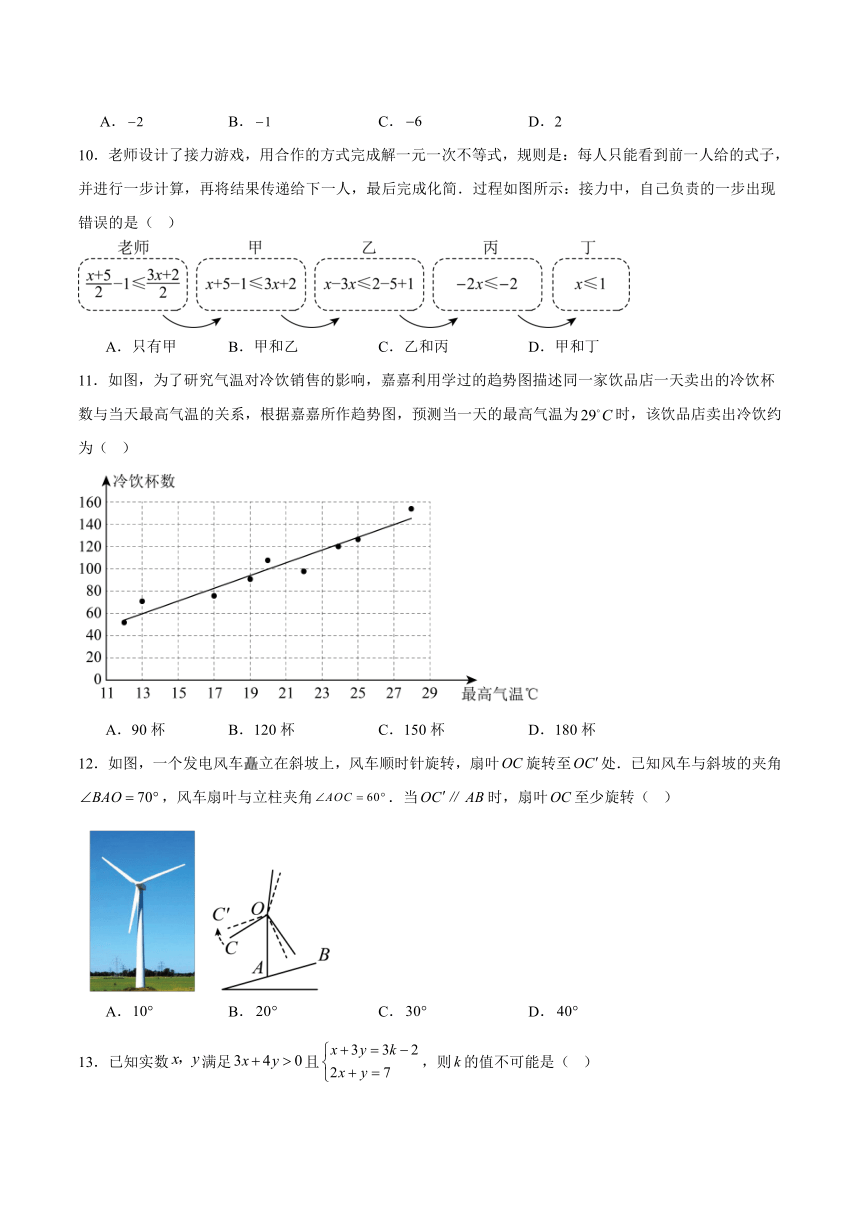
10.老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:接力中,自己负责的一步出现错误的是( )
A.只有甲 B.甲和乙 C.乙和丙 D.甲和丁
11.如图,为了研究气温对冷饮销售的影响,嘉嘉利用学过的趋势图描述同一家饮品店一天卖出的冷饮杯数与当天最高气温的关系,根据嘉嘉所作趋势图,预测当一天的最高气温为时,该饮品店卖出冷饮约为( )
A.90杯 B.120杯 C.150杯 D.180杯
12.如图,一个发电风车矗立在斜坡上,风车顺时针旋转,扇叶旋转至处.已知风车与斜坡的夹角,风车扇叶与立柱夹角.当时,扇叶至少旋转( )
A. B. C. D.
13.已知实数满足且,则的值不可能是( )
A. B. C.0 D.1
14.为进行豌豆种子发芽实验,现将240个豌豆分成4组,放在四个盘子中.每个盘中豌豆的数量都是奇数,其中一个盘中豌豆的数量少,另外三个盘中豌豆的数量多且数量相同.问:应该如何分?设豌豆数量多的三个盘中均有个,则正确的是( )
A.依题意豌豆数量少的盘中有个
B.依题意
C.有最小值,也有最大值
D.是正确解,也是唯一解
二、填空题
15.用不等式表示“为负数”: .
16.已知,且为正整数,则的值可以是 (写出一个即可).
17.如图,已知,点在直线上,点,在直线上,.在线段上任取一点(不与点重合),过点作的垂线交于点.若,则的度数为 .
18.如图,是由5个边长为1的小正方形组成的图形,嘉嘉将图1所示的纸片通过裁剪拼接成了一个大正方形(如图2).
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
(1)大正方形的边长为 ;
(2)嘉嘉借助平面直角坐标系进一步探究大正方形的边长,如图3,以点为原点,以小正方形的边长为单位长度,建立如图所示的坐标系,则点的坐标是 .
三、解答题
19.计算:
(1);
(2).
20.已知不等式组:.
(1)求不等式组的解集并将解集表示在数轴上;
(2)直接写出满足这个不等式组的所有偶数解.
21.已知整式.
(1)若,则,用含的代数式表示;
(2)若,则;若,则,求和的值.
22.在作业纸上,,点在之间,要得知两相交直线所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如表1和表2)
方案I ①分别测量和; ②计算出的大小即可. 方案II ①延伸交于点; ②测量的大小即可.
表1 表2
请根据上述信息解答问题:
(1)对于方案I、II,说法正确的是___________;
A.I可行,II不可行 B.I不可行,II可行
C.I、II都可行 D.I、II都不可行
(2)请选择一种你认为正确的方案说明理由.
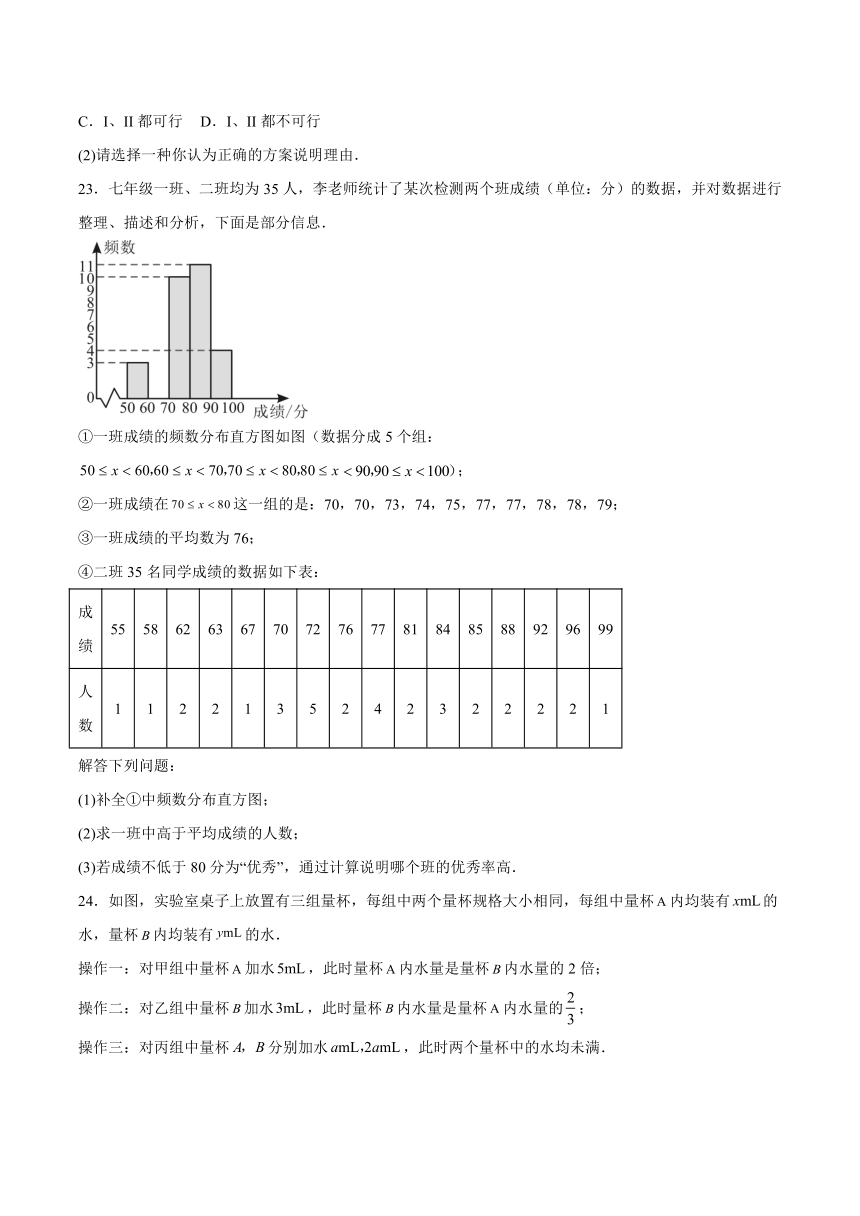
23.七年级一班、二班均为35人,李老师统计了某次检测两个班成绩(单位:分)的数据,并对数据进行整理、描述和分析,下面是部分信息.
①一班成绩的频数分布直方图如图(数据分成5个组:;
②一班成绩在这一组的是:70,70,73,74,75,77,77,78,78,79;
③一班成绩的平均数为76;
④二班35名同学成绩的数据如下表:
成绩 55 58 62 63 67 70 72 76 77 81 84 85 88 92 96 99
人数 1 1 2 2 1 3 5 2 4 2 3 2 2 2 2 1
解答下列问题:
(1)补全①中频数分布直方图;
(2)求一班中高于平均成绩的人数;
(3)若成绩不低于80分为“优秀”,通过计算说明哪个班的优秀率高.
24.如图,实验室桌子上放置有三组量杯,每组中两个量杯规格大小相同,每组中量杯内均装有的水,量杯内均装有的水.
操作一:对甲组中量杯加水,此时量杯内水量是量杯内水量的2倍;
操作二:对乙组中量杯加水,此时量杯内水量是量杯内水量的;
操作三:对丙组中量杯分别加水,此时两个量杯中的水均未满.
(1)求和的值;
(2)操作三中,当量杯中水量比量杯中水量多时,求的最小整数值.
25.在平面直角坐标系中,已知点,将其先向右平移个单位长度,再向上平移个单位长度得到点,则称是点的平移美点.
(1)直接写出点的平移美点;
(2)若点的平移美点在轴上,求的值;
(3)如图,正方形,点,,,,已知点是点的平移美点.
①若点的平移美点为,确定点的坐标;
②将点向上平移个单位长度得到,若线段上的所有点(含端点)都在正方形的边上或内部,直接写出的最大值及此时的值.
参考答案
1.A
解:由图可得:同一平面内,直线 m和直线n 的位置关系是相交,
故选:A.
2.C
解:,
两边同时乘以 (负数),不等号方向改变,得: .
因此,中应填入符号“”,
故选C.
3.B
解:已知面积为49,设边长为,则,
解方程得,
算术平方根为非负数,故,
选项中只有B(7)符合实际意义(边长为正数),
故选:B.
4.D
解:在平面直角坐标系中,第一象限点的坐标符号为,第二象限为,第三象限为,第四象限为,
点的横坐标,纵坐标,符合第四象限的坐标特征,
因此点在第四象限,
故选D.
5.B
解:∵,
∴,
∵,
∴.
故选:B.
6.D
解:∵5处是实心圆点,且折线向左,
∴这个不等式的解集是.
故选D.
7.D
解:当时,方程左边方程右边,故A不符合题意;
当时,方程左边方程右边,故B不符合题意;
当时,方程左边方程右边,故C不符合题意;
当时,方程左边方程右边,故D符合题意;
故选:D.
8.A
解:,
已知,
则
因此结果为,
故选:A.
9.A
将代入方程,得:
解得,
故选A.
10.D
解:,
去分母,得,
故步骤甲错误.
最后一步,系数化为1:得.
故丁步骤错误,
故选:D.
11.C
解:观察统计图可知,随着温度的升高,卖出的冷饮杯数随着气温的升高逐渐呈现上升趋势,
由统计图可知时,冷饮杯数约为140杯,则时,饮品店卖出的冷饮杯数约为150杯,达不到160杯,
故选:C.
12.A
解:∵,,
∴,
∴,
∴扇叶至少旋转.
故选:A.
13.A
解:由方程组
从得,代入:
,
,
把代入 ,得:
,
将 和 代入 ,得:
,
,
,
,
,选项中只有 不满足 ,
故选A.
14.C
解:选项A:错误.数量少的盘子应为,而非.
选项B:错误.由得,即,而选项B中不等式为(即),包含的情况,此时,与题意矛盾.
选项C:正确.由得,即;结合,的取值范围为且为奇数,故有最小值61和最大值79.
选项D:错误.可取61、63、…、79等多个奇数值,并非唯一解.
故选:C.
15.
解:根据题意,得.
故答案为:.
16.1(答案不唯一)
解:∵是整数;
∴是完全平方数;
∴,
∵为正整数,
∴或2或3.
故答案为:1(答案不唯一).
17.
解:如图,
∵,,
∴,
∵,
∴,
∵,
∴,
故答案为:.
18.
解:(1)根据题意得,大正方形的边长为:,
故答案为:;
(2)∵以点为原点,以小正方形的边长为单位长度,
∴由图得点A在第二象限,且边长为,
∴点的坐标是,
故答案为:(1);(2).
19.(1)9
(2)
(1)解:
.
(2)解:
.
20.(1)不等式组的解集为:,数轴表示见解析
(2)偶数解为0和2
(1)解:,
解不等式①得:,
解不等式②:,
所以不等式组的解集为:,
解集表示到数轴上如下:
(2)解:这个不等式组的所有偶数解为0和2.
21.(1);
(2).
(1)解:当时,
,
即,
;
(2)解:分别将;代入得:
解得.
.
22.(1)C;
(2)方案I、II都正确;理由见解析.
(1)解:方案I,如图1:
,
延伸,交于点,
过点作,则,
,
,
,
方案I正确;
方案II,如图2:
,
延伸交于点,
,则,
测量的大小即可,
方案II正确,
综上所述,两种方式都可行,
故选:C;
(2)解:方案I,如图1:
,
延伸,交于点,
过点作,则,
,
,
,
方案I正确;
方案II,如图2:
,
延伸交于点,
,则,
测量的大小即可,
方案II正确;
23.(1)图形见解析;
(2)一班中高于平均成绩的人数为20人;
(3)一班优秀率更高理由见解析.
解:(1)(人),
补全频数分布直方图如下:
(2)在中,超过平均分的人数为5人,
(人),
答:一班中高于平均成绩的人数为20人;
(3)一班:,
二班:,
,
一班优秀率更高.
24.(1)
(2)的最小整数值为15
(1)解:由题意得:,
解得:;
(2)解:由题意得:,
解得:,
则的最小整数值为15.
25.(1);
(2);
(3)①点的坐标为;②的最大值为3,此时的值为0.
(1)解:由题意得点的平移美点为即;
(2)解:点的平移美点的横坐标为,
由题意得,
解得;
(3)解:①∵点的平移美点为,
∴,
解得,
∴点的坐标为;
②∵是平移美点,
∴的横坐标为,纵坐标为,
∵将点向上平移个单位长度得到,
∴,
∵线段的端点需满足: 在正方形内:,;
在正方形内:,;
∴,,
当,且时,最大为3,符合题意;
∴的最大值为3,此时的值为0.
一、单选题
1.如图,同一平面内,直线 m和直线n 的位置关系是( )
A.相交 B.垂直 C.平行 D.重合
2.若,则,其中应该填入的符号是( )
A. B. C. D.
3.面积为49的正方形,其边长为( )
A. B.7 C. D.28
4.在平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,一个玩具汽车赛道,则的度数是( )
A. B. C. D.
6.如图,数轴上表示的解集是( )
A. B. C. D.
7.下列各组数满足方程的是( )
A. B. C. D.
8.若取2.236,计算的结果是( )
A. B.223.6 C. D.
9.若方程中是的3倍,则( )
A. B. C. D.2
10.老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:接力中,自己负责的一步出现错误的是( )
A.只有甲 B.甲和乙 C.乙和丙 D.甲和丁
11.如图,为了研究气温对冷饮销售的影响,嘉嘉利用学过的趋势图描述同一家饮品店一天卖出的冷饮杯数与当天最高气温的关系,根据嘉嘉所作趋势图,预测当一天的最高气温为时,该饮品店卖出冷饮约为( )
A.90杯 B.120杯 C.150杯 D.180杯
12.如图,一个发电风车矗立在斜坡上,风车顺时针旋转,扇叶旋转至处.已知风车与斜坡的夹角,风车扇叶与立柱夹角.当时,扇叶至少旋转( )
A. B. C. D.
13.已知实数满足且,则的值不可能是( )
A. B. C.0 D.1
14.为进行豌豆种子发芽实验,现将240个豌豆分成4组,放在四个盘子中.每个盘中豌豆的数量都是奇数,其中一个盘中豌豆的数量少,另外三个盘中豌豆的数量多且数量相同.问:应该如何分?设豌豆数量多的三个盘中均有个,则正确的是( )
A.依题意豌豆数量少的盘中有个
B.依题意
C.有最小值,也有最大值
D.是正确解,也是唯一解
二、填空题
15.用不等式表示“为负数”: .
16.已知,且为正整数,则的值可以是 (写出一个即可).
17.如图,已知,点在直线上,点,在直线上,.在线段上任取一点(不与点重合),过点作的垂线交于点.若,则的度数为 .
18.如图,是由5个边长为1的小正方形组成的图形,嘉嘉将图1所示的纸片通过裁剪拼接成了一个大正方形(如图2).
(说明:纸片不折叠,拼接不重叠无缝隙无剩余)
(1)大正方形的边长为 ;
(2)嘉嘉借助平面直角坐标系进一步探究大正方形的边长,如图3,以点为原点,以小正方形的边长为单位长度,建立如图所示的坐标系,则点的坐标是 .
三、解答题
19.计算:
(1);
(2).
20.已知不等式组:.
(1)求不等式组的解集并将解集表示在数轴上;
(2)直接写出满足这个不等式组的所有偶数解.
21.已知整式.
(1)若,则,用含的代数式表示;
(2)若,则;若,则,求和的值.
22.在作业纸上,,点在之间,要得知两相交直线所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如表1和表2)
方案I ①分别测量和; ②计算出的大小即可. 方案II ①延伸交于点; ②测量的大小即可.
表1 表2
请根据上述信息解答问题:
(1)对于方案I、II,说法正确的是___________;
A.I可行,II不可行 B.I不可行,II可行
C.I、II都可行 D.I、II都不可行
(2)请选择一种你认为正确的方案说明理由.
23.七年级一班、二班均为35人,李老师统计了某次检测两个班成绩(单位:分)的数据,并对数据进行整理、描述和分析,下面是部分信息.
①一班成绩的频数分布直方图如图(数据分成5个组:;
②一班成绩在这一组的是:70,70,73,74,75,77,77,78,78,79;
③一班成绩的平均数为76;
④二班35名同学成绩的数据如下表:
成绩 55 58 62 63 67 70 72 76 77 81 84 85 88 92 96 99
人数 1 1 2 2 1 3 5 2 4 2 3 2 2 2 2 1
解答下列问题:
(1)补全①中频数分布直方图;
(2)求一班中高于平均成绩的人数;
(3)若成绩不低于80分为“优秀”,通过计算说明哪个班的优秀率高.
24.如图,实验室桌子上放置有三组量杯,每组中两个量杯规格大小相同,每组中量杯内均装有的水,量杯内均装有的水.
操作一:对甲组中量杯加水,此时量杯内水量是量杯内水量的2倍;
操作二:对乙组中量杯加水,此时量杯内水量是量杯内水量的;
操作三:对丙组中量杯分别加水,此时两个量杯中的水均未满.
(1)求和的值;
(2)操作三中,当量杯中水量比量杯中水量多时,求的最小整数值.
25.在平面直角坐标系中,已知点,将其先向右平移个单位长度,再向上平移个单位长度得到点,则称是点的平移美点.
(1)直接写出点的平移美点;
(2)若点的平移美点在轴上,求的值;
(3)如图,正方形,点,,,,已知点是点的平移美点.
①若点的平移美点为,确定点的坐标;
②将点向上平移个单位长度得到,若线段上的所有点(含端点)都在正方形的边上或内部,直接写出的最大值及此时的值.
参考答案
1.A
解:由图可得:同一平面内,直线 m和直线n 的位置关系是相交,
故选:A.
2.C
解:,
两边同时乘以 (负数),不等号方向改变,得: .
因此,中应填入符号“”,
故选C.
3.B
解:已知面积为49,设边长为,则,
解方程得,
算术平方根为非负数,故,
选项中只有B(7)符合实际意义(边长为正数),
故选:B.
4.D
解:在平面直角坐标系中,第一象限点的坐标符号为,第二象限为,第三象限为,第四象限为,
点的横坐标,纵坐标,符合第四象限的坐标特征,
因此点在第四象限,
故选D.
5.B
解:∵,
∴,
∵,
∴.
故选:B.
6.D
解:∵5处是实心圆点,且折线向左,
∴这个不等式的解集是.
故选D.
7.D
解:当时,方程左边方程右边,故A不符合题意;
当时,方程左边方程右边,故B不符合题意;
当时,方程左边方程右边,故C不符合题意;
当时,方程左边方程右边,故D符合题意;
故选:D.
8.A
解:,
已知,
则
因此结果为,
故选:A.
9.A
将代入方程,得:
解得,
故选A.
10.D
解:,
去分母,得,
故步骤甲错误.
最后一步,系数化为1:得.
故丁步骤错误,
故选:D.
11.C
解:观察统计图可知,随着温度的升高,卖出的冷饮杯数随着气温的升高逐渐呈现上升趋势,
由统计图可知时,冷饮杯数约为140杯,则时,饮品店卖出的冷饮杯数约为150杯,达不到160杯,
故选:C.
12.A
解:∵,,
∴,
∴,
∴扇叶至少旋转.
故选:A.
13.A
解:由方程组
从得,代入:
,
,
把代入 ,得:
,
将 和 代入 ,得:
,
,
,
,
,选项中只有 不满足 ,
故选A.
14.C
解:选项A:错误.数量少的盘子应为,而非.
选项B:错误.由得,即,而选项B中不等式为(即),包含的情况,此时,与题意矛盾.
选项C:正确.由得,即;结合,的取值范围为且为奇数,故有最小值61和最大值79.
选项D:错误.可取61、63、…、79等多个奇数值,并非唯一解.
故选:C.
15.
解:根据题意,得.
故答案为:.
16.1(答案不唯一)
解:∵是整数;
∴是完全平方数;
∴,
∵为正整数,
∴或2或3.
故答案为:1(答案不唯一).
17.
解:如图,
∵,,
∴,
∵,
∴,
∵,
∴,
故答案为:.
18.
解:(1)根据题意得,大正方形的边长为:,
故答案为:;
(2)∵以点为原点,以小正方形的边长为单位长度,
∴由图得点A在第二象限,且边长为,
∴点的坐标是,
故答案为:(1);(2).
19.(1)9
(2)
(1)解:
.
(2)解:
.
20.(1)不等式组的解集为:,数轴表示见解析
(2)偶数解为0和2
(1)解:,
解不等式①得:,
解不等式②:,
所以不等式组的解集为:,
解集表示到数轴上如下:
(2)解:这个不等式组的所有偶数解为0和2.
21.(1);
(2).
(1)解:当时,
,
即,
;
(2)解:分别将;代入得:
解得.
.
22.(1)C;
(2)方案I、II都正确;理由见解析.
(1)解:方案I,如图1:
,
延伸,交于点,
过点作,则,
,
,
,
方案I正确;
方案II,如图2:
,
延伸交于点,
,则,
测量的大小即可,
方案II正确,
综上所述,两种方式都可行,
故选:C;
(2)解:方案I,如图1:
,
延伸,交于点,
过点作,则,
,
,
,
方案I正确;
方案II,如图2:
,
延伸交于点,
,则,
测量的大小即可,
方案II正确;
23.(1)图形见解析;
(2)一班中高于平均成绩的人数为20人;
(3)一班优秀率更高理由见解析.
解:(1)(人),
补全频数分布直方图如下:
(2)在中,超过平均分的人数为5人,
(人),
答:一班中高于平均成绩的人数为20人;
(3)一班:,
二班:,
,
一班优秀率更高.
24.(1)
(2)的最小整数值为15
(1)解:由题意得:,
解得:;
(2)解:由题意得:,
解得:,
则的最小整数值为15.
25.(1);
(2);
(3)①点的坐标为;②的最大值为3,此时的值为0.
(1)解:由题意得点的平移美点为即;
(2)解:点的平移美点的横坐标为,
由题意得,
解得;
(3)解:①∵点的平移美点为,
∴,
解得,
∴点的坐标为;
②∵是平移美点,
∴的横坐标为,纵坐标为,
∵将点向上平移个单位长度得到,
∴,
∵线段的端点需满足: 在正方形内:,;
在正方形内:,;
∴,,
当,且时,最大为3,符合题意;
∴的最大值为3,此时的值为0.
同课章节目录
