北师大版四年级下册数学2.4探索与发现:三角形边的关系(课件)(共17张PPT)
文档属性
| 名称 | 北师大版四年级下册数学2.4探索与发现:三角形边的关系(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 904.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 18:28:53 | ||
图片预览




文档简介
(共17张PPT)
第二单元 认识三角形和四边形
三角形边的关系
北师大版 数学 四年级下册
是不是只要有3条线段就能摆成三角形?
导入
3
5
6
3
4
6
3
3
6
3
2
6
(1)
(3)
(2)
(4)
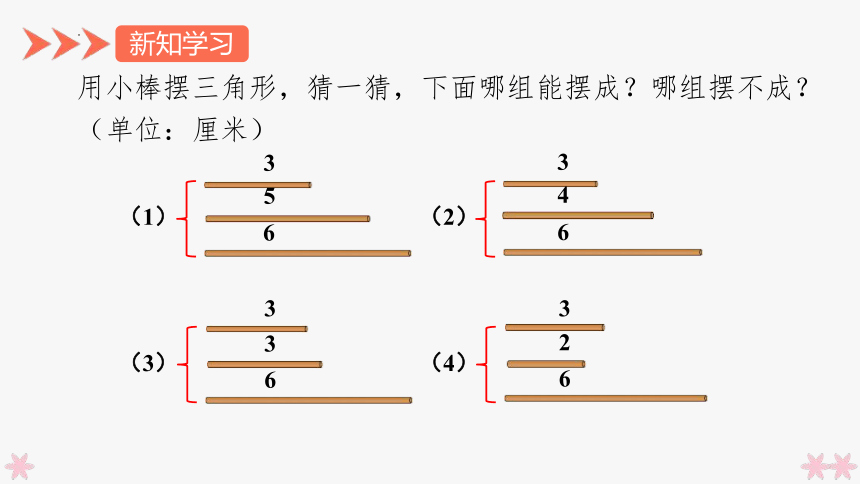
用小棒摆三角形,猜一猜,下面哪组能摆成?哪组摆不成?(单位:厘米)
新知学习
1.用小棒试着摆一摆,记下能摆成的组小棒的长度。
2.在小组内交流讨论,能摆成三角形的小棒,有什
么关系。
3.想一想怎样的3根小棒能摆成一个三角形?请组内
交流总结。
小组合作
5
6
(1)
3
3
4
6
(2)
3
3
6
(3)
3
2
6
(4)
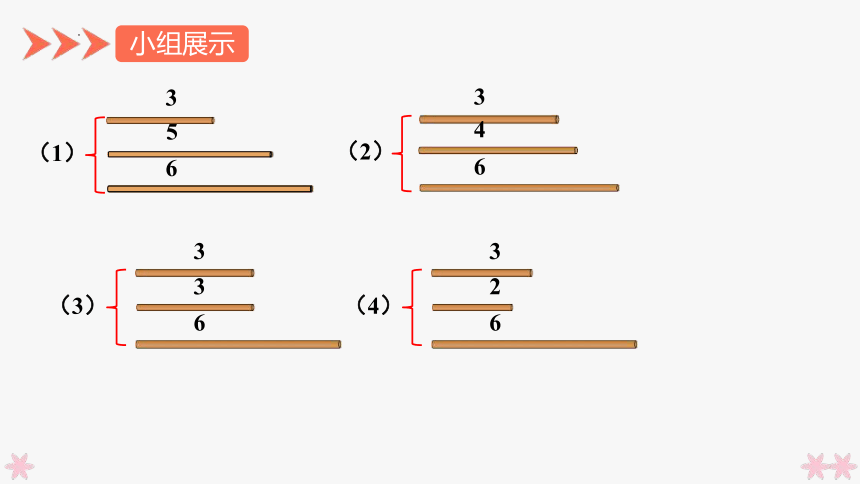
小组展示
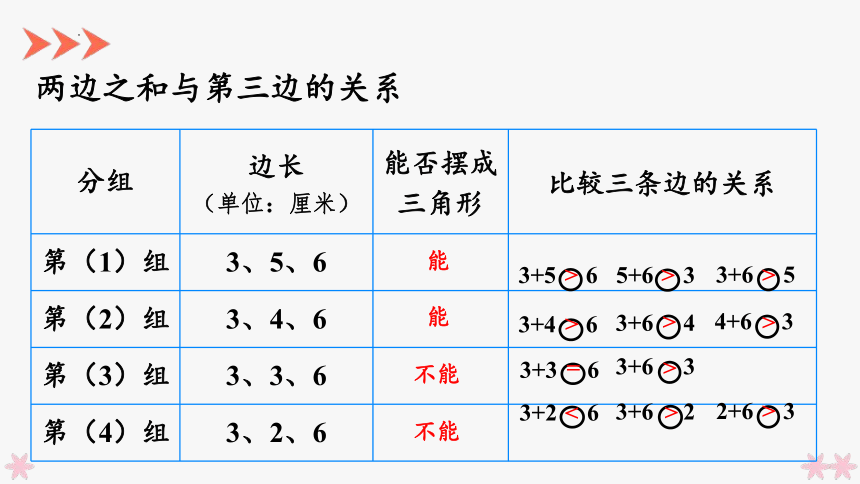
两边之和与第三边的关系
分组 边长 (单位:厘米) 能否摆成三角形 比较三条边的关系
第(1)组 3、5、6
第(2)组 3、4、6
第(3)组 3、3、6
第(4)组 3、2、6
能
能
不能
不能
3+5 6
3+6 5
5+6 3
3+4 6
4+6 3
3+6 4
3+3 6
3+6 3
3+2 6
2+6 3
3+6 2
>
>
>
>
>
>
=
>
<
>
>
第(1)组小棒和第(2)组小棒中任意两根小棒的长度之和大于第三根小棒的长度。
第(3)组小棒和第(4)组小棒中不符合任意两根小棒的长度之和大于第三根小棒的长度。
三角形任意两边之和大于第三边。
知识小结
学以致用
下面哪三条线段可以围成三角形
12,5,7
3,4,5
4,6,1
三角形任意两边之和大于第三边。
12+5>7
12+7>5
5+7=12
3+4>5
3+5>4
4+5>3
4+6>1
4+1<6
×
√
×
1.在能摆成三角形的小棒下面画“√”。
(单位:厘米)
√
√
练一练
2.从下面5根小棒中任意取出3根,摆出两种不同的
三角形。(单位:厘米)
3
4
6
3
3
3
4
6
3
3
3
等边三角形
钝角三角形
3.当一个三角形的两条边分别长5厘米、8厘米时,第三条边长度可能是( )
A.3厘米 B.13厘米 C.12厘米
C
三角形任意两边之和大于第三边
5,8,
5,8,3
5,8,13
5,8,12
5+3=8 ×
5+8=13 ×
4.用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
能
等边
不能
能
等腰
能
等边
三角形任意两边之差小于第三边
三角形任意两边之差与第三边会有关系吗?
√
√
4-3=1
6-3=3
6-4=2
6
4
3
<
<
<
7-5=2
11-5=6
11-7=4
11
7
3
<
<
<
2-1=1
3-2=1
3-1=2
3
1
2
<
=
=
5.判断
(1)三角形最长的一条边有可能大于其他两边的和。
(2)三角形中任意两边之差小于第三边。
(3)用同样长的小棒不能围成三角形。
(4)在三角形中,有两条边都为4厘米,那么第三 条边一定大于4厘米。
4,4,
第三边
<
<
两边之差
两边之和
4-4=0
4+4=8
×
√
×
×
多学一点
下面哪三条线段可以围成三角形
12,5,7
3,4,5
4,6,1
×
√
×
除了按照“任意两边之和大于第三边”或“任意两边之差小于第三边”判断能否围成三角形
还可以根据“三角形最短的两边之和大于最长边”来判断,即“短边之和大于第三边”
也可以根据“三角形最长的两边之差小于最短边”来判断,即“长边之差小于第三边”
三角形边的关系
知识再现
任意两边之和大于第三边
任意两边之差小于第三边
短边之和大于第三边
长边之差小于第三边
两边之差<第三边<两边之和
完成练习册
作业
第二单元 认识三角形和四边形
三角形边的关系
北师大版 数学 四年级下册
是不是只要有3条线段就能摆成三角形?
导入
3
5
6
3
4
6
3
3
6
3
2
6
(1)
(3)
(2)
(4)
用小棒摆三角形,猜一猜,下面哪组能摆成?哪组摆不成?(单位:厘米)
新知学习
1.用小棒试着摆一摆,记下能摆成的组小棒的长度。
2.在小组内交流讨论,能摆成三角形的小棒,有什
么关系。
3.想一想怎样的3根小棒能摆成一个三角形?请组内
交流总结。
小组合作
5
6
(1)
3
3
4
6
(2)
3
3
6
(3)
3
2
6
(4)
小组展示
两边之和与第三边的关系
分组 边长 (单位:厘米) 能否摆成三角形 比较三条边的关系
第(1)组 3、5、6
第(2)组 3、4、6
第(3)组 3、3、6
第(4)组 3、2、6
能
能
不能
不能
3+5 6
3+6 5
5+6 3
3+4 6
4+6 3
3+6 4
3+3 6
3+6 3
3+2 6
2+6 3
3+6 2
>
>
>
>
>
>
=
>
<
>
>
第(1)组小棒和第(2)组小棒中任意两根小棒的长度之和大于第三根小棒的长度。
第(3)组小棒和第(4)组小棒中不符合任意两根小棒的长度之和大于第三根小棒的长度。
三角形任意两边之和大于第三边。
知识小结
学以致用
下面哪三条线段可以围成三角形
12,5,7
3,4,5
4,6,1
三角形任意两边之和大于第三边。
12+5>7
12+7>5
5+7=12
3+4>5
3+5>4
4+5>3
4+6>1
4+1<6
×
√
×
1.在能摆成三角形的小棒下面画“√”。
(单位:厘米)
√
√
练一练
2.从下面5根小棒中任意取出3根,摆出两种不同的
三角形。(单位:厘米)
3
4
6
3
3
3
4
6
3
3
3
等边三角形
钝角三角形
3.当一个三角形的两条边分别长5厘米、8厘米时,第三条边长度可能是( )
A.3厘米 B.13厘米 C.12厘米
C
三角形任意两边之和大于第三边
5,8,
5,8,3
5,8,13
5,8,12
5+3=8 ×
5+8=13 ×
4.用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
能
等边
不能
能
等腰
能
等边
三角形任意两边之差小于第三边
三角形任意两边之差与第三边会有关系吗?
√
√
4-3=1
6-3=3
6-4=2
6
4
3
<
<
<
7-5=2
11-5=6
11-7=4
11
7
3
<
<
<
2-1=1
3-2=1
3-1=2
3
1
2
<
=
=
5.判断
(1)三角形最长的一条边有可能大于其他两边的和。
(2)三角形中任意两边之差小于第三边。
(3)用同样长的小棒不能围成三角形。
(4)在三角形中,有两条边都为4厘米,那么第三 条边一定大于4厘米。
4,4,
第三边
<
<
两边之差
两边之和
4-4=0
4+4=8
×
√
×
×
多学一点
下面哪三条线段可以围成三角形
12,5,7
3,4,5
4,6,1
×
√
×
除了按照“任意两边之和大于第三边”或“任意两边之差小于第三边”判断能否围成三角形
还可以根据“三角形最短的两边之和大于最长边”来判断,即“短边之和大于第三边”
也可以根据“三角形最长的两边之差小于最短边”来判断,即“长边之差小于第三边”
三角形边的关系
知识再现
任意两边之和大于第三边
任意两边之差小于第三边
短边之和大于第三边
长边之差小于第三边
两边之差<第三边<两边之和
完成练习册
作业
