1.1 等腰三角形(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学八年级下册
文档属性
| 名称 | 1.1 等腰三角形(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 348.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 12:38:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1 等腰三角形
一.选择题(共10小题)
1.如图,在△ABC中,D是边AB上一点,AD=CD=BC,∠A=25°,则∠BCD的度数为( )
A.50° B.65° C.80° D.105°
2.等腰三角形的两边分别为5和10,则它的周长是( )
A.20 B.15 C.25 D.20或25
3.如图,△ABC是等边三角形,点D在BC的延长线上,点E是AC的中点,连接DE并延长交AB于点F,且CE=CD,若EF=2,则DF的长为( )
A.3 B.4 C.6 D.8
4.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
5.已知等腰三角形的两边长分别是5和6,则第三边的长是( )
A.5 B.6 C.5或6 D.10
6.如图,在△ABC中,∠BAC=90°,AC=6,AB=8,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,则DE的长为( )
A.14 B.16 C.18 D.20
7.牛顿曾说过:反证法是数学家最精良的武器之一,我们用反证法证明命题“三角形中不能两个直角”,应先假设( )
A.三角形中有一个内角是直角
B.三角形中有两个内角是直角
C.三角形中有三个内角是直角
D.三角形中不能有内角是直角
8.如图,M,N为4×4方格纸中格点上的两点,若以MN为边,在方格中取一点P(P在格点上),使得△MNP为等腰三角形,则点P的个数为( )
A.3个 B.4个 C.5个 D.6个
9.已知等腰△ABC,AD为BC边上的高,且,则等腰△ABC的底角的度数为( )
A.45° B.75°或60°
C.45°或75° D.以上都不对
10.如图,△ABC中,∠B=∠C,AD为BC边上的高,下列结论中不正确的是( )
A.AB=AC B.AD=BC C.BD=CD D.∠BAD=∠CAD
二.填空题(共6小题)
11.用反证法证明,“在△ABC中,∠A、∠B对边是a、b,若∠A>∠B,则a>b.”第一步应假设 .
12.如图,等边△ABC 的边长为4cm,P、Q两点分别从A、B两点同时出发,点P以8cm/s的速度按顺时针方向在等边△ABC的边上运动,点Q以2cm/s的速度按逆时针方向在等边△ABC的边上运动,则P、Q两点第一次在等边△ABC 顶点处相遇的时间t1= 秒,第四次在等边△ABC顶点处相遇的时间t4= 秒.
13.如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上(均不与点A、B、C重合),且∠1=∠C=40°,若BD=CE,则∠BAD= 度.
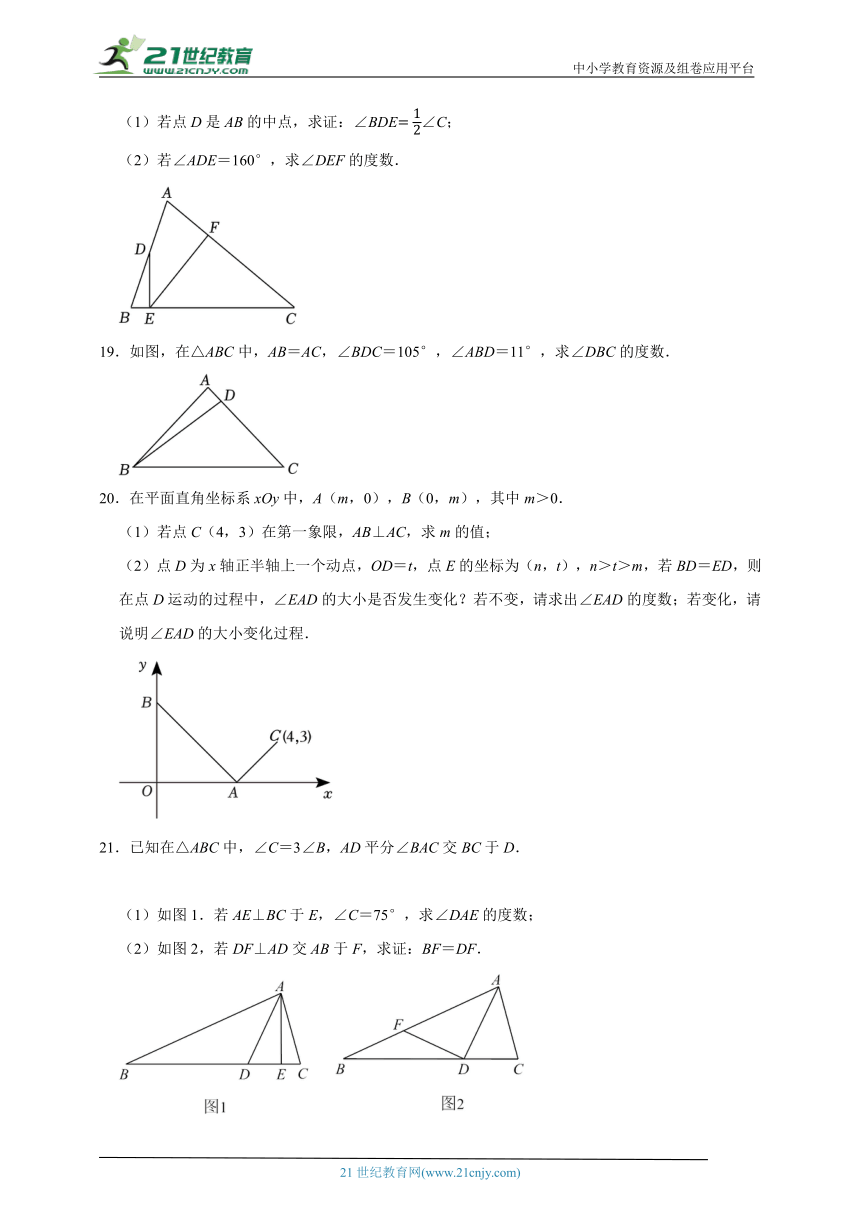
14.检测房梁是否水平,可以采用下面的方法:
在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边帖在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是: .
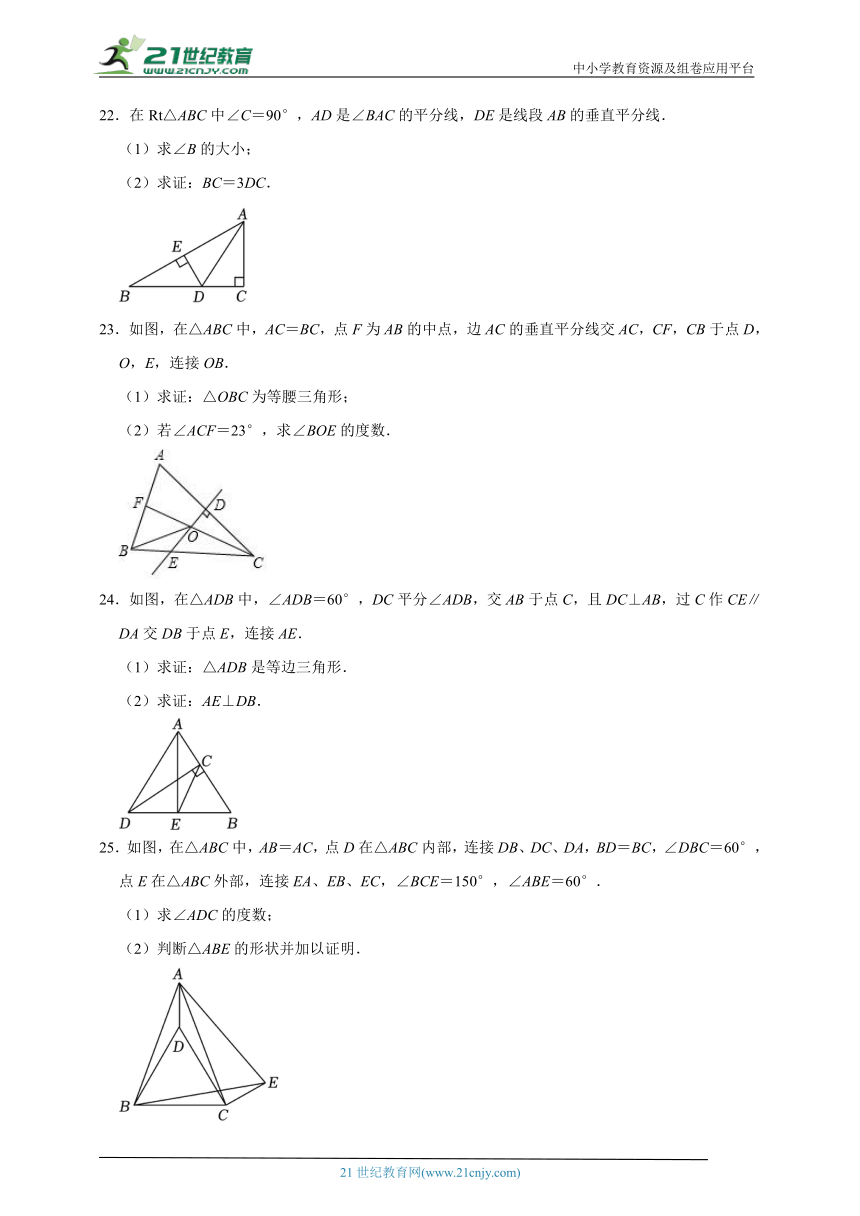
15.如图,设AB是已知线段,经过点B作 BD⊥AB,使,连接DA,在DA上截取DE=DB;在AB上截取AC=AE.已知线段AB的长为2,则线段BC的长为 .
16.“三等分角”是古希腊三大几何问题之一.如图这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=72°,则∠AOB= °.
三.解答题(共9小题)
17.有一块四边形草地ABCD(如图),测得AB=AD=5,CD=13,BC=12,∠A=60°.
(1)求∠ABC的度数;
(2)求四边形草地ABCD的面积.
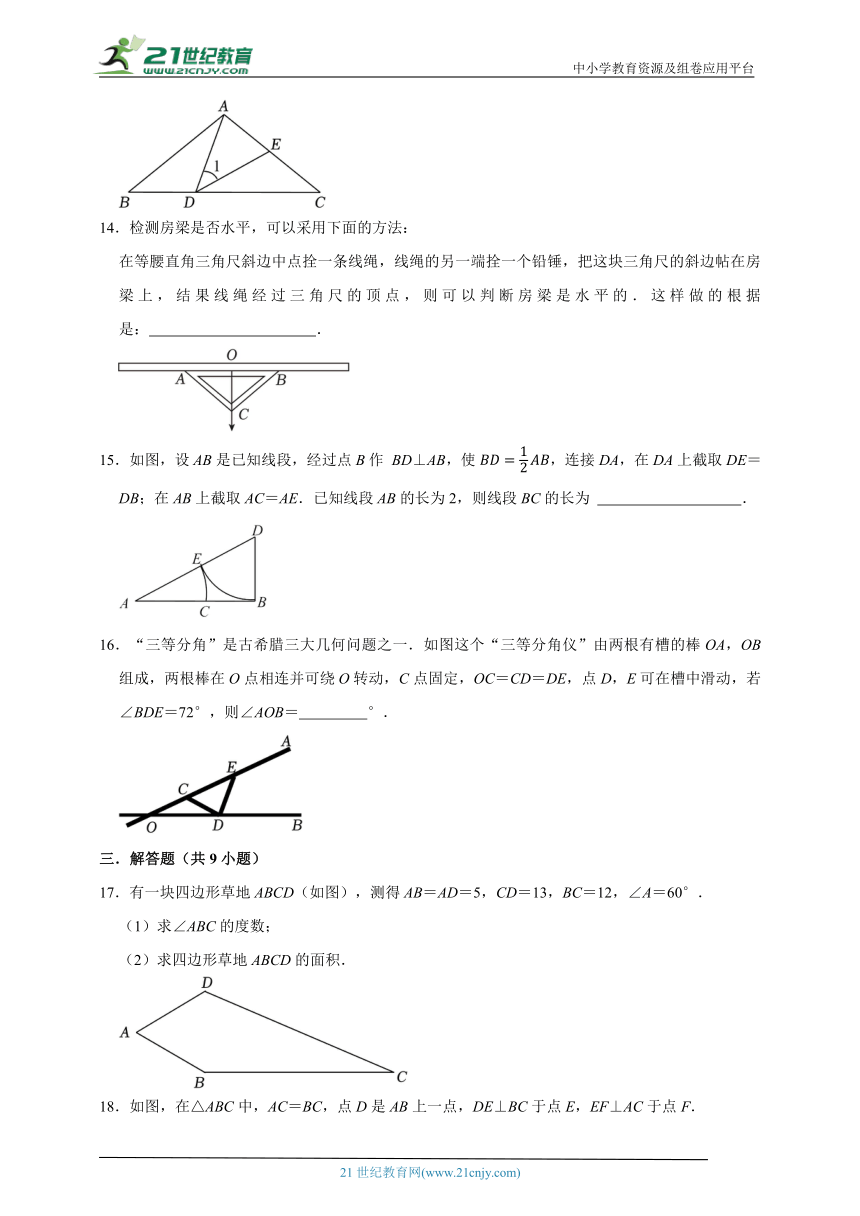
18.如图,在△ABC中,AC=BC,点D是AB上一点,DE⊥BC于点E,EF⊥AC于点F.
(1)若点D是AB的中点,求证:∠BDE∠C;
(2)若∠ADE=160°,求∠DEF的度数.
19.如图,在△ABC中,AB=AC,∠BDC=105°,∠ABD=11°,求∠DBC的度数.
20.在平面直角坐标系xOy中,A(m,0),B(0,m),其中m>0.
(1)若点C(4,3)在第一象限,AB⊥AC,求m的值;
(2)点D为x轴正半轴上一个动点,OD=t,点E的坐标为(n,t),n>t>m,若BD=ED,则在点D运动的过程中,∠EAD的大小是否发生变化?若不变,请求出∠EAD的度数;若变化,请说明∠EAD的大小变化过程.
21.已知在△ABC中,∠C=3∠B,AD平分∠BAC交BC于D.
(1)如图1.若AE⊥BC于E,∠C=75°,求∠DAE的度数;
(2)如图2,若DF⊥AD交AB于F,求证:BF=DF.
22.在Rt△ABC中∠C=90°,AD是∠BAC的平分线,DE是线段AB的垂直平分线.
(1)求∠B的大小;
(2)求证:BC=3DC.
23.如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
24.如图,在△ADB中,∠ADB=60°,DC平分∠ADB,交AB于点C,且DC⊥AB,过C作CE∥DA交DB于点E,连接AE.
(1)求证:△ADB是等边三角形.
(2)求证:AE⊥DB.
25.如图,在△ABC中,AB=AC,点D在△ABC内部,连接DB、DC、DA,BD=BC,∠DBC=60°,点E在△ABC外部,连接EA、EB、EC,∠BCE=150°,∠ABE=60°.
(1)求∠ADC的度数;
(2)判断△ABE的形状并加以证明.
1.1 等腰三角形
参考答案与试题解析
一.选择题(共10小题)
1.【答案】C
【分析】先根据AD=CD,∠A=25°求出∠ACD=25°,进而根据外角的性质求出∠BDC=50°,再根据CD=BC求出∠BDC=∠DBC=50°,根据三角形内角和求出∠BCD即可.
【解答】解:∵AD=CD,∠A=25°,
∴∠A=∠ACD=25°,
∴∠BDC=50°,
∵CD=BC,
∴∠BDC=∠DBC=50°,
∴∠BCD=180°﹣∠BDC﹣∠DBC=80°.
故选:C.
【点评】本题考查了等腰三角形的性质,解题的关键是熟练掌握等腰三角形的两个底角相等并灵活运用.
2.【答案】C
【分析】分别从①若5是底边长,10是腰长与②若10是底边长,5是腰长去分析,即可求得答案,注意检验是否能组成三角形.
【解答】解:①若5是底边长,10是腰长,
则5,10,10能组成三角形,
则它的周长是:5+10+10=25;
②若10是底边长,5是腰长,
∵5+5=10,
∴5,5,10不能组成三角形,舍去;
∴它的周长是25.
故选:C.
【点评】此题考查了等腰三角形的性质与三角形的三边关系.此题难度不大,注意分类讨论思想的应用.
3.【答案】C
【分析】根据等边三角形的性质,CE=CD的条件,可得的△BEF是含30°角的直角三角形,由此可求出BE,DE的长,根据DF=DE+EF即可求解.
【解答】解:∵△ABC是等边三角形,点E是AC的中点,
∴∠ABC=∠ACB=∠BAC=60°,DE⊥AC,DE平分∠ABC,
∴,
∵CE=CD,
∴∠CED=∠CDE,
∵∠ACB=60°,且是△CDE的外角,
∴∠CED+∠CDE=∠ACB=60°,
∴∠CED=∠CDE=30°,
∴∠AEF=∠CED=30°,
在△AEF中,∠A=60°,且∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°﹣∠A﹣∠AEF=180°﹣60°﹣30°=90°,即EF⊥AB,
∴△BEF中,∠BFE=90°,
在Rt△BEF中,∠ABE=30°,EF=2,
∴BE=2EF=2×2=4,
在△BDE中,∠EBD=∠D=30°,
∴DE=BE=4,
∴DF=DE+EF=4+2=6,
故选:C.
【点评】本题主要考查等边三角形的性质,等腰三角形的判定和性质,含30°角的直角三角形的性质的综合,掌握以上知识,图形结合分析是解题的关键.
4.【答案】C
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为2和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)若2为腰长,5为底边长,
由于2+2<5,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为5+5+2=12.
故选:C.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
5.【答案】C
【分析】根据等腰三角形的定义分边长为5的为底和为腰进行分类求解.
【解答】解:由题意可分:当边长为5的为该等腰三角形的底边时,则腰长为6,符合三角形三边关系;
当边长为5的为该等腰三角形的腰长时,则该等腰三角形的三边长为5、5、6,符合三角形三边关系;
综上所述:第三边的长为5或6;
故选:C.
【点评】本题主要考查等腰三角形的定义及三角形的三边关系,熟练掌握三角形的三边关系及等腰三角形的定义是解题的关键.
6.【答案】A
【分析】由平行线的性质、角平分线的性质推知∠E=∠ABE,则AB=AE.同理可得,AD=AC,所以线段DE的长度转化为线段AB、AC的和即可得到答案.
【解答】解:∵DE∥BC,
∴∠E=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ABE,
∴AB=AE.
同理可得:AD=AC,
∴DE=AD+AE=AB+AC=14.
故选:A.
【点评】本题综合考查了行线的性质以及等腰三角形的判定与性质,熟练掌握平行线的性质是解题的关键.
7.【答案】B
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解答】解:用反证法证明:“三角形中不能两个直角”时,
第一步先假设三角形中有两个内角是直角,
故选:B.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.
8.【答案】C
【分析】分三种情况:当MP=MN时,当NP=NM时,当PM=PN时,即可解答.
【解答】解:如图:
分三种情况:
当MP=MN时,以点M为圆心,以MN长为半径作圆,则点P1,P2即为所求;
当NP=NM时,以点N为圆心,以NM长为半径作圆,则点P3即为所求;
当PM=PN时,作线段MN的垂直平分线,则点P4,P5即为所求;
综上所述:使得△MNP为等腰三角形,则点P的个数为5个,
故选:C.
【点评】本题考查了等腰三角形的判定,分三种情况讨论是解题的关键.
9.【答案】D
【分析】分三种情况讨论,先根据题意分别画出图形,当AB=AC时,根据已知条件得出AD=BD=CD,从而得出底角的度数;当AB=BC时,先求出∠ABD的度数,再根据AB=BC求出底角的度数,当AB=BC时,求出底角.
【解答】解:①当AB=AC时,如图,
则∠B=∠C;
∵AD为BC边上的高,
∴BD=CD,
∵,
∴AD=BD=CD,
∴∠DAB=∠B,∠C=∠DAC,
∴∠DAB=∠B=∠C=∠DAC,
而这四个角和为180°,
∴底角为∠B=∠C=45°;
②当AB=BC时,如图,
∵,
∴,
∴∠ABD=30°,
∴∠BAC=∠BCA=75°,
∴底角为75°;
③当AB=BC时,如图,
∵,
∴,
∴∠ABD=30°,
∴∠BAC=∠BCA=15°,
∴底角为15°;
故选:D.
【点评】此题考查了含30度角的直角三角形和等腰三角形的性质,关键是根据题意画出图形,注意不要漏解.
10.【答案】B
【分析】先利用等角对等边可得AB=AC,然后利用等腰三角形的三线合一性质,即可解答.
【解答】解:∵∠B=∠C,
∴AB=AC,
∵AD⊥BC,
∴BD=CD,∠BAD=∠CAD,
故A、C、D正确;
∵AD与BC不一定相等,
∴B不正确;
故选:B.
【点评】本题考查了等腰三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
二.填空题(共6小题)
11.【答案】见试题解答内容
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,据此进行判断即可.
【解答】解:用反证法证明,“在△ABC中,∠A、∠B对边是a、b,若∠A>∠B,则a>b.”
第一步应假设a≤b,
故答案为:a≤b.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
12.【答案】2,20.
【分析】根据相遇问题的数量关系求得第一次两点相遇的时间为2秒和以后每相遇一次的时间6秒,即可求解.
【解答】解:∵等边△ABC 的边长为4cm,
由题意知P、Q两点第一次在等边△ABC 顶点处相遇的时间t1=2秒,
以后每隔6秒,P、Q就会相遇一次,
∴第四次在等边△ABC顶点处相遇的时间t4=3×6+2=20(秒),
故答案为:2,20.
【点评】本题主要考查了等边三角形的性质,相遇问题的应用,关键是得出P、Q第一次在等边△ABC 顶点处相遇的时间和以后每隔6秒,P、Q就会相遇一次.
13.【答案】30.
【分析】先求出∠BAC=100°,再证明△EDC≌△DAB,得到∠DAE=∠DEA,进而可求出∠BAD的度数.
【解答】解:∵AB=AC,
∴∠C=∠B.
∵∠1=∠C=40°,
∴∠1=∠C=∠B=40°,
∴∠BAC=180°﹣40°﹣40°=100°,
∵∠ADC=∠1+∠EDC=∠B+∠BAD,
∴∠EDC=∠BAD,
又∵∠C=∠B,EC=BD,
∴△EDC≌△DAB(AAS),
∴ED=AD,
∴,
∴∠BAD=∠BAC﹣∠DAE=100°﹣70°=30°.
故答案为:30.
【点评】本题考查了等腰三角形的性质,全等三角形的判定与性质,证明△EDC≌△DAB是解答本题的关键.
14.【答案】等腰三角形的底边上的中线、底边上的高重合.
【分析】根据△ABC是个等腰三角形可得AC=BC,再根据点O是AB的中点,即可得出OC⊥AB,然后即可得出结论.
【解答】解:∵△ABC是个等腰三角形,
∴AC=BC,
∵点O是AB的中点,
∴AO=BO,
∴OC⊥AB.
故答案为:等腰三角形的底边上的中线、底边上的高重合.
【点评】本题主要考查了学生对等腰三角形的性质的理解和掌握,此题与实际生活联系密切,体现了从数学走向生活的指导思想,从而达到学以致用的目的.
15.【答案】3.
【分析】根据勾股定理求出AD,求出AC,再求出BC即可.
【解答】解:∵BDAB=1,DE=DB,
∴DE=DB=1,AB=2BD=2,
由勾股定理得:AD,
∴AC=AE=AD﹣DE1,
∴BC=AB﹣AC=2﹣(1)=3,
故答案为:3.
【点评】本题考查的是勾股定理、实数与数轴,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
16.【答案】24.
【分析】根据等边对等角的性质,得到∠COD=∠CDO,∠DCE=∠DEC,再根据三角形外角的定义,得出∠DEC=2∠COD,进而求得∠COD=24°,即可得到∠AOB的度数.
【解答】解:∵OC=CD=DE,
∴∠COD=∠CDO,∠DCE=∠DEC,
∵∠DCE=∠COD+∠CDO,
∴∠DEC=2∠COD,
∴∠BDE=∠DEC+∠COD=3∠COD,∠BDE=72°,
∴∠COD=24°,
即∠AOB=24°,
故答案为:24.
【点评】本题考查了等腰三角形的性质,三角形外角的性质,熟练掌握等腰三角形等边对等角的性质是解题关键.
三.解答题(共9小题)
17.【答案】(1)150°;
(2)四边形草地ABCD的面积为30.
【分析】(1)连接BD,由等边三角形的判定证得△ABD是等边三角形,得到∠ABD=60°,再由勾股定理的逆定理证得∠CBD=90°,即可求得∠ABC;
(2)过D作DE⊥AB于E,由等腰三角形的性质求得BE,再由勾股定理求得DE,由三角形的面积公式可求得S△ABD和S△BCD,即可求得结论.
【解答】解:(1)连接BD,
∵AB=AD=5,∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=5,∠ABD=60°,
在△BCD中,BD=5,CD=13,BC=12,
∵BD2+BC2=52+122=132=CD2,
∴∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=150°;
(2)过D作DE⊥AB于E,
∵AD=BD,
∴AE=BEAB,
∴DE,
∴四边形草地ABCD的面积=S△ABD+S△BCDAB DEBC BD512×5=30,
答:四边形草地ABCD的面积为30.
【点评】本题考查了的等边三角形的性质与判定,勾股定理与勾股定理的逆定理的应用,掌握勾股定理是解题的关键.
18.【答案】(1)答案见解析;
(2)40°.
【分析】(1)连接CD,根据AC=BC,点D是AB的中点,证得CD⊥AB,,进而证得∠BCD+∠B=90°,根据DE⊥BC证得∠B+∠BDE=90°,从而证得∠BCD=∠BDE得出结论;
(2)先求出∠B的度数,再根据AC=BC求出∠A,再根据垂直的定义求出∠AFE=90°,再利用四边形的内角和为360°解答.
【解答】(1)证明:连接CD,
∵AC=BC,点D是AB的中点,
∴CD⊥AB,,
∴∠BCD+∠B=90°,
∵DE⊥BC,
∴∠B+∠BDE=90°
∴∠BCD=∠BDE.
∴;
(2)解:∵∠ADE=160°
∴∠BDE=20°,
∵DE⊥BC,EF⊥AC,
∴∠DEB=∠AFE=90°,
在Rt△BDE中,∠DEB=90°,
∴B=90°﹣∠BDE=90°﹣20°=70°,
∵AC=BC,
∴∠B=∠A=70°,
∴∠DEF=360°﹣∠A﹣∠ADE﹣∠AFE=360°﹣70°﹣160°﹣90°=40°.
【点评】本题考查了等腰三角形的性质,解题的关键是熟练掌握等腰三角形的性质并灵活运用.
19.【答案】32°.
【分析】根据三角形外角的性质求出∠A的度数,再根据等边对等角求出∠ABC的度数,即可求出∠DBC的度数.
【解答】解:∵∠BDC是△ABD的一个外角,
∴∠BDC=∠A+∠ABD,
∵∠BDC=105°,∠ABD=11°,
∴105°=∠A+11°,
∴∠A=94°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC,
∴∠DBC=∠ABC﹣∠ABD=43°﹣11°=32°.
【点评】本题考查了等腰三角形的性质,三角形外角的性质,熟知等边对等角是解题的关键.
20.【答案】(1)1;
(2)在点D运动的过程中,∠EAD的大小不发生变化,始终是45°.
【分析】(1)过点C作CH⊥x轴于H,依题意得△OAB为等腰直角三角形,则∠OAB=45°,进而得△ACH为等腰直角三角形,则AH=CH,然后根据点A(m,0),B(0,m),C(4,3),得OH=4,CH=3,AH=4﹣m,由此得4﹣m=3,由此解出m即可;
(2)依题意得点D(t,0),且点D在点A的右侧,点E在第一象限,过点E作EM⊥x轴于M,则OA=OM=m,OD=t,AD=t﹣m,证Rt△ODB和△MED全等得OB=MD=m,进而得AM=AD+MD=EM=t,从而得△AME为等腰直角三角形,则∠EAD=45°,据此可得出结论.
【解答】解:(1)过点C作CH⊥x轴于H,如图1所示:
∵A(m,0),B(0,m),其中m>0.
∴OA=OM=m,
∴△OAB为等腰直角三角形,
∴∠OAB=45°,
∵AB⊥AC,
∴∠CAH=45°,
∴△ACH为等腰直角三角形,
∴AH=CH,
∵点C(4,3),
∴OH=4,CH=3,
∴AH=4﹣m,
∴4﹣m=3,
解得:m=1;
(2)∵点D为x轴正半轴上一个动点,OD=t,点E(n,t),n>t>m,
∴点D(t,0),且点D在点A的右侧,点E在第一象限,
过点E作EM⊥x轴于M,如图2所示:
∵OA=OM=m,OD=t,
∴AD=OD﹣OA=t﹣m,
∵点E(n,t),
∴EM=t,
∴OD=EM,
在Rt△ODB和△MED中,
,
∴Rt△ODB≌△MED(HL),
∴OB=MD=m,
∴AM=AD+MD=t﹣m+m=t,
∴AM=EM=t,
∴△AME为等腰直角三角形,
∴∠EAD=45°.
∴在点D运动的过程中,∠EAD的大小不发生变化,始终是45°.
【点评】此题主要考查了坐标与图形,等腰三角形的判定和性质,熟练掌握点的坐标,理解等腰三角形的判定和性质是解决问题的关键.
21.【答案】(1)25°;
(2)证明见解析.
【分析】(1)根据角平分线的定义和垂直的定义解答即可;
(2)根据角平分线的定义和等腰三角形的判定解答即可.
【解答】(1)解:∵∠C=3∠B,∠C=75°,
∴∠B=25°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AD平分∠BAC,
∴∠BAD∠BAC=40°,
∴∠ADE=∠BAD+∠B=65°,
∵AE⊥BC,
∴∠AED=90°,
∴∠DAE=90°﹣∠ADE=90°﹣65°=25°,
(2)证明:设∠B=α,则∠C=3α,∠BAC=180°﹣∠B﹣∠C=180°﹣4α,
∵AD平分∠BAC,
∴∠BAD∠BAC,
∵DF⊥AD,
∴∠ADF=90°,
∴∠AFD=90°﹣∠BAD=2α,
∵∠AFD=∠B+∠BDF,
∴∠BDF=α=∠B,
∴BF=DF.
【点评】此题考查等腰三角形的判定,关键是根据角平分线的定义和垂直的定义解答.
22.【答案】(1)∠B的度数为30°;
(2)证明过程见解答.
【分析】(1)根据直角三角形的两个锐角互余可得∠B+∠BAC=90°,从而可得∠B+∠BAD+∠DAC=90°,然后根据角平分线的定义可得∠BAD=∠DAC,
再根据线段垂直平分线的性质可得DA=DB,从而可得∠B=∠BAD=∠DAC=30°,即可解答;
(2)在Rt△BDE中,利用含30度角的直角三角形的性质可得BD=2DE,然后利用角平分线的性质可得DE=DC,从而进行计算即可解答.
【解答】(1)解:∵∠C=90°,
∴∠B+∠BAC=90°,
∴∠B+∠BAD+∠DAC=90°,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵DE是AB垂直平分线,
∴DA=DB,
∴∠B=∠BAD,
∴∠B=∠BAD=∠DAC=30°,
∴∠B的度数为30°;
(2)证明:在Rt△BDE中,∠B=30°,
∴BD=2DE,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC,
∴BD=2CD,
∴BC=3DC.
【点评】本题考查了含30度角的直角三角形,线段垂直平分线的性质,熟练掌握含30度角的直角三角形,以及线段垂直平分线的性质是解题的关键.
23.【答案】见试题解答内容
【分析】(1)连接OA,如图,利用等腰三角形的性质得到CF⊥AB,则CF垂直平分AB,根据线段垂直平分线的性质得到OA=OB,OA=OC,所以OB=OC,从而得到结论;
(2)利用等腰三角形的性质得到CF平分∠ACB,则∠BCF=∠ACF=23°,再利用OB=OC得到∠OBC=∠OCB=23°,接着根据互余计算出∠DEC=44°,然后根据三角形外角性质计算∠BOE的度数.
【解答】(1)证明:连接OA,如图,
∵AC=BC,点F为AB的中点,
∴CF⊥AB,
∴CF垂直平分AB,
∴OA=OB,
∵DE垂直平分AC,
∴OA=OC,
∴OB=OC,
∴△OBC为等腰三角形;
(2)解:∵CA=CB,CF⊥AB,
∴CF平分∠ACB,
∴∠BCF=∠ACF=23°,
∵OB=OC,
∴∠OBC=∠OCB=23°,
∵∠EDC=90°
∴∠DEC=90°﹣∠DCE=90°﹣23°﹣23°=44°,
∵∠OEC=∠OBE+∠BOE,
∴∠BOE=44°﹣23°=21°.
【点评】本题考查了等腰三角形的判定与性质:等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.也考查了线段垂直平分线的性质.
24.【答案】见解析.
【分析】(1)直接根据等边三角形的判定定理可得结论;
(2)由平行线的性质可得∠BEC=∠ADB=60,根据等边三角形的判定与性质可得CE=BE=CB,再由直角三角形的性质可得AE是边BD的中线,最后再由等边三角形的性质可得答案.
【解答】证明:(1)∵DC平分∠ADB,
∴∠ADC=∠BDC,
∵∠ADB=60°,
∴∠ADC=∠BCD=30°,
∵DC⊥AB,
∴∠DCB=∠DCA=90°,
∴∠B=∠A=90°﹣30°=60°,
∴∠AOB=∠B=∠DAB=60°,
∴△ADB是等边三角形;
(2)∵CE∥DA,
∴∠BEC=∠ADB=60,
∴∠CEB=∠CBE=∠ECB=60°,
∴△CEB是等边三角形,
∴CE=BE=CB,
∵∠BDC=30°,∠DCB=90°,
∴BCBD,
∴CEBD,
∴E是BD的中点,
∴AE是边BD的中线,
∵△ADB是等边三角形,
∴AE⊥BD.
【点评】此题考查的是等边三角形的判定与性质、平行线的性质、直角三角形的性质等知识,掌握其性质定理是解决此题的关键.
25.【答案】(1)见解答;
(2)见解答.
【分析】(1)首先证明△DBC是等边三角形,推出∠BDC=60°,再证明△ADB≌△ADC,推出∠ADB=∠ADC即可解决问题.
(2)只要证明△ABD≌△EBC得到AB=BE即可证明△ABE是等边三角形.
【解答】解:(1)∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴∠BDC=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS),
∴∠ADB=∠ADC,
∴.
(2)△ABE是等边三角形,证明如下:
∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(ASA),
∴AB=BE,
∵∠ABE=60°,
∴△ABE是等边三角形.
【点评】本题主要考查了等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,含30度角的直角三角形的性质,解题的关键是熟练掌握全等三角形的判定和性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1 等腰三角形
一.选择题(共10小题)
1.如图,在△ABC中,D是边AB上一点,AD=CD=BC,∠A=25°,则∠BCD的度数为( )
A.50° B.65° C.80° D.105°
2.等腰三角形的两边分别为5和10,则它的周长是( )
A.20 B.15 C.25 D.20或25
3.如图,△ABC是等边三角形,点D在BC的延长线上,点E是AC的中点,连接DE并延长交AB于点F,且CE=CD,若EF=2,则DF的长为( )
A.3 B.4 C.6 D.8
4.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
5.已知等腰三角形的两边长分别是5和6,则第三边的长是( )
A.5 B.6 C.5或6 D.10
6.如图,在△ABC中,∠BAC=90°,AC=6,AB=8,过点A的直线DE∥BC,∠ABC与∠ACB的平分线分别交DE于E,D,则DE的长为( )
A.14 B.16 C.18 D.20
7.牛顿曾说过:反证法是数学家最精良的武器之一,我们用反证法证明命题“三角形中不能两个直角”,应先假设( )
A.三角形中有一个内角是直角
B.三角形中有两个内角是直角
C.三角形中有三个内角是直角
D.三角形中不能有内角是直角
8.如图,M,N为4×4方格纸中格点上的两点,若以MN为边,在方格中取一点P(P在格点上),使得△MNP为等腰三角形,则点P的个数为( )
A.3个 B.4个 C.5个 D.6个
9.已知等腰△ABC,AD为BC边上的高,且,则等腰△ABC的底角的度数为( )
A.45° B.75°或60°
C.45°或75° D.以上都不对
10.如图,△ABC中,∠B=∠C,AD为BC边上的高,下列结论中不正确的是( )
A.AB=AC B.AD=BC C.BD=CD D.∠BAD=∠CAD
二.填空题(共6小题)
11.用反证法证明,“在△ABC中,∠A、∠B对边是a、b,若∠A>∠B,则a>b.”第一步应假设 .
12.如图,等边△ABC 的边长为4cm,P、Q两点分别从A、B两点同时出发,点P以8cm/s的速度按顺时针方向在等边△ABC的边上运动,点Q以2cm/s的速度按逆时针方向在等边△ABC的边上运动,则P、Q两点第一次在等边△ABC 顶点处相遇的时间t1= 秒,第四次在等边△ABC顶点处相遇的时间t4= 秒.
13.如图,在△ABC中,AB=AC,点D、E分别在边BC、AC上(均不与点A、B、C重合),且∠1=∠C=40°,若BD=CE,则∠BAD= 度.
14.检测房梁是否水平,可以采用下面的方法:
在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边帖在房梁上,结果线绳经过三角尺的顶点,则可以判断房梁是水平的.这样做的根据是: .
15.如图,设AB是已知线段,经过点B作 BD⊥AB,使,连接DA,在DA上截取DE=DB;在AB上截取AC=AE.已知线段AB的长为2,则线段BC的长为 .
16.“三等分角”是古希腊三大几何问题之一.如图这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=72°,则∠AOB= °.
三.解答题(共9小题)
17.有一块四边形草地ABCD(如图),测得AB=AD=5,CD=13,BC=12,∠A=60°.
(1)求∠ABC的度数;
(2)求四边形草地ABCD的面积.
18.如图,在△ABC中,AC=BC,点D是AB上一点,DE⊥BC于点E,EF⊥AC于点F.
(1)若点D是AB的中点,求证:∠BDE∠C;
(2)若∠ADE=160°,求∠DEF的度数.
19.如图,在△ABC中,AB=AC,∠BDC=105°,∠ABD=11°,求∠DBC的度数.
20.在平面直角坐标系xOy中,A(m,0),B(0,m),其中m>0.
(1)若点C(4,3)在第一象限,AB⊥AC,求m的值;
(2)点D为x轴正半轴上一个动点,OD=t,点E的坐标为(n,t),n>t>m,若BD=ED,则在点D运动的过程中,∠EAD的大小是否发生变化?若不变,请求出∠EAD的度数;若变化,请说明∠EAD的大小变化过程.
21.已知在△ABC中,∠C=3∠B,AD平分∠BAC交BC于D.
(1)如图1.若AE⊥BC于E,∠C=75°,求∠DAE的度数;
(2)如图2,若DF⊥AD交AB于F,求证:BF=DF.
22.在Rt△ABC中∠C=90°,AD是∠BAC的平分线,DE是线段AB的垂直平分线.
(1)求∠B的大小;
(2)求证:BC=3DC.
23.如图,在△ABC中,AC=BC,点F为AB的中点,边AC的垂直平分线交AC,CF,CB于点D,O,E,连接OB.
(1)求证:△OBC为等腰三角形;
(2)若∠ACF=23°,求∠BOE的度数.
24.如图,在△ADB中,∠ADB=60°,DC平分∠ADB,交AB于点C,且DC⊥AB,过C作CE∥DA交DB于点E,连接AE.
(1)求证:△ADB是等边三角形.
(2)求证:AE⊥DB.
25.如图,在△ABC中,AB=AC,点D在△ABC内部,连接DB、DC、DA,BD=BC,∠DBC=60°,点E在△ABC外部,连接EA、EB、EC,∠BCE=150°,∠ABE=60°.
(1)求∠ADC的度数;
(2)判断△ABE的形状并加以证明.
1.1 等腰三角形
参考答案与试题解析
一.选择题(共10小题)
1.【答案】C
【分析】先根据AD=CD,∠A=25°求出∠ACD=25°,进而根据外角的性质求出∠BDC=50°,再根据CD=BC求出∠BDC=∠DBC=50°,根据三角形内角和求出∠BCD即可.
【解答】解:∵AD=CD,∠A=25°,
∴∠A=∠ACD=25°,
∴∠BDC=50°,
∵CD=BC,
∴∠BDC=∠DBC=50°,
∴∠BCD=180°﹣∠BDC﹣∠DBC=80°.
故选:C.
【点评】本题考查了等腰三角形的性质,解题的关键是熟练掌握等腰三角形的两个底角相等并灵活运用.
2.【答案】C
【分析】分别从①若5是底边长,10是腰长与②若10是底边长,5是腰长去分析,即可求得答案,注意检验是否能组成三角形.
【解答】解:①若5是底边长,10是腰长,
则5,10,10能组成三角形,
则它的周长是:5+10+10=25;
②若10是底边长,5是腰长,
∵5+5=10,
∴5,5,10不能组成三角形,舍去;
∴它的周长是25.
故选:C.
【点评】此题考查了等腰三角形的性质与三角形的三边关系.此题难度不大,注意分类讨论思想的应用.
3.【答案】C
【分析】根据等边三角形的性质,CE=CD的条件,可得的△BEF是含30°角的直角三角形,由此可求出BE,DE的长,根据DF=DE+EF即可求解.
【解答】解:∵△ABC是等边三角形,点E是AC的中点,
∴∠ABC=∠ACB=∠BAC=60°,DE⊥AC,DE平分∠ABC,
∴,
∵CE=CD,
∴∠CED=∠CDE,
∵∠ACB=60°,且是△CDE的外角,
∴∠CED+∠CDE=∠ACB=60°,
∴∠CED=∠CDE=30°,
∴∠AEF=∠CED=30°,
在△AEF中,∠A=60°,且∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°﹣∠A﹣∠AEF=180°﹣60°﹣30°=90°,即EF⊥AB,
∴△BEF中,∠BFE=90°,
在Rt△BEF中,∠ABE=30°,EF=2,
∴BE=2EF=2×2=4,
在△BDE中,∠EBD=∠D=30°,
∴DE=BE=4,
∴DF=DE+EF=4+2=6,
故选:C.
【点评】本题主要考查等边三角形的性质,等腰三角形的判定和性质,含30°角的直角三角形的性质的综合,掌握以上知识,图形结合分析是解题的关键.
4.【答案】C
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为2和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)若2为腰长,5为底边长,
由于2+2<5,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为5+5+2=12.
故选:C.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.
5.【答案】C
【分析】根据等腰三角形的定义分边长为5的为底和为腰进行分类求解.
【解答】解:由题意可分:当边长为5的为该等腰三角形的底边时,则腰长为6,符合三角形三边关系;
当边长为5的为该等腰三角形的腰长时,则该等腰三角形的三边长为5、5、6,符合三角形三边关系;
综上所述:第三边的长为5或6;
故选:C.
【点评】本题主要考查等腰三角形的定义及三角形的三边关系,熟练掌握三角形的三边关系及等腰三角形的定义是解题的关键.
6.【答案】A
【分析】由平行线的性质、角平分线的性质推知∠E=∠ABE,则AB=AE.同理可得,AD=AC,所以线段DE的长度转化为线段AB、AC的和即可得到答案.
【解答】解:∵DE∥BC,
∴∠E=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ABE,
∴AB=AE.
同理可得:AD=AC,
∴DE=AD+AE=AB+AC=14.
故选:A.
【点评】本题综合考查了行线的性质以及等腰三角形的判定与性质,熟练掌握平行线的性质是解题的关键.
7.【答案】B
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解答】解:用反证法证明:“三角形中不能两个直角”时,
第一步先假设三角形中有两个内角是直角,
故选:B.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.
8.【答案】C
【分析】分三种情况:当MP=MN时,当NP=NM时,当PM=PN时,即可解答.
【解答】解:如图:
分三种情况:
当MP=MN时,以点M为圆心,以MN长为半径作圆,则点P1,P2即为所求;
当NP=NM时,以点N为圆心,以NM长为半径作圆,则点P3即为所求;
当PM=PN时,作线段MN的垂直平分线,则点P4,P5即为所求;
综上所述:使得△MNP为等腰三角形,则点P的个数为5个,
故选:C.
【点评】本题考查了等腰三角形的判定,分三种情况讨论是解题的关键.
9.【答案】D
【分析】分三种情况讨论,先根据题意分别画出图形,当AB=AC时,根据已知条件得出AD=BD=CD,从而得出底角的度数;当AB=BC时,先求出∠ABD的度数,再根据AB=BC求出底角的度数,当AB=BC时,求出底角.
【解答】解:①当AB=AC时,如图,
则∠B=∠C;
∵AD为BC边上的高,
∴BD=CD,
∵,
∴AD=BD=CD,
∴∠DAB=∠B,∠C=∠DAC,
∴∠DAB=∠B=∠C=∠DAC,
而这四个角和为180°,
∴底角为∠B=∠C=45°;
②当AB=BC时,如图,
∵,
∴,
∴∠ABD=30°,
∴∠BAC=∠BCA=75°,
∴底角为75°;
③当AB=BC时,如图,
∵,
∴,
∴∠ABD=30°,
∴∠BAC=∠BCA=15°,
∴底角为15°;
故选:D.
【点评】此题考查了含30度角的直角三角形和等腰三角形的性质,关键是根据题意画出图形,注意不要漏解.
10.【答案】B
【分析】先利用等角对等边可得AB=AC,然后利用等腰三角形的三线合一性质,即可解答.
【解答】解:∵∠B=∠C,
∴AB=AC,
∵AD⊥BC,
∴BD=CD,∠BAD=∠CAD,
故A、C、D正确;
∵AD与BC不一定相等,
∴B不正确;
故选:B.
【点评】本题考查了等腰三角形的判定与性质,熟练掌握等腰三角形的判定与性质是解题的关键.
二.填空题(共6小题)
11.【答案】见试题解答内容
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,据此进行判断即可.
【解答】解:用反证法证明,“在△ABC中,∠A、∠B对边是a、b,若∠A>∠B,则a>b.”
第一步应假设a≤b,
故答案为:a≤b.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
12.【答案】2,20.
【分析】根据相遇问题的数量关系求得第一次两点相遇的时间为2秒和以后每相遇一次的时间6秒,即可求解.
【解答】解:∵等边△ABC 的边长为4cm,
由题意知P、Q两点第一次在等边△ABC 顶点处相遇的时间t1=2秒,
以后每隔6秒,P、Q就会相遇一次,
∴第四次在等边△ABC顶点处相遇的时间t4=3×6+2=20(秒),
故答案为:2,20.
【点评】本题主要考查了等边三角形的性质,相遇问题的应用,关键是得出P、Q第一次在等边△ABC 顶点处相遇的时间和以后每隔6秒,P、Q就会相遇一次.
13.【答案】30.
【分析】先求出∠BAC=100°,再证明△EDC≌△DAB,得到∠DAE=∠DEA,进而可求出∠BAD的度数.
【解答】解:∵AB=AC,
∴∠C=∠B.
∵∠1=∠C=40°,
∴∠1=∠C=∠B=40°,
∴∠BAC=180°﹣40°﹣40°=100°,
∵∠ADC=∠1+∠EDC=∠B+∠BAD,
∴∠EDC=∠BAD,
又∵∠C=∠B,EC=BD,
∴△EDC≌△DAB(AAS),
∴ED=AD,
∴,
∴∠BAD=∠BAC﹣∠DAE=100°﹣70°=30°.
故答案为:30.
【点评】本题考查了等腰三角形的性质,全等三角形的判定与性质,证明△EDC≌△DAB是解答本题的关键.
14.【答案】等腰三角形的底边上的中线、底边上的高重合.
【分析】根据△ABC是个等腰三角形可得AC=BC,再根据点O是AB的中点,即可得出OC⊥AB,然后即可得出结论.
【解答】解:∵△ABC是个等腰三角形,
∴AC=BC,
∵点O是AB的中点,
∴AO=BO,
∴OC⊥AB.
故答案为:等腰三角形的底边上的中线、底边上的高重合.
【点评】本题主要考查了学生对等腰三角形的性质的理解和掌握,此题与实际生活联系密切,体现了从数学走向生活的指导思想,从而达到学以致用的目的.
15.【答案】3.
【分析】根据勾股定理求出AD,求出AC,再求出BC即可.
【解答】解:∵BDAB=1,DE=DB,
∴DE=DB=1,AB=2BD=2,
由勾股定理得:AD,
∴AC=AE=AD﹣DE1,
∴BC=AB﹣AC=2﹣(1)=3,
故答案为:3.
【点评】本题考查的是勾股定理、实数与数轴,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
16.【答案】24.
【分析】根据等边对等角的性质,得到∠COD=∠CDO,∠DCE=∠DEC,再根据三角形外角的定义,得出∠DEC=2∠COD,进而求得∠COD=24°,即可得到∠AOB的度数.
【解答】解:∵OC=CD=DE,
∴∠COD=∠CDO,∠DCE=∠DEC,
∵∠DCE=∠COD+∠CDO,
∴∠DEC=2∠COD,
∴∠BDE=∠DEC+∠COD=3∠COD,∠BDE=72°,
∴∠COD=24°,
即∠AOB=24°,
故答案为:24.
【点评】本题考查了等腰三角形的性质,三角形外角的性质,熟练掌握等腰三角形等边对等角的性质是解题关键.
三.解答题(共9小题)
17.【答案】(1)150°;
(2)四边形草地ABCD的面积为30.
【分析】(1)连接BD,由等边三角形的判定证得△ABD是等边三角形,得到∠ABD=60°,再由勾股定理的逆定理证得∠CBD=90°,即可求得∠ABC;
(2)过D作DE⊥AB于E,由等腰三角形的性质求得BE,再由勾股定理求得DE,由三角形的面积公式可求得S△ABD和S△BCD,即可求得结论.
【解答】解:(1)连接BD,
∵AB=AD=5,∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=5,∠ABD=60°,
在△BCD中,BD=5,CD=13,BC=12,
∵BD2+BC2=52+122=132=CD2,
∴∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=150°;
(2)过D作DE⊥AB于E,
∵AD=BD,
∴AE=BEAB,
∴DE,
∴四边形草地ABCD的面积=S△ABD+S△BCDAB DEBC BD512×5=30,
答:四边形草地ABCD的面积为30.
【点评】本题考查了的等边三角形的性质与判定,勾股定理与勾股定理的逆定理的应用,掌握勾股定理是解题的关键.
18.【答案】(1)答案见解析;
(2)40°.
【分析】(1)连接CD,根据AC=BC,点D是AB的中点,证得CD⊥AB,,进而证得∠BCD+∠B=90°,根据DE⊥BC证得∠B+∠BDE=90°,从而证得∠BCD=∠BDE得出结论;
(2)先求出∠B的度数,再根据AC=BC求出∠A,再根据垂直的定义求出∠AFE=90°,再利用四边形的内角和为360°解答.
【解答】(1)证明:连接CD,
∵AC=BC,点D是AB的中点,
∴CD⊥AB,,
∴∠BCD+∠B=90°,
∵DE⊥BC,
∴∠B+∠BDE=90°
∴∠BCD=∠BDE.
∴;
(2)解:∵∠ADE=160°
∴∠BDE=20°,
∵DE⊥BC,EF⊥AC,
∴∠DEB=∠AFE=90°,
在Rt△BDE中,∠DEB=90°,
∴B=90°﹣∠BDE=90°﹣20°=70°,
∵AC=BC,
∴∠B=∠A=70°,
∴∠DEF=360°﹣∠A﹣∠ADE﹣∠AFE=360°﹣70°﹣160°﹣90°=40°.
【点评】本题考查了等腰三角形的性质,解题的关键是熟练掌握等腰三角形的性质并灵活运用.
19.【答案】32°.
【分析】根据三角形外角的性质求出∠A的度数,再根据等边对等角求出∠ABC的度数,即可求出∠DBC的度数.
【解答】解:∵∠BDC是△ABD的一个外角,
∴∠BDC=∠A+∠ABD,
∵∠BDC=105°,∠ABD=11°,
∴105°=∠A+11°,
∴∠A=94°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC,
∴∠DBC=∠ABC﹣∠ABD=43°﹣11°=32°.
【点评】本题考查了等腰三角形的性质,三角形外角的性质,熟知等边对等角是解题的关键.
20.【答案】(1)1;
(2)在点D运动的过程中,∠EAD的大小不发生变化,始终是45°.
【分析】(1)过点C作CH⊥x轴于H,依题意得△OAB为等腰直角三角形,则∠OAB=45°,进而得△ACH为等腰直角三角形,则AH=CH,然后根据点A(m,0),B(0,m),C(4,3),得OH=4,CH=3,AH=4﹣m,由此得4﹣m=3,由此解出m即可;
(2)依题意得点D(t,0),且点D在点A的右侧,点E在第一象限,过点E作EM⊥x轴于M,则OA=OM=m,OD=t,AD=t﹣m,证Rt△ODB和△MED全等得OB=MD=m,进而得AM=AD+MD=EM=t,从而得△AME为等腰直角三角形,则∠EAD=45°,据此可得出结论.
【解答】解:(1)过点C作CH⊥x轴于H,如图1所示:
∵A(m,0),B(0,m),其中m>0.
∴OA=OM=m,
∴△OAB为等腰直角三角形,
∴∠OAB=45°,
∵AB⊥AC,
∴∠CAH=45°,
∴△ACH为等腰直角三角形,
∴AH=CH,
∵点C(4,3),
∴OH=4,CH=3,
∴AH=4﹣m,
∴4﹣m=3,
解得:m=1;
(2)∵点D为x轴正半轴上一个动点,OD=t,点E(n,t),n>t>m,
∴点D(t,0),且点D在点A的右侧,点E在第一象限,
过点E作EM⊥x轴于M,如图2所示:
∵OA=OM=m,OD=t,
∴AD=OD﹣OA=t﹣m,
∵点E(n,t),
∴EM=t,
∴OD=EM,
在Rt△ODB和△MED中,
,
∴Rt△ODB≌△MED(HL),
∴OB=MD=m,
∴AM=AD+MD=t﹣m+m=t,
∴AM=EM=t,
∴△AME为等腰直角三角形,
∴∠EAD=45°.
∴在点D运动的过程中,∠EAD的大小不发生变化,始终是45°.
【点评】此题主要考查了坐标与图形,等腰三角形的判定和性质,熟练掌握点的坐标,理解等腰三角形的判定和性质是解决问题的关键.
21.【答案】(1)25°;
(2)证明见解析.
【分析】(1)根据角平分线的定义和垂直的定义解答即可;
(2)根据角平分线的定义和等腰三角形的判定解答即可.
【解答】(1)解:∵∠C=3∠B,∠C=75°,
∴∠B=25°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
∵AD平分∠BAC,
∴∠BAD∠BAC=40°,
∴∠ADE=∠BAD+∠B=65°,
∵AE⊥BC,
∴∠AED=90°,
∴∠DAE=90°﹣∠ADE=90°﹣65°=25°,
(2)证明:设∠B=α,则∠C=3α,∠BAC=180°﹣∠B﹣∠C=180°﹣4α,
∵AD平分∠BAC,
∴∠BAD∠BAC,
∵DF⊥AD,
∴∠ADF=90°,
∴∠AFD=90°﹣∠BAD=2α,
∵∠AFD=∠B+∠BDF,
∴∠BDF=α=∠B,
∴BF=DF.
【点评】此题考查等腰三角形的判定,关键是根据角平分线的定义和垂直的定义解答.
22.【答案】(1)∠B的度数为30°;
(2)证明过程见解答.
【分析】(1)根据直角三角形的两个锐角互余可得∠B+∠BAC=90°,从而可得∠B+∠BAD+∠DAC=90°,然后根据角平分线的定义可得∠BAD=∠DAC,
再根据线段垂直平分线的性质可得DA=DB,从而可得∠B=∠BAD=∠DAC=30°,即可解答;
(2)在Rt△BDE中,利用含30度角的直角三角形的性质可得BD=2DE,然后利用角平分线的性质可得DE=DC,从而进行计算即可解答.
【解答】(1)解:∵∠C=90°,
∴∠B+∠BAC=90°,
∴∠B+∠BAD+∠DAC=90°,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵DE是AB垂直平分线,
∴DA=DB,
∴∠B=∠BAD,
∴∠B=∠BAD=∠DAC=30°,
∴∠B的度数为30°;
(2)证明:在Rt△BDE中,∠B=30°,
∴BD=2DE,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC,
∴BD=2CD,
∴BC=3DC.
【点评】本题考查了含30度角的直角三角形,线段垂直平分线的性质,熟练掌握含30度角的直角三角形,以及线段垂直平分线的性质是解题的关键.
23.【答案】见试题解答内容
【分析】(1)连接OA,如图,利用等腰三角形的性质得到CF⊥AB,则CF垂直平分AB,根据线段垂直平分线的性质得到OA=OB,OA=OC,所以OB=OC,从而得到结论;
(2)利用等腰三角形的性质得到CF平分∠ACB,则∠BCF=∠ACF=23°,再利用OB=OC得到∠OBC=∠OCB=23°,接着根据互余计算出∠DEC=44°,然后根据三角形外角性质计算∠BOE的度数.
【解答】(1)证明:连接OA,如图,
∵AC=BC,点F为AB的中点,
∴CF⊥AB,
∴CF垂直平分AB,
∴OA=OB,
∵DE垂直平分AC,
∴OA=OC,
∴OB=OC,
∴△OBC为等腰三角形;
(2)解:∵CA=CB,CF⊥AB,
∴CF平分∠ACB,
∴∠BCF=∠ACF=23°,
∵OB=OC,
∴∠OBC=∠OCB=23°,
∵∠EDC=90°
∴∠DEC=90°﹣∠DCE=90°﹣23°﹣23°=44°,
∵∠OEC=∠OBE+∠BOE,
∴∠BOE=44°﹣23°=21°.
【点评】本题考查了等腰三角形的判定与性质:等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.也考查了线段垂直平分线的性质.
24.【答案】见解析.
【分析】(1)直接根据等边三角形的判定定理可得结论;
(2)由平行线的性质可得∠BEC=∠ADB=60,根据等边三角形的判定与性质可得CE=BE=CB,再由直角三角形的性质可得AE是边BD的中线,最后再由等边三角形的性质可得答案.
【解答】证明:(1)∵DC平分∠ADB,
∴∠ADC=∠BDC,
∵∠ADB=60°,
∴∠ADC=∠BCD=30°,
∵DC⊥AB,
∴∠DCB=∠DCA=90°,
∴∠B=∠A=90°﹣30°=60°,
∴∠AOB=∠B=∠DAB=60°,
∴△ADB是等边三角形;
(2)∵CE∥DA,
∴∠BEC=∠ADB=60,
∴∠CEB=∠CBE=∠ECB=60°,
∴△CEB是等边三角形,
∴CE=BE=CB,
∵∠BDC=30°,∠DCB=90°,
∴BCBD,
∴CEBD,
∴E是BD的中点,
∴AE是边BD的中线,
∵△ADB是等边三角形,
∴AE⊥BD.
【点评】此题考查的是等边三角形的判定与性质、平行线的性质、直角三角形的性质等知识,掌握其性质定理是解决此题的关键.
25.【答案】(1)见解答;
(2)见解答.
【分析】(1)首先证明△DBC是等边三角形,推出∠BDC=60°,再证明△ADB≌△ADC,推出∠ADB=∠ADC即可解决问题.
(2)只要证明△ABD≌△EBC得到AB=BE即可证明△ABE是等边三角形.
【解答】解:(1)∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴∠BDC=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS),
∴∠ADB=∠ADC,
∴.
(2)△ABE是等边三角形,证明如下:
∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(ASA),
∴AB=BE,
∵∠ABE=60°,
∴△ABE是等边三角形.
【点评】本题主要考查了等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,含30度角的直角三角形的性质,解题的关键是熟练掌握全等三角形的判定和性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
