1.3 三角函数的计算(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学九年级下册
文档属性
| 名称 | 1.3 三角函数的计算(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 239.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:40:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.3 三角函数的计算
一.选择题(共10小题)
1.为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A.
B.
C.
D.
2.利用计算器计算cos55°,下列按键顺序正确的是( )
A.
B.
C.
D.
3.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
4.如图,在△ABC中,∠C=90°,∠B=43°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A. B.
C. D.
5.若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是( )
A.
B.
C.
D.
6.如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算cos55°,按键顺序正确的是( )
A.
B.
C.
D.
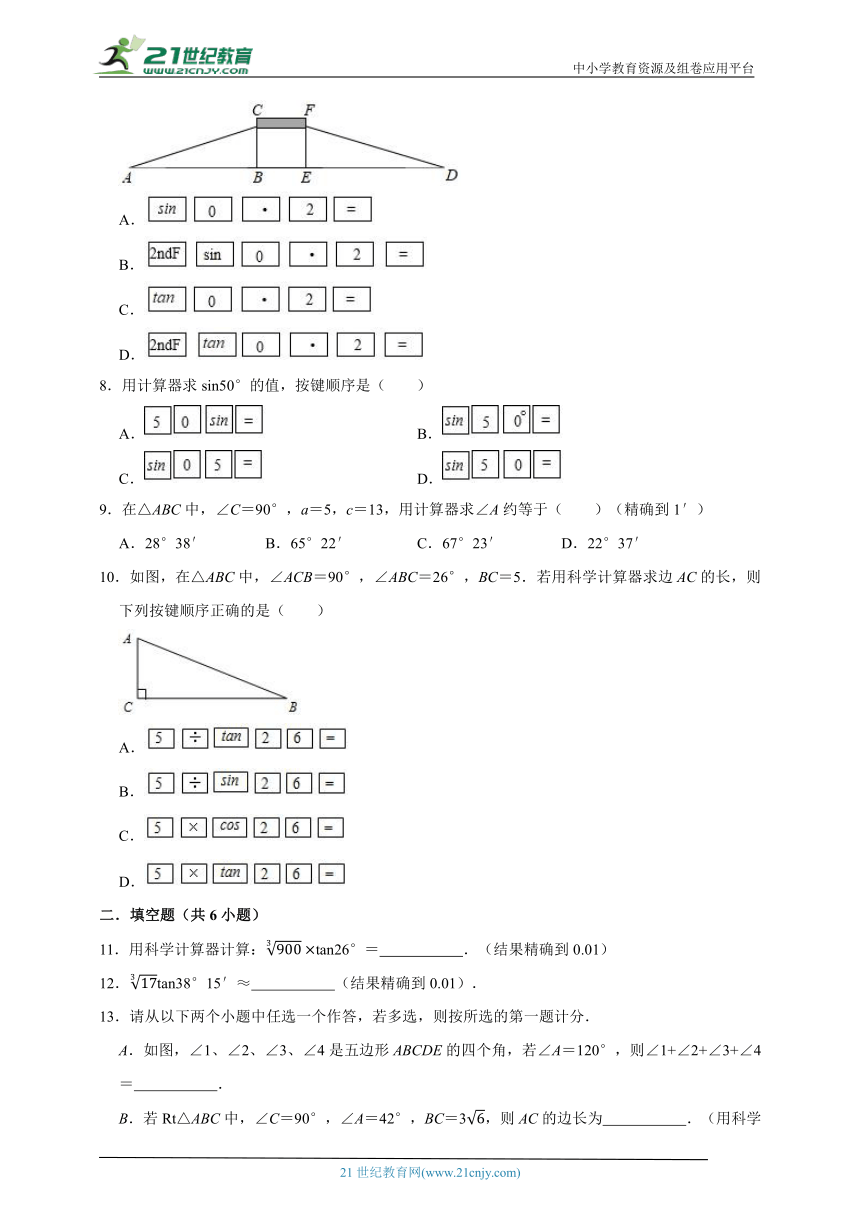
7.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
8.用计算器求sin50°的值,按键顺序是( )
A. B.
C. D.
9.在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于( )(精确到1′)
A.28°38′ B.65°22′ C.67°23′ D.22°37′
10.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
二.填空题(共6小题)
11.用科学计算器计算:tan26°= .(结果精确到0.01)
12.tan38°15′≈ (结果精确到0.01).
13.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,∠1、∠2、∠3、∠4是五边形ABCDE的四个角,若∠A=120°,则∠1+∠2+∠3+∠4= .
B.若Rt△ABC中,∠C=90°,∠A=42°,BC=3,则AC的边长为 .(用科学计算器计算,结果精确到0.01)
14.计算sin36°= (保留四个有效数字).
15.先用计算器求:cos20°≈ ,cos40°≈ ,cos60°= ,cos80°≈ .再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,连接起来: .归纳:在锐角范围内,余弦值,角大值 .
16.请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形过一个顶点有6条对角线,则这个多边形的边数是 .
B.用科学计算器计算:4sin44° .(精确到0.01)
三.解答题(共8小题)
17.用计算器求下列锐角的正弦、余弦和正切值(精确到0.0001):
(1)3°15′;
(2)68°6′.
18.已知锐角A的三角函数值,用科学计算器求∠A(结果精确到1').
(1)sinA=0.5018;
(2)cosA=0.7857;
(3)tanA=1.4036.
19.用科学计算器求下列各三角函数值(结果精确到0.0001):
(1)sin40°18';
(2)cos63°52'41″;
(3)tan52°6'.
20.用计算器求下列正切值对应的锐角θ,并填入下表:
tanθ 0.5 1 2 3 4 5 10 20 50
θ
21.用计算器求下列锐角三角比的值:
(1)sin53°49';
(2)sin30°4'56″;
(3)cos55';
(4)tan72°8″.
22.已知锐角α的三角函数值,用科学计算器求α(结果精确到1').
(1)sinα=0.5512;
(2)cosα=0.2559;
(3)tanα=2.755.
23.先利用计算器求出锐角α与β的度数,再比较它们的大小.
(1)cosα;
(2)sinα=0.4567,cosβ=0.5678.
24.(1)验证下列两组数值的关系:
2sin30° cos30°与sin60°;
2sin22.5° cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
1.3 三角函数的计算
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】先利用正弦的定义得到sinA=0.25,然后利用计算器求锐角∠A.
【解答】解:sinA0.25,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为
故选:A.
【点评】本题考查了计算器﹣三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
2.【答案】C
【分析】根据计算器的使用方法即可.
【解答】解:按照计算器的使用方法即可:先输入,2,再输入cos,再次输入55,最后再输入“=”即可.
故选:C.
【点评】本题考查计算器的使用方法,掌握计算器的使用方法是解题的关键.
3.【答案】A
【分析】直接根据计算器功能键判断.
【解答】解:根据计算器功能键,先按反三角2ndF,再按正切值.
故选:A.
【点评】本题考查利用计算器求角,熟悉计算器功能键和按键顺序是求解本题的关键.
4.【答案】D
【分析】根据正切的定义求解即可.
【解答】解:∵,
∴AC=BC tanB=8tan43°.
故选:D.
【点评】本题考查了正切的定义、计算器求三角函数等知识点,掌握是解题的关键.
5.【答案】C
【分析】根据计算器按键方法判断即可.
【解答】解:若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是.
故选:C.
【点评】此题考查了计算器﹣三角函数,以及度分秒的换算,弄清计算器上的按键方法是解本题的关键.
6.【答案】C
【分析】简单的电子计算器工作顺序是先输入者先算,其中R﹣CM表示存储、读出键,M+为存储加键,M﹣为存储减键,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【解答】解:利用该型号计算器计算cos55°,按键顺序正确的是.
故选:C.
【点评】本题主要考查了利用计算器求数的开方,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
7.【答案】B
【分析】先利用正弦的定义得到sinA=0.2,然后利用计算器求锐角∠A.
【解答】解:sinA0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
【点评】本题考查了锐角三角函数及计算器的应用,掌握科学计算器的应用是解决本题的关键.
8.【答案】D
【分析】根据用计算器算三角函数的方法:先按键“sin”,再输入角的度数,按键“=”即可得到结果.
【解答】解:先按键“sin”,再输入角的度数50,按键“=”即可得到结果.
故选:D.
【点评】本题考查了用计算器算三角函数的方法,牢记方法是关键.
9.【答案】D
【分析】根据锐角三角函数,可得sinA的值,根据计算器,可得A的值.
【解答】解:∵∠C=90°,a=5,c=13,
∴sinA0.385,
∠A≈22.64°=22°37′,
故选:D.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
10.【答案】D
【分析】根据正切的定义求出AC的表达式即可得出答案.
【解答】解:∵tan∠ABC,
∴AC=BC tan∠ABC=5tan26°,
故选:D.
【点评】本题考查了计算器,根据正切的定义求出AC的表达式是解题的关键.
二.填空题(共6小题)
11.【答案】见试题解答内容
【分析】熟练应用计算器,对计算器给出的结果,四舍五入法求近似数.
【解答】解:tan26°=9.654×0.4877=4.708≈4.71.
故答案为:4.71.
【点评】本题结合计算器的用法,旨在考查对基本概念的应用能力,需要同学们熟记近似数的精确度.
12.【答案】2.03.
【分析】先按“17”,再按“2ndF”键,再按“”键,再按“*”键,再按“tan”,再输入角度,最后按“=”即可得到结果.
【解答】解:tan38°15′≈2.03.
故答案为:2.03.
【点评】本题主要考查了计算器计算三角函数及立方根,属于基础题.
13.【答案】见试题解答内容
【分析】A.先求出∠A的外角,再根据多边形的外角和等于360度可求∠1+∠2+∠3+∠4;
B.根据正切函数可求AC的边长.
【解答】解:A.∵∠A=120°,
∴∠A的外角为180°﹣120°=60°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300°.
B.在Rt△ABC中,∠C=90°,∠A=42°,BC=3,
则AC=BC÷tan42°≈30.900≈3×2.449÷0.900≈8.16.
故答案为:300°;8.16.
【点评】考查了计算器﹣三角函数,多边形内角与外角,关键是熟悉多边形的外角和等于360度的知识点,以及熟练掌握计算器的使用方法.
14.【答案】见试题解答内容
【分析】sin36°≈0.587785252,保留四个有效数字,从左边第一个不是0的数字起,第五个数是8,根据四舍五入法,结果为0.5878.
【解答】解:∵sin36°≈0.587785252
保留四个有效数字为sin36°=0.5878.
故答案为:0.5878.
【点评】本题考查了运用计算器的能力及对有效数字的概念的掌握情况.
15.【答案】0.9397,0.7660,0.5,0.1736;cos20°>cos40°>cos60°;小.
【分析】利用计算器依次输入,即可得到结果.
【解答】解:利用计算器依次输入得到结果为:cos20°≈0.9397,cos40°≈0.7660,cos60°=0.5,cos80°≈.0.1736;故把cos20°,cos40°,cos60°可以用>连接为:把cos20°>cos40°>cos60°;由题可知在锐角范围内,余弦值,角大值小.
故答案为:0.9397,0.7660,0.5,0.1736;cos20°>cos40°>cos60°;小.
【点评】本题考查计算器的用法,掌握计算器的用法便可解决问题.
16.【答案】见试题解答内容
【分析】A、根据从每一个顶点处可以作的对角线的条数为(n﹣3)计算即可得解.
B、利用计算器计算出和sin44°,然后进行实数运算,最后精确到0.01.
【解答】解:A、∵多边形从每一个顶点出发都有6条对角线,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故答案为:九.
B、4sin44°4×0.6947﹣4.1231≈﹣1.34.
故答案为:﹣1.34.
【点评】本题考查了多边形的对角线公式,熟记从每一个顶点处可以作的对角线的条数为(n﹣3)是解题的关键.
三.解答题(共8小题)
17.【答案】见解答.
【分析】根据计算器的使用方法进行解题即可.
【解答】解:(1)sin3°15′≈0.0567,cos3°15′≈0.9984,tan3°15′≈0.0568;
(2)sin68°6′≈0.9278,cos68°6′≈0.3730,tan68°6′≈2.4876.
【点评】本题考查计算的使用和近似数和有效数字,熟练掌握相关的知识点是解题的关键.
18.【答案】(1)∠A≈30°7′;
(2)∠A≈38°13′;
(3)∠A≈54°32′.
【分析】用计算器直接计算即可.
【解答】解:(1)∠A≈30°7′;
(2)∠A≈38°13′;
(3)∠A≈54°32′.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
19.【答案】(1)sin40°18'≈0.6468;
(2)cos63°52'41″≈0.4403;
(3)tan52°6'≈1.2846.
【分析】用计算器直接计算即可.
【解答】解:(1)sin40°18'≈0.6468;
(2)cos63°52'41″≈0.4403;
(3)tan52°6'≈1.2846.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
20.【答案】26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
【分析】用计算器直接计算即可.
【解答】解:对应的锐角θ依次为:26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
故答案为:26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
【点评】本题考查的是用计算器求锐角的度数,关键在于熟练使用计算器.
21.【答案】(1)sin53°49'≈0.80713;
(2)sin30°4'56″≈0.50124;
(3)cos55'≈0.99987;
(4)tan72°8″≈3.0781.
【分析】用计算器直接计算即可.
【解答】解:(1)sin53°49'≈0.80713;
(2)sin30°4'56″≈0.50124;
(3)cos55'≈0.99987;
(4)tan72°8″≈3.0781.
【点评】本题考查了使用计算器求三角函数值,关键是熟练使用计算器.
22.【答案】(1)α≈33°27′;
(2)α≈75°10′:
(3)α≈70°3′.
【分析】用计算器直接计算即可.
【解答】解:用科学计算器解得:
(1)α≈33°27′;
(2)α≈75°10′:
(3)α≈70°3′.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
23.【答案】(1)∠α<∠β;
(2)∠α<∠β.
【分析】用计算器分别求出锐角α与β的度数,再比较它们的大小即可解决问题.
【解答】解:(1)∵cosα,
∴∠α≈41.41°,∠β≈51.34°,
∴∠α<∠β;
(2)∵sinα=0.4567,cosβ=0.5678,
∴∠α≈27.2°,∠β≈55.4°,
∴∠α<∠β.
【点评】本题主要考查已知三角函数值用计算器求角的度数,熟练掌握用计算器求角的度数的方法是解决问题的关键.
24.【答案】见试题解答内容
【分析】(1)分别计算出各数,进而可得出结论;
(2)根据(1)中的关系可得出结论;
(3)任选一个角验证(3)的结论即可;
(4)用α表示一个锐角,写出这个关系式即可.
【解答】解:(1)∵2sin30° cos30°=2,sin60°.
2sin22.5° cos22.5≈2×0.38×0.92≈0.7,sin45°0.7,
∴2sin30° cos30°=sin60°,2sin22.5° cos22.5=sin45°;
(2)由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)2sin15° cos15°≈2×0.26×0.97,sin30°;
故结论成立;
(4)2sinα cosα=sin2α.
【点评】本题考查的是三角函数,根据题意找出规律是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3 三角函数的计算
一.选择题(共10小题)
1.为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A.
B.
C.
D.
2.利用计算器计算cos55°,下列按键顺序正确的是( )
A.
B.
C.
D.
3.已知tanA=0.85,用计算器求∠A的大小,下列按键顺序正确的是( )
A.
B.
C.
D.
4.如图,在△ABC中,∠C=90°,∠B=43°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A. B.
C. D.
5.若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是( )
A.
B.
C.
D.
6.如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算cos55°,按键顺序正确的是( )
A.
B.
C.
D.
7.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
8.用计算器求sin50°的值,按键顺序是( )
A. B.
C. D.
9.在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于( )(精确到1′)
A.28°38′ B.65°22′ C.67°23′ D.22°37′
10.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
二.填空题(共6小题)
11.用科学计算器计算:tan26°= .(结果精确到0.01)
12.tan38°15′≈ (结果精确到0.01).
13.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,∠1、∠2、∠3、∠4是五边形ABCDE的四个角,若∠A=120°,则∠1+∠2+∠3+∠4= .
B.若Rt△ABC中,∠C=90°,∠A=42°,BC=3,则AC的边长为 .(用科学计算器计算,结果精确到0.01)
14.计算sin36°= (保留四个有效数字).
15.先用计算器求:cos20°≈ ,cos40°≈ ,cos60°= ,cos80°≈ .再按从大到小的顺序用“>”把cos20°,cos40°,cos60°,连接起来: .归纳:在锐角范围内,余弦值,角大值 .
16.请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形过一个顶点有6条对角线,则这个多边形的边数是 .
B.用科学计算器计算:4sin44° .(精确到0.01)
三.解答题(共8小题)
17.用计算器求下列锐角的正弦、余弦和正切值(精确到0.0001):
(1)3°15′;
(2)68°6′.
18.已知锐角A的三角函数值,用科学计算器求∠A(结果精确到1').
(1)sinA=0.5018;
(2)cosA=0.7857;
(3)tanA=1.4036.
19.用科学计算器求下列各三角函数值(结果精确到0.0001):
(1)sin40°18';
(2)cos63°52'41″;
(3)tan52°6'.
20.用计算器求下列正切值对应的锐角θ,并填入下表:
tanθ 0.5 1 2 3 4 5 10 20 50
θ
21.用计算器求下列锐角三角比的值:
(1)sin53°49';
(2)sin30°4'56″;
(3)cos55';
(4)tan72°8″.
22.已知锐角α的三角函数值,用科学计算器求α(结果精确到1').
(1)sinα=0.5512;
(2)cosα=0.2559;
(3)tanα=2.755.
23.先利用计算器求出锐角α与β的度数,再比较它们的大小.
(1)cosα;
(2)sinα=0.4567,cosβ=0.5678.
24.(1)验证下列两组数值的关系:
2sin30° cos30°与sin60°;
2sin22.5° cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
1.3 三角函数的计算
参考答案与试题解析
一.选择题(共10小题)
1.【答案】A
【分析】先利用正弦的定义得到sinA=0.25,然后利用计算器求锐角∠A.
【解答】解:sinA0.25,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为
故选:A.
【点评】本题考查了计算器﹣三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
2.【答案】C
【分析】根据计算器的使用方法即可.
【解答】解:按照计算器的使用方法即可:先输入,2,再输入cos,再次输入55,最后再输入“=”即可.
故选:C.
【点评】本题考查计算器的使用方法,掌握计算器的使用方法是解题的关键.
3.【答案】A
【分析】直接根据计算器功能键判断.
【解答】解:根据计算器功能键,先按反三角2ndF,再按正切值.
故选:A.
【点评】本题考查利用计算器求角,熟悉计算器功能键和按键顺序是求解本题的关键.
4.【答案】D
【分析】根据正切的定义求解即可.
【解答】解:∵,
∴AC=BC tanB=8tan43°.
故选:D.
【点评】本题考查了正切的定义、计算器求三角函数等知识点,掌握是解题的关键.
5.【答案】C
【分析】根据计算器按键方法判断即可.
【解答】解:若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是.
故选:C.
【点评】此题考查了计算器﹣三角函数,以及度分秒的换算,弄清计算器上的按键方法是解本题的关键.
6.【答案】C
【分析】简单的电子计算器工作顺序是先输入者先算,其中R﹣CM表示存储、读出键,M+为存储加键,M﹣为存储减键,根据按键顺序写出式子,再根据开方运算即可求出显示的结果.
【解答】解:利用该型号计算器计算cos55°,按键顺序正确的是.
故选:C.
【点评】本题主要考查了利用计算器求数的开方,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
7.【答案】B
【分析】先利用正弦的定义得到sinA=0.2,然后利用计算器求锐角∠A.
【解答】解:sinA0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
【点评】本题考查了锐角三角函数及计算器的应用,掌握科学计算器的应用是解决本题的关键.
8.【答案】D
【分析】根据用计算器算三角函数的方法:先按键“sin”,再输入角的度数,按键“=”即可得到结果.
【解答】解:先按键“sin”,再输入角的度数50,按键“=”即可得到结果.
故选:D.
【点评】本题考查了用计算器算三角函数的方法,牢记方法是关键.
9.【答案】D
【分析】根据锐角三角函数,可得sinA的值,根据计算器,可得A的值.
【解答】解:∵∠C=90°,a=5,c=13,
∴sinA0.385,
∠A≈22.64°=22°37′,
故选:D.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
10.【答案】D
【分析】根据正切的定义求出AC的表达式即可得出答案.
【解答】解:∵tan∠ABC,
∴AC=BC tan∠ABC=5tan26°,
故选:D.
【点评】本题考查了计算器,根据正切的定义求出AC的表达式是解题的关键.
二.填空题(共6小题)
11.【答案】见试题解答内容
【分析】熟练应用计算器,对计算器给出的结果,四舍五入法求近似数.
【解答】解:tan26°=9.654×0.4877=4.708≈4.71.
故答案为:4.71.
【点评】本题结合计算器的用法,旨在考查对基本概念的应用能力,需要同学们熟记近似数的精确度.
12.【答案】2.03.
【分析】先按“17”,再按“2ndF”键,再按“”键,再按“*”键,再按“tan”,再输入角度,最后按“=”即可得到结果.
【解答】解:tan38°15′≈2.03.
故答案为:2.03.
【点评】本题主要考查了计算器计算三角函数及立方根,属于基础题.
13.【答案】见试题解答内容
【分析】A.先求出∠A的外角,再根据多边形的外角和等于360度可求∠1+∠2+∠3+∠4;
B.根据正切函数可求AC的边长.
【解答】解:A.∵∠A=120°,
∴∠A的外角为180°﹣120°=60°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300°.
B.在Rt△ABC中,∠C=90°,∠A=42°,BC=3,
则AC=BC÷tan42°≈30.900≈3×2.449÷0.900≈8.16.
故答案为:300°;8.16.
【点评】考查了计算器﹣三角函数,多边形内角与外角,关键是熟悉多边形的外角和等于360度的知识点,以及熟练掌握计算器的使用方法.
14.【答案】见试题解答内容
【分析】sin36°≈0.587785252,保留四个有效数字,从左边第一个不是0的数字起,第五个数是8,根据四舍五入法,结果为0.5878.
【解答】解:∵sin36°≈0.587785252
保留四个有效数字为sin36°=0.5878.
故答案为:0.5878.
【点评】本题考查了运用计算器的能力及对有效数字的概念的掌握情况.
15.【答案】0.9397,0.7660,0.5,0.1736;cos20°>cos40°>cos60°;小.
【分析】利用计算器依次输入,即可得到结果.
【解答】解:利用计算器依次输入得到结果为:cos20°≈0.9397,cos40°≈0.7660,cos60°=0.5,cos80°≈.0.1736;故把cos20°,cos40°,cos60°可以用>连接为:把cos20°>cos40°>cos60°;由题可知在锐角范围内,余弦值,角大值小.
故答案为:0.9397,0.7660,0.5,0.1736;cos20°>cos40°>cos60°;小.
【点评】本题考查计算器的用法,掌握计算器的用法便可解决问题.
16.【答案】见试题解答内容
【分析】A、根据从每一个顶点处可以作的对角线的条数为(n﹣3)计算即可得解.
B、利用计算器计算出和sin44°,然后进行实数运算,最后精确到0.01.
【解答】解:A、∵多边形从每一个顶点出发都有6条对角线,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故答案为:九.
B、4sin44°4×0.6947﹣4.1231≈﹣1.34.
故答案为:﹣1.34.
【点评】本题考查了多边形的对角线公式,熟记从每一个顶点处可以作的对角线的条数为(n﹣3)是解题的关键.
三.解答题(共8小题)
17.【答案】见解答.
【分析】根据计算器的使用方法进行解题即可.
【解答】解:(1)sin3°15′≈0.0567,cos3°15′≈0.9984,tan3°15′≈0.0568;
(2)sin68°6′≈0.9278,cos68°6′≈0.3730,tan68°6′≈2.4876.
【点评】本题考查计算的使用和近似数和有效数字,熟练掌握相关的知识点是解题的关键.
18.【答案】(1)∠A≈30°7′;
(2)∠A≈38°13′;
(3)∠A≈54°32′.
【分析】用计算器直接计算即可.
【解答】解:(1)∠A≈30°7′;
(2)∠A≈38°13′;
(3)∠A≈54°32′.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
19.【答案】(1)sin40°18'≈0.6468;
(2)cos63°52'41″≈0.4403;
(3)tan52°6'≈1.2846.
【分析】用计算器直接计算即可.
【解答】解:(1)sin40°18'≈0.6468;
(2)cos63°52'41″≈0.4403;
(3)tan52°6'≈1.2846.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
20.【答案】26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
【分析】用计算器直接计算即可.
【解答】解:对应的锐角θ依次为:26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
故答案为:26.6°,45°,63.4°,71.6°,76°,78.7°,84.3°,87.1°,88.9°;
【点评】本题考查的是用计算器求锐角的度数,关键在于熟练使用计算器.
21.【答案】(1)sin53°49'≈0.80713;
(2)sin30°4'56″≈0.50124;
(3)cos55'≈0.99987;
(4)tan72°8″≈3.0781.
【分析】用计算器直接计算即可.
【解答】解:(1)sin53°49'≈0.80713;
(2)sin30°4'56″≈0.50124;
(3)cos55'≈0.99987;
(4)tan72°8″≈3.0781.
【点评】本题考查了使用计算器求三角函数值,关键是熟练使用计算器.
22.【答案】(1)α≈33°27′;
(2)α≈75°10′:
(3)α≈70°3′.
【分析】用计算器直接计算即可.
【解答】解:用科学计算器解得:
(1)α≈33°27′;
(2)α≈75°10′:
(3)α≈70°3′.
【点评】本题考查的是用计算器求三角函数值,关键在于熟练使用计算器.
23.【答案】(1)∠α<∠β;
(2)∠α<∠β.
【分析】用计算器分别求出锐角α与β的度数,再比较它们的大小即可解决问题.
【解答】解:(1)∵cosα,
∴∠α≈41.41°,∠β≈51.34°,
∴∠α<∠β;
(2)∵sinα=0.4567,cosβ=0.5678,
∴∠α≈27.2°,∠β≈55.4°,
∴∠α<∠β.
【点评】本题主要考查已知三角函数值用计算器求角的度数,熟练掌握用计算器求角的度数的方法是解决问题的关键.
24.【答案】见试题解答内容
【分析】(1)分别计算出各数,进而可得出结论;
(2)根据(1)中的关系可得出结论;
(3)任选一个角验证(3)的结论即可;
(4)用α表示一个锐角,写出这个关系式即可.
【解答】解:(1)∵2sin30° cos30°=2,sin60°.
2sin22.5° cos22.5≈2×0.38×0.92≈0.7,sin45°0.7,
∴2sin30° cos30°=sin60°,2sin22.5° cos22.5=sin45°;
(2)由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)2sin15° cos15°≈2×0.26×0.97,sin30°;
故结论成立;
(4)2sinα cosα=sin2α.
【点评】本题考查的是三角函数,根据题意找出规律是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
