2.4 二次函数的应用(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学九年级下册
文档属性
| 名称 | 2.4 二次函数的应用(巩固复习.培优卷.含解析)-2024-2025学年北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 15:30:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.4 二次函数的应用
一.选择题(共10小题)
1.如图,要修建一个圆形喷水池,在池中心O点竖直安装一根水管,在水管的顶端A处安一个喷水头,使喷出的抛物线形水柱在与池中心O点的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心O点3m.则水管OA的高是( )
A.2m B.2.25m C.2.5m D.2.8m
2.把一个足球垂直于水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤3).若存在两个不同的t的值,使足球离地面的高度均为a米,则a的取值范围是( )
A.0≤a≤15 B.0≤a<20 C.15≤a<20 D.15≤a≤20
3.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段OA表示水平的路面,以O为坐标原点OA所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量OA=12m,抛物线的顶点P到OA的距离为5m,则抛物线的函数表达式为( )
A. B.
C. D.
4.在一个边长为5的正方形中挖去一个边长为x(0<x<5)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )
A.y=x2 B.y=25﹣x2 C.y=x2﹣25 D.y=25﹣2x
5.将进货单价为90元的某种商品按100元售出时,能卖出500个,单价每上涨1元,其销售量就减小10个,为了获得最大利润,售价应定为每件( )
A.110元 B.120元 C.130元 D.150元
6.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件,要使利润最大,每件的售价应为( )
A.24元 B.25元 C.28元 D.30元
7.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:①AB=30m;②池底所在抛物线的解析式为;③若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为1.2m;④池塘最深处到水面CD的距离为3.2m;其中结论错误的是( )
A.① B.② C.③ D.④
8.用40cm的绳子围成一个矩形,则矩形面积ycm2与一边长为xcm之间的函数关系式为( )
A.y=x2 B.y=﹣x2+40x C.y=﹣x2+20x D.y=﹣x2+20
9.已知多项式A=x2﹣3x+1+n,B=ax2+2x+b(a≠0).
①当n=0时,若A=0,则;
②当n=0,b=0时,若对任意的实数x都有A+B≥0,则a的取值范围为a>﹣1;
③当,a=1,b=6时,的最小值为.
以上说法正确的个数是( )
A.0 B.1 C.2 D.3
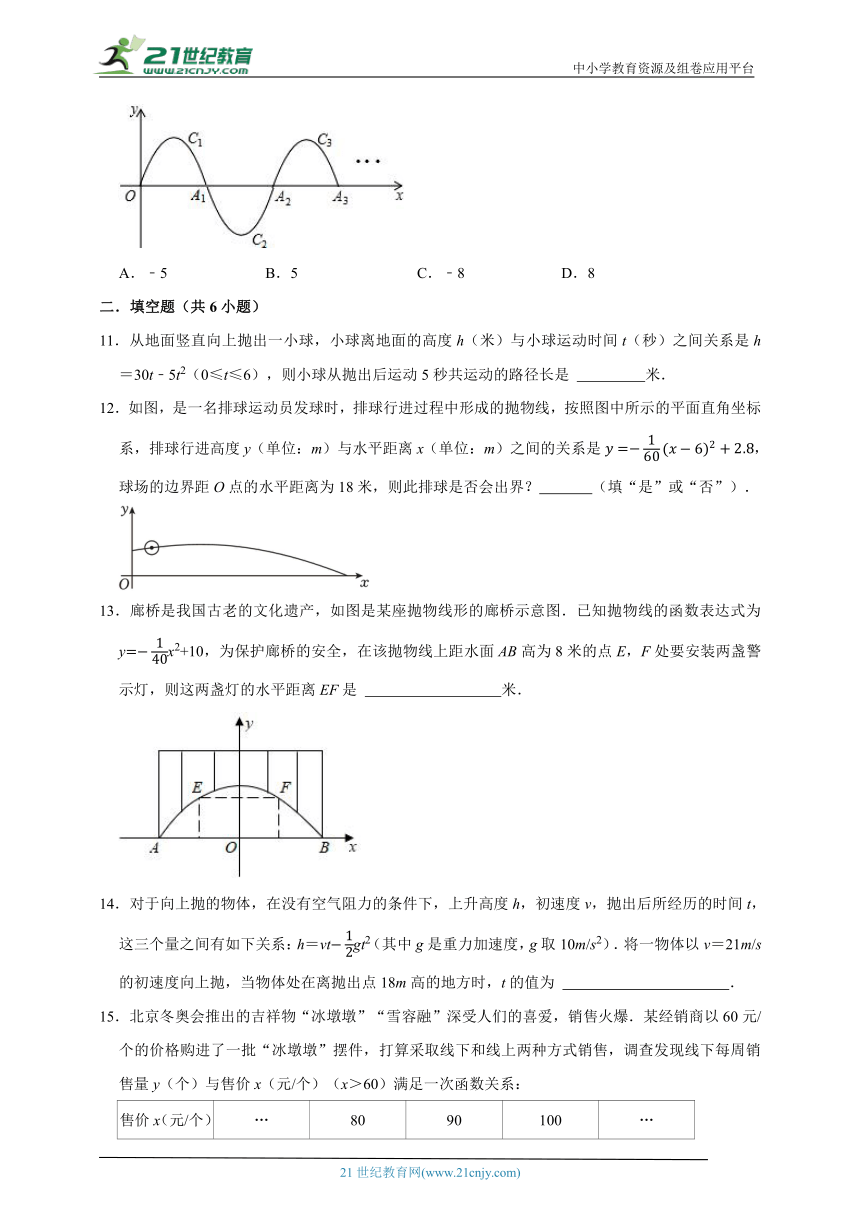
10.如图,一段抛物线y=﹣x2+6x(0≤x≤6),记为抛物线C1,它与x轴交于点O、A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3,…如此进行下去,得到一条“波浪线”,若点M(2021,m)在此“波浪线”上,则m的值为( )
A.﹣5 B.5 C.﹣8 D.8
二.填空题(共6小题)
11.从地面竖直向上抛出一小球,小球离地面的高度h(米)与小球运动时间t(秒)之间关系是h=30t﹣5t2(0≤t≤6),则小球从抛出后运动5秒共运动的路径长是 米.
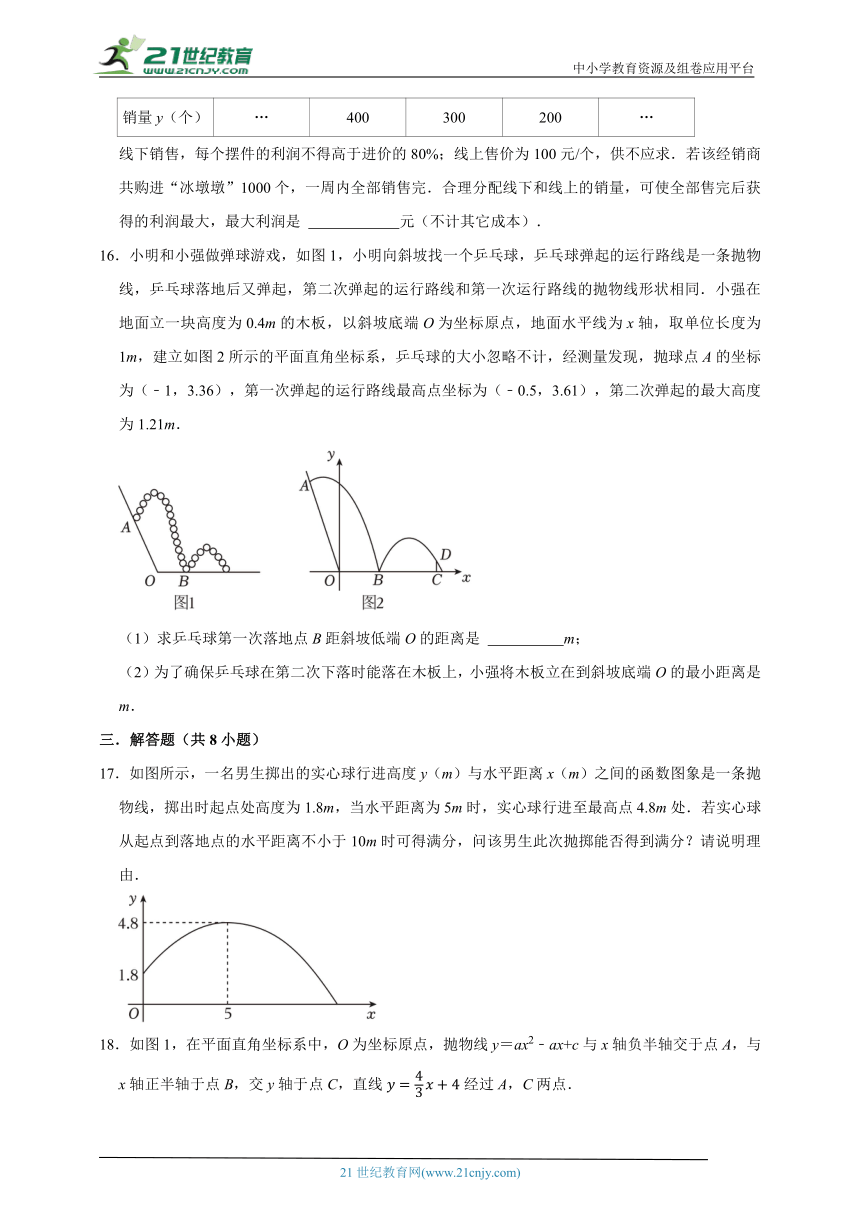
12.如图,是一名排球运动员发球时,排球行进过程中形成的抛物线,按照图中所示的平面直角坐标系,排球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,球场的边界距O点的水平距离为18米,则此排球是否会出界? (填“是”或“否”).
13.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为yx2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
14.对于向上抛的物体,在没有空气阻力的条件下,上升高度h,初速度v,抛出后所经历的时间t,这三个量之间有如下关系:h=vtgt2(其中g是重力加速度,g取10m/s2).将一物体以v=21m/s的初速度向上抛,当物体处在离抛出点18m高的地方时,t的值为 .
15.北京冬奥会推出的吉祥物“冰墩墩”“雪容融”深受人们的喜爱,销售火爆.某经销商以60元/个的价格购进了一批“冰墩墩”摆件,打算采取线下和线上两种方式销售,调查发现线下每周销售量y(个)与售价x(元/个)(x>60)满足一次函数关系:
售价x(元/个) … 80 90 100 …
销量y(个) … 400 300 200 …
线下销售,每个摆件的利润不得高于进价的80%;线上售价为100元/个,供不应求.若该经销商共购进“冰墩墩”1000个,一周内全部销售完.合理分配线下和线上的销量,可使全部售完后获得的利润最大,最大利润是 元(不计其它成本).
16.小明和小强做弹球游戏,如图1,小明向斜坡找一个乒乓球,乒乓球弹起的运行路线是一条抛物线,乒乓球落地后又弹起,第二次弹起的运行路线和第一次运行路线的抛物线形状相同.小强在地面立一块高度为0.4m的木板,以斜坡底端O为坐标原点,地面水平线为x轴,取单位长度为1m,建立如图2所示的平面直角坐标系,乒乓球的大小忽略不计,经测量发现,抛球点A的坐标为(﹣1,3.36),第一次弹起的运行路线最高点坐标为(﹣0.5,3.61),第二次弹起的最大高度为1.21m.
(1)求乒乓球第一次落地点B距斜坡低端O的距离是 m;
(2)为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端O的最小距离是 m.
三.解答题(共8小题)
17.如图所示,一名男生掷出的实心球行进高度y(m)与水平距离x(m)之间的函数图象是一条抛物线,掷出时起点处高度为1.8m,当水平距离为5m时,实心球行进至最高点4.8m处.若实心球从起点到落地点的水平距离不小于10m时可得满分,问该男生此次抛掷能否得到满分?请说明理由.
18.如图1,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣ax+c与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,直线经过A,C两点.
(1)求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,PD∥AC交y轴于点D,若设线段PD的长为d,点P的横坐标为t,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,连接AD,点E为抛物线上第四象限上一点,AD=AE,连接CE交x轴于点F,若∠ACE+∠ADE=180°,求点P的横坐标.
19.某水果店以8元/kg的价钱购进了一批水果,已知当售价为14元/kg时,每天可卖出40kg,为了扩大销售,增加盈利,同时优惠顾客,该水果店决定对该种水果降价销售.经调查发现,售价每千克降低1元时,则可多售出20kg.
(1)若要该水果店每天销售该种水果的利润达到300元,则该种水果的售价应定为多少元?
(2)若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为多少元?
20.金沙意米是仙游县著名的土特产、它品质优异,荣获国家地理标志证明商标,某超市销售的金沙意米,成本价为每千克22元,超市限定售价不高于每千克34元.销售中平均每天销售量y(kg)与销售单价x(元)的关系可以近似地看作一次函数,如表所示:
x 26 28 30 32
y 70 60 50 40
(1)求出y与x之间的函数关系式;
(2)设超市每天销售意米的利润为w(元),求w与x之间的函数关系式,当x取何值时,w的值达到最大?最大值是多少?
21.如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
22.足球作为一项重要的体育运动,越来越受到广大体育爱好者的喜欢,校园足球更是同学们的最爱.在一次足球训练中,小王从球门正前方9米的A处射门,球射向球门的路线呈抛物线形.当球飞行的水平距离为6米时,球达到最高点D,此时球离地面4米.已知球门BC的高为2.44米,现以O为原点建立如图所示的平面直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,请通过计算说明当时小王应该带球向正后方移动多少米射门,才能让足球经过B点正上方米处入门?
23.某一抛物线形隧道,一侧建有垂直于地面的隔离墙,其横截面如图所示,并建立平面直角坐标系.已知抛物线经过(0,3),,三点.
(1)求抛物线的解析式(不考虑自变量的取值范围);
(2)有一辆高5m,顶部宽4m的工程车要通过该隧道,该车能否正常通过?并说明理由;
(3)现准备在隧道上A处安装一个直角形钢架BAC,对隧道进行维修.B,C两点分别在隔离墙和地面上,且AB与隔离墙垂直,AC与地面垂直,求钢架BAC的最大长度.
24.足球训练中球员从球门正前方8米的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米.现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)已知球门高OB为2.44米,通过计算判断球能否射进球门(忽略其他因素);
(3)已知点C为OB上一点,OC=2.25米,若射门路线的形状、最大高度均保持不变,当时球员带球向正后方移动n米再射门,足球恰好经过OC区域(含点O和C),求n的取值范围.
2.4 二次函数的应用
参考答案与试题解析
一.选择题(共10小题)
1.【答案】B
【分析】利用顶点式求得抛物线的解析式,再令x=0,求得相应的函数值,即为所求的答案.
【解答】解:由题意可知点(1,3)是抛物线的顶点,
∴设这段抛物线的解析式为y=a(x﹣1)2+3.
∵该抛物线过点(3,0),
∴0=a(3﹣1)2+3,
解得:a.
∴y(x﹣1)2+3.
∵当x=0时,y(0﹣1)2+332.25,
∴水管应长2.25m.
故选:B.
【点评】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法及二次函数的相关性质是解题的关键.
2.【答案】C
【分析】由题意可得方程a=20t﹣5t2,存在两个不同的t的值,使足球离地面的高度均为a,故Δ=b2﹣4ac>0,即可求出相应的范围.
【解答】解:由题意得方程a=20t﹣5t2,有两个不相等的实根
∴Δ=b2﹣4ac>0,即202﹣4×5a>0
∴0≤a<20
又∵0≤t≤3
∴当t=3时,a=20×3﹣5×32=60﹣45=15,
所以a的取值范围为:15≤a<20,
故选:C.
【点评】本题主要考查二次函数的应用,解题的关键是根据题意得到相应的方程及将实际问题转化为方程问题.
3.【答案】D
【分析】由OA的长度及点P到OA的距离,可得出点P的坐标,设出抛物线的顶点式,利用待定系数法,即可求出抛物线的函数表达式.
【解答】解:∵OA=12m,抛物线的顶点P到OA的距离为5m,
∴抛物线顶点P的坐标为(6,5),
设抛物线的函数表达式为y=a(x﹣6)2+5,
将O(0,0)代入y=a(x﹣6)2+5得:0=36a+5,
解得:a,
∴抛物线的函数表达式为y(x﹣6)2+5,
故选:D.
【点评】本题考查了待定系数法求二次函数解析式,根据给定点的坐标,利用待定系数法求出二次函数解析式是解题的关键.
4.【答案】B
【分析】利用剩余部分的面积=大正方形的面积﹣小正方形的面积,即可找出y关于x的函数解析式.
【解答】解:根据题意得:y=52﹣x2,
∴y关于x的函数解析式是y=25﹣x2.
故选:B.
【点评】本题考查了根据实际问题列二次函数关系式,根据各数量之间的关系,找出y关于x的函数解析式是解题的关键.
5.【答案】B
【分析】设售价上涨x元,利润y元,根据将进货价为90元的某种商品按100元出售时,能卖出500个,商品每个上涨1元,其销售量就减少10个,则售价为(100+x)元,销售量为(500﹣10x)个,可列出二次函数解析式,把二次函数解析式化为顶点式即可求得结果.
【解答】解:设在售价100元的基础上涨价x元,获总利润y元,
则y=(100+x﹣90)(500﹣10x)=﹣10(x﹣20)2+9000,
所以x=20时,y值最大,
所以售价应定为120元,
故选:B.
【点评】本题主要考查了二次函数的应用,能够求出二次函数解析式是解决问题的关键.
6.【答案】B
【分析】设利润为w根据利润等于利润单价乘以数量列出函数,根据函数性质求解即可得到答案.
【解答】解:设利润为w 元,
由题意可得,w=(x﹣20)(30﹣x)=﹣x2+50x﹣600=﹣(x﹣25)2+25,
∵﹣1<0,20≤x≤30,
∴当x=25时w最大,
故选:B.
【点评】本题考查二次函数解决销售利润问题中最值问题,解题的关键是列出函数根据函数性质求解.
7.【答案】C
【分析】根据图象可以判断①;设出池底所在抛物线的解析式为y=ax2﹣5,再把(15,0)代入解析式求出a即可判断②;把x=12代入解析式求出y=﹣1.8,再用5﹣1.8即可判断③;把x=6代入解析式即可判断④.
【解答】解:①观察图形可知,AB=30m,
故①正确;
②设池底所在抛物线的解析式为y=ax2﹣5,
将(15,0)代入,可得a,
故抛物线的解析式为yx2﹣5;
故②正确;
③当池塘中水面的宽度减少为原来的一半,即水面宽度为12m时,
将x=6代入yx2﹣5,得y=﹣4.2,
可知此时最深处到水面的距离为5﹣4.2=0.8(m),
即为原来的,
故③错误;
④∵yx2﹣5,
∴当x=12时,y=﹣1.8,
故池塘最深处到水面CD的距离为5﹣1.8=3.2(m),
故④正确.
故选:C.
【点评】本题考查了二次函数的应用,体现了数学建模、数学抽象、数学运算素养.
8.【答案】C
【分析】先根据矩形一边长为xcm,周长为40cm得出另一边长为20﹣x(cm),再根据矩形的面积公式可得答案.
【解答】解:∵矩形一边长为xcm,周长为40cm,
∴另一边长为20﹣x(cm),
∴矩形的面积y=x(20﹣x)=﹣x2+20x,
故选:C.
【点评】本题主要考查根据实际问题列出二次函数关系式,根据实际问题确定二次函数关系式关键是读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数图象要根据自变量的取值范围来确定.
9.【答案】B
【分析】由当n=0时,A=0,得x2﹣3x+1=0,可得x3,故(x)2=9,从而x27,判断①错误;当n=0,b=0时,对任意的实数x都有A+B≥0,可知(a+1)x2﹣x+1≥0对任意x均成立;即抛物线y=(a+1)x2﹣x+1在x轴上或x轴的上方;故,可得得a,判断②错误;当,a=1,b=6时,,可看作x轴上的点(x,0)到点(,)及点(﹣1,)的距离之和,即可知当点(x,0),点(,)及点(﹣1,)共线时,取最小值,的最小值为,判断③正确.
【解答】解:根据题意得:x2﹣3x+1=0,此时x≠0,
∴x2+1=3x可得x3,
∴(x)2=9,
∴x27,故①错误;
∵当n=0,b=0时,对任意的实数x都有A+B≥0,
∴x2﹣3x+1+ax2+2x≥0,
即(a+1)x2﹣x+1≥0对任意x均成立;
∴抛物线y=(a+1)x2﹣x+1在x轴上或x轴的上方;
∴a+1>0且Δ<0,
∴,
解得a,故②错误;
当,a=1,b=6时,A=x2﹣3x,B=x2+2x+6,
∴
,
而可看作x轴上的点(x,0)到点(,)及点(﹣1,)的距离之和,
∴当点(x,0),点(,)及点(﹣1,)共线时,取最小值,最小值即为点(,)和点(﹣1,)之间的距离,
∴的最小值为,故③正确;
∴正确的有③,共1个;
故选:B.
【点评】本题考查二次函数的应用,两点间的距离公式的应用,完全平方公式的应用等知识,解题的关键是灵活掌握二次函数与二次不等式的关系及两点间的距离公式.
10.【答案】B
【分析】根据y=﹣x2+6x(0≤x≤6)可以得到:整个函数图象每隔6×2=12个单位长度,函数值就相等,而2021=12×168+5,由此即可计算.
【解答】解:∵y=﹣x2+6x=﹣x(x﹣6)(0≤x≤6),
∴A1(6,0),
∴整个函数图象每隔6×2=12个单位长度,函数值就相等,
∵2021=12×168+5,
所以m的值等于x=5时的纵坐标,
所以m=﹣52+6×5=5.
故选:B.
【点评】本题考查了抛物线与x轴的交点,二次函数的性质,二次函数与几何变换,解决此题的关键在于能根据函数图象发现规律:m的值等于x=5时的纵坐标.
二.填空题(共6小题)
11.【答案】65.
【分析】根据题目中的函数解析式可以求得h的最大值,从而可以求得小球从抛出后运动5秒共运动的路径长,本题得以解决.
【解答】解:∵h=30t﹣5t2=﹣5(t﹣3)2+45(0≤t≤6),
当t=3时,h取得最大值,此时h=45,
当t=5时,h=25,
∴小球从抛出后运动5秒共运动的路径长是:45+(45﹣25)=65(米),
故答案为:65.
【点评】本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的总的路径的长.
12.【答案】见试题解答内容
【分析】令y=0,解方程求出相应的x的值,与18比较即可.
【解答】解:令y=0,则(x﹣6)2+2.8=0,
解得x1=6+2,x2=6﹣2(舍去),
∵6+218,
∴此排球是会出界,
故答案为:是.
【点评】本题考查二次函数的应用,解答本题的关键是求出抛物线与x轴正半轴的交点的横坐标的值.
13.【答案】见试题解答内容
【分析】令y=8,即yx2+10=8,求出x值,进而求解.
【解答】解:令y=8,即yx2+10=8,
解得:x=±4,
∴则EF=4(﹣4)=8(米).
【点评】本题考查的是二次函数在实际生活中的应用,解题的关键是弄懂题意,该题比较简单.
14.【答案】或3.
【分析】把v=21,h=18代入h=vtgt2得一元二次方程,求解即可.
【解答】解:把v=21,h=18代入h=vtgt2得,
18=21t10t2,
整理得:5t2﹣21t+18=0,
解得t1,t2=3,
∴当物体处在离抛出点18m高的地方时,t的值为或3.
故答案为:或3.
【点评】此题主要考查了二次函数的应用以及一元二次方程的解法,正确把已知数据代入是解题关键.
15.【答案】40960.
【分析】根据总利润=线下销售利润+线上销售利润列出函数解析式找最值.
【解答】解:设y与x的函数表达式为y=kx+b,代入得:
,
解得:,
∴y与x的函数表达式为 y=﹣10x+1200,
当线下销量为(﹣10x+1200))个时,线上销量为1000﹣(﹣10x+1200)=(10x﹣200)个,
设全部售完后获得的利润为w元,根据题意得:
w=(x﹣60)(﹣10x+1200)+(100﹣60)(10x﹣200)
=﹣10x2+2200x﹣80000
=﹣10(x﹣110)2+41000,
∵线下销售,每个摆件的利润不得高于进价的80%,
∴x﹣60≤60×80,
解得:x≤108,
∵﹣10<0,对称轴为x=110,
∴当x=108时,w有最大值,最大值为40960元,
故答案为:40960.
【点评】本题考查了二次函数的应用和待定系数法求函数解析式,关键是设出y与x的函数表达式为y=kx+b,然后用待定系数法求函数解析式即可.
16.【答案】(1)1.4;(2)3.4.
【分析】(1)依据题意,根据已知条件设出抛物线的顶点式解析式,再把A点坐标代入解析式求出a即可得出解析式,然后令y=0,解方程求出x即可;
(2)依据题意,用待定系数法求出乒乓球第二次弹起运行路线的抛物线解析式,再令y=0和y=0.4,进而可以判断得解.
【解答】解:(1)由题意得,乒乓球第一次弹起运行路线的抛物线顶点为 (﹣0.5,3.61),过点A(﹣1,3.36),
设乒乓球第一次弹起运行路线的抛物线解析式为y1=a(x+0.5)2+3.61,
代入A(﹣1,3.36)得:3.36=a(﹣1+0.5)2+3.61,
解得 a=﹣1,
∴乒乓球第一次弹起运行路线的抛物线解析式为y1=﹣(x+0.5)2+3.61=﹣x2﹣x+3.36.
令 y1=0,
∴﹣(x+0.5)2+3.61=0.
∴解得 x1=1.4,x2=﹣2.4 (舍).
∴OB=1.4m.
∴乒乓球第一次落地点B距斜坡底端O的距离为1.4m.
故答案为:1.4.
(2)由题意,∵乒乓球第二次弹起运行路线的抛物线与第一次形状相同,且最大高度为1.21m,
∴设乒乓球第二次弹起运行路线的抛物线为y2=﹣(x﹣h)2+1.21,
将(1.4,0)代入解析式得:0=﹣(1.4﹣h)2+1.21,
解得 h1=2.5,h2=0.3 (舍),
∴乒乓球第二次弹起运行路线的抛物线为y2=﹣(x﹣2.5)2+1.21.
当y2=0时,则﹣(x﹣2.5)2+1.21=0,
解得x1=3.6,x2=1.4(舍);
当y2=0.4时,则﹣(x﹣2.5)2+1.21=0.4,
解得x1=3.4,x=1.6(舍).
∴当3.4≤OC≤3.6m时,小强确保获胜.
∴小强将木板立在到斜坡底端O的最小距离3.4m.
故答案为:3.4.
【点评】本题主要考查二次函数的应用,关键是求出乒乓球第一次、第二次弹起运行路线的抛物线解析式.
三.解答题(共8小题)
17.【答案】该男生在此项考试中能得满分.
【分析】根据题意设出y关于x的函数表达式,再用待定系数法求函数解析式即可;然后根据该同学此次投掷实心球的成绩就是实心球落地时的水平距离,令y=0,解方程即可.
【解答】解:该男生在此项考试中能得满分,理由:
根据题意设y关于x的函数表达式为y=a(x﹣5)2+4.8,
把(0,1.8)代入解析式得:1.8=a(0﹣5)2+4.8,
解得:a,
∴y关于x的函数表达式为y=﹣,(x﹣5)2+4.8,
令y=0,则(x﹣5)2+4.8=0,
解得:x1=5+2,x2=5﹣2(舍去),
∵5+210,
∴该男生在此项考试中能得满分.
【点评】本题考查二次函数的应用和一元二次方程的解法,关键是理解题意把函数问题转化为方程为题.
18.【答案】(1);
(2);
(3)点P的横坐标是.
【分析】(1)先求出点A(﹣3,0),C(0,4),再利用待定系数法求出抛物线的解析式即可;
(2)先求出,过点P作PK⊥y轴于点K,再求出,即可求出答案;
(3)过点D作DM⊥AC交CA延长线于点M,DN⊥CE于点N,证明△DMA≌△DNE(AAS),得到DM=DN,再求出F(3,0),待定系数法求出直线CF的解析式为.联立与求出点,设点D(0,m),过点E作EQ⊥OD于点Q,则,根据AD2=OA2+OD2,DE2=EQ2+DQ2求得,则,由 求出t的值,即可得到答案.
【解答】解:(1)∵直线y=﹣x+4经过A,C两点,
∴当x=0时,y=4;当y=0时,x=﹣3,
∴点A、点C的坐标为:A(﹣3,0),C(0,4),
抛物线y=ax2﹣ax+c与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,把A(﹣3,0),C(0,4)代入y=ax2﹣ax+c得:
,
解得,
∴抛物线的解析式为;
(2)∵OC=4,OA=3,
∴AC=5,
∴,
过点P作PK⊥y轴于点K,如图2,
∴PK=t,
∵PD∥AC,
∴∠CDP=∠ACO,
∴,
∴;
(3)过点D作DM⊥AC交CA延长线于点M,DN⊥CE于点N,如图3,
∴∠DMA=DNE=90°,
∵四边形ADEC的内角和为(4﹣2)×180°=360°,∠ACE+∠ADE=180°,
∴∠CAD+∠CED=180°,
∵∠CAD+∠MAD=180°,
∴∠CED=∠MAD,
∵AD=DE,
∴△DMA≌△DNE(AAS),
∴DM=DN,
∴CD平分∠ACF,
∵CO⊥AF,
∴CA=CF,
∴OF=OA=3,
∴F(3,0),
设直线CF的解析式为y=kx+b,
∴,
解得,
∴直线CF的解析式为.
联立与组成方程组得:
,
解得x1=0,x2=5,
∴,
设点D(0,m),过点E作EQ⊥OD于点Q,
∴,
∴AD2=OA2+OD2,DE2=EQ2+DQ2,
∴,
解得,
∴,
∴,
解得,
∴点P的横坐标是.
【点评】此题是二次函数综合题,考查了待定系数法、一次函数的图象和性质、解直角三角形、勾股定理、全等三角形的判定和性质等知识,数形结合和正确添加辅助线是解题的关键.
19.【答案】(1)该种水果的售价应定为11元;
(2)若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为12元.
【分析】(1)设该种水果的售价为x元/kg,则每千克的利润为(x﹣8)元,每天可售出(320﹣20x)kg,利用总利润=每千克的利润×日销售量,即可得出关于x的一元二次方程,解之即可得出结论;
(2)设销售该种水果的利润为w元,根据总利润=每千克的利润×日销售量列出函数解析式,再由函数的性质求出最值.
【解答】解:(1)设该种水果的售价应定为x元,则每千克的利润为(x﹣8)元,每天可售出40+20(14﹣x)=(320﹣20x)千克,
根据题意得:(x﹣8)(320﹣20x)=300,
整理得:x2﹣24x+143=0,
解得:x1=11,x2=13,
因为优惠顾客,所以取 x=11,
答:该种水果的售价应定为11元;
(2)设销售该种水果的利润为w元,
根据题意得:w=(x﹣8)(320﹣20x)=﹣20(x﹣12)2+320,
∵﹣20<0,
∴当x=12时,w有最大值,最大值为320,
∴若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为12元.
【点评】本题考查了二次函数和一元二次方程的应用,找准等量关系,正确列出二次函数解析式和一元二次方程是解题的关键.
20.【答案】(1)y与x之间的函数关系式为y=﹣5x+200;
(2)当x=31时,w有最大值,最大值为405元.
【分析】(1)根据题目条件设出一次函数关系式,将点的坐标代入即可;
(2)设超市每天销售意米的利润为w(元),根据“利润=销售量×每千克利润”列出函数关系式,再根据二次函数的性质解答即可.
【解答】(1)设y与x之间的函数关系式为y=kx+b(k≠0),
根据表格可知函数经过点(26,70),(28,60),
根据题意得:,
解得:,
∴y与x之间的函数关系式为y=﹣5x+200;
(2)设超市每天销售意米的利润为w(元),
根据题意得:w=(﹣5x+200)(x﹣22),
=﹣5x2+310x﹣4400,
=﹣5(x﹣31)2+405,
又∵x≤34,
∴当x=31时,w有最大值,最大值为405元.
【点评】本题主要考查了二次函数的应用,读懂题意并熟练地列出函数关系式是解答本题的关键.
21.【答案】见试题解答内容
【分析】分析:(1)由x=0与x=3时的函数值相等,列方程求出t值即可求解;
(2)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点D,用未知数设出点P、D的坐标,即可得到线段PD的长度表达式,以PD为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标;
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,求出直线AH的解析式,利用方程组即可即可求出点P坐标;
【解答】解:(1)∵x=0与x=3时的函数值相等,
∴(t﹣1)×02+(t+1)×0+2=(t﹣1)×32+(t+1)×3+2,
解方程,得t,
把t代入二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),
∴二次函数的解析式为:y.
(2)如图过点P作PD∥y轴,交BC于点D.
把y=0代入y,得为:0,
解,得x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0),
又∵C(0,2)
∴直线BC:yx+2,
设点P(a,),
把x=a代入yx+2,ya+2,
∴点D的坐标为(a,a+2),
∴PD(a+2),
∴S△PBC()×4=﹣a2+4a=﹣(a﹣2)2+4,
当a=2时,S△PBC有最大值,最大值为4,
所以点P的坐标(2,3),
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,
∵A(﹣1,0),H(,),
∴直线AH的解析式为yx,
由,解得或,
∴P(,).
【点评】此题考查的内容在二次函数综合题中较为常见,主要涉及了:一次(二次)函数解析式的确定、三角形面积的解法、二次函数的应用等基础知识.
22.【答案】(1)抛物线为yx2+4,球不能否射进球门;(2)小王应该带球向正后方移动1米射门.
【分析】(1)依据题意,顶点为(0,4),从而可设抛物线为y=ax2+4,又抛物线过A(6,0),故可得解析式,再结合B点横坐标代入解析式求出此时球的高度与球门比较可以得解;
(2)依据题意,由于射门路线的形状、最大高度均保持不变,从而可设此时的抛物线为y(x﹣m)2+4(m>0),又抛物线过点(﹣3,),可得m,从而得此时解析式,再令y=0,求出此时踢球点,最后与A点比较可以得解.
【解答】解:(1)由题意得,顶点为(0,4),
∴可设抛物线为y=ax2+4.
又抛物线过A(6,0),
∴0=36a+4.
∴a.
∴抛物线为yx2+4.
∵B为(﹣3,0),
∴令x=﹣3,故y9+4=3.
∵3>2.44,
∴球不能否射进球门.
(2)由题意,∵射门路线的形状、最大高度均保持不变,
∴可设此时的抛物线为y(x﹣m)2+4(m>0).
又抛物线过点(﹣3,),
∴(﹣3﹣m)2+4.
∴m=﹣7(不合题意,舍去)或m=1.
∴此时抛物线为y(x﹣1)2+4.
令y=0,
∴0(x﹣1)2+4.
∴x=﹣5或x=7.
∴此时踢球点为(7,0).
又A(6,0),
∴小王应该带球向正后方移动1米射门.
【点评】本题主要考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
23.【答案】(1)yx2+2x+3;(2)不能正常通过;(3)钢架BAC的最大长度为9m.
【分析】(1)依据题意,设抛物线的解析式为y=ax2+bx+c,将已知点的坐标代入求出a,b,c后即可得解;
(2)依据题意,由工程车高5m,从而令y=5,即5x2+2x+3,求出x的值,进而得出能通过的工程车宽度与已知工程车车款4m进行比较即可得解;
(3)依据题意,结合图象,设A(m,m2+2m+3),再由B在墙面上,得出m的范围,又由AB+AC=mm2+2m+3(m)2,进而由二次函数的性质可以判断得解.
【解答】解:(1)由题意,设抛物线的解析式为y=ax2+bx+c,
∴.
∴.
∴抛物线的解析式为yx2+2x+3.
(2)工程车不能正常通过.理由如下:
∵工程车高5m,
∴令y=5,即5x2+2x+3.
∴x=3±.
∴纵坐标为5时,两点的距离为3(3)=23.46<4.
故高5m,顶部宽4m的工程车不能正常通过.
(3)由题意,如图,
设A(m,m2+2m+3).
当OB=3时,令y=3m2+2m+3,
∴m=0或m=6.
∴B(0,m2+2m+3).
∵B在墙面上,
∴m≥6.
由AB+AC=mm2+2m+3
m2+3m+3
(m)2,
又当m时,(AB+AC)的值随m的增大而减小,
∴当m=6时,(AB+AC)取最大值,最大值为9.
∴钢架BAC的最大长度为9m.
【点评】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用是关键.
24.【答案】(1)y(x﹣2)2+3;(2)球不能射进球门;(3)1≤n≤4.
【分析】(1)用待定系数法即可求解;
(2)当x=0时,y4+32.44,即可求解;
(3)移动后的抛物线为y(x﹣2﹣n)2+3,把点(0,2.25)代入上式求出n,同理把(0,0)代入函数表达式求出n,进而求解.
【解答】解:(1)∵8﹣6=2,
∴抛物线的顶点坐标为(2,3),设抛物线 y=a(x﹣2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a,
∴抛物线的函数表达式为y(x﹣2)2+3;
(2)当x=0时,
y4+32.44,
∴球不能射进球门;
(3)设小明带球向正后方移动n米,则移动后的抛物线为y(x﹣2﹣n)2+3,
把点(0,2.25)代入得:2.25(0﹣2﹣n)2+3,
解得 n=﹣5(舍去)或n=1,
把点(0,0)代入得:0(0﹣2﹣n)2+3,
解得:n=﹣8(舍去)或n=4,
即1≤n≤4.
【点评】本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.4 二次函数的应用
一.选择题(共10小题)
1.如图,要修建一个圆形喷水池,在池中心O点竖直安装一根水管,在水管的顶端A处安一个喷水头,使喷出的抛物线形水柱在与池中心O点的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心O点3m.则水管OA的高是( )
A.2m B.2.25m C.2.5m D.2.8m
2.把一个足球垂直于水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤3).若存在两个不同的t的值,使足球离地面的高度均为a米,则a的取值范围是( )
A.0≤a≤15 B.0≤a<20 C.15≤a<20 D.15≤a≤20
3.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段OA表示水平的路面,以O为坐标原点OA所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量OA=12m,抛物线的顶点P到OA的距离为5m,则抛物线的函数表达式为( )
A. B.
C. D.
4.在一个边长为5的正方形中挖去一个边长为x(0<x<5)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )
A.y=x2 B.y=25﹣x2 C.y=x2﹣25 D.y=25﹣2x
5.将进货单价为90元的某种商品按100元售出时,能卖出500个,单价每上涨1元,其销售量就减小10个,为了获得最大利润,售价应定为每件( )
A.110元 B.120元 C.130元 D.150元
6.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件,要使利润最大,每件的售价应为( )
A.24元 B.25元 C.28元 D.30元
7.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:①AB=30m;②池底所在抛物线的解析式为;③若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离变为1.2m;④池塘最深处到水面CD的距离为3.2m;其中结论错误的是( )
A.① B.② C.③ D.④
8.用40cm的绳子围成一个矩形,则矩形面积ycm2与一边长为xcm之间的函数关系式为( )
A.y=x2 B.y=﹣x2+40x C.y=﹣x2+20x D.y=﹣x2+20
9.已知多项式A=x2﹣3x+1+n,B=ax2+2x+b(a≠0).
①当n=0时,若A=0,则;
②当n=0,b=0时,若对任意的实数x都有A+B≥0,则a的取值范围为a>﹣1;
③当,a=1,b=6时,的最小值为.
以上说法正确的个数是( )
A.0 B.1 C.2 D.3
10.如图,一段抛物线y=﹣x2+6x(0≤x≤6),记为抛物线C1,它与x轴交于点O、A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3,…如此进行下去,得到一条“波浪线”,若点M(2021,m)在此“波浪线”上,则m的值为( )
A.﹣5 B.5 C.﹣8 D.8
二.填空题(共6小题)
11.从地面竖直向上抛出一小球,小球离地面的高度h(米)与小球运动时间t(秒)之间关系是h=30t﹣5t2(0≤t≤6),则小球从抛出后运动5秒共运动的路径长是 米.
12.如图,是一名排球运动员发球时,排球行进过程中形成的抛物线,按照图中所示的平面直角坐标系,排球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是,球场的边界距O点的水平距离为18米,则此排球是否会出界? (填“是”或“否”).
13.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为yx2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.
14.对于向上抛的物体,在没有空气阻力的条件下,上升高度h,初速度v,抛出后所经历的时间t,这三个量之间有如下关系:h=vtgt2(其中g是重力加速度,g取10m/s2).将一物体以v=21m/s的初速度向上抛,当物体处在离抛出点18m高的地方时,t的值为 .
15.北京冬奥会推出的吉祥物“冰墩墩”“雪容融”深受人们的喜爱,销售火爆.某经销商以60元/个的价格购进了一批“冰墩墩”摆件,打算采取线下和线上两种方式销售,调查发现线下每周销售量y(个)与售价x(元/个)(x>60)满足一次函数关系:
售价x(元/个) … 80 90 100 …
销量y(个) … 400 300 200 …
线下销售,每个摆件的利润不得高于进价的80%;线上售价为100元/个,供不应求.若该经销商共购进“冰墩墩”1000个,一周内全部销售完.合理分配线下和线上的销量,可使全部售完后获得的利润最大,最大利润是 元(不计其它成本).
16.小明和小强做弹球游戏,如图1,小明向斜坡找一个乒乓球,乒乓球弹起的运行路线是一条抛物线,乒乓球落地后又弹起,第二次弹起的运行路线和第一次运行路线的抛物线形状相同.小强在地面立一块高度为0.4m的木板,以斜坡底端O为坐标原点,地面水平线为x轴,取单位长度为1m,建立如图2所示的平面直角坐标系,乒乓球的大小忽略不计,经测量发现,抛球点A的坐标为(﹣1,3.36),第一次弹起的运行路线最高点坐标为(﹣0.5,3.61),第二次弹起的最大高度为1.21m.
(1)求乒乓球第一次落地点B距斜坡低端O的距离是 m;
(2)为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端O的最小距离是 m.
三.解答题(共8小题)
17.如图所示,一名男生掷出的实心球行进高度y(m)与水平距离x(m)之间的函数图象是一条抛物线,掷出时起点处高度为1.8m,当水平距离为5m时,实心球行进至最高点4.8m处.若实心球从起点到落地点的水平距离不小于10m时可得满分,问该男生此次抛掷能否得到满分?请说明理由.
18.如图1,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣ax+c与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,直线经过A,C两点.
(1)求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,PD∥AC交y轴于点D,若设线段PD的长为d,点P的横坐标为t,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,连接AD,点E为抛物线上第四象限上一点,AD=AE,连接CE交x轴于点F,若∠ACE+∠ADE=180°,求点P的横坐标.
19.某水果店以8元/kg的价钱购进了一批水果,已知当售价为14元/kg时,每天可卖出40kg,为了扩大销售,增加盈利,同时优惠顾客,该水果店决定对该种水果降价销售.经调查发现,售价每千克降低1元时,则可多售出20kg.
(1)若要该水果店每天销售该种水果的利润达到300元,则该种水果的售价应定为多少元?
(2)若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为多少元?
20.金沙意米是仙游县著名的土特产、它品质优异,荣获国家地理标志证明商标,某超市销售的金沙意米,成本价为每千克22元,超市限定售价不高于每千克34元.销售中平均每天销售量y(kg)与销售单价x(元)的关系可以近似地看作一次函数,如表所示:
x 26 28 30 32
y 70 60 50 40
(1)求出y与x之间的函数关系式;
(2)设超市每天销售意米的利润为w(元),求w与x之间的函数关系式,当x取何值时,w的值达到最大?最大值是多少?
21.如图,二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
(1)求二次函数的解析式.
(2)在第一象限的抛物线上求点P,使得S△PBC最大.
(3)点P是抛物线上x轴上方一点,若∠CAP=45°,求P点坐标.
22.足球作为一项重要的体育运动,越来越受到广大体育爱好者的喜欢,校园足球更是同学们的最爱.在一次足球训练中,小王从球门正前方9米的A处射门,球射向球门的路线呈抛物线形.当球飞行的水平距离为6米时,球达到最高点D,此时球离地面4米.已知球门BC的高为2.44米,现以O为原点建立如图所示的平面直角坐标系.
(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,请通过计算说明当时小王应该带球向正后方移动多少米射门,才能让足球经过B点正上方米处入门?
23.某一抛物线形隧道,一侧建有垂直于地面的隔离墙,其横截面如图所示,并建立平面直角坐标系.已知抛物线经过(0,3),,三点.
(1)求抛物线的解析式(不考虑自变量的取值范围);
(2)有一辆高5m,顶部宽4m的工程车要通过该隧道,该车能否正常通过?并说明理由;
(3)现准备在隧道上A处安装一个直角形钢架BAC,对隧道进行维修.B,C两点分别在隔离墙和地面上,且AB与隔离墙垂直,AC与地面垂直,求钢架BAC的最大长度.
24.足球训练中球员从球门正前方8米的A处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米.现以O为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式;
(2)已知球门高OB为2.44米,通过计算判断球能否射进球门(忽略其他因素);
(3)已知点C为OB上一点,OC=2.25米,若射门路线的形状、最大高度均保持不变,当时球员带球向正后方移动n米再射门,足球恰好经过OC区域(含点O和C),求n的取值范围.
2.4 二次函数的应用
参考答案与试题解析
一.选择题(共10小题)
1.【答案】B
【分析】利用顶点式求得抛物线的解析式,再令x=0,求得相应的函数值,即为所求的答案.
【解答】解:由题意可知点(1,3)是抛物线的顶点,
∴设这段抛物线的解析式为y=a(x﹣1)2+3.
∵该抛物线过点(3,0),
∴0=a(3﹣1)2+3,
解得:a.
∴y(x﹣1)2+3.
∵当x=0时,y(0﹣1)2+332.25,
∴水管应长2.25m.
故选:B.
【点评】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握待定系数法及二次函数的相关性质是解题的关键.
2.【答案】C
【分析】由题意可得方程a=20t﹣5t2,存在两个不同的t的值,使足球离地面的高度均为a,故Δ=b2﹣4ac>0,即可求出相应的范围.
【解答】解:由题意得方程a=20t﹣5t2,有两个不相等的实根
∴Δ=b2﹣4ac>0,即202﹣4×5a>0
∴0≤a<20
又∵0≤t≤3
∴当t=3时,a=20×3﹣5×32=60﹣45=15,
所以a的取值范围为:15≤a<20,
故选:C.
【点评】本题主要考查二次函数的应用,解题的关键是根据题意得到相应的方程及将实际问题转化为方程问题.
3.【答案】D
【分析】由OA的长度及点P到OA的距离,可得出点P的坐标,设出抛物线的顶点式,利用待定系数法,即可求出抛物线的函数表达式.
【解答】解:∵OA=12m,抛物线的顶点P到OA的距离为5m,
∴抛物线顶点P的坐标为(6,5),
设抛物线的函数表达式为y=a(x﹣6)2+5,
将O(0,0)代入y=a(x﹣6)2+5得:0=36a+5,
解得:a,
∴抛物线的函数表达式为y(x﹣6)2+5,
故选:D.
【点评】本题考查了待定系数法求二次函数解析式,根据给定点的坐标,利用待定系数法求出二次函数解析式是解题的关键.
4.【答案】B
【分析】利用剩余部分的面积=大正方形的面积﹣小正方形的面积,即可找出y关于x的函数解析式.
【解答】解:根据题意得:y=52﹣x2,
∴y关于x的函数解析式是y=25﹣x2.
故选:B.
【点评】本题考查了根据实际问题列二次函数关系式,根据各数量之间的关系,找出y关于x的函数解析式是解题的关键.
5.【答案】B
【分析】设售价上涨x元,利润y元,根据将进货价为90元的某种商品按100元出售时,能卖出500个,商品每个上涨1元,其销售量就减少10个,则售价为(100+x)元,销售量为(500﹣10x)个,可列出二次函数解析式,把二次函数解析式化为顶点式即可求得结果.
【解答】解:设在售价100元的基础上涨价x元,获总利润y元,
则y=(100+x﹣90)(500﹣10x)=﹣10(x﹣20)2+9000,
所以x=20时,y值最大,
所以售价应定为120元,
故选:B.
【点评】本题主要考查了二次函数的应用,能够求出二次函数解析式是解决问题的关键.
6.【答案】B
【分析】设利润为w根据利润等于利润单价乘以数量列出函数,根据函数性质求解即可得到答案.
【解答】解:设利润为w 元,
由题意可得,w=(x﹣20)(30﹣x)=﹣x2+50x﹣600=﹣(x﹣25)2+25,
∵﹣1<0,20≤x≤30,
∴当x=25时w最大,
故选:B.
【点评】本题考查二次函数解决销售利润问题中最值问题,解题的关键是列出函数根据函数性质求解.
7.【答案】C
【分析】根据图象可以判断①;设出池底所在抛物线的解析式为y=ax2﹣5,再把(15,0)代入解析式求出a即可判断②;把x=12代入解析式求出y=﹣1.8,再用5﹣1.8即可判断③;把x=6代入解析式即可判断④.
【解答】解:①观察图形可知,AB=30m,
故①正确;
②设池底所在抛物线的解析式为y=ax2﹣5,
将(15,0)代入,可得a,
故抛物线的解析式为yx2﹣5;
故②正确;
③当池塘中水面的宽度减少为原来的一半,即水面宽度为12m时,
将x=6代入yx2﹣5,得y=﹣4.2,
可知此时最深处到水面的距离为5﹣4.2=0.8(m),
即为原来的,
故③错误;
④∵yx2﹣5,
∴当x=12时,y=﹣1.8,
故池塘最深处到水面CD的距离为5﹣1.8=3.2(m),
故④正确.
故选:C.
【点评】本题考查了二次函数的应用,体现了数学建模、数学抽象、数学运算素养.
8.【答案】C
【分析】先根据矩形一边长为xcm,周长为40cm得出另一边长为20﹣x(cm),再根据矩形的面积公式可得答案.
【解答】解:∵矩形一边长为xcm,周长为40cm,
∴另一边长为20﹣x(cm),
∴矩形的面积y=x(20﹣x)=﹣x2+20x,
故选:C.
【点评】本题主要考查根据实际问题列出二次函数关系式,根据实际问题确定二次函数关系式关键是读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数图象要根据自变量的取值范围来确定.
9.【答案】B
【分析】由当n=0时,A=0,得x2﹣3x+1=0,可得x3,故(x)2=9,从而x27,判断①错误;当n=0,b=0时,对任意的实数x都有A+B≥0,可知(a+1)x2﹣x+1≥0对任意x均成立;即抛物线y=(a+1)x2﹣x+1在x轴上或x轴的上方;故,可得得a,判断②错误;当,a=1,b=6时,,可看作x轴上的点(x,0)到点(,)及点(﹣1,)的距离之和,即可知当点(x,0),点(,)及点(﹣1,)共线时,取最小值,的最小值为,判断③正确.
【解答】解:根据题意得:x2﹣3x+1=0,此时x≠0,
∴x2+1=3x可得x3,
∴(x)2=9,
∴x27,故①错误;
∵当n=0,b=0时,对任意的实数x都有A+B≥0,
∴x2﹣3x+1+ax2+2x≥0,
即(a+1)x2﹣x+1≥0对任意x均成立;
∴抛物线y=(a+1)x2﹣x+1在x轴上或x轴的上方;
∴a+1>0且Δ<0,
∴,
解得a,故②错误;
当,a=1,b=6时,A=x2﹣3x,B=x2+2x+6,
∴
,
而可看作x轴上的点(x,0)到点(,)及点(﹣1,)的距离之和,
∴当点(x,0),点(,)及点(﹣1,)共线时,取最小值,最小值即为点(,)和点(﹣1,)之间的距离,
∴的最小值为,故③正确;
∴正确的有③,共1个;
故选:B.
【点评】本题考查二次函数的应用,两点间的距离公式的应用,完全平方公式的应用等知识,解题的关键是灵活掌握二次函数与二次不等式的关系及两点间的距离公式.
10.【答案】B
【分析】根据y=﹣x2+6x(0≤x≤6)可以得到:整个函数图象每隔6×2=12个单位长度,函数值就相等,而2021=12×168+5,由此即可计算.
【解答】解:∵y=﹣x2+6x=﹣x(x﹣6)(0≤x≤6),
∴A1(6,0),
∴整个函数图象每隔6×2=12个单位长度,函数值就相等,
∵2021=12×168+5,
所以m的值等于x=5时的纵坐标,
所以m=﹣52+6×5=5.
故选:B.
【点评】本题考查了抛物线与x轴的交点,二次函数的性质,二次函数与几何变换,解决此题的关键在于能根据函数图象发现规律:m的值等于x=5时的纵坐标.
二.填空题(共6小题)
11.【答案】65.
【分析】根据题目中的函数解析式可以求得h的最大值,从而可以求得小球从抛出后运动5秒共运动的路径长,本题得以解决.
【解答】解:∵h=30t﹣5t2=﹣5(t﹣3)2+45(0≤t≤6),
当t=3时,h取得最大值,此时h=45,
当t=5时,h=25,
∴小球从抛出后运动5秒共运动的路径长是:45+(45﹣25)=65(米),
故答案为:65.
【点评】本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的总的路径的长.
12.【答案】见试题解答内容
【分析】令y=0,解方程求出相应的x的值,与18比较即可.
【解答】解:令y=0,则(x﹣6)2+2.8=0,
解得x1=6+2,x2=6﹣2(舍去),
∵6+218,
∴此排球是会出界,
故答案为:是.
【点评】本题考查二次函数的应用,解答本题的关键是求出抛物线与x轴正半轴的交点的横坐标的值.
13.【答案】见试题解答内容
【分析】令y=8,即yx2+10=8,求出x值,进而求解.
【解答】解:令y=8,即yx2+10=8,
解得:x=±4,
∴则EF=4(﹣4)=8(米).
【点评】本题考查的是二次函数在实际生活中的应用,解题的关键是弄懂题意,该题比较简单.
14.【答案】或3.
【分析】把v=21,h=18代入h=vtgt2得一元二次方程,求解即可.
【解答】解:把v=21,h=18代入h=vtgt2得,
18=21t10t2,
整理得:5t2﹣21t+18=0,
解得t1,t2=3,
∴当物体处在离抛出点18m高的地方时,t的值为或3.
故答案为:或3.
【点评】此题主要考查了二次函数的应用以及一元二次方程的解法,正确把已知数据代入是解题关键.
15.【答案】40960.
【分析】根据总利润=线下销售利润+线上销售利润列出函数解析式找最值.
【解答】解:设y与x的函数表达式为y=kx+b,代入得:
,
解得:,
∴y与x的函数表达式为 y=﹣10x+1200,
当线下销量为(﹣10x+1200))个时,线上销量为1000﹣(﹣10x+1200)=(10x﹣200)个,
设全部售完后获得的利润为w元,根据题意得:
w=(x﹣60)(﹣10x+1200)+(100﹣60)(10x﹣200)
=﹣10x2+2200x﹣80000
=﹣10(x﹣110)2+41000,
∵线下销售,每个摆件的利润不得高于进价的80%,
∴x﹣60≤60×80,
解得:x≤108,
∵﹣10<0,对称轴为x=110,
∴当x=108时,w有最大值,最大值为40960元,
故答案为:40960.
【点评】本题考查了二次函数的应用和待定系数法求函数解析式,关键是设出y与x的函数表达式为y=kx+b,然后用待定系数法求函数解析式即可.
16.【答案】(1)1.4;(2)3.4.
【分析】(1)依据题意,根据已知条件设出抛物线的顶点式解析式,再把A点坐标代入解析式求出a即可得出解析式,然后令y=0,解方程求出x即可;
(2)依据题意,用待定系数法求出乒乓球第二次弹起运行路线的抛物线解析式,再令y=0和y=0.4,进而可以判断得解.
【解答】解:(1)由题意得,乒乓球第一次弹起运行路线的抛物线顶点为 (﹣0.5,3.61),过点A(﹣1,3.36),
设乒乓球第一次弹起运行路线的抛物线解析式为y1=a(x+0.5)2+3.61,
代入A(﹣1,3.36)得:3.36=a(﹣1+0.5)2+3.61,
解得 a=﹣1,
∴乒乓球第一次弹起运行路线的抛物线解析式为y1=﹣(x+0.5)2+3.61=﹣x2﹣x+3.36.
令 y1=0,
∴﹣(x+0.5)2+3.61=0.
∴解得 x1=1.4,x2=﹣2.4 (舍).
∴OB=1.4m.
∴乒乓球第一次落地点B距斜坡底端O的距离为1.4m.
故答案为:1.4.
(2)由题意,∵乒乓球第二次弹起运行路线的抛物线与第一次形状相同,且最大高度为1.21m,
∴设乒乓球第二次弹起运行路线的抛物线为y2=﹣(x﹣h)2+1.21,
将(1.4,0)代入解析式得:0=﹣(1.4﹣h)2+1.21,
解得 h1=2.5,h2=0.3 (舍),
∴乒乓球第二次弹起运行路线的抛物线为y2=﹣(x﹣2.5)2+1.21.
当y2=0时,则﹣(x﹣2.5)2+1.21=0,
解得x1=3.6,x2=1.4(舍);
当y2=0.4时,则﹣(x﹣2.5)2+1.21=0.4,
解得x1=3.4,x=1.6(舍).
∴当3.4≤OC≤3.6m时,小强确保获胜.
∴小强将木板立在到斜坡底端O的最小距离3.4m.
故答案为:3.4.
【点评】本题主要考查二次函数的应用,关键是求出乒乓球第一次、第二次弹起运行路线的抛物线解析式.
三.解答题(共8小题)
17.【答案】该男生在此项考试中能得满分.
【分析】根据题意设出y关于x的函数表达式,再用待定系数法求函数解析式即可;然后根据该同学此次投掷实心球的成绩就是实心球落地时的水平距离,令y=0,解方程即可.
【解答】解:该男生在此项考试中能得满分,理由:
根据题意设y关于x的函数表达式为y=a(x﹣5)2+4.8,
把(0,1.8)代入解析式得:1.8=a(0﹣5)2+4.8,
解得:a,
∴y关于x的函数表达式为y=﹣,(x﹣5)2+4.8,
令y=0,则(x﹣5)2+4.8=0,
解得:x1=5+2,x2=5﹣2(舍去),
∵5+210,
∴该男生在此项考试中能得满分.
【点评】本题考查二次函数的应用和一元二次方程的解法,关键是理解题意把函数问题转化为方程为题.
18.【答案】(1);
(2);
(3)点P的横坐标是.
【分析】(1)先求出点A(﹣3,0),C(0,4),再利用待定系数法求出抛物线的解析式即可;
(2)先求出,过点P作PK⊥y轴于点K,再求出,即可求出答案;
(3)过点D作DM⊥AC交CA延长线于点M,DN⊥CE于点N,证明△DMA≌△DNE(AAS),得到DM=DN,再求出F(3,0),待定系数法求出直线CF的解析式为.联立与求出点,设点D(0,m),过点E作EQ⊥OD于点Q,则,根据AD2=OA2+OD2,DE2=EQ2+DQ2求得,则,由 求出t的值,即可得到答案.
【解答】解:(1)∵直线y=﹣x+4经过A,C两点,
∴当x=0时,y=4;当y=0时,x=﹣3,
∴点A、点C的坐标为:A(﹣3,0),C(0,4),
抛物线y=ax2﹣ax+c与x轴负半轴交于点A,与x轴正半轴于点B,交y轴于点C,把A(﹣3,0),C(0,4)代入y=ax2﹣ax+c得:
,
解得,
∴抛物线的解析式为;
(2)∵OC=4,OA=3,
∴AC=5,
∴,
过点P作PK⊥y轴于点K,如图2,
∴PK=t,
∵PD∥AC,
∴∠CDP=∠ACO,
∴,
∴;
(3)过点D作DM⊥AC交CA延长线于点M,DN⊥CE于点N,如图3,
∴∠DMA=DNE=90°,
∵四边形ADEC的内角和为(4﹣2)×180°=360°,∠ACE+∠ADE=180°,
∴∠CAD+∠CED=180°,
∵∠CAD+∠MAD=180°,
∴∠CED=∠MAD,
∵AD=DE,
∴△DMA≌△DNE(AAS),
∴DM=DN,
∴CD平分∠ACF,
∵CO⊥AF,
∴CA=CF,
∴OF=OA=3,
∴F(3,0),
设直线CF的解析式为y=kx+b,
∴,
解得,
∴直线CF的解析式为.
联立与组成方程组得:
,
解得x1=0,x2=5,
∴,
设点D(0,m),过点E作EQ⊥OD于点Q,
∴,
∴AD2=OA2+OD2,DE2=EQ2+DQ2,
∴,
解得,
∴,
∴,
解得,
∴点P的横坐标是.
【点评】此题是二次函数综合题,考查了待定系数法、一次函数的图象和性质、解直角三角形、勾股定理、全等三角形的判定和性质等知识,数形结合和正确添加辅助线是解题的关键.
19.【答案】(1)该种水果的售价应定为11元;
(2)若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为12元.
【分析】(1)设该种水果的售价为x元/kg,则每千克的利润为(x﹣8)元,每天可售出(320﹣20x)kg,利用总利润=每千克的利润×日销售量,即可得出关于x的一元二次方程,解之即可得出结论;
(2)设销售该种水果的利润为w元,根据总利润=每千克的利润×日销售量列出函数解析式,再由函数的性质求出最值.
【解答】解:(1)设该种水果的售价应定为x元,则每千克的利润为(x﹣8)元,每天可售出40+20(14﹣x)=(320﹣20x)千克,
根据题意得:(x﹣8)(320﹣20x)=300,
整理得:x2﹣24x+143=0,
解得:x1=11,x2=13,
因为优惠顾客,所以取 x=11,
答:该种水果的售价应定为11元;
(2)设销售该种水果的利润为w元,
根据题意得:w=(x﹣8)(320﹣20x)=﹣20(x﹣12)2+320,
∵﹣20<0,
∴当x=12时,w有最大值,最大值为320,
∴若要该水果店每天销售该种水果的利润达到最大,则该种水果的售价应定为12元.
【点评】本题考查了二次函数和一元二次方程的应用,找准等量关系,正确列出二次函数解析式和一元二次方程是解题的关键.
20.【答案】(1)y与x之间的函数关系式为y=﹣5x+200;
(2)当x=31时,w有最大值,最大值为405元.
【分析】(1)根据题目条件设出一次函数关系式,将点的坐标代入即可;
(2)设超市每天销售意米的利润为w(元),根据“利润=销售量×每千克利润”列出函数关系式,再根据二次函数的性质解答即可.
【解答】(1)设y与x之间的函数关系式为y=kx+b(k≠0),
根据表格可知函数经过点(26,70),(28,60),
根据题意得:,
解得:,
∴y与x之间的函数关系式为y=﹣5x+200;
(2)设超市每天销售意米的利润为w(元),
根据题意得:w=(﹣5x+200)(x﹣22),
=﹣5x2+310x﹣4400,
=﹣5(x﹣31)2+405,
又∵x≤34,
∴当x=31时,w有最大值,最大值为405元.
【点评】本题主要考查了二次函数的应用,读懂题意并熟练地列出函数关系式是解答本题的关键.
21.【答案】见试题解答内容
【分析】分析:(1)由x=0与x=3时的函数值相等,列方程求出t值即可求解;
(2)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点D,用未知数设出点P、D的坐标,即可得到线段PD的长度表达式,以PD为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标;
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,求出直线AH的解析式,利用方程组即可即可求出点P坐标;
【解答】解:(1)∵x=0与x=3时的函数值相等,
∴(t﹣1)×02+(t+1)×0+2=(t﹣1)×32+(t+1)×3+2,
解方程,得t,
把t代入二次函数y=(t﹣1)x2+(t+1)x+2(t≠1),
∴二次函数的解析式为:y.
(2)如图过点P作PD∥y轴,交BC于点D.
把y=0代入y,得为:0,
解,得x1=﹣1,x2=4,
∴点A(﹣1,0),B(4,0),
又∵C(0,2)
∴直线BC:yx+2,
设点P(a,),
把x=a代入yx+2,ya+2,
∴点D的坐标为(a,a+2),
∴PD(a+2),
∴S△PBC()×4=﹣a2+4a=﹣(a﹣2)2+4,
当a=2时,S△PBC有最大值,最大值为4,
所以点P的坐标(2,3),
(3)如图,将AC绕点A顺时针旋转90°得到AC′,则C′(1,﹣1),取CC′的中点H,作直线AH交抛物线于P,则∠CAP=45°,
∵A(﹣1,0),H(,),
∴直线AH的解析式为yx,
由,解得或,
∴P(,).
【点评】此题考查的内容在二次函数综合题中较为常见,主要涉及了:一次(二次)函数解析式的确定、三角形面积的解法、二次函数的应用等基础知识.
22.【答案】(1)抛物线为yx2+4,球不能否射进球门;(2)小王应该带球向正后方移动1米射门.
【分析】(1)依据题意,顶点为(0,4),从而可设抛物线为y=ax2+4,又抛物线过A(6,0),故可得解析式,再结合B点横坐标代入解析式求出此时球的高度与球门比较可以得解;
(2)依据题意,由于射门路线的形状、最大高度均保持不变,从而可设此时的抛物线为y(x﹣m)2+4(m>0),又抛物线过点(﹣3,),可得m,从而得此时解析式,再令y=0,求出此时踢球点,最后与A点比较可以得解.
【解答】解:(1)由题意得,顶点为(0,4),
∴可设抛物线为y=ax2+4.
又抛物线过A(6,0),
∴0=36a+4.
∴a.
∴抛物线为yx2+4.
∵B为(﹣3,0),
∴令x=﹣3,故y9+4=3.
∵3>2.44,
∴球不能否射进球门.
(2)由题意,∵射门路线的形状、最大高度均保持不变,
∴可设此时的抛物线为y(x﹣m)2+4(m>0).
又抛物线过点(﹣3,),
∴(﹣3﹣m)2+4.
∴m=﹣7(不合题意,舍去)或m=1.
∴此时抛物线为y(x﹣1)2+4.
令y=0,
∴0(x﹣1)2+4.
∴x=﹣5或x=7.
∴此时踢球点为(7,0).
又A(6,0),
∴小王应该带球向正后方移动1米射门.
【点评】本题主要考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
23.【答案】(1)yx2+2x+3;(2)不能正常通过;(3)钢架BAC的最大长度为9m.
【分析】(1)依据题意,设抛物线的解析式为y=ax2+bx+c,将已知点的坐标代入求出a,b,c后即可得解;
(2)依据题意,由工程车高5m,从而令y=5,即5x2+2x+3,求出x的值,进而得出能通过的工程车宽度与已知工程车车款4m进行比较即可得解;
(3)依据题意,结合图象,设A(m,m2+2m+3),再由B在墙面上,得出m的范围,又由AB+AC=mm2+2m+3(m)2,进而由二次函数的性质可以判断得解.
【解答】解:(1)由题意,设抛物线的解析式为y=ax2+bx+c,
∴.
∴.
∴抛物线的解析式为yx2+2x+3.
(2)工程车不能正常通过.理由如下:
∵工程车高5m,
∴令y=5,即5x2+2x+3.
∴x=3±.
∴纵坐标为5时,两点的距离为3(3)=23.46<4.
故高5m,顶部宽4m的工程车不能正常通过.
(3)由题意,如图,
设A(m,m2+2m+3).
当OB=3时,令y=3m2+2m+3,
∴m=0或m=6.
∴B(0,m2+2m+3).
∵B在墙面上,
∴m≥6.
由AB+AC=mm2+2m+3
m2+3m+3
(m)2,
又当m时,(AB+AC)的值随m的增大而减小,
∴当m=6时,(AB+AC)取最大值,最大值为9.
∴钢架BAC的最大长度为9m.
【点评】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用是关键.
24.【答案】(1)y(x﹣2)2+3;(2)球不能射进球门;(3)1≤n≤4.
【分析】(1)用待定系数法即可求解;
(2)当x=0时,y4+32.44,即可求解;
(3)移动后的抛物线为y(x﹣2﹣n)2+3,把点(0,2.25)代入上式求出n,同理把(0,0)代入函数表达式求出n,进而求解.
【解答】解:(1)∵8﹣6=2,
∴抛物线的顶点坐标为(2,3),设抛物线 y=a(x﹣2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a,
∴抛物线的函数表达式为y(x﹣2)2+3;
(2)当x=0时,
y4+32.44,
∴球不能射进球门;
(3)设小明带球向正后方移动n米,则移动后的抛物线为y(x﹣2﹣n)2+3,
把点(0,2.25)代入得:2.25(0﹣2﹣n)2+3,
解得 n=﹣5(舍去)或n=1,
把点(0,0)代入得:0(0﹣2﹣n)2+3,
解得:n=﹣8(舍去)或n=4,
即1≤n≤4.
【点评】本题考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
