广东省深圳市南山区2024-2025学年七年级下学期期末数学试题(含答案)
文档属性
| 名称 | 广东省深圳市南山区2024-2025学年七年级下学期期末数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 667.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 00:00:00 | ||
图片预览


文档简介
广东省深圳市南山区2024-2025学年七年级下学期期末数学试题
一、选择题(本题共有8小题,每小题3分,共24分,每小题有4个选项,其中只有一个是正确的)
1.下列四种中国古代青铜器上的纹饰中,是轴对称图形的是( )
A. B.
C. D.
2.下列运算中正确的是( )
A. B.
C. D.
3.如图,小明将一块直角三角板摆放在直尺上,直角顶点落在直尺的边上。若∠1=55°,则∠2的度数为( )
A.255° B.35° C.455° D.555°
4.下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
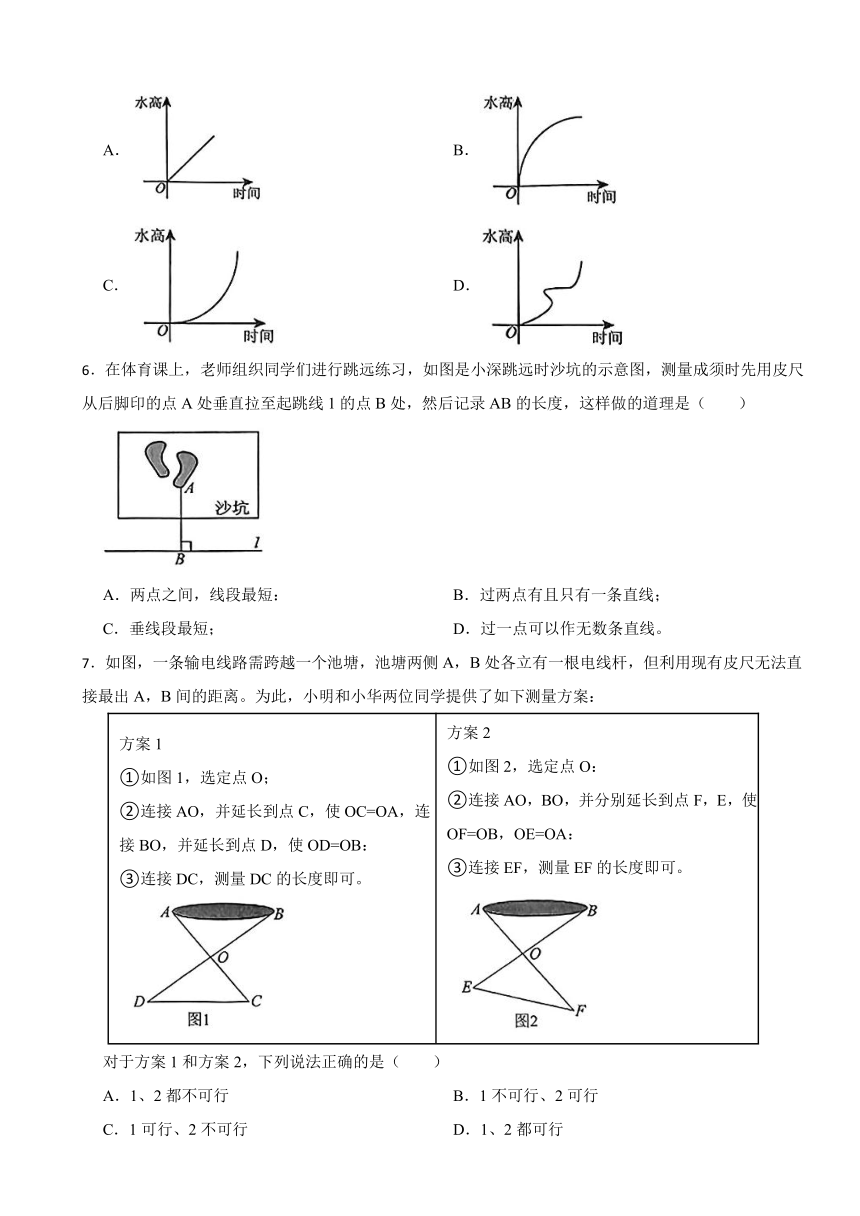
5.茶文化是中国对茶认识的一种具体表现,其内涵与茶具设计之间存在着密不可分的联系。如图,向茶杯中匀速注水,下列哪幅图象能较好刻画出茶杯中水面高度的变化情况( )
A. B.
C. D.
6.在体育课上,老师组织同学们进行跳远练习,如图是小深跳远时沙坑的示意图,测量成须时先用皮尺从后脚印的点A处垂直拉至起跳线1的点B处,然后记录AB的长度,这样做的道理是( )
A.两点之间,线段最短: B.过两点有且只有一条直线;
C.垂线段最短; D.过一点可以作无数条直线。
7.如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接最出A,B间的距离。为此,小明和小华两位同学提供了如下测量方案:
方案1 ①如图1,选定点O; ②连接AO,并延长到点C,使OC=OA,连接BO,并延长到点D,使OD=OB: ③连接DC,测量DC的长度即可。 方案2 ①如图2,选定点O: ②连接AO,BO,并分别延长到点F,E,使OF=OB,OE=OA: ③连接EF,测量EF的长度即可。
对于方案1和方案2,下列说法正确的是( )
A.1、2都不可行 B.1不可行、2可行
C.1可行、2不可行 D.1、2都可行
8.如果将(a+b)n(n为非负整数)的展开式每一项按字母ɑ的次数由大到小排列,就可以得到下面的等式:
观察上述每个式子的各项系数,我们可以得到如右图所示的数表,这就是我国南宋数学家杨辉在其著作《详解九章算法》中提到的数表“杨辉三角”,他揭示了(a+b)n展开后的各项系数的规律。根据这个表,(a+b)7的展开式中所有项系数的和为( )
A.128 B.256 C.512 D.108
二、填空题(每小题3分,共15分,请将正确的答案填在答题卡上)
9.若am=2,a"=8,则am+n= 。
10.一个不透明的袋子里装有红、蓝两种颜色的球共40个,每个球除颜色外都相同,每次摸球前先把球摇匀,从中随机摸出一个球,记下它的颜色后再放回袋子里,不断重复这一过程,将实验后的数据整理成下表:
摸球次数 50 100 200 500 800 1000
摸到红球的频数 11 27 50 124 201 249
摸到红球的频率 0.220 0.270 0.250 0.248 0.251 0.249
请估计袋中红球的个数是 。
11.如图,在Rt△ABC中,∠C=90°,∠B=52°,D、E分别在AB、AC上,将ADE沿DE折叠得到△FDE,且满足EF//AB,则∠EDF= .
12.小南设计了如下的运算程序:任意写下一个三位数(三位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差。重复这个过程,则按照此程序运算2025次后得到的数是 。
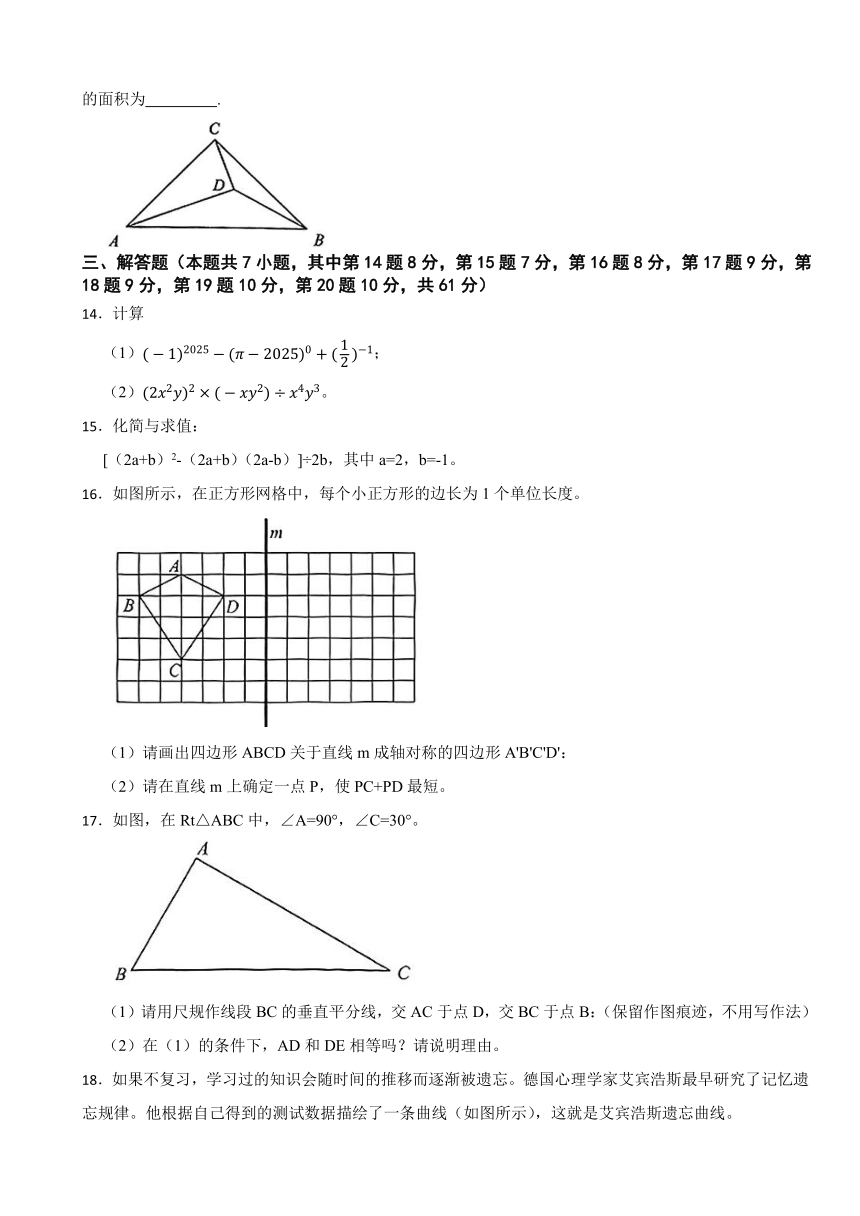
13.如图,在△ABC中,AC⊥BC,AC=BC,点D在△ABC内部,且满足∠ADC=90°,若CD=6,则△BCD的面积为 .
三、解答题(本题共7小题,其中第14题8分,第15题7分,第16题8分,第17题9分,第18题9分,第19题10分,第20题10分,共61分)
14.计算
(1);
(2)。
15.化简与求值:
[(2a+b)2-(2a+b)(2a-b)]÷2b,其中a=2,b=-1。
16.如图所示,在正方形网格中,每个小正方形的边长为1个单位长度。
(1)请画出四边形ABCD关于直线m成轴对称的四边形A'B'C'D':
(2)请在直线m上确定一点P,使PC+PD最短。
17.如图,在Rt△ABC中,∠A=90°,∠C=30°。
(1)请用尺规作线段BC的垂直平分线,交AC于点D,交BC于点B:(保留作图痕迹,不用写作法)
(2)在(1)的条件下,AD和DE相等吗?请说明理由。
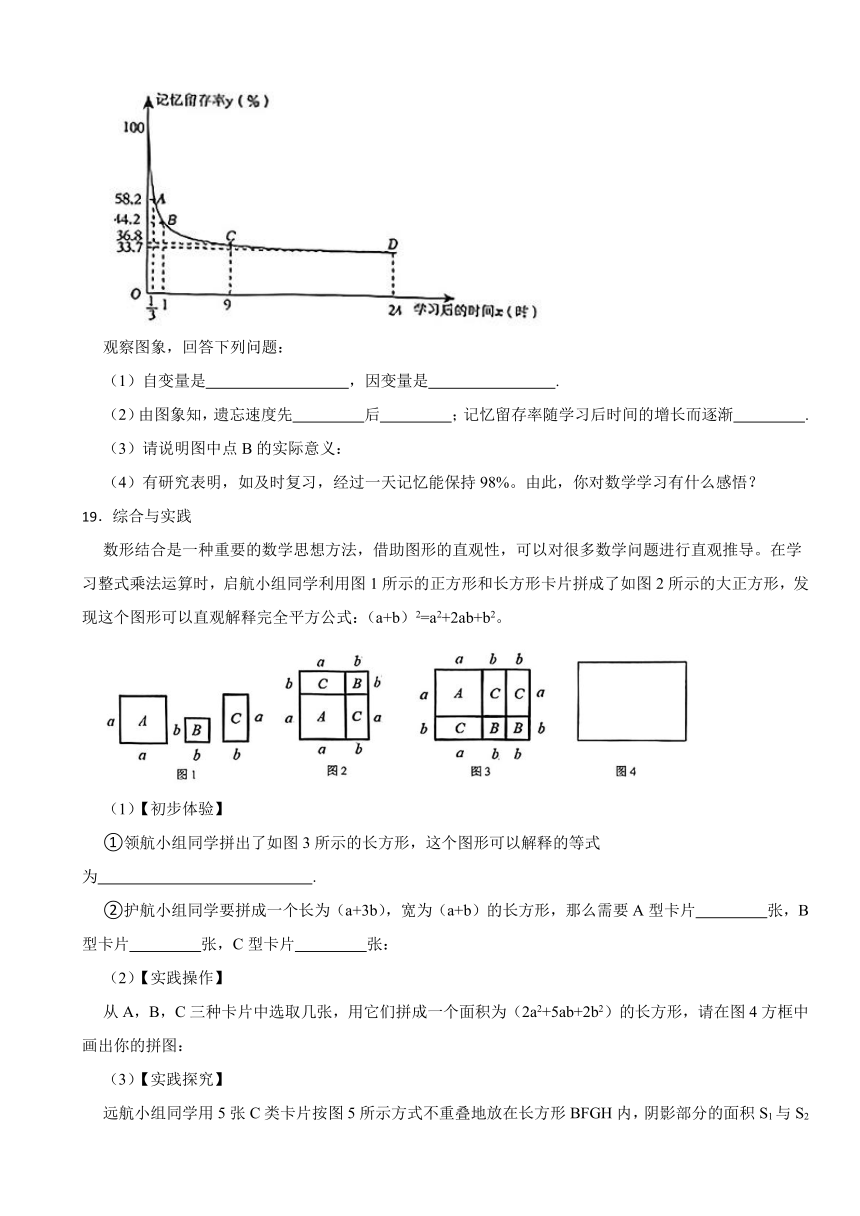
18.如果不复习,学习过的知识会随时间的推移而逐渐被遗忘。德国心理学家艾宾浩斯最早研究了记忆遗忘规律。他根据自己得到的测试数据描绘了一条曲线(如图所示),这就是艾宾浩斯遗忘曲线。
观察图象,回答下列问题:
(1)自变量是 ,因变量是 .
(2)由图象知,遗忘速度先 后 ;记忆留存率随学习后时间的增长而逐渐 .
(3)请说明图中点B的实际意义:
(4)有研究表明,如及时复习,经过一天记忆能保持98%。由此,你对数学学习有什么感悟?
19.综合与实践
数形结合是一种重要的数学思想方法,借助图形的直观性,可以对很多数学问题进行直观推导。在学习整式乘法运算时,启航小组同学利用图1所示的正方形和长方形卡片拼成了如图2所示的大正方形,发现这个图形可以直观解释完全平方公式:(a+b)2=a2+2ab+b2。
(1)【初步体验】
①领航小组同学拼出了如图3所示的长方形,这个图形可以解释的等式为 .
②护航小组同学要拼成一个长为(a+3b),宽为(a+b)的长方形,那么需要A型卡片 张,B型卡片 张,C型卡片 张:
(2)【实践操作】
从A,B,C三种卡片中选取几张,用它们拼成一个面积为(2a2+5ab+2b2)的长方形,请在图4方框中画出你的拼图:
(3)【实践探究】
远航小组同学用5张C类卡片按图5所示方式不重叠地放在长方形BFGH内,阴影部分的面积S1与S2的差与EH的长度无关,设EH的长为x,请探究a与b的数量关系,并说明理由。
20.在面对复杂数学问题时,“特殊化与转化”是重要的问题解决策略。从特殊图形出发,将新研究的问题转化为以前研究过的熟悉的问题,将一般转化为特殊,有助于我们发现解决问题的思路。
【问题背景】
如图1,在等边△ABC中,D、E分别为边BC、AC上任意一点,且BD=CE,连接AD、BE,AD与BE相交于点O。
(1)【特例感知】
当点D为BC中点,点E为AC中点时,请直按写出线段AD与BE的数量关系 ,∠AOE= ;
(2)【一般探究】
当D、E分别为边BC,AC上任意一点时,第一问的结论还成立吗?请说明理由:
(3)【拓展延伸】
如图2,在等边△ABC中,P、M分别为边AB、AC上的点,且AM=BP,过点P作PQ//BE交AC于点Q,交AD于点G;过点M作MN∥AD交BC于点N,交BE于点F,则
①∠MFE= .
②求证:PQ=MN。
答案解析部分
1.解:A、 不是轴对称图形,故A不符合题意;
B、是轴对称图形,故B符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意;
故答案为:B.
2.解:A、,计算错误,故A不符合题意;
B、,计算错误,故B不符合题意;
C、,计算错误,故C不符合题意;
D、 ,计算正确,故D符合题意;
故答案为:D.
3.解:如图,∵∠1=55°,AB//CD,
∴∠3=∠1 =55°,
∴∠2= 180-90-∠3=35°.
故答案为:B.
4.解:A、随机事件是指在一定条件下可能发生也可能不发生的事件,掷3颗骰子,3颗全是6点朝上是可能发生但不必然发生的事件,因此属于随机事件,故A正确;
B、从1,2,3,4,5中随机抽取一个数,偶数为2和4,共2个,概率应为,故B错误;
C、买中国福利彩票中奖是可能发生但非必然发生的事件,属于随机事件,而非必然事件,故C错误
D、拋硬币正面朝上的概率为,连续抛2次的结果可能为(正正)、 (正反)、(反正)、(反反),其中“必有1次正面”不成立(如两次均为反面),故D错误;
故答案为:A.
5.解:∵茶杯下细上粗,
∴水面高度在茶杯中上升的速度先快后慢;
故答案为:B.
6.解:这样做的理由是垂线段最短,
故答案为:C.
7.解:方案1:在△AOB与△COD中,
AO=OC,AOB=COD,OB= OD,
∴△AOB△COD(SAS),
∴AB=CD.
方案2:在△AOB与△EOF中,
AO=EО,
AOB=EOF,
OB=OF
∴△AOB△EOF(SAS),
∴AB=EF.
故答案为:D.
8.解:当n=0时,展开式中所有项的系数和为1,
当n= 1时,展开式中所有项的系数和为2=2' ,
当n=2时,展开式中所有项的系数和为4=22 ,
当n=3时,展开式中所有项的系数和为8=23,
由此可知(a+b)n展开式中所有项的系数和为2n,
则(a+b)7展开式中所有项的系数和是27=128.
故答案为:A.
9.解: ∵ am+n= am an, 且am=2,an=8
∴ am+n=2
故答案为:16.
10.解:观察表格中数据,随着摸球次数增加(500次及以上), 摸到红球的频率稳定在0.25左右,因此可估计摸到红球的概率约为0.25,
设袋中红球个数为x总球数为40得到:,
解得x=10
故答案为:10.
11.解:如图:
∵∠C=90°,∠B=52°,
∴∠A=38°,
∵EF//AB
∴∠BDF=∠A=32°
由折叠的性质得∠EDF=∠ADE,
∴ ∠EDF=71°
故答案为:71°.
12.解:根据题干任意写下一个三位数(三位数字相同的除外)
以三位数321为例:
1.最大数: 321,最小:123 差: 321 - 123= 198,
2.最大数:981,最小数: 189差: 981- 189= 792,
3.最大数: 972,最小数: 279差: 972 - 279=693,
4.最大数: 963, 最小数: 369差:963- 369= 594
5.最大数: 954, 最小数: 459差: 954-459= 495,
6.最大数:954,最小数: 459差: 954-459= 495 ,
开始重复我们发现,从第5步开始,结果稳定在495
故答案为:495.
13.解:如图:过点B作CD延长线的垂线交于点E,
∵BECD, AD⊥DC
∴ADC=BEC
∵AC⊥BC
∴ACD+BCE=90;ACD+CBE=90;
∴ACD=EBC,
∵AC=BC,
∴
∴BE=CD=6,
∴ △BCD的面积.
故答案为:18.
14.(1)解:原式=-1-1+2
=0
(2)解:原式=4x4y2
=-4xy
15.解:原式=(4a2+4ab+b2-4a2+b2)
=(4ab+2b2)
=2a+b
当a=2,b=-1时,
原式==3
16.(1)解:如图:
(2)解:如图:
17.(1)解:如图所示
(2)解:相等,理由如下:
∵ ∠A=90° ,
∴DAAB,
∵BC的垂直平分线为DE
∴DB=DC
∵∠C=30°,∠A=90° ,
∴∠C=∠DBC=30° ,∠ABC=60° ,
∴∠ABD=30° ,
∴BD平分∠ABC
∵DAAB,DEBC,
∴AD=DE
18.解:(1)观察图像,横坐标为学习后的时间x,是自变量;纵坐标是记忆留存率y,是因变量;
故答案为:学习后的时间x;记忆留存率y;
(2) 由图象知,遗忘速度先 快后慢; 记忆留存率随学习后时间的增长而逐渐减少;
故答案为:学习后第1个小时,记忆留在李为44.2%;
19.解:(1)如图3:
①根据长方形的面积公式图3的为:(a+b)(a+2b)
观察图形由1个A为a2,3个C为3ab,2个B为2b2构成,因而可得:(a+2b)(a+b)=a2+3ab+2b2
②∵(a+3b)(a+b)=a2+4ab+3b2
∴需要A型卡片2 张,需要B型卡片3 张,需要C型卡片4 张, 故答案为:①(a+2b)(a+b)=a2+3ab+2b2;②1,3,4;
20.解:(1)∵ △ ABC是等边三角形,
∴AB = BC,∠ABC =∠BAC= 60°,
∵点D为BC中点,
∴∠BAD=∠BAC=30°,AD=,
∵点E为AC中点,
∴∠ABE=∠ABC=30°,BE=,
∴AD=BE,
∴∠AOE=∠ABE+∠BAD=60°,
故答案为:AD=BE ,60°;
(3) ①∵PQ// BE ,MN//AD,
∴∠EMF=∠EAO,∠EFM=∠AOE,
在 △ MEF中,∠MFE+∠EMF+∠MEF= 180° ,
在△AEO中, ∠AOE+∠EAO+∠AEO= 180° ,
∴∠MFE=∠AOE,
由(2)得,∠AOE= 60°,
∴∠MFE=60°,
故答案为:60°.
一、选择题(本题共有8小题,每小题3分,共24分,每小题有4个选项,其中只有一个是正确的)
1.下列四种中国古代青铜器上的纹饰中,是轴对称图形的是( )
A. B.
C. D.
2.下列运算中正确的是( )
A. B.
C. D.
3.如图,小明将一块直角三角板摆放在直尺上,直角顶点落在直尺的边上。若∠1=55°,则∠2的度数为( )
A.255° B.35° C.455° D.555°
4.下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
5.茶文化是中国对茶认识的一种具体表现,其内涵与茶具设计之间存在着密不可分的联系。如图,向茶杯中匀速注水,下列哪幅图象能较好刻画出茶杯中水面高度的变化情况( )
A. B.
C. D.
6.在体育课上,老师组织同学们进行跳远练习,如图是小深跳远时沙坑的示意图,测量成须时先用皮尺从后脚印的点A处垂直拉至起跳线1的点B处,然后记录AB的长度,这样做的道理是( )
A.两点之间,线段最短: B.过两点有且只有一条直线;
C.垂线段最短; D.过一点可以作无数条直线。
7.如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接最出A,B间的距离。为此,小明和小华两位同学提供了如下测量方案:
方案1 ①如图1,选定点O; ②连接AO,并延长到点C,使OC=OA,连接BO,并延长到点D,使OD=OB: ③连接DC,测量DC的长度即可。 方案2 ①如图2,选定点O: ②连接AO,BO,并分别延长到点F,E,使OF=OB,OE=OA: ③连接EF,测量EF的长度即可。
对于方案1和方案2,下列说法正确的是( )
A.1、2都不可行 B.1不可行、2可行
C.1可行、2不可行 D.1、2都可行
8.如果将(a+b)n(n为非负整数)的展开式每一项按字母ɑ的次数由大到小排列,就可以得到下面的等式:
观察上述每个式子的各项系数,我们可以得到如右图所示的数表,这就是我国南宋数学家杨辉在其著作《详解九章算法》中提到的数表“杨辉三角”,他揭示了(a+b)n展开后的各项系数的规律。根据这个表,(a+b)7的展开式中所有项系数的和为( )
A.128 B.256 C.512 D.108
二、填空题(每小题3分,共15分,请将正确的答案填在答题卡上)
9.若am=2,a"=8,则am+n= 。
10.一个不透明的袋子里装有红、蓝两种颜色的球共40个,每个球除颜色外都相同,每次摸球前先把球摇匀,从中随机摸出一个球,记下它的颜色后再放回袋子里,不断重复这一过程,将实验后的数据整理成下表:
摸球次数 50 100 200 500 800 1000
摸到红球的频数 11 27 50 124 201 249
摸到红球的频率 0.220 0.270 0.250 0.248 0.251 0.249
请估计袋中红球的个数是 。
11.如图,在Rt△ABC中,∠C=90°,∠B=52°,D、E分别在AB、AC上,将ADE沿DE折叠得到△FDE,且满足EF//AB,则∠EDF= .
12.小南设计了如下的运算程序:任意写下一个三位数(三位数字相同的除外),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大的数减去最小的数,得到差。重复这个过程,则按照此程序运算2025次后得到的数是 。
13.如图,在△ABC中,AC⊥BC,AC=BC,点D在△ABC内部,且满足∠ADC=90°,若CD=6,则△BCD的面积为 .
三、解答题(本题共7小题,其中第14题8分,第15题7分,第16题8分,第17题9分,第18题9分,第19题10分,第20题10分,共61分)
14.计算
(1);
(2)。
15.化简与求值:
[(2a+b)2-(2a+b)(2a-b)]÷2b,其中a=2,b=-1。
16.如图所示,在正方形网格中,每个小正方形的边长为1个单位长度。
(1)请画出四边形ABCD关于直线m成轴对称的四边形A'B'C'D':
(2)请在直线m上确定一点P,使PC+PD最短。
17.如图,在Rt△ABC中,∠A=90°,∠C=30°。
(1)请用尺规作线段BC的垂直平分线,交AC于点D,交BC于点B:(保留作图痕迹,不用写作法)
(2)在(1)的条件下,AD和DE相等吗?请说明理由。
18.如果不复习,学习过的知识会随时间的推移而逐渐被遗忘。德国心理学家艾宾浩斯最早研究了记忆遗忘规律。他根据自己得到的测试数据描绘了一条曲线(如图所示),这就是艾宾浩斯遗忘曲线。
观察图象,回答下列问题:
(1)自变量是 ,因变量是 .
(2)由图象知,遗忘速度先 后 ;记忆留存率随学习后时间的增长而逐渐 .
(3)请说明图中点B的实际意义:
(4)有研究表明,如及时复习,经过一天记忆能保持98%。由此,你对数学学习有什么感悟?
19.综合与实践
数形结合是一种重要的数学思想方法,借助图形的直观性,可以对很多数学问题进行直观推导。在学习整式乘法运算时,启航小组同学利用图1所示的正方形和长方形卡片拼成了如图2所示的大正方形,发现这个图形可以直观解释完全平方公式:(a+b)2=a2+2ab+b2。
(1)【初步体验】
①领航小组同学拼出了如图3所示的长方形,这个图形可以解释的等式为 .
②护航小组同学要拼成一个长为(a+3b),宽为(a+b)的长方形,那么需要A型卡片 张,B型卡片 张,C型卡片 张:
(2)【实践操作】
从A,B,C三种卡片中选取几张,用它们拼成一个面积为(2a2+5ab+2b2)的长方形,请在图4方框中画出你的拼图:
(3)【实践探究】
远航小组同学用5张C类卡片按图5所示方式不重叠地放在长方形BFGH内,阴影部分的面积S1与S2的差与EH的长度无关,设EH的长为x,请探究a与b的数量关系,并说明理由。
20.在面对复杂数学问题时,“特殊化与转化”是重要的问题解决策略。从特殊图形出发,将新研究的问题转化为以前研究过的熟悉的问题,将一般转化为特殊,有助于我们发现解决问题的思路。
【问题背景】
如图1,在等边△ABC中,D、E分别为边BC、AC上任意一点,且BD=CE,连接AD、BE,AD与BE相交于点O。
(1)【特例感知】
当点D为BC中点,点E为AC中点时,请直按写出线段AD与BE的数量关系 ,∠AOE= ;
(2)【一般探究】
当D、E分别为边BC,AC上任意一点时,第一问的结论还成立吗?请说明理由:
(3)【拓展延伸】
如图2,在等边△ABC中,P、M分别为边AB、AC上的点,且AM=BP,过点P作PQ//BE交AC于点Q,交AD于点G;过点M作MN∥AD交BC于点N,交BE于点F,则
①∠MFE= .
②求证:PQ=MN。
答案解析部分
1.解:A、 不是轴对称图形,故A不符合题意;
B、是轴对称图形,故B符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意;
故答案为:B.
2.解:A、,计算错误,故A不符合题意;
B、,计算错误,故B不符合题意;
C、,计算错误,故C不符合题意;
D、 ,计算正确,故D符合题意;
故答案为:D.
3.解:如图,∵∠1=55°,AB//CD,
∴∠3=∠1 =55°,
∴∠2= 180-90-∠3=35°.
故答案为:B.
4.解:A、随机事件是指在一定条件下可能发生也可能不发生的事件,掷3颗骰子,3颗全是6点朝上是可能发生但不必然发生的事件,因此属于随机事件,故A正确;
B、从1,2,3,4,5中随机抽取一个数,偶数为2和4,共2个,概率应为,故B错误;
C、买中国福利彩票中奖是可能发生但非必然发生的事件,属于随机事件,而非必然事件,故C错误
D、拋硬币正面朝上的概率为,连续抛2次的结果可能为(正正)、 (正反)、(反正)、(反反),其中“必有1次正面”不成立(如两次均为反面),故D错误;
故答案为:A.
5.解:∵茶杯下细上粗,
∴水面高度在茶杯中上升的速度先快后慢;
故答案为:B.
6.解:这样做的理由是垂线段最短,
故答案为:C.
7.解:方案1:在△AOB与△COD中,
AO=OC,AOB=COD,OB= OD,
∴△AOB△COD(SAS),
∴AB=CD.
方案2:在△AOB与△EOF中,
AO=EО,
AOB=EOF,
OB=OF
∴△AOB△EOF(SAS),
∴AB=EF.
故答案为:D.
8.解:当n=0时,展开式中所有项的系数和为1,
当n= 1时,展开式中所有项的系数和为2=2' ,
当n=2时,展开式中所有项的系数和为4=22 ,
当n=3时,展开式中所有项的系数和为8=23,
由此可知(a+b)n展开式中所有项的系数和为2n,
则(a+b)7展开式中所有项的系数和是27=128.
故答案为:A.
9.解: ∵ am+n= am an, 且am=2,an=8
∴ am+n=2
故答案为:16.
10.解:观察表格中数据,随着摸球次数增加(500次及以上), 摸到红球的频率稳定在0.25左右,因此可估计摸到红球的概率约为0.25,
设袋中红球个数为x总球数为40得到:,
解得x=10
故答案为:10.
11.解:如图:
∵∠C=90°,∠B=52°,
∴∠A=38°,
∵EF//AB
∴∠BDF=∠A=32°
由折叠的性质得∠EDF=∠ADE,
∴ ∠EDF=71°
故答案为:71°.
12.解:根据题干任意写下一个三位数(三位数字相同的除外)
以三位数321为例:
1.最大数: 321,最小:123 差: 321 - 123= 198,
2.最大数:981,最小数: 189差: 981- 189= 792,
3.最大数: 972,最小数: 279差: 972 - 279=693,
4.最大数: 963, 最小数: 369差:963- 369= 594
5.最大数: 954, 最小数: 459差: 954-459= 495,
6.最大数:954,最小数: 459差: 954-459= 495 ,
开始重复我们发现,从第5步开始,结果稳定在495
故答案为:495.
13.解:如图:过点B作CD延长线的垂线交于点E,
∵BECD, AD⊥DC
∴ADC=BEC
∵AC⊥BC
∴ACD+BCE=90;ACD+CBE=90;
∴ACD=EBC,
∵AC=BC,
∴
∴BE=CD=6,
∴ △BCD的面积.
故答案为:18.
14.(1)解:原式=-1-1+2
=0
(2)解:原式=4x4y2
=-4xy
15.解:原式=(4a2+4ab+b2-4a2+b2)
=(4ab+2b2)
=2a+b
当a=2,b=-1时,
原式==3
16.(1)解:如图:
(2)解:如图:
17.(1)解:如图所示
(2)解:相等,理由如下:
∵ ∠A=90° ,
∴DAAB,
∵BC的垂直平分线为DE
∴DB=DC
∵∠C=30°,∠A=90° ,
∴∠C=∠DBC=30° ,∠ABC=60° ,
∴∠ABD=30° ,
∴BD平分∠ABC
∵DAAB,DEBC,
∴AD=DE
18.解:(1)观察图像,横坐标为学习后的时间x,是自变量;纵坐标是记忆留存率y,是因变量;
故答案为:学习后的时间x;记忆留存率y;
(2) 由图象知,遗忘速度先 快后慢; 记忆留存率随学习后时间的增长而逐渐减少;
故答案为:学习后第1个小时,记忆留在李为44.2%;
19.解:(1)如图3:
①根据长方形的面积公式图3的为:(a+b)(a+2b)
观察图形由1个A为a2,3个C为3ab,2个B为2b2构成,因而可得:(a+2b)(a+b)=a2+3ab+2b2
②∵(a+3b)(a+b)=a2+4ab+3b2
∴需要A型卡片2 张,需要B型卡片3 张,需要C型卡片4 张, 故答案为:①(a+2b)(a+b)=a2+3ab+2b2;②1,3,4;
20.解:(1)∵ △ ABC是等边三角形,
∴AB = BC,∠ABC =∠BAC= 60°,
∵点D为BC中点,
∴∠BAD=∠BAC=30°,AD=,
∵点E为AC中点,
∴∠ABE=∠ABC=30°,BE=,
∴AD=BE,
∴∠AOE=∠ABE+∠BAD=60°,
故答案为:AD=BE ,60°;
(3) ①∵PQ// BE ,MN//AD,
∴∠EMF=∠EAO,∠EFM=∠AOE,
在 △ MEF中,∠MFE+∠EMF+∠MEF= 180° ,
在△AEO中, ∠AOE+∠EAO+∠AEO= 180° ,
∴∠MFE=∠AOE,
由(2)得,∠AOE= 60°,
∴∠MFE=60°,
故答案为:60°.
同课章节目录
