浙江省宁波市强基计划2025年数学测试试卷(含答案)
文档属性
| 名称 | 浙江省宁波市强基计划2025年数学测试试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 491.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 10:48:09 | ||
图片预览




文档简介
浙江省宁波市强基计划2025年数学测试试卷
一、选择题(共4小题)
1.已知,下面结论正确的是( )
A. B. C. D.
2.甲盒子里有2个白球,乙盒子中有3个白球,丙盒子中有3个白球和1个黑球,问随机选一个盒子,随机摸一个球,摸出黑色小球的概率为( )
A. B. C. D.
3.已知为等腰三角形,,点为的内心,点为的外心,则OI的值为( )
A. B. C. D.
4.已知,设的最大值为,则的最小值为( )
A. B.7 C. D.9
二、填空题(共5小题)
5.化简: .
6.已知函数,则该函数与坐标轴围成的面积为 .
7.已知a,b满足,已知为正数,则 .
8.如图,已知为四边形ABCD的内接圆,恰好与三条边相切,半径为为四边形ABCD的外接圆,半径为,则的取值范围为 .
9.如图,已知点在反比例函数的图象上,为直角三角形,将旋转至,使得点恰好也在反比例函数的图象上,已知,则的值为 .
三、解答题(共3小题)
10.已知
(1)当时,求的最小值.
(2)当为正整数时,求abc的值.
(3)是否存在a,b,c为整数,使的值为奇数.若存在,请求出的值;若不存在,请说明理由.
11.(1)在四边形ABED中,,在BC上有一点,连结,.证明:.
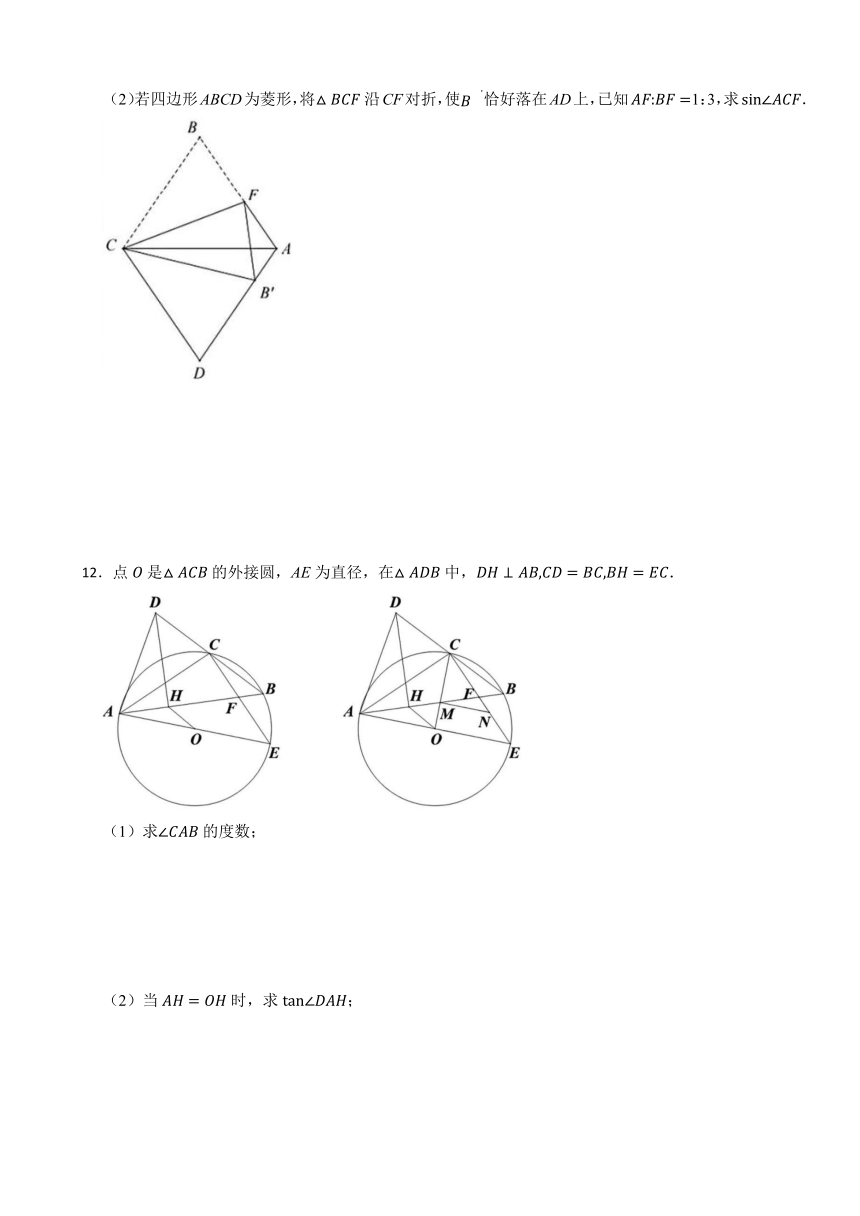
(2)若四边形ABCD为菱形,将沿CF对折,使恰好落在AD上,已知1:3,求.
12.点是的外接圆,AE为直径,在中,.
(1)求的度数;
(2)当时,求;
(3)连结OC交AB于点,过点作交EF于点,探究CF,FM,MN三者之间的数量关系.
答案解析部分
1.解:把消去b可得a=c+4,
又∵b=3a-4≥0,
解得,
∴c+4≥,
解得:
故答案为:D.
2.解:先选盒子选中丙盒子的可能性为,从中选中黑球的可能性为,
∴ 摸出黑色小球的概率为
故答案为:D.
3.解:过点A作AD⊥BC于点D,连BO,
则AD平分∠BAC,且BD=CD=3,
∴点I和O都在AD上,
∴AO=OB
,
在Rt△BOD中,,即,
解得OD=,
设内切圆的半径ID为r,则,
即,
解得,
∴,
故答案为:B.
4.解:,
∴当时,即x=-时y取得最小值,
∵开口向上,
∴y随x的增大而增大,
即当x=3时,y有最大值,M=,
∴M的最小值为,
故答案为:C.
5.解:
故答案为:.
6.解:当x<1时,y=3-x+x-1=2,与y轴交于点(0,2),
当1≤x≤3时,y=3-x-x+1=-2x+4,与想轴交于点(2,0),
当x>3时,y=x-3-x+1=-2,与轴没有交点;
∴ 该函数与坐标轴围成的梯形面积为,
故答案为:3.
7.解:由题可得,
即,
∴
解得:或(舍去)
故答案为: .
8.解:①如图,当点重合时,有是的内切圆,设与相切于点,
∴,平分,,
∴是等边三角形,,
∴,
∴,
∴;
②如图,当与四边形四边相切时,设与相切于点,连接,
∴,,
∴,四边形是菱形,
∵为四边形的外接圆,且是同心圆,
∴与的交点为,,
∴四边形是正方形,
∴是等腰直角三角形,
∴;
综上所述,的取值范围为,
故答案为:.
9.解:如图,延长交轴于点,过点作于点,连接,过点作轴于点,
∴
∵旋转的性质,,
∴,
∴,
∴,
∵,
∴,
∵点在反比例函数图象上,
∴根据反比例函数的对称性可知,
∴,
由“一线三垂直”全等模型易证,
∴,
设,
∴,
∵,
∴,
∴,
整理得:,
解得:或,
∵,
∴或,
当时,,
∴,
∴,
∴;
当时,同理求出,
∴;
综上所述,的值为或,
故答案为:或.
10.(1)解:当时,,则,
可知当时,.
(2)把和代入得,
整理可得,
由于为正整数,可得=1,
从而
∴.
(3)把代入得,由于与奇偶性不同,与奇偶性不同,故与必定同为偶数,
也必定为偶数.
11.(1)如图,延长BE至点,使得,则∠DEG=∠G,
又∵DE∥AB,
∴∠B=∠DEG=∠G,
又∵∠BAC+∠B=∠ACD+∠DCG,
∴∠BAC=∠DCG,
∵AC=CD,
∴.
(2)延长DA至点G,使得FG=FA,则∠FAG=∠G,
设,则,
由折叠可得∠B=∠CB'F,BC=B'C,
∵ABCD是菱形,
∴CD=CB=CB',CD∥AB,
∴∠D=∠B=∠CB'F=∠FAG=∠G,
∴∠DCB'+∠D=∠CB'F+∠FB'G,
∴∠DCB'=∠FB'G,
∴,
∴,即,
解得,
过作于,得,
由折叠,
.
12.(1)连结OC,OB
为直径,
(ASA)
为等边三角形
(2)连结
、B、D、H四点共圆
为等腰直角三角形
作,则
设,则
.
(3)解:∵∠CAB=30°,∠ACF=90°,
∴,
又∵MN∥AE,
∴∠CMN=∠COE=90°,
又∵∠MAN=45°,
∴,
过点M作MG⊥NC于点G,
则,,
∴,
∴.
一、选择题(共4小题)
1.已知,下面结论正确的是( )
A. B. C. D.
2.甲盒子里有2个白球,乙盒子中有3个白球,丙盒子中有3个白球和1个黑球,问随机选一个盒子,随机摸一个球,摸出黑色小球的概率为( )
A. B. C. D.
3.已知为等腰三角形,,点为的内心,点为的外心,则OI的值为( )
A. B. C. D.
4.已知,设的最大值为,则的最小值为( )
A. B.7 C. D.9
二、填空题(共5小题)
5.化简: .
6.已知函数,则该函数与坐标轴围成的面积为 .
7.已知a,b满足,已知为正数,则 .
8.如图,已知为四边形ABCD的内接圆,恰好与三条边相切,半径为为四边形ABCD的外接圆,半径为,则的取值范围为 .
9.如图,已知点在反比例函数的图象上,为直角三角形,将旋转至,使得点恰好也在反比例函数的图象上,已知,则的值为 .
三、解答题(共3小题)
10.已知
(1)当时,求的最小值.
(2)当为正整数时,求abc的值.
(3)是否存在a,b,c为整数,使的值为奇数.若存在,请求出的值;若不存在,请说明理由.
11.(1)在四边形ABED中,,在BC上有一点,连结,.证明:.
(2)若四边形ABCD为菱形,将沿CF对折,使恰好落在AD上,已知1:3,求.
12.点是的外接圆,AE为直径,在中,.
(1)求的度数;
(2)当时,求;
(3)连结OC交AB于点,过点作交EF于点,探究CF,FM,MN三者之间的数量关系.
答案解析部分
1.解:把消去b可得a=c+4,
又∵b=3a-4≥0,
解得,
∴c+4≥,
解得:
故答案为:D.
2.解:先选盒子选中丙盒子的可能性为,从中选中黑球的可能性为,
∴ 摸出黑色小球的概率为
故答案为:D.
3.解:过点A作AD⊥BC于点D,连BO,
则AD平分∠BAC,且BD=CD=3,
∴点I和O都在AD上,
∴AO=OB
,
在Rt△BOD中,,即,
解得OD=,
设内切圆的半径ID为r,则,
即,
解得,
∴,
故答案为:B.
4.解:,
∴当时,即x=-时y取得最小值,
∵开口向上,
∴y随x的增大而增大,
即当x=3时,y有最大值,M=,
∴M的最小值为,
故答案为:C.
5.解:
故答案为:.
6.解:当x<1时,y=3-x+x-1=2,与y轴交于点(0,2),
当1≤x≤3时,y=3-x-x+1=-2x+4,与想轴交于点(2,0),
当x>3时,y=x-3-x+1=-2,与轴没有交点;
∴ 该函数与坐标轴围成的梯形面积为,
故答案为:3.
7.解:由题可得,
即,
∴
解得:或(舍去)
故答案为: .
8.解:①如图,当点重合时,有是的内切圆,设与相切于点,
∴,平分,,
∴是等边三角形,,
∴,
∴,
∴;
②如图,当与四边形四边相切时,设与相切于点,连接,
∴,,
∴,四边形是菱形,
∵为四边形的外接圆,且是同心圆,
∴与的交点为,,
∴四边形是正方形,
∴是等腰直角三角形,
∴;
综上所述,的取值范围为,
故答案为:.
9.解:如图,延长交轴于点,过点作于点,连接,过点作轴于点,
∴
∵旋转的性质,,
∴,
∴,
∴,
∵,
∴,
∵点在反比例函数图象上,
∴根据反比例函数的对称性可知,
∴,
由“一线三垂直”全等模型易证,
∴,
设,
∴,
∵,
∴,
∴,
整理得:,
解得:或,
∵,
∴或,
当时,,
∴,
∴,
∴;
当时,同理求出,
∴;
综上所述,的值为或,
故答案为:或.
10.(1)解:当时,,则,
可知当时,.
(2)把和代入得,
整理可得,
由于为正整数,可得=1,
从而
∴.
(3)把代入得,由于与奇偶性不同,与奇偶性不同,故与必定同为偶数,
也必定为偶数.
11.(1)如图,延长BE至点,使得,则∠DEG=∠G,
又∵DE∥AB,
∴∠B=∠DEG=∠G,
又∵∠BAC+∠B=∠ACD+∠DCG,
∴∠BAC=∠DCG,
∵AC=CD,
∴.
(2)延长DA至点G,使得FG=FA,则∠FAG=∠G,
设,则,
由折叠可得∠B=∠CB'F,BC=B'C,
∵ABCD是菱形,
∴CD=CB=CB',CD∥AB,
∴∠D=∠B=∠CB'F=∠FAG=∠G,
∴∠DCB'+∠D=∠CB'F+∠FB'G,
∴∠DCB'=∠FB'G,
∴,
∴,即,
解得,
过作于,得,
由折叠,
.
12.(1)连结OC,OB
为直径,
(ASA)
为等边三角形
(2)连结
、B、D、H四点共圆
为等腰直角三角形
作,则
设,则
.
(3)解:∵∠CAB=30°,∠ACF=90°,
∴,
又∵MN∥AE,
∴∠CMN=∠COE=90°,
又∵∠MAN=45°,
∴,
过点M作MG⊥NC于点G,
则,,
∴,
∴.
同课章节目录
