北京市清华附中2024-2025学年新高一分班考数学试卷(含答案)
文档属性
| 名称 | 北京市清华附中2024-2025学年新高一分班考数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览

文档简介
北京清华附中2024-2025学年新高一分班考数学试卷
(满分150分,考试时间120 分钟)
题号 一 二 三 总分
得分
一、选择题(每题5分,共40分)
1.化简 ( )
A. √a B. - a C. a D. a
2.分式 的值为0,则x的值为 ( )
A. - 1或2 B. 2 C. - 1 D. - 2
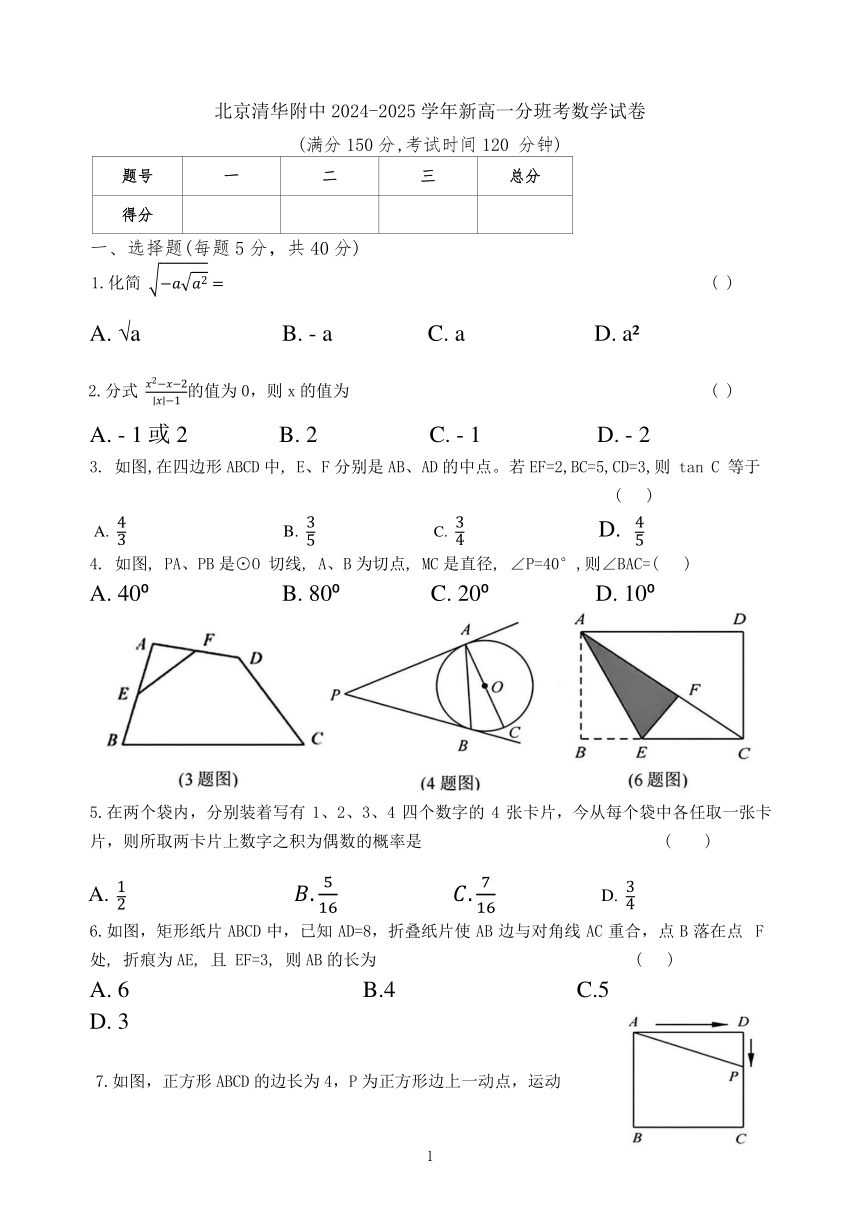
3. 如图,在四边形ABCD中, E、F分别是AB、AD的中点。若EF=2,BC=5,CD=3,则 tan C 等于 ( )
A. B. C. D.
4. 如图, PA、PB是⊙O 切线, A、B为切点, MC是直径, ∠P=40°,则∠BAC=( )
A. 40 B. 80 C. 20 D. 10
5.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是 ( )
A. D.
6.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点 F 处, 折痕为AE, 且 EF=3, 则AB的长为 ( )
A. 6 B.4 C.5
D. 3
7.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动
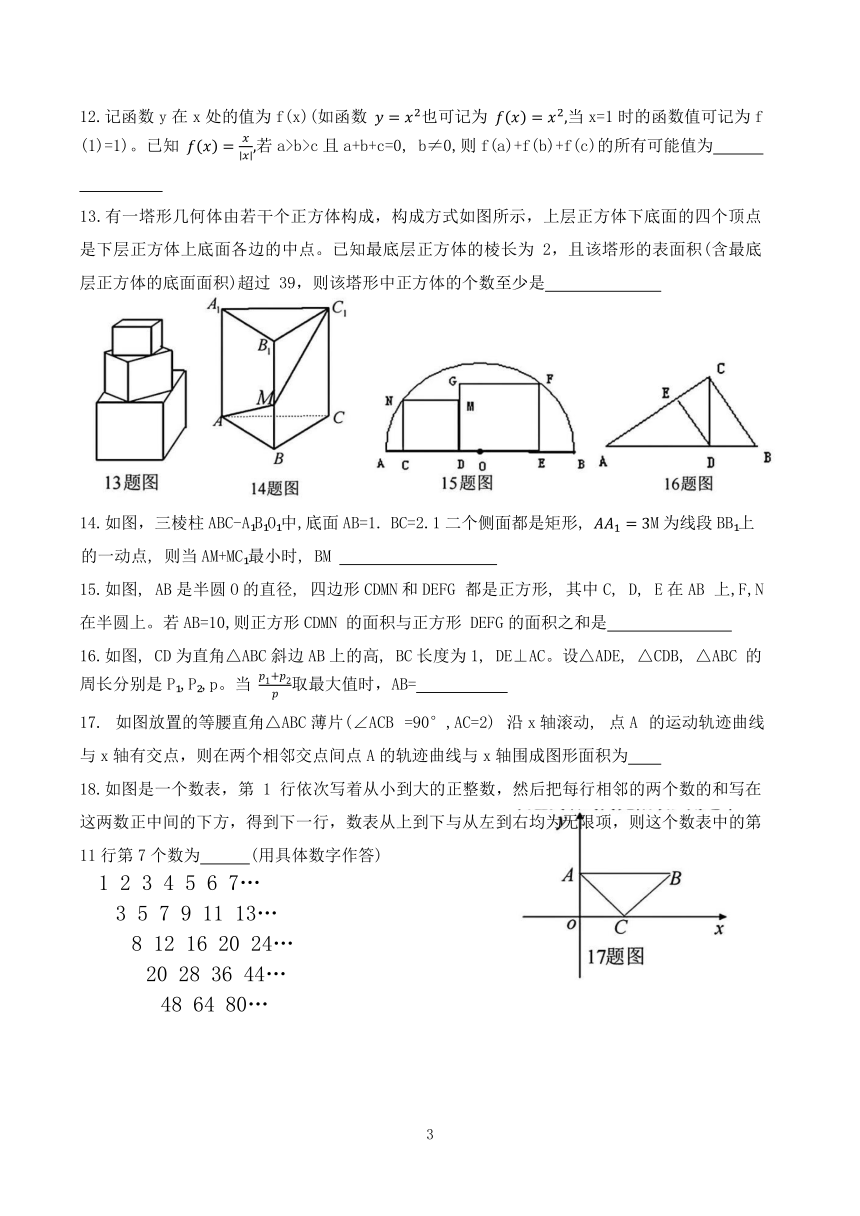
路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下 列 图 象 能 大 致 反 映 y 与 x 的 函 数 关 系 的 是( )
8.若直角坐标系内两点 P、Q满足条件①P、Q都在函数y的图象上②P、Q关于原点对称,则称点对(P,Q)是函数y的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”)。已知函数 则函数y的“友好点对”有()个
A. 0 B.1 C.2 D.3
注意:请将选择题的答案填入表格中。
题号 1 2 3 4 5 6 7 8 得分 评卷人
答案
二、填空题(每题5分,共50分)
9.已知a、b是一元二次方程 的两个实数根,则代数式(a-b)(a+b-2)+ ab的值等于
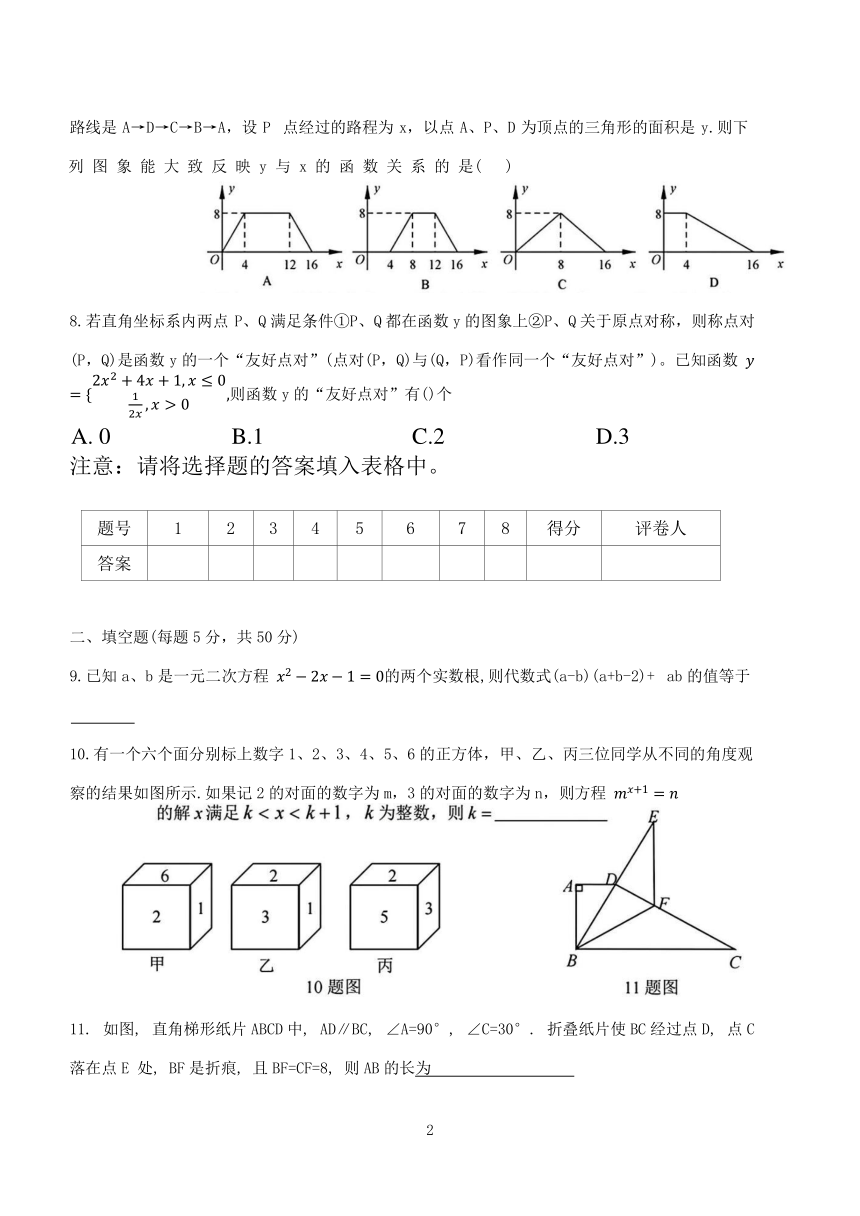
10.有一个六个面分别标上数字1、2、3、4、5、6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m,3的对面的数字为n,则方程
11. 如图, 直角梯形纸片ABCD中, AD∥BC, ∠A=90°, ∠C=30°. 折叠纸片使BC经过点D, 点C落在点E 处, BF是折痕, 且BF=CF=8, 则AB的长为
12.记函数y在x处的值为f(x)(如函数 也可记为 当x=1时的函数值可记为f(1)=1)。已知 若a>b>c且a+b+c=0, b≠0,则f(a)+f(b)+f(c)的所有可能值为
13.有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过 39,则该塔形中正方体的个数至少是
14.如图,三棱柱ABC-A B O 中,底面AB=1. BC=2.1二个侧面都是矩形, M为线段BB 上的一动点, 则当AM+MC 最小时, BM
15.如图, AB是半圆O的直径, 四边形CDMN和DEFG 都是正方形, 其中C, D, E在AB 上,F,N在半圆上。若AB=10,则正方形CDMN 的面积与正方形 DEFG的面积之和是
16.如图, CD为直角△ABC斜边AB上的高, BC长度为1, DE⊥AC。设△ADE, △CDB, △ABC 的周长分别是P ,P ,p。当 取最大值时,AB=
17. 如图放置的等腰直角△ABC薄片(∠ACB =90°,AC=2) 沿x轴滚动, 点A 的运动轨迹曲线与x轴有交点,则在两个相邻交点间点A的轨迹曲线与x轴围成图形面积为
18.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,则这个数表中的第11行第7个数为 (用具体数字作答)
1 2 3 4 5 6 7…
3 5 7 9 11 13…
8 12 16 20 24…
20 28 36 44…
48 64 80…
得分 评卷人
11. 12.
13. 14. 15.
16. 18. 17.
三、解答题(共60分)
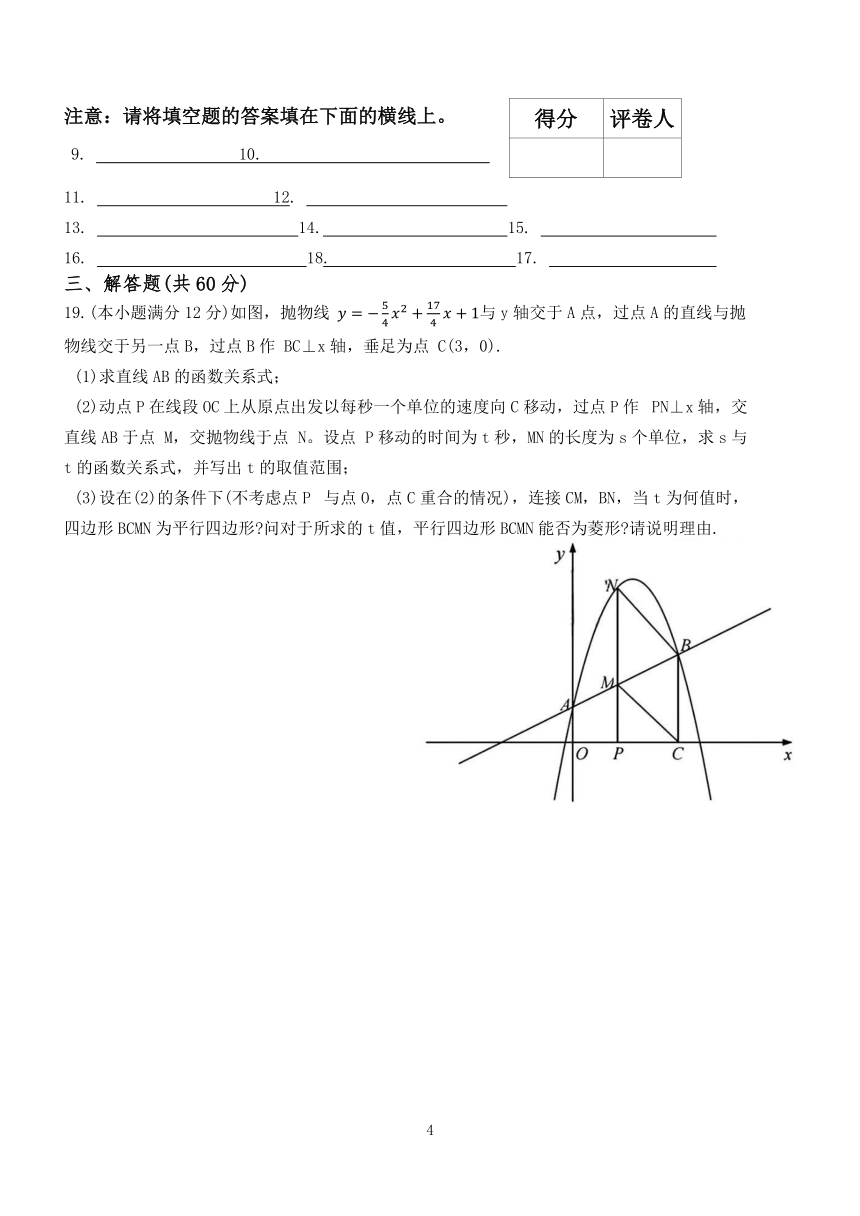
19.(本小题满分12分)如图,抛物线 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作 BC⊥x轴,垂足为点 C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作 PN⊥x轴,交直线AB于点 M,交抛物线于点 N。设点 P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P 与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形 问对于所求的t值,平行四边形BCMN能否为菱形 请说明理由.
20.(本小题满分12分)函数f(x),若自变量x取值范围内存在x ,使 成立,则称以( 为坐标的点为函数 f(x)图像上的不动点。(f(x)的定义见第12题)
(1)若函数 有两个关于原点对称的不动点,求a,b应满足的条件;
(2) 在(1) 的条件下, 若a=2,直线l:y=(1-a)x+b-1与y轴、x轴分别相交于A、B两点,在 的图象上取一点 P(P点的横坐标大于2),过P作. 轴,垂足是Q,若四边形 ABQP 的面积等于2,求 P 点的坐标
(3)定义在实数集上的函数f(x),对任意的x有. 恒成立。下述命题“若函数f(x)的图像上存在有限个不动点,则不动点有奇数个”是否正确 若正确,给予证明;若不正确,举反例说明。
21.(本小题满分12分)已知圆O圆心为坐标原点,半径为 直线l: 交x轴负半轴于A点,交y轴正半轴于B点
(1) 求
(2)设圆O与x轴的两交点是 若从 发出的光线经l上的点 M反射后过点 求光线从. 射出经反射到 经过的路程
(3)点P是x轴负半轴上一点,从点P发出的光线经l反射后与圆O相切.若光线从射出经反射到相切经过的路程最短,求点 P 的坐标
22. (本小题满分12分)
在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.
(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢
(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层,
(Ⅰ)共有几种不同的方案
(Ⅱ)已知每根圆钢的直径为10cm,为考虑安全隐患,堆放高度不得高于4m,则选择哪个方案,最能节省堆放场地
23. (本小题满分12分)
试求出所有正整数a使得关于x的二次方程 至少有一个整数根.
2020北京清华附中新高一分班考试
1-8 BBACAD ABC
9.-1
10. 0
11. 6
12.1或-1
13. 6
14. 1
15. 25
16. 2
17. 4π+2
18. 12288
19.(1) y=x/2+1
(3) t=1
20. (1)b=3, a>0且a≠9
(2) (5/2, 6/5)
(3) 正确
21. (1)30°
(2) 8/3
(3) (-2, 0)
22. 62层时, 剩56根圆钢
4种, n=7, 14, 41, 49
堆放41层,最节省
23. 4个, a=1, 3, 6, 10
(满分150分,考试时间120 分钟)
题号 一 二 三 总分
得分
一、选择题(每题5分,共40分)
1.化简 ( )
A. √a B. - a C. a D. a
2.分式 的值为0,则x的值为 ( )
A. - 1或2 B. 2 C. - 1 D. - 2
3. 如图,在四边形ABCD中, E、F分别是AB、AD的中点。若EF=2,BC=5,CD=3,则 tan C 等于 ( )
A. B. C. D.
4. 如图, PA、PB是⊙O 切线, A、B为切点, MC是直径, ∠P=40°,则∠BAC=( )
A. 40 B. 80 C. 20 D. 10
5.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是 ( )
A. D.
6.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点 F 处, 折痕为AE, 且 EF=3, 则AB的长为 ( )
A. 6 B.4 C.5
D. 3
7.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动
路线是A→D→C→B→A,设P 点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下 列 图 象 能 大 致 反 映 y 与 x 的 函 数 关 系 的 是( )
8.若直角坐标系内两点 P、Q满足条件①P、Q都在函数y的图象上②P、Q关于原点对称,则称点对(P,Q)是函数y的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”)。已知函数 则函数y的“友好点对”有()个
A. 0 B.1 C.2 D.3
注意:请将选择题的答案填入表格中。
题号 1 2 3 4 5 6 7 8 得分 评卷人
答案
二、填空题(每题5分,共50分)
9.已知a、b是一元二次方程 的两个实数根,则代数式(a-b)(a+b-2)+ ab的值等于
10.有一个六个面分别标上数字1、2、3、4、5、6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m,3的对面的数字为n,则方程
11. 如图, 直角梯形纸片ABCD中, AD∥BC, ∠A=90°, ∠C=30°. 折叠纸片使BC经过点D, 点C落在点E 处, BF是折痕, 且BF=CF=8, 则AB的长为
12.记函数y在x处的值为f(x)(如函数 也可记为 当x=1时的函数值可记为f(1)=1)。已知 若a>b>c且a+b+c=0, b≠0,则f(a)+f(b)+f(c)的所有可能值为
13.有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过 39,则该塔形中正方体的个数至少是
14.如图,三棱柱ABC-A B O 中,底面AB=1. BC=2.1二个侧面都是矩形, M为线段BB 上的一动点, 则当AM+MC 最小时, BM
15.如图, AB是半圆O的直径, 四边形CDMN和DEFG 都是正方形, 其中C, D, E在AB 上,F,N在半圆上。若AB=10,则正方形CDMN 的面积与正方形 DEFG的面积之和是
16.如图, CD为直角△ABC斜边AB上的高, BC长度为1, DE⊥AC。设△ADE, △CDB, △ABC 的周长分别是P ,P ,p。当 取最大值时,AB=
17. 如图放置的等腰直角△ABC薄片(∠ACB =90°,AC=2) 沿x轴滚动, 点A 的运动轨迹曲线与x轴有交点,则在两个相邻交点间点A的轨迹曲线与x轴围成图形面积为
18.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,则这个数表中的第11行第7个数为 (用具体数字作答)
1 2 3 4 5 6 7…
3 5 7 9 11 13…
8 12 16 20 24…
20 28 36 44…
48 64 80…
得分 评卷人
11. 12.
13. 14. 15.
16. 18. 17.
三、解答题(共60分)
19.(本小题满分12分)如图,抛物线 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作 BC⊥x轴,垂足为点 C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作 PN⊥x轴,交直线AB于点 M,交抛物线于点 N。设点 P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P 与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形 问对于所求的t值,平行四边形BCMN能否为菱形 请说明理由.
20.(本小题满分12分)函数f(x),若自变量x取值范围内存在x ,使 成立,则称以( 为坐标的点为函数 f(x)图像上的不动点。(f(x)的定义见第12题)
(1)若函数 有两个关于原点对称的不动点,求a,b应满足的条件;
(2) 在(1) 的条件下, 若a=2,直线l:y=(1-a)x+b-1与y轴、x轴分别相交于A、B两点,在 的图象上取一点 P(P点的横坐标大于2),过P作. 轴,垂足是Q,若四边形 ABQP 的面积等于2,求 P 点的坐标
(3)定义在实数集上的函数f(x),对任意的x有. 恒成立。下述命题“若函数f(x)的图像上存在有限个不动点,则不动点有奇数个”是否正确 若正确,给予证明;若不正确,举反例说明。
21.(本小题满分12分)已知圆O圆心为坐标原点,半径为 直线l: 交x轴负半轴于A点,交y轴正半轴于B点
(1) 求
(2)设圆O与x轴的两交点是 若从 发出的光线经l上的点 M反射后过点 求光线从. 射出经反射到 经过的路程
(3)点P是x轴负半轴上一点,从点P发出的光线经l反射后与圆O相切.若光线从射出经反射到相切经过的路程最短,求点 P 的坐标
22. (本小题满分12分)
在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.
(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢
(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层,
(Ⅰ)共有几种不同的方案
(Ⅱ)已知每根圆钢的直径为10cm,为考虑安全隐患,堆放高度不得高于4m,则选择哪个方案,最能节省堆放场地
23. (本小题满分12分)
试求出所有正整数a使得关于x的二次方程 至少有一个整数根.
2020北京清华附中新高一分班考试
1-8 BBACAD ABC
9.-1
10. 0
11. 6
12.1或-1
13. 6
14. 1
15. 25
16. 2
17. 4π+2
18. 12288
19.(1) y=x/2+1
(3) t=1
20. (1)b=3, a>0且a≠9
(2) (5/2, 6/5)
(3) 正确
21. (1)30°
(2) 8/3
(3) (-2, 0)
22. 62层时, 剩56根圆钢
4种, n=7, 14, 41, 49
堆放41层,最节省
23. 4个, a=1, 3, 6, 10
同课章节目录
