第二章 电磁感应及其应用 综合拔高练(含答案解析)
文档属性
| 名称 | 第二章 电磁感应及其应用 综合拔高练(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-22 16:54:00 | ||
图片预览



文档简介
综合拔高练
高考真题练
考点1 安培定则、楞次定律的综合应用
1.(2024广东,4)电磁俘能器可在汽车发动机振动时利用电磁感应发电实现能量回收,结构如图甲所示。两对永磁铁可随发动机一起上下振动,每对永磁铁间有水平方向的匀强磁场,磁感应强度大小均为B。磁场中,边长为L的正方形线圈竖直固定在减震装置上。某时刻磁场分布与线圈位置如图乙所示,永磁铁振动时磁场分界线不会离开线圈。关于图乙中的线圈,下列说法正确的是( )
A.穿过线圈的磁通量为BL2
B.永磁铁相对线圈上升越高,线圈中感应电动势越大
C.永磁铁相对线圈上升越快,线圈中感应电动势越小
D.永磁铁相对线圈下降时,线圈中感应电流的方向为顺时针方向
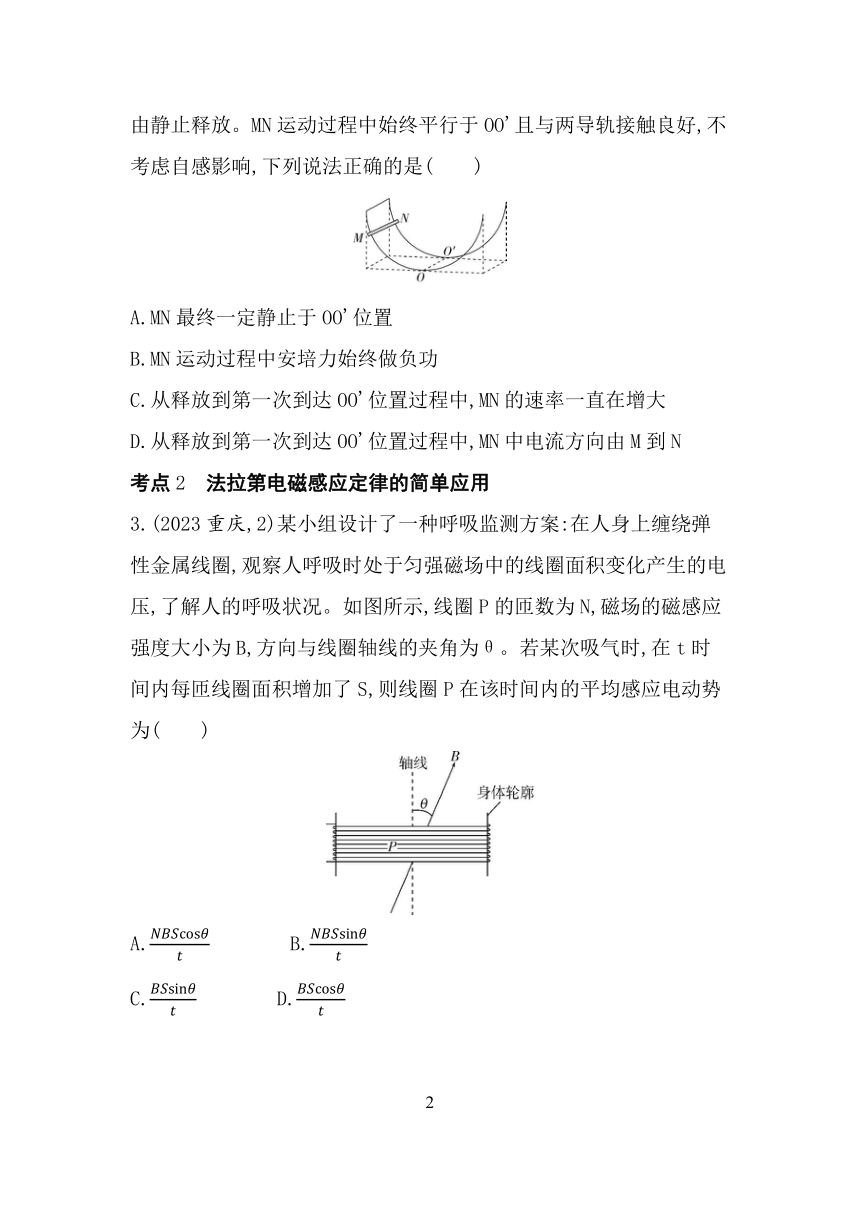
2.(多选题)(2024山东,11)如图所示,两条相同的半圆弧形光滑金属导轨固定在水平桌面上,其所在平面竖直且平行,导轨最高点到水平桌面的距离等于半径,最低点的连线OO'与导轨所在竖直面垂直。空间充满竖直向下的匀强磁场(图中未画出),导轨左端由导线连接。现将具有一定质量和电阻的金属棒MN平行OO'放置在导轨图示位置,由静止释放。MN运动过程中始终平行于OO'且与两导轨接触良好,不考虑自感影响,下列说法正确的是( )
A.MN最终一定静止于OO'位置
B.MN运动过程中安培力始终做负功
C.从释放到第一次到达OO'位置过程中,MN的速率一直在增大
D.从释放到第一次到达OO'位置过程中,MN中电流方向由M到N
考点2 法拉第电磁感应定律的简单应用
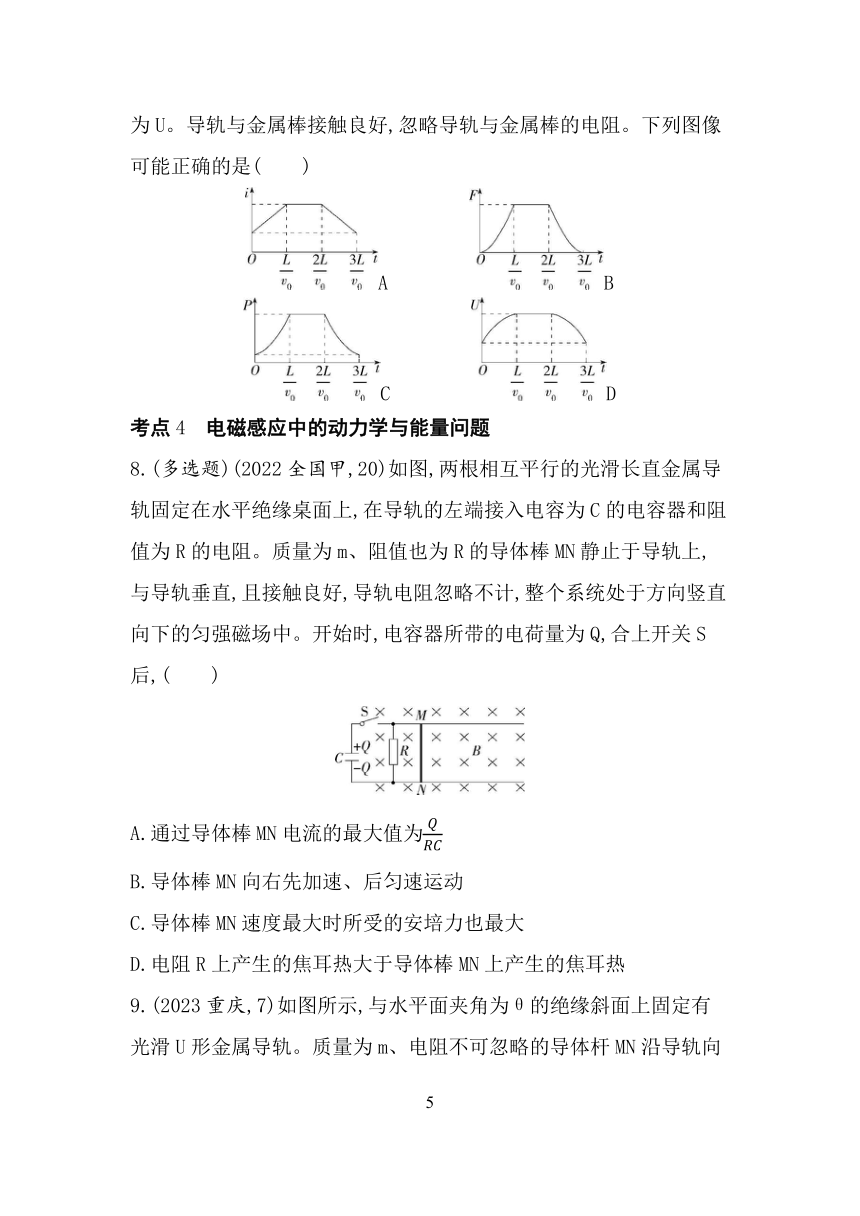
3.(2023重庆,2)某小组设计了一种呼吸监测方案:在人身上缠绕弹性金属线圈,观察人呼吸时处于匀强磁场中的线圈面积变化产生的电压,了解人的呼吸状况。如图所示,线圈P的匝数为N,磁场的磁感应强度大小为B,方向与线圈轴线的夹角为θ。若某次吸气时,在t时间内每匝线圈面积增加了S,则线圈P在该时间内的平均感应电动势为( )
A. B.
C. D.
4.(2024湖南,4)如图,有一硬质导线Oabc,其中是半径为R的半圆弧,b为圆弧的中点,直线段Oa长为R且垂直于直径ac。该导线在纸面内绕O点逆时针转动,导线始终在垂直纸面向里的匀强磁场中。则O、a、b、c各点电势关系为( )
A.φO>φa>φb>φc B.φO<φa<φb<φc
C.φO>φa>φb=φc D.φO<φa<φb=φc
5.(多选题)(2021广东,10)如图所示,水平放置足够长光滑金属导轨abc和de,ab与de平行,bc是以O为圆心的圆弧导轨。圆弧be左侧和扇形Obc内有方向如图的匀强磁场。金属杆OP的O端与e点用导线相接,P端与圆弧bc接触良好。初始时,可滑动的金属杆MN静止在平行导轨上。若杆OP绕O点在匀强磁场区内从b到c匀速转动时,回路中始终有电流,则此过程中,下列说法正确的有( )
A.杆OP产生的感应电动势恒定
B.杆OP受到的安培力不变
C.杆MN做匀加速直线运动
D.杆MN中的电流逐渐减小
6.(2021河北,7)如图,两光滑导轨水平放置在竖直向下的匀强磁场中,磁感应强度大小为B。导轨间距最窄处为一狭缝,取狭缝所在处O点为坐标原点。狭缝右侧两导轨与x轴夹角均为θ,一电容为C的电容器与导轨左端相连。导轨上的金属棒与x轴垂直,在外力F作用下从O点开始以速度v向右做匀速运动,忽略所有电阻。下列说法正确的是( )
A.通过金属棒的电流为2BCv2 tan θ
B.金属棒到达x0时,电容器极板上的电荷量为BCvx0 tan θ
C.金属棒运动过程中,电容器的上极板带负电
D.金属棒运动过程中,外力F做功的功率恒定
考点3 电磁感应中的图像问题
7.(多选题)(2022河北,8)如图,两光滑导轨水平放置在竖直向下的匀强磁场中,一根导轨位于x轴上,另一根由ab、bc、cd三段直导轨组成,其中bc段与x轴平行,导轨左端接入一电阻R。导轨上一金属棒MN沿x轴
正方向以速度v0保持匀速运动,t=0时刻通过坐标原点O,金属棒始终与x轴垂直。设运动过程中通过电阻的电流强度为i,金属棒受到安培力的大小为F,金属棒克服安培力做功的功率为P,电阻两端的电压为U。导轨与金属棒接触良好,忽略导轨与金属棒的电阻。下列图像可能正确的是( )
A B
C D
考点4 电磁感应中的动力学与能量问题
8.(多选题)(2022全国甲,20)如图,两根相互平行的光滑长直金属导轨固定在水平绝缘桌面上,在导轨的左端接入电容为C的电容器和阻值为R的电阻。质量为m、阻值也为R的导体棒MN静止于导轨上,与导轨垂直,且接触良好,导轨电阻忽略不计,整个系统处于方向竖直向下的匀强磁场中。开始时,电容器所带的电荷量为Q,合上开关S后,( )
A.通过导体棒MN电流的最大值为
B.导体棒MN向右先加速、后匀速运动
C.导体棒MN速度最大时所受的安培力也最大
D.电阻R上产生的焦耳热大于导体棒MN上产生的焦耳热
9.(2023重庆,7)如图所示,与水平面夹角为θ的绝缘斜面上固定有光滑U形金属导轨。质量为m、电阻不可忽略的导体杆MN沿导轨向下运动,以大小为v的速度进入方向垂直于导轨平面向下的匀强磁场区域,在磁场中运动一段时间t后,速度大小变为2v。运动过程中杆与导轨垂直并接触良好,导轨的电阻忽略不计,重力加速度为g。杆在磁场中运动的此段时间内( )
A.流过杆的感应电流方向从N到M
B.杆沿轨道下滑的距离为vt
C.流过杆感应电流的平均电功率等于重力的平均功率
D.杆所受安培力的冲量大小为mgt sin θ-mv
10.(多选题)(2024黑吉辽,9)如图,两条“∧”形的光滑平行金属导轨固定在绝缘水平面上,间距为L,左、右两导轨面与水平面夹角均为30°,均处于竖直向上的匀强磁场中,磁感应强度大小分别为2B和B。将有一定阻值的导体棒ab、cd放置在导轨上,同时由静止释放,两棒在下滑过程中始终与导轨垂直并接触良好。ab、cd的质量分别为2m和m,长度均为L。导轨足够长且电阻不计,重力加速度大小为g。两棒在下滑过程中( )
A.回路中的电流方向为abcda
B.ab中电流趋于
C.ab与cd加速度大小之比始终为2∶1
D.两棒产生的电动势始终相等
11.(2023浙江6月选考,10)如图所示,质量为M、电阻为R、长为L的导体棒,通过两根长均为l、质量不计的导电细杆连在等高的两固定点上,固定点间距也为L。细杆通过开关S可与直流电源E0或理想二极管串接。在导体棒所在空间存在磁感应强度方向竖直向上、大小为B的匀强磁场,不计空气阻力和其他电阻。开关S接1,当导体棒静止时,细杆与竖直方向的夹角θ=,重力加速度为g;然后开关S接2,棒从右侧开始运动完成一次振动的过程中( )
A.电源电动势E0=R
B.棒消耗的焦耳热Q=Mgl
C.从左向右运动时,最大摆角小于
D.棒两次过最低点时感应电动势大小相等
12.(2024河北,14)如图,边长为2L的正方形金属细框固定放置在绝缘水平面上,细框中心O处固定一竖直细导体轴OO'。间距为L、与水平面成θ角的平行导轨通过导线分别与细框及导体轴相连。导轨和细框分别处在与各自所在平面垂直的匀强磁场中,磁感应强度大小均为B。足够长的细导体棒OA在水平面内绕O点以角速度ω匀速转动,水平放置在导轨上的导体棒CD始终静止。OA棒在转动过程中,CD棒在所受安培力达到最大和最小时均恰好能静止。已知CD棒在导轨间的电阻值为R,电路中其余部分的电阻均不计,CD棒始终与导轨垂直,各部分始终接触良好,不计空气阻力,重力加速度大小为g。
(1)求CD棒所受安培力的最大值和最小值。
(2)锁定OA棒,推动CD棒下滑,撤去推力瞬间,CD棒的加速度大小为a,所受安培力大小等于(1)问中安培力的最大值,求CD棒与导轨间的动摩擦因数。
13.(2024全国甲,25)两根平行长直光滑金属导轨距离为l,固定在同一水平面(纸面)内,导轨左端接有电容为C的电容器和阻值为R的电阻,开关S与电容器并联;导轨上有一长度略大于l的金属棒,如图所示。导轨所处区域有方向垂直于纸面、磁感应强度大小为B的匀强磁场。开关S闭合。金属棒在恒定的外力作用下由静止开始加速,最后将做速率为v0的匀速直线运动。金属棒始终与两导轨垂直且接触良好,导轨电阻和金属棒电阻忽略不计。
(1)在加速过程中,当外力做功的功率等于电阻R热功率的2倍时,金属棒的速度大小是多少
(2)如果金属棒达到(1)中的速度时断开开关S,改变外力使金属棒保持此速度做匀速运动。之后某时刻,外力做功的功率等于电阻R热功率的2倍,求此时电容器两极间的电压及从断开S开始到此刻外力做的功。
考点5 电磁感应与动量的结合
14.(多选题)(2024湖南,8)某电磁缓冲装置如图所示,两足够长的平行金属导轨置于同一水平面内,导轨左端与一阻值为R的定值电阻相连,导轨BC段与B1C1段粗糙,其余部分光滑,AA1右侧处于竖直向下的匀强磁场中,一质量为m的金属杆垂直导轨放置。现让金属杆以初速度v0沿导轨向右经过AA1进入磁场,最终恰好停在CC1处。已知金属杆接入导轨之间的阻值为R,与粗糙导轨间的动摩擦因数为μ,AB=BC=d。导轨电阻不计,重力加速度为g,下列说法正确的是( )
A.金属杆经过BB1的速度为
B.在整个过程中,定值电阻R产生的热量为m-μmgd
C.金属杆经过AA1B1B与BB1C1C区域,金属杆所受安培力的冲量相同
D.若将金属杆的初速度加倍,则金属杆在磁场中运动的距离大于原来的2倍
15.(2023全国甲,25)如图,水平桌面上固定一光滑U型金属导轨,其平行部分的间距为l,导轨的最右端与桌子右边缘对齐,导轨的电阻忽略不计。导轨所在区域有方向竖直向上的匀强磁场,磁感应强度大小为B。一质量为m、电阻为R、长度也为l的金属棒P静止在导轨上。导轨上质量为3m的绝缘棒Q位于P的左侧,以大小为v0的速度向P运动并与P发生弹性碰撞,碰撞时间极短。碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点。P在导轨上运动时,两端与导轨接触良好,P与Q始终平行。不计空气阻力。求
(1)金属棒P滑出导轨时的速度大小;
(2)金属棒P在导轨上运动过程中产生的热量;
(3)与P碰撞后,绝缘棒Q在导轨上运动的时间。
16.(2024湖北,15)如图所示,两足够长平行金属直导轨MN、PQ的间距为L,固定在同一水平面内,直导轨在左端M、P点分别与两条竖直固定、半径为L的圆弧导轨相切。M、P连线与直导轨垂直,其左侧无磁场,右侧存在磁感应强度大小为B、方向竖直向下的匀强磁场。长为L、质量为m、电阻为R的金属棒ab跨放在两圆弧导轨的最高点。质量为2m、电阻为6R的均匀金属丝制成一个半径为L的圆环,水平放置在两直导轨上,其圆心到两直导轨的距离相等。忽略导轨的电阻、所有摩擦以及金属环的可能形变,金属棒、金属环均与导轨始终接触良好,重力加速度大小为g。现将金属棒ab由静止释放,求:
(1)ab刚越过MP时产生的感应电动势大小。
(2)金属环刚开始运动时的加速度大小。
(3)为使ab在整个运动过程中不与金属环接触,金属环圆心初始位置到MP的最小距离。
高考模拟练
应用实践
1.图甲为某款“自发电”无线门铃按钮,其“发电”原理如图乙所示。按下门铃按钮过程磁铁靠近螺线管,松开门铃按钮磁铁远离螺线管回归原位置。下列说法正确的是( )
甲
乙
A.按下按钮过程,螺线管Q端电势较高
B.松开按钮过程,螺线管P端电势较低
C.按住按钮不动,螺线管中会产生感应电动势
D.按下和松开按钮过程,螺线管产生大小相同的感应电动势
2.(多选题)“电磁橇”是我国建成的世界首个电磁驱动地面超高速试验设施。图甲是一种线圈形电磁弹射装置的原理图,开关S拨向1,向电容器充电,充电完毕后,在t=0时刻开关S拨向2,发射线圈被弹射出去。图乙是驱动线圈中的电流随时间变化的图像。发射导管材质绝缘且内壁光滑。下列说法正确的是( )
甲
乙
A.开关S拨向2的瞬间,驱动线圈和发射线圈中的电流同向
B.开关S拨向2的瞬间,驱动线圈和发射线圈相互排斥
C.在0~t0时间内,发射线圈中的电流不断减小
D.发射导管越长,发射线圈的出射速度越大
3.(多选题)如图甲是游乐园常见的跳楼机,跳楼机的电磁式制动原理如图乙所示。跳楼机主干柱体上交替分布着方向相反、强弱相同的匀强磁场,每块磁场区域的宽度均为0.8 m,高度均相同,磁感应强度的大小均为1 T,中间座椅后方固定着100匝矩形线圈,线圈的宽度略大于磁场的宽度,高度与磁场高度相同,总电阻为8 Ω。若某次跳楼机由静止从高处下落,跳楼机及设备的总质量为640 kg,重力加速度g取10 m/s2,忽略摩擦阻力和空气阻力,则下列说法正确的是( )
甲
乙
A.线圈中电流方向始终为逆时针
B.跳楼机的最大速度为8 m/s
C.当跳楼机的速度为1 m/s时,线圈中感应电流为20 A
D.跳楼机速度最大时,克服安培力做功的功率为12 800 W
4.(经典题)(多选题)如图所示,一长为2l、宽为l的矩形导线框abcd,在水平外力作用下从紧靠磁感应强度为B的匀强磁场边缘处以速度v向右匀速运动3l,规定水平向左为正方向。下列关于水平外力的冲量I、导线框a、b两点间的电势差Uab、通过导线框的电荷量q及导线框所受安培力F随其运动的位移x变化的图像正确的是( )
A B
C D
5.某同学利用电压传感器来研究电感线圈工作时的特点。图甲中三个灯泡完全相同,不考虑温度对灯泡电阻的影响。在闭合开关S的同时开始采集数据,当电路达到稳定状态后断开开关。图乙是由传感器得到的电压u随时间t变化的图像。不计电源内阻及电感线圈L的直流电阻。下列说法正确的是( )
甲
乙
A.开关S闭合瞬间,流经灯D2和D3的电流相等
B.开关S闭合瞬间至断开前,流经灯D1的电流保持不变
C.开关S断开瞬间,灯D2闪亮一下再熄灭
D.根据题中信息,可以推算出图乙中u1与u2的比值
6.(经典题)(多选题)如图所示,空间存在一范围足够大的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面(竖直面)向里,MM'为磁场区域的上边界,磁场上方有一个质量为m的正方形导线框abcd,ab边与MM'平行。已知线框边长为L,总电阻为R,重力加速度为g,ab边到MM'的初始高度为H,线框从图示位置由静止开始自由下落,则( )
A.H越大时,线框进入磁场的过程中,流过横截面的电荷量越多
B.H越大时,线框刚进入磁场时的加速度越大
C.若线框出现匀速运动,其速度大小一定是
D.线框进入磁场的过程中,机械能的减少量等于克服安培力做的功
7.如图所示,两根电阻不计、足够长的平行光滑金属导轨MN、PQ固定在水平面内,间距d=1 m,在导轨间宽度L=1 m的矩形区域内有垂直于导轨平面向上的匀强磁场,磁感应强度大小B=0.5 T,一根质量mb=0.2 kg、电阻R=0.5 Ω的金属棒b静止在导轨上,现使另一根质量ma=0.1 kg、电阻也为R=0.5 Ω的金属棒a以初速度v0=4 m/s从左端开始沿导轨滑动,穿过磁场区域后,与b发生弹性碰撞,两金属棒始终与导轨垂直且接触良好。求:
(1)金属棒a在第一次穿越磁场的过程中回路中感应电流的方向(从上向下看,是顺时针还是逆时针,写出结果即可);
(2)金属棒a在第一次穿越磁场的过程中流过金属棒a的电荷量q;
(3)金属棒a穿出磁场时的速度大小v1;
(4)在与金属棒b碰撞后,金属棒a的速度v2。
8.如图甲所示,足够长的光滑平行金属导轨JK、PQ倾斜放置,两导轨间距为L=1.0 m,导轨平面与水平面间的夹角为θ=30°,磁感应强度为B的匀强磁场垂直于导轨平面向上(图中未画出),导轨的J、P两端连接阻值为R=3.0 Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.90 kg,电阻r=0.50 Ω,重物的质量M=1.50 kg,如果将金属棒和重物由静止释放,金属棒沿导轨上滑的距离与时间的关系图像如图乙所示,不计导轨电阻,重力加速度g=10 m/s2。求:
(1)t=0时刻金属棒ab的加速度大小;
(2)求磁感应强度B的大小以及在1.2 s内通过电阻R的电荷量;
(3)在1.2 s内电阻R产生的热量。
甲
乙
迁移创新
9.一种可测速的跑步机的测速原理如图所示。该机底面固定有间距为L、宽度为d的平行金属电极。电极间充满磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,左侧接有电压表和电阻R。绝缘橡胶带上每隔距离d就嵌入一个电阻为r的平行细金属条,跑步过程中,绝缘橡胶带跟随脚步一起运动,金属条和电极之间接触良好且任意时刻仅有一根金属条处于磁场中。现在测出t时间内电压表读数恒为U,设人与跑步机间无相对滑动。
(1)判断电阻R中的电流方向。
(2)人跑步过程中,是否匀速 给出判断的理由。
(3)求t时间内人的平均跑步速度大小。
(4)若跑步过程中,人体消耗的能量有20%用于克服磁场力做功,求t时间内人体消耗的能量。
答案与分层梯度式解析
高考真题练
1.D 2.ABD 3.A 4.C 5.AD 6.A
7.AC 8.AD 9.D 10.AB 11.C 14.CD
1.D 题图乙所示情况下,穿过线圈的磁通量为0,A错误;由法拉第电磁感应定律可知,永磁铁相对线圈上升越快,磁通量变化越快,线圈中的感应电动势越大,永磁铁相对线圈上升越高时速度越小(点拨:永磁铁是上下振动的运动形式,故永磁铁相对线圈上升或下降的距离越大,速度越小),B、C错误;永磁铁相对线圈下降,穿过线圈的磁通量向外增大,由楞次定律结合安培定则可知,线圈中感应电流的方向为顺时针方向,D正确。
2.ABD MN最终受到重力和导轨的支持力保持静止,则一定静止于最低点OO'位置,A正确;根据楞次定律可知,MN运动过程中安培力始终做负功,B正确;从释放到第一次到达OO'位置的过程中,MN的速率先增大后减小,C错误;从释放到第一次到达OO'位置的过程中,根据右手定则可知MN中电流方向由M到N,D正确。
3.A 根据法拉第电磁感应定律可知,平均感应电动势E==,故A正确。
4.C
关键点拨 导体切割磁感线的有效长度是导体在垂直速度方向上的投影长度。
选取Oa直线段,由右手定则容易判断O点的电势高于a点的电势,排除B、D选项;A、C选项的主要区别是对b、c两点电势高低的判断,如图所示,导线Oab的等效长度为Ob,导线Oabc的等效长度为Oc,由几何关系可知Ob=Oc,b、c处的线速度大小相等,则UOb=UOc,故b、c两点的电势相等,C正确,A错误。
5.AD 杆OP匀速转动,由E=Bl2ω可知杆OP产生的感应电动势恒定,选项A正确;由右手定则可知,杆OP产生了由O到P的感应电流,则由左手定则可知MN会受到向左的安培力,在MN向左运动的过程中,由右手定则可判定MN切割磁感线产生由N到M的感应电动势,则通过MN的电流逐渐减小,由安培力F=BIl可知,杆MN、杆OP所受的安培力减小,杆MN做加速度减小的加速运动,故选项B、C错误,D正确。
6.A 金属棒切割磁感线产生的电动势E=BLv=2Bxv tan θ,电容器极板上的电荷量Q=CU=CE=2CBxv tan θ,通过金属棒的电流I===2BCv2 tan θ,选项A正确。金属棒到达x0时,Q=2BCx0v tan θ,B错误。根据右手定则,可知金属棒中电流从下向上流,上极板带正电,C错误。外力F=F安,F安=IBL,P=Fv=4B2Cv3x tan2 θ,则随着x的增加,P增加,D错误。
7.AC 设ab、cd导轨与x轴夹角为θ,过原点O时,金属棒有效长度为y0,则在0~ 时间内,金属棒切割磁感线的有效长度为y=y0+v0t tan θ,则产生的感应电动势E=Byv0=By0v0+Bt tan θ,感应电动势E与t是一次函数关系,则感应电流i与时间t是一次函数关系,在~时间内,金属棒切割磁感线的有效长度不变,所以感应电动势不变,感应电流不变,在~时间内相当于0~时间内的逆过程,因此选项A正确;由于不计电阻R之外的所有电阻,所以电阻R两端电压与感应电动势相等,选项D错误;当t=0、t=时,金属棒产生的感应电动势并不等于零,电流也不等于零,所以安培力并不等于0,选项B错误;在0~时间内,金属棒克服安培力做功的功率P=Fv0==(y0+v0t tan θ)2,P-t图线是抛物线的一部分,在~时间内切割磁感线有效长度不变,P=Fv0=,所以P恒定,在~时间内相当于0~时间内的逆过程,选项C正确。
8.AD 合上开关的瞬间,导体棒两端电压等于电容器两端电压且为最大值,电流也最大,I==,电流最大时,导体棒MN所受的安培力最大,而导体棒速度最大时电流不是最大,所以A正确,C错误;导体棒MN先加速后减速,不会匀速,如果导体棒MN做匀速直线运动,电阻上一直有焦耳热产生,其他能量都不变,不符合能量守恒定律,所以B错误;由于棒运动过程切割磁感线产生反电动势,导致只有开始时通过电阻R的电流与通过导体棒MN的电流相等,其他时候通过电阻R的电流都比通过导体棒MN的电流大,故由焦耳定律可知电阻R上产生的焦耳热比导体棒MN上产生的焦耳热多,D正确。
易混易错 导体棒加速时通过其电流由M到N,减速时电流由N到M。
9.D 根据右手定则可知,流过杆的感应电流方向为从M到N,A错误;由于杆在磁场中运动时会受到沿导轨向上的安培力,加速度逐渐减小,所以≠=v,则杆沿导轨下滑的距离不等于vt,故B错误;由于杆沿导轨下滑过程中只有安培力和重力做功,最终导体杆的速度增加,说明合外力做正功,也就是说运动过程中导体杆克服安培力做的功小于重力做的功,所以流过杆感应电流的平均电功率小于重力的平均功率,C错误;以沿导轨向下为正方向,根据动量定理可得mgt sin θ-I安=2mv-mv,解得杆所受安培力的冲量I安=mgt sin θ-mv,D正确。
10.AB 由右手定则可知回路中的电流方向为abcda,故A正确;导轨倾角θ=30°,ab棒稳定时有2mg· tan θ=F安=2BIL,得I==,B正确;加速时,对ab棒有2mg·sin θ-2BLI cos θ=2ma1,对cd棒有mg·sin θ-BLI cos θ=ma2,解得a1=a2=g sin θ-,加速度大小的表达式相同,C错误;由法拉第电磁感应定律可知E感=BLv cos θ,v、L、θ相同,但B不同,所以两棒产生的电动势不相等,D错误。
11.C 开关接1,导体棒处于静止状态时,其受力分析如图,可知tan =,而I=,解得E0=,选项A错误;
开关接2,导体棒从题图所示位置向左运动到左侧最高点过程中,根据右手定则可知,电流垂直纸面向里,即有电流通过二极管,则有安培力阻碍导体棒向左摆动,故棒在左侧的最大摆角小于,从左向右摆动过程中,根据右手定则可知二极管截止,没有电流经过,即没有安培力阻碍导体棒运动,最大摆角与左侧最大摆角相同,选项C正确;根据能量守恒定律可知,从右向左经过最低点的速度要大于从左向右经过最低点的速度,因此感应电动势并不等大,选项D错误;由于不知道棒运动到最左侧时的高度,所以无法计算棒消耗的焦耳热,选项B错误。
12.答案 (1) (2)- tan θ
解析 (1)感应电动势最大值Emax=Bω=BL2ω
感应电流最大值Imax=
CD棒所受安培力的最大值Fmax=BImaxL
解得Fmax=
感应电动势最小值Emin=BL2ω
感应电流最小值Imin=
CD棒所受安培力的最小值Fmin=BIminL=
(2)由题意知Fmax=mg sin θ+fm
Fmin=mg sin θ-fm
联立解得m=
CD棒沿导轨下滑,所受滑动摩擦力沿导轨向上,撤去推力瞬间,所受安培力大小等于(1)问中安培力的最大值,则CD棒的加速度方向沿导轨向上。
根据牛顿第二定律,Fmax+μmg cos θ-mg sin θ=ma
解得μ=- tan θ
方法技巧
导体转动切割磁感线产生感应电动势的求法
若长为L的导体棒在磁感应强度为B的匀强磁场中以角速度ω匀速转动,则
(1)以中点为轴时,E=0(不同两段的电动势的代数和为零)。
(2)以端点为轴时E=BωL2(平均速度取中点位置的线速度ωL)。
(3)以任意点为轴时E=Bω(-)(L1>L2,不同两段的电动势的代数和)。
13.答案 (1) (2)
解析 (1)设金属棒的速度为v,则感应电动势为E=Blv
感应电流为I==
金属棒所受的安培力为F安=BIl=
金属棒以速率v0匀速运动时,外力为F=F安1=
外力的功率为PF=Fv=
电阻R的热功率为PR=I2R=
依题意有:PF=2PR
解得v=
(2)金属棒相当于电源,电动势为E'=
设此时电容器的电压为UC,则电阻R的电压为UR=E'-UC
电阻R中的电流为I'=(点拨:电容器的部分为非纯电阻电路,只能通过电阻R应用欧姆定律求解电路的电流)
电阻R的热功率为PR'=URI'=
外力的功率即电源的功率,为
PF'=E'I'=
由题意有:PF'=2PR'
解得:UC==
电容器的电荷量为Q=CUC=
通过电源的电荷量也为Q,由电动势的定义得这段时间内非静电力做的功为W=QE'
解得W=
所以从断开S开始到此刻外力做的功为
归纳总结 (1)“匀速”→此时的安培力等于恒定外力。
(2)金属棒相当于电源,只有电阻R能应用欧姆定律,电容器的部分是非纯电阻电路。
(3)第(2)问中所涉及的是给电容器充电的过程,电路中的电流是变化的,但电源的电动势恒定不变。
(4)外力是变力,要应用W=qU进行巧妙的等效转化,简便地求出变力的功。
14.CD 金属杆通过光滑导轨时,根据动量定理得-BL·t1=mv-mv0,其中·t1=q1=;同理,金属杆通过粗糙导轨时,根据动量定理得-BL·t2-μmg·t2=0-mv,其中·t2=q2=,由此可知mv>mv0-mv,则金属杆经过BB1的速度v>,A错误;
根据能量守恒可知,整个回路中产生的总热量Q=m-μmgd,则定值电阻R上产生的热量QR==m-μmgd,B错误;金属杆所受安培力的冲量I=BL·t=BLq,而q=,所以金属杆经过AA1B1B与BB1C1C区域,安培力的冲量相同,C正确;由A项分析知--μmgt2=0-mv0,若将金属杆的初速度加倍,设金属杆在磁场中运动的距离为x,由动量定理知--μmgt3=0-m·2v0,由于t3μmg·t3,则x>4d,即大于原来的2倍,D正确。
15.答案 (1) (2)m (3)
关键点拨 (1)注意Q棒是绝缘棒,不会有电流通过Q棒,且导轨光滑,说明Q棒与P棒碰撞前后Q棒均做匀速直线运动。
(2)P棒与Q棒滑出导轨后落在地面上同一点,说明P棒与Q棒滑出导轨时的速度相同。
(3)第(3)问求的是绝缘棒Q与金属棒P碰撞后在导轨上做匀速直线运动的时间。
解析 (1)由于绝缘棒Q与金属棒P的碰撞为弹性碰撞,金属导轨光滑,可知Q棒与P棒组成的系统动量守恒,机械能守恒,有3mv0=3mv'1+mv'2①
×3m=×3mv1'2+mv2'2②
联立①②得v'1=,v'2=v0
绝缘棒Q在水平方向所受合力为0,碰后做匀速直线运动,而P、Q落在地面同一点,可知P棒滑出导轨时的速度等于Q棒滑出导轨时的速度,即金属棒P滑出导轨时的速度大小为。
(2)由能量守恒定律可知,金属棒P减少的动能转化为运动过程中P棒产生的焦耳热,有
QP=mv2'2-mv1'2=m×-m×=m③
(3)对P棒回路由法拉第电磁感应定律有
=n (其中n=1)④
=⑤
q=·Δt⑥
联立④⑤⑥得q==⑦
可知碰撞后P的位移为
x=⑧
对P棒应用动量定理有
-BlΔt=mΔv⑨
整理有-Blq=mv'1-mv'2=-mv0
解得q=⑩
从Q与P碰撞到Q滑出导轨,Q与P在导轨上运动的位移相同,都是x,Q做匀速直线运动,则与P碰撞后,设绝缘棒Q在导轨上运动的时间为t'
t'=
联立①②⑧⑩可得t'=
16.答案 (1)BL (2)
(3)
解析 (1)设ab棒刚到MP处时的速度为v0,
由动能定理得mgL=m①
产生的电动势E0=BLv0②
由①②式得E0=BL
(2)将圆环分成4段,如图所示:由几何关系可知Rcf=R,Rde=R
由于导轨电阻不计,可认为cd、ef段被短路,圆环等效电阻R'==③
金属环中总电流I0=④
安培力大小F0=BI1L+BI2L=BI0L⑤
由牛顿第二定律有F0=2ma0⑥
由①~⑥式得a0=
(3)当棒ab的速度v1大于圆环速度v2时回路会有感应电流,安培力使ab减速,使圆环加速,直到ab速度等于圆环速度,此后圆环与棒ab一起匀速运动。设共同速度为vt,极短时间Δt内,由动量定理
对棒有BIL·Δt=mΔv1
对圆环BIL·Δt=2mΔv2
求和ΣBIL·Δt=Σm·Δv1
可得BLq=m(v0-vt)⑦
ΣBILΔt=Σ2mΔv2
可得BLq=2m·vt⑧
由⑦⑧式得
由闭合电路欧姆定律可得E1-E2=I·(R+R')
BLv1-BLv2=IR
BLv1Δt-BLv2Δt=IΔt·R
ΣBLv1Δt-ΣBLv2Δt=RΣIΔt
BLΣ(v1Δt-v2Δt)=RΣIΔt
BLΔx=Rq
Δx===
最小距离s=L+Δx=L+=
高考模拟练
1.A 2.BC 3.CD 4.AB 5.D 6.CD
1.A 按下按钮过程,穿过螺线管的磁通量向左且增大,根据楞次定律结合安培定则可知螺线管中感应电流为从P端流入从Q端流出,螺线管充当电源,则Q端电势较高;同理可知,松开按钮过程,P端电势较高,故A正确,B错误;按住按钮不动,穿过螺线管的磁通量不变,螺线管不会产生感应电动势,C错误;按下和松开按钮过程,螺线管中磁通量的变化率不一定相同,故螺线管产生的感应电动势不一定相同,D错误。
2.BC 开关S拨向2的瞬间,驱动线圈中的电流增大,线圈周围的磁场增强,根据楞次定律,发射线圈中的感应电流与驱动线圈中的电流反向,驱动线圈和发射线圈相互排斥,A错误,B正确;0~t0时间内,驱动线圈中的电流变化率逐渐减小,则周围磁感应强度的变化率逐渐减小,由法拉第电磁感应定律,发射线圈中的感应电动势减小,发射线圈中的电流不断减小,C正确;t0时刻后驱动线圈中电流减小,发射线圈中的感应电流与驱动线圈中的电流同向,驱动线圈和发射线圈相互吸引,发射线圈减速,只有选择合适的发射导管,使发射线圈在t0时刻能刚好到达管口,发射线圈的出射速度才最大,D错误。
方法技巧
根据图像分析问题的三个关键点
(1)弄清图像所揭示的物理规律或物理量间的函数关系。
(2)挖掘图像中的隐含条件,明确有关图线所包围的面积、图线的斜率(或其绝对值)、截距所表示的物理意义。
(3)借助有关的物理概念、公式、定理和定律做出分析判断。
3.CD 由右手定则可知,线圈中的电流方向为逆时针与顺时针交替变化,故A错误。跳楼机由静止下落后受安培力与重力,根据牛顿第二定律有mg-F安=ma,且安培力F安=2nBIL,E=2nBLv,I=,联立可得mg-=ma;随着速度的增大,加速度减小,当加速度为0时,速度达到最大值,以后跳楼机做匀速运动;当跳楼机速度最大时,安培力与重力平衡,有mg=F安m=,解得vm=2 m/s,此时克服安培力做功的功率为P安=F安m·vm=mgvm=640×10×2 W=12 800 W,故B错误,D正确。当跳楼机的速度为1 m/s时,线圈中的感应电流为I=== A=20 A,C正确。
4.AB 由于导线框做匀速运动,可知水平外力和安培力F大小相等,方向相反。导线框进入磁场的过程中,安培力为F=BIl=,B、l、v不变,则F不变,水平外力的冲量I=-Ft=-;完全进入磁场后,感应电流为零,安培力为零,故外力为零,冲量不变,A正确,D错误。进入磁场的过程中,有Uab=RI电=Blv,完全进入磁场后,a、b两点间的电势差为Uab=Blv,B正确;进入磁场的过程中,q=Δt==,完全进入磁场后感应电流为零,q不变,但不为零,C错误。
5.D 开关S闭合瞬间,D2立即发光,由于电感线圈L的自感,阻碍电流的增大,流经灯D3的电流小于流经D2的电流,A错误。开关闭合瞬间,电路等效于灯D1和D2串联,待稳定后,灯D2和D3并联后再与灯D1串联,总电阻比开关闭合瞬间小,故从开关S闭合瞬间至断开前,流经灯D1的电流是变化的,B错误。开关S断开前,流经灯D2和D3的电流相等,开关S断开瞬间,线圈L产生自感电动势阻碍电流的减小,由线圈L为灯D2和D3供电,流经灯D2的电流并没有突然增大,D2不会闪亮,只是逐渐熄灭,C错误。开关S闭合瞬间,电压传感器所在支路相当于断路,电路等效于灯D1和D2串联,电压传感器所测电压为D2两端电压,由串联分压规律可知u1=;电路稳定后,由欧姆定律可知流过D3的电流为I=·=;开关S断开瞬间,电感线圈L能够为D2和D3提供与之前等大的电流,其两端电压为u2=I·2R=,所以=,故可以推算出题图乙中u1与u2的比值,D正确。
6.CD 线框进入磁场过程中,平均感应电动势为=,平均感应电流为=,则线框进入磁场的过程中,流过横截面的电荷量为q=Δt==,可知流过横截面的电荷量与下落高度无关,故A错误。根据题意可知,ab边进入磁场前线框做自由落体运动,由v2=2gh可得,线框刚进入磁场时的速度为v=,产生的感应电动势为E=BLv,感应电流为I=,安培力为F=BIL=,由右手定则和左手定则可知,安培力竖直向上;若线框匀速运动,则有=mg,联立解得v=,H=;可知,若H>,则线框进入磁场时,安培力大于重力,由牛顿第二定律有-mg=ma,可知H越大,进入磁场时的加速度越大;若H<,则线框进入磁场时,安培力小于重力,由牛顿第二定律有mg-=ma,可知H越大,进入磁场时的加速度越小,故B错误,C正确。线框进入磁场的过程中,除了重力之外只有安培力做功,由功能关系可知,机械能的减少量等于克服安培力做的功,故D正确。
7.答案 (1)逆时针 (2)0.5 C (3)1.5 m/s
(4)0.5 m/s,方向向左
解析 (1)由右手定则可知,金属棒a第一次穿越磁场时回路中有逆时针方向的感应电流。
(2)金属棒a在第一次穿越磁场的过程中,平均感应电动势=,通过金属棒a的电荷量q=·Δt=·Δt=== C=0.5 C。
(3)金属棒a第一次穿越磁场的过程中,由动量定理可得
-BdΔt=mav1-mav0
q=·Δt=0.5 C
代入数据解得v1=1.5 m/s。
(4)两棒发生弹性碰撞,以向右为正方向,由动量守恒定律有mav1=mav2+mbv
由机械能守恒由ma=ma+mbv2
代入解得v2=-0.5 m/s,负号表示速度方向向左。
8.答案 (1)4.375 m/s2 (2) T C
(3)9.45 J
解析 (1)以金属棒ab和重物整体为研究对象,t=0时刻,根据牛顿第二定律得
Mg-mg sin θ=(M+m)a
解得a=4.375 m/s2。
(2)由题图乙可以看出,最终金属棒ab将匀速运动,匀速运动的速度为v== m/s=1.75 m/s
此时金属棒ab切割磁感线产生的感应电动势E=BLv
感应电流 I=
金属棒ab所受的安培力 F=BIL=
金属棒ab匀速运动时,金属棒和重物整体受力平衡,可得 F+mg sin θ=Mg
联立解得B= T
在1.2 s内通过电阻R的电荷量 q=== C。
(3)对金属棒和重物整体,由能量守恒定律得Mgs=mgs sin θ+Q+(M+m)v2
且有 QR=Q
联立解得QR=9.45 J。
方法技巧 电荷量、磁通量的变化量、安培力的冲量间的关系
设想在某一回路中,一金属杆运动时,感应电流在改变,安培力F为变力。
设在Δt时间内的平均电流为,平均感应电动势为,则=,==,
Δt时间内通过金属杆的电荷量q=Δt=;
设在Δt时间内的平均安培力为,平均电流为,安培力的冲量为I=Δt=BLΔt,
通过金属杆的电荷量q=Δt=。
9.答案 (1)向下 (2)见解析 (3)U
(4)
解析 (1)由题意根据右手定则可知,电阻R中的电流方向向下。
(2)(3)金属条做切割磁感线运动产生的感应电动势大小为E=BLv,
回路中的电流大小为I=,
电压表的示数为U=IR,
解得v=U,
由于电压表示数恒定,所以金属条的运动速度也恒定,说明人跑步过程中是匀速的。
人的平均跑步速度大小等于金属条的运动速度,为
v'=U。
(4)金属条中的电流为I=,
金属条受到的安培力大小为FA=ILB,
t时间内金属条克服安培力做的功为
W=FAvt==,
所以t时间内人体消耗的能量
E==。
方法创新 本题属于理论联系实际问题,关键是建立物理模型——“单杆模型”,人跑动时带动绝缘橡胶带上固定的细金属条运动,当细金属条在磁场中运动时切割磁感线,产生感应电动势,给电阻供电,通过电压表可读出路端电压,然后分析各个问题。
10
高考真题练
考点1 安培定则、楞次定律的综合应用
1.(2024广东,4)电磁俘能器可在汽车发动机振动时利用电磁感应发电实现能量回收,结构如图甲所示。两对永磁铁可随发动机一起上下振动,每对永磁铁间有水平方向的匀强磁场,磁感应强度大小均为B。磁场中,边长为L的正方形线圈竖直固定在减震装置上。某时刻磁场分布与线圈位置如图乙所示,永磁铁振动时磁场分界线不会离开线圈。关于图乙中的线圈,下列说法正确的是( )
A.穿过线圈的磁通量为BL2
B.永磁铁相对线圈上升越高,线圈中感应电动势越大
C.永磁铁相对线圈上升越快,线圈中感应电动势越小
D.永磁铁相对线圈下降时,线圈中感应电流的方向为顺时针方向
2.(多选题)(2024山东,11)如图所示,两条相同的半圆弧形光滑金属导轨固定在水平桌面上,其所在平面竖直且平行,导轨最高点到水平桌面的距离等于半径,最低点的连线OO'与导轨所在竖直面垂直。空间充满竖直向下的匀强磁场(图中未画出),导轨左端由导线连接。现将具有一定质量和电阻的金属棒MN平行OO'放置在导轨图示位置,由静止释放。MN运动过程中始终平行于OO'且与两导轨接触良好,不考虑自感影响,下列说法正确的是( )
A.MN最终一定静止于OO'位置
B.MN运动过程中安培力始终做负功
C.从释放到第一次到达OO'位置过程中,MN的速率一直在增大
D.从释放到第一次到达OO'位置过程中,MN中电流方向由M到N
考点2 法拉第电磁感应定律的简单应用
3.(2023重庆,2)某小组设计了一种呼吸监测方案:在人身上缠绕弹性金属线圈,观察人呼吸时处于匀强磁场中的线圈面积变化产生的电压,了解人的呼吸状况。如图所示,线圈P的匝数为N,磁场的磁感应强度大小为B,方向与线圈轴线的夹角为θ。若某次吸气时,在t时间内每匝线圈面积增加了S,则线圈P在该时间内的平均感应电动势为( )
A. B.
C. D.
4.(2024湖南,4)如图,有一硬质导线Oabc,其中是半径为R的半圆弧,b为圆弧的中点,直线段Oa长为R且垂直于直径ac。该导线在纸面内绕O点逆时针转动,导线始终在垂直纸面向里的匀强磁场中。则O、a、b、c各点电势关系为( )
A.φO>φa>φb>φc B.φO<φa<φb<φc
C.φO>φa>φb=φc D.φO<φa<φb=φc
5.(多选题)(2021广东,10)如图所示,水平放置足够长光滑金属导轨abc和de,ab与de平行,bc是以O为圆心的圆弧导轨。圆弧be左侧和扇形Obc内有方向如图的匀强磁场。金属杆OP的O端与e点用导线相接,P端与圆弧bc接触良好。初始时,可滑动的金属杆MN静止在平行导轨上。若杆OP绕O点在匀强磁场区内从b到c匀速转动时,回路中始终有电流,则此过程中,下列说法正确的有( )
A.杆OP产生的感应电动势恒定
B.杆OP受到的安培力不变
C.杆MN做匀加速直线运动
D.杆MN中的电流逐渐减小
6.(2021河北,7)如图,两光滑导轨水平放置在竖直向下的匀强磁场中,磁感应强度大小为B。导轨间距最窄处为一狭缝,取狭缝所在处O点为坐标原点。狭缝右侧两导轨与x轴夹角均为θ,一电容为C的电容器与导轨左端相连。导轨上的金属棒与x轴垂直,在外力F作用下从O点开始以速度v向右做匀速运动,忽略所有电阻。下列说法正确的是( )
A.通过金属棒的电流为2BCv2 tan θ
B.金属棒到达x0时,电容器极板上的电荷量为BCvx0 tan θ
C.金属棒运动过程中,电容器的上极板带负电
D.金属棒运动过程中,外力F做功的功率恒定
考点3 电磁感应中的图像问题
7.(多选题)(2022河北,8)如图,两光滑导轨水平放置在竖直向下的匀强磁场中,一根导轨位于x轴上,另一根由ab、bc、cd三段直导轨组成,其中bc段与x轴平行,导轨左端接入一电阻R。导轨上一金属棒MN沿x轴
正方向以速度v0保持匀速运动,t=0时刻通过坐标原点O,金属棒始终与x轴垂直。设运动过程中通过电阻的电流强度为i,金属棒受到安培力的大小为F,金属棒克服安培力做功的功率为P,电阻两端的电压为U。导轨与金属棒接触良好,忽略导轨与金属棒的电阻。下列图像可能正确的是( )
A B
C D
考点4 电磁感应中的动力学与能量问题
8.(多选题)(2022全国甲,20)如图,两根相互平行的光滑长直金属导轨固定在水平绝缘桌面上,在导轨的左端接入电容为C的电容器和阻值为R的电阻。质量为m、阻值也为R的导体棒MN静止于导轨上,与导轨垂直,且接触良好,导轨电阻忽略不计,整个系统处于方向竖直向下的匀强磁场中。开始时,电容器所带的电荷量为Q,合上开关S后,( )
A.通过导体棒MN电流的最大值为
B.导体棒MN向右先加速、后匀速运动
C.导体棒MN速度最大时所受的安培力也最大
D.电阻R上产生的焦耳热大于导体棒MN上产生的焦耳热
9.(2023重庆,7)如图所示,与水平面夹角为θ的绝缘斜面上固定有光滑U形金属导轨。质量为m、电阻不可忽略的导体杆MN沿导轨向下运动,以大小为v的速度进入方向垂直于导轨平面向下的匀强磁场区域,在磁场中运动一段时间t后,速度大小变为2v。运动过程中杆与导轨垂直并接触良好,导轨的电阻忽略不计,重力加速度为g。杆在磁场中运动的此段时间内( )
A.流过杆的感应电流方向从N到M
B.杆沿轨道下滑的距离为vt
C.流过杆感应电流的平均电功率等于重力的平均功率
D.杆所受安培力的冲量大小为mgt sin θ-mv
10.(多选题)(2024黑吉辽,9)如图,两条“∧”形的光滑平行金属导轨固定在绝缘水平面上,间距为L,左、右两导轨面与水平面夹角均为30°,均处于竖直向上的匀强磁场中,磁感应强度大小分别为2B和B。将有一定阻值的导体棒ab、cd放置在导轨上,同时由静止释放,两棒在下滑过程中始终与导轨垂直并接触良好。ab、cd的质量分别为2m和m,长度均为L。导轨足够长且电阻不计,重力加速度大小为g。两棒在下滑过程中( )
A.回路中的电流方向为abcda
B.ab中电流趋于
C.ab与cd加速度大小之比始终为2∶1
D.两棒产生的电动势始终相等
11.(2023浙江6月选考,10)如图所示,质量为M、电阻为R、长为L的导体棒,通过两根长均为l、质量不计的导电细杆连在等高的两固定点上,固定点间距也为L。细杆通过开关S可与直流电源E0或理想二极管串接。在导体棒所在空间存在磁感应强度方向竖直向上、大小为B的匀强磁场,不计空气阻力和其他电阻。开关S接1,当导体棒静止时,细杆与竖直方向的夹角θ=,重力加速度为g;然后开关S接2,棒从右侧开始运动完成一次振动的过程中( )
A.电源电动势E0=R
B.棒消耗的焦耳热Q=Mgl
C.从左向右运动时,最大摆角小于
D.棒两次过最低点时感应电动势大小相等
12.(2024河北,14)如图,边长为2L的正方形金属细框固定放置在绝缘水平面上,细框中心O处固定一竖直细导体轴OO'。间距为L、与水平面成θ角的平行导轨通过导线分别与细框及导体轴相连。导轨和细框分别处在与各自所在平面垂直的匀强磁场中,磁感应强度大小均为B。足够长的细导体棒OA在水平面内绕O点以角速度ω匀速转动,水平放置在导轨上的导体棒CD始终静止。OA棒在转动过程中,CD棒在所受安培力达到最大和最小时均恰好能静止。已知CD棒在导轨间的电阻值为R,电路中其余部分的电阻均不计,CD棒始终与导轨垂直,各部分始终接触良好,不计空气阻力,重力加速度大小为g。
(1)求CD棒所受安培力的最大值和最小值。
(2)锁定OA棒,推动CD棒下滑,撤去推力瞬间,CD棒的加速度大小为a,所受安培力大小等于(1)问中安培力的最大值,求CD棒与导轨间的动摩擦因数。
13.(2024全国甲,25)两根平行长直光滑金属导轨距离为l,固定在同一水平面(纸面)内,导轨左端接有电容为C的电容器和阻值为R的电阻,开关S与电容器并联;导轨上有一长度略大于l的金属棒,如图所示。导轨所处区域有方向垂直于纸面、磁感应强度大小为B的匀强磁场。开关S闭合。金属棒在恒定的外力作用下由静止开始加速,最后将做速率为v0的匀速直线运动。金属棒始终与两导轨垂直且接触良好,导轨电阻和金属棒电阻忽略不计。
(1)在加速过程中,当外力做功的功率等于电阻R热功率的2倍时,金属棒的速度大小是多少
(2)如果金属棒达到(1)中的速度时断开开关S,改变外力使金属棒保持此速度做匀速运动。之后某时刻,外力做功的功率等于电阻R热功率的2倍,求此时电容器两极间的电压及从断开S开始到此刻外力做的功。
考点5 电磁感应与动量的结合
14.(多选题)(2024湖南,8)某电磁缓冲装置如图所示,两足够长的平行金属导轨置于同一水平面内,导轨左端与一阻值为R的定值电阻相连,导轨BC段与B1C1段粗糙,其余部分光滑,AA1右侧处于竖直向下的匀强磁场中,一质量为m的金属杆垂直导轨放置。现让金属杆以初速度v0沿导轨向右经过AA1进入磁场,最终恰好停在CC1处。已知金属杆接入导轨之间的阻值为R,与粗糙导轨间的动摩擦因数为μ,AB=BC=d。导轨电阻不计,重力加速度为g,下列说法正确的是( )
A.金属杆经过BB1的速度为
B.在整个过程中,定值电阻R产生的热量为m-μmgd
C.金属杆经过AA1B1B与BB1C1C区域,金属杆所受安培力的冲量相同
D.若将金属杆的初速度加倍,则金属杆在磁场中运动的距离大于原来的2倍
15.(2023全国甲,25)如图,水平桌面上固定一光滑U型金属导轨,其平行部分的间距为l,导轨的最右端与桌子右边缘对齐,导轨的电阻忽略不计。导轨所在区域有方向竖直向上的匀强磁场,磁感应强度大小为B。一质量为m、电阻为R、长度也为l的金属棒P静止在导轨上。导轨上质量为3m的绝缘棒Q位于P的左侧,以大小为v0的速度向P运动并与P发生弹性碰撞,碰撞时间极短。碰撞一次后,P和Q先后从导轨的最右端滑出导轨,并落在地面上同一地点。P在导轨上运动时,两端与导轨接触良好,P与Q始终平行。不计空气阻力。求
(1)金属棒P滑出导轨时的速度大小;
(2)金属棒P在导轨上运动过程中产生的热量;
(3)与P碰撞后,绝缘棒Q在导轨上运动的时间。
16.(2024湖北,15)如图所示,两足够长平行金属直导轨MN、PQ的间距为L,固定在同一水平面内,直导轨在左端M、P点分别与两条竖直固定、半径为L的圆弧导轨相切。M、P连线与直导轨垂直,其左侧无磁场,右侧存在磁感应强度大小为B、方向竖直向下的匀强磁场。长为L、质量为m、电阻为R的金属棒ab跨放在两圆弧导轨的最高点。质量为2m、电阻为6R的均匀金属丝制成一个半径为L的圆环,水平放置在两直导轨上,其圆心到两直导轨的距离相等。忽略导轨的电阻、所有摩擦以及金属环的可能形变,金属棒、金属环均与导轨始终接触良好,重力加速度大小为g。现将金属棒ab由静止释放,求:
(1)ab刚越过MP时产生的感应电动势大小。
(2)金属环刚开始运动时的加速度大小。
(3)为使ab在整个运动过程中不与金属环接触,金属环圆心初始位置到MP的最小距离。
高考模拟练
应用实践
1.图甲为某款“自发电”无线门铃按钮,其“发电”原理如图乙所示。按下门铃按钮过程磁铁靠近螺线管,松开门铃按钮磁铁远离螺线管回归原位置。下列说法正确的是( )
甲
乙
A.按下按钮过程,螺线管Q端电势较高
B.松开按钮过程,螺线管P端电势较低
C.按住按钮不动,螺线管中会产生感应电动势
D.按下和松开按钮过程,螺线管产生大小相同的感应电动势
2.(多选题)“电磁橇”是我国建成的世界首个电磁驱动地面超高速试验设施。图甲是一种线圈形电磁弹射装置的原理图,开关S拨向1,向电容器充电,充电完毕后,在t=0时刻开关S拨向2,发射线圈被弹射出去。图乙是驱动线圈中的电流随时间变化的图像。发射导管材质绝缘且内壁光滑。下列说法正确的是( )
甲
乙
A.开关S拨向2的瞬间,驱动线圈和发射线圈中的电流同向
B.开关S拨向2的瞬间,驱动线圈和发射线圈相互排斥
C.在0~t0时间内,发射线圈中的电流不断减小
D.发射导管越长,发射线圈的出射速度越大
3.(多选题)如图甲是游乐园常见的跳楼机,跳楼机的电磁式制动原理如图乙所示。跳楼机主干柱体上交替分布着方向相反、强弱相同的匀强磁场,每块磁场区域的宽度均为0.8 m,高度均相同,磁感应强度的大小均为1 T,中间座椅后方固定着100匝矩形线圈,线圈的宽度略大于磁场的宽度,高度与磁场高度相同,总电阻为8 Ω。若某次跳楼机由静止从高处下落,跳楼机及设备的总质量为640 kg,重力加速度g取10 m/s2,忽略摩擦阻力和空气阻力,则下列说法正确的是( )
甲
乙
A.线圈中电流方向始终为逆时针
B.跳楼机的最大速度为8 m/s
C.当跳楼机的速度为1 m/s时,线圈中感应电流为20 A
D.跳楼机速度最大时,克服安培力做功的功率为12 800 W
4.(经典题)(多选题)如图所示,一长为2l、宽为l的矩形导线框abcd,在水平外力作用下从紧靠磁感应强度为B的匀强磁场边缘处以速度v向右匀速运动3l,规定水平向左为正方向。下列关于水平外力的冲量I、导线框a、b两点间的电势差Uab、通过导线框的电荷量q及导线框所受安培力F随其运动的位移x变化的图像正确的是( )
A B
C D
5.某同学利用电压传感器来研究电感线圈工作时的特点。图甲中三个灯泡完全相同,不考虑温度对灯泡电阻的影响。在闭合开关S的同时开始采集数据,当电路达到稳定状态后断开开关。图乙是由传感器得到的电压u随时间t变化的图像。不计电源内阻及电感线圈L的直流电阻。下列说法正确的是( )
甲
乙
A.开关S闭合瞬间,流经灯D2和D3的电流相等
B.开关S闭合瞬间至断开前,流经灯D1的电流保持不变
C.开关S断开瞬间,灯D2闪亮一下再熄灭
D.根据题中信息,可以推算出图乙中u1与u2的比值
6.(经典题)(多选题)如图所示,空间存在一范围足够大的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面(竖直面)向里,MM'为磁场区域的上边界,磁场上方有一个质量为m的正方形导线框abcd,ab边与MM'平行。已知线框边长为L,总电阻为R,重力加速度为g,ab边到MM'的初始高度为H,线框从图示位置由静止开始自由下落,则( )
A.H越大时,线框进入磁场的过程中,流过横截面的电荷量越多
B.H越大时,线框刚进入磁场时的加速度越大
C.若线框出现匀速运动,其速度大小一定是
D.线框进入磁场的过程中,机械能的减少量等于克服安培力做的功
7.如图所示,两根电阻不计、足够长的平行光滑金属导轨MN、PQ固定在水平面内,间距d=1 m,在导轨间宽度L=1 m的矩形区域内有垂直于导轨平面向上的匀强磁场,磁感应强度大小B=0.5 T,一根质量mb=0.2 kg、电阻R=0.5 Ω的金属棒b静止在导轨上,现使另一根质量ma=0.1 kg、电阻也为R=0.5 Ω的金属棒a以初速度v0=4 m/s从左端开始沿导轨滑动,穿过磁场区域后,与b发生弹性碰撞,两金属棒始终与导轨垂直且接触良好。求:
(1)金属棒a在第一次穿越磁场的过程中回路中感应电流的方向(从上向下看,是顺时针还是逆时针,写出结果即可);
(2)金属棒a在第一次穿越磁场的过程中流过金属棒a的电荷量q;
(3)金属棒a穿出磁场时的速度大小v1;
(4)在与金属棒b碰撞后,金属棒a的速度v2。
8.如图甲所示,足够长的光滑平行金属导轨JK、PQ倾斜放置,两导轨间距为L=1.0 m,导轨平面与水平面间的夹角为θ=30°,磁感应强度为B的匀强磁场垂直于导轨平面向上(图中未画出),导轨的J、P两端连接阻值为R=3.0 Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.90 kg,电阻r=0.50 Ω,重物的质量M=1.50 kg,如果将金属棒和重物由静止释放,金属棒沿导轨上滑的距离与时间的关系图像如图乙所示,不计导轨电阻,重力加速度g=10 m/s2。求:
(1)t=0时刻金属棒ab的加速度大小;
(2)求磁感应强度B的大小以及在1.2 s内通过电阻R的电荷量;
(3)在1.2 s内电阻R产生的热量。
甲
乙
迁移创新
9.一种可测速的跑步机的测速原理如图所示。该机底面固定有间距为L、宽度为d的平行金属电极。电极间充满磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,左侧接有电压表和电阻R。绝缘橡胶带上每隔距离d就嵌入一个电阻为r的平行细金属条,跑步过程中,绝缘橡胶带跟随脚步一起运动,金属条和电极之间接触良好且任意时刻仅有一根金属条处于磁场中。现在测出t时间内电压表读数恒为U,设人与跑步机间无相对滑动。
(1)判断电阻R中的电流方向。
(2)人跑步过程中,是否匀速 给出判断的理由。
(3)求t时间内人的平均跑步速度大小。
(4)若跑步过程中,人体消耗的能量有20%用于克服磁场力做功,求t时间内人体消耗的能量。
答案与分层梯度式解析
高考真题练
1.D 2.ABD 3.A 4.C 5.AD 6.A
7.AC 8.AD 9.D 10.AB 11.C 14.CD
1.D 题图乙所示情况下,穿过线圈的磁通量为0,A错误;由法拉第电磁感应定律可知,永磁铁相对线圈上升越快,磁通量变化越快,线圈中的感应电动势越大,永磁铁相对线圈上升越高时速度越小(点拨:永磁铁是上下振动的运动形式,故永磁铁相对线圈上升或下降的距离越大,速度越小),B、C错误;永磁铁相对线圈下降,穿过线圈的磁通量向外增大,由楞次定律结合安培定则可知,线圈中感应电流的方向为顺时针方向,D正确。
2.ABD MN最终受到重力和导轨的支持力保持静止,则一定静止于最低点OO'位置,A正确;根据楞次定律可知,MN运动过程中安培力始终做负功,B正确;从释放到第一次到达OO'位置的过程中,MN的速率先增大后减小,C错误;从释放到第一次到达OO'位置的过程中,根据右手定则可知MN中电流方向由M到N,D正确。
3.A 根据法拉第电磁感应定律可知,平均感应电动势E==,故A正确。
4.C
关键点拨 导体切割磁感线的有效长度是导体在垂直速度方向上的投影长度。
选取Oa直线段,由右手定则容易判断O点的电势高于a点的电势,排除B、D选项;A、C选项的主要区别是对b、c两点电势高低的判断,如图所示,导线Oab的等效长度为Ob,导线Oabc的等效长度为Oc,由几何关系可知Ob=Oc,b、c处的线速度大小相等,则UOb=UOc,故b、c两点的电势相等,C正确,A错误。
5.AD 杆OP匀速转动,由E=Bl2ω可知杆OP产生的感应电动势恒定,选项A正确;由右手定则可知,杆OP产生了由O到P的感应电流,则由左手定则可知MN会受到向左的安培力,在MN向左运动的过程中,由右手定则可判定MN切割磁感线产生由N到M的感应电动势,则通过MN的电流逐渐减小,由安培力F=BIl可知,杆MN、杆OP所受的安培力减小,杆MN做加速度减小的加速运动,故选项B、C错误,D正确。
6.A 金属棒切割磁感线产生的电动势E=BLv=2Bxv tan θ,电容器极板上的电荷量Q=CU=CE=2CBxv tan θ,通过金属棒的电流I===2BCv2 tan θ,选项A正确。金属棒到达x0时,Q=2BCx0v tan θ,B错误。根据右手定则,可知金属棒中电流从下向上流,上极板带正电,C错误。外力F=F安,F安=IBL,P=Fv=4B2Cv3x tan2 θ,则随着x的增加,P增加,D错误。
7.AC 设ab、cd导轨与x轴夹角为θ,过原点O时,金属棒有效长度为y0,则在0~ 时间内,金属棒切割磁感线的有效长度为y=y0+v0t tan θ,则产生的感应电动势E=Byv0=By0v0+Bt tan θ,感应电动势E与t是一次函数关系,则感应电流i与时间t是一次函数关系,在~时间内,金属棒切割磁感线的有效长度不变,所以感应电动势不变,感应电流不变,在~时间内相当于0~时间内的逆过程,因此选项A正确;由于不计电阻R之外的所有电阻,所以电阻R两端电压与感应电动势相等,选项D错误;当t=0、t=时,金属棒产生的感应电动势并不等于零,电流也不等于零,所以安培力并不等于0,选项B错误;在0~时间内,金属棒克服安培力做功的功率P=Fv0==(y0+v0t tan θ)2,P-t图线是抛物线的一部分,在~时间内切割磁感线有效长度不变,P=Fv0=,所以P恒定,在~时间内相当于0~时间内的逆过程,选项C正确。
8.AD 合上开关的瞬间,导体棒两端电压等于电容器两端电压且为最大值,电流也最大,I==,电流最大时,导体棒MN所受的安培力最大,而导体棒速度最大时电流不是最大,所以A正确,C错误;导体棒MN先加速后减速,不会匀速,如果导体棒MN做匀速直线运动,电阻上一直有焦耳热产生,其他能量都不变,不符合能量守恒定律,所以B错误;由于棒运动过程切割磁感线产生反电动势,导致只有开始时通过电阻R的电流与通过导体棒MN的电流相等,其他时候通过电阻R的电流都比通过导体棒MN的电流大,故由焦耳定律可知电阻R上产生的焦耳热比导体棒MN上产生的焦耳热多,D正确。
易混易错 导体棒加速时通过其电流由M到N,减速时电流由N到M。
9.D 根据右手定则可知,流过杆的感应电流方向为从M到N,A错误;由于杆在磁场中运动时会受到沿导轨向上的安培力,加速度逐渐减小,所以≠=v,则杆沿导轨下滑的距离不等于vt,故B错误;由于杆沿导轨下滑过程中只有安培力和重力做功,最终导体杆的速度增加,说明合外力做正功,也就是说运动过程中导体杆克服安培力做的功小于重力做的功,所以流过杆感应电流的平均电功率小于重力的平均功率,C错误;以沿导轨向下为正方向,根据动量定理可得mgt sin θ-I安=2mv-mv,解得杆所受安培力的冲量I安=mgt sin θ-mv,D正确。
10.AB 由右手定则可知回路中的电流方向为abcda,故A正确;导轨倾角θ=30°,ab棒稳定时有2mg· tan θ=F安=2BIL,得I==,B正确;加速时,对ab棒有2mg·sin θ-2BLI cos θ=2ma1,对cd棒有mg·sin θ-BLI cos θ=ma2,解得a1=a2=g sin θ-,加速度大小的表达式相同,C错误;由法拉第电磁感应定律可知E感=BLv cos θ,v、L、θ相同,但B不同,所以两棒产生的电动势不相等,D错误。
11.C 开关接1,导体棒处于静止状态时,其受力分析如图,可知tan =,而I=,解得E0=,选项A错误;
开关接2,导体棒从题图所示位置向左运动到左侧最高点过程中,根据右手定则可知,电流垂直纸面向里,即有电流通过二极管,则有安培力阻碍导体棒向左摆动,故棒在左侧的最大摆角小于,从左向右摆动过程中,根据右手定则可知二极管截止,没有电流经过,即没有安培力阻碍导体棒运动,最大摆角与左侧最大摆角相同,选项C正确;根据能量守恒定律可知,从右向左经过最低点的速度要大于从左向右经过最低点的速度,因此感应电动势并不等大,选项D错误;由于不知道棒运动到最左侧时的高度,所以无法计算棒消耗的焦耳热,选项B错误。
12.答案 (1) (2)- tan θ
解析 (1)感应电动势最大值Emax=Bω=BL2ω
感应电流最大值Imax=
CD棒所受安培力的最大值Fmax=BImaxL
解得Fmax=
感应电动势最小值Emin=BL2ω
感应电流最小值Imin=
CD棒所受安培力的最小值Fmin=BIminL=
(2)由题意知Fmax=mg sin θ+fm
Fmin=mg sin θ-fm
联立解得m=
CD棒沿导轨下滑,所受滑动摩擦力沿导轨向上,撤去推力瞬间,所受安培力大小等于(1)问中安培力的最大值,则CD棒的加速度方向沿导轨向上。
根据牛顿第二定律,Fmax+μmg cos θ-mg sin θ=ma
解得μ=- tan θ
方法技巧
导体转动切割磁感线产生感应电动势的求法
若长为L的导体棒在磁感应强度为B的匀强磁场中以角速度ω匀速转动,则
(1)以中点为轴时,E=0(不同两段的电动势的代数和为零)。
(2)以端点为轴时E=BωL2(平均速度取中点位置的线速度ωL)。
(3)以任意点为轴时E=Bω(-)(L1>L2,不同两段的电动势的代数和)。
13.答案 (1) (2)
解析 (1)设金属棒的速度为v,则感应电动势为E=Blv
感应电流为I==
金属棒所受的安培力为F安=BIl=
金属棒以速率v0匀速运动时,外力为F=F安1=
外力的功率为PF=Fv=
电阻R的热功率为PR=I2R=
依题意有:PF=2PR
解得v=
(2)金属棒相当于电源,电动势为E'=
设此时电容器的电压为UC,则电阻R的电压为UR=E'-UC
电阻R中的电流为I'=(点拨:电容器的部分为非纯电阻电路,只能通过电阻R应用欧姆定律求解电路的电流)
电阻R的热功率为PR'=URI'=
外力的功率即电源的功率,为
PF'=E'I'=
由题意有:PF'=2PR'
解得:UC==
电容器的电荷量为Q=CUC=
通过电源的电荷量也为Q,由电动势的定义得这段时间内非静电力做的功为W=QE'
解得W=
所以从断开S开始到此刻外力做的功为
归纳总结 (1)“匀速”→此时的安培力等于恒定外力。
(2)金属棒相当于电源,只有电阻R能应用欧姆定律,电容器的部分是非纯电阻电路。
(3)第(2)问中所涉及的是给电容器充电的过程,电路中的电流是变化的,但电源的电动势恒定不变。
(4)外力是变力,要应用W=qU进行巧妙的等效转化,简便地求出变力的功。
14.CD 金属杆通过光滑导轨时,根据动量定理得-BL·t1=mv-mv0,其中·t1=q1=;同理,金属杆通过粗糙导轨时,根据动量定理得-BL·t2-μmg·t2=0-mv,其中·t2=q2=,由此可知mv>mv0-mv,则金属杆经过BB1的速度v>,A错误;
根据能量守恒可知,整个回路中产生的总热量Q=m-μmgd,则定值电阻R上产生的热量QR==m-μmgd,B错误;金属杆所受安培力的冲量I=BL·t=BLq,而q=,所以金属杆经过AA1B1B与BB1C1C区域,安培力的冲量相同,C正确;由A项分析知--μmgt2=0-mv0,若将金属杆的初速度加倍,设金属杆在磁场中运动的距离为x,由动量定理知--μmgt3=0-m·2v0,由于t3
15.答案 (1) (2)m (3)
关键点拨 (1)注意Q棒是绝缘棒,不会有电流通过Q棒,且导轨光滑,说明Q棒与P棒碰撞前后Q棒均做匀速直线运动。
(2)P棒与Q棒滑出导轨后落在地面上同一点,说明P棒与Q棒滑出导轨时的速度相同。
(3)第(3)问求的是绝缘棒Q与金属棒P碰撞后在导轨上做匀速直线运动的时间。
解析 (1)由于绝缘棒Q与金属棒P的碰撞为弹性碰撞,金属导轨光滑,可知Q棒与P棒组成的系统动量守恒,机械能守恒,有3mv0=3mv'1+mv'2①
×3m=×3mv1'2+mv2'2②
联立①②得v'1=,v'2=v0
绝缘棒Q在水平方向所受合力为0,碰后做匀速直线运动,而P、Q落在地面同一点,可知P棒滑出导轨时的速度等于Q棒滑出导轨时的速度,即金属棒P滑出导轨时的速度大小为。
(2)由能量守恒定律可知,金属棒P减少的动能转化为运动过程中P棒产生的焦耳热,有
QP=mv2'2-mv1'2=m×-m×=m③
(3)对P棒回路由法拉第电磁感应定律有
=n (其中n=1)④
=⑤
q=·Δt⑥
联立④⑤⑥得q==⑦
可知碰撞后P的位移为
x=⑧
对P棒应用动量定理有
-BlΔt=mΔv⑨
整理有-Blq=mv'1-mv'2=-mv0
解得q=⑩
从Q与P碰撞到Q滑出导轨,Q与P在导轨上运动的位移相同,都是x,Q做匀速直线运动,则与P碰撞后,设绝缘棒Q在导轨上运动的时间为t'
t'=
联立①②⑧⑩可得t'=
16.答案 (1)BL (2)
(3)
解析 (1)设ab棒刚到MP处时的速度为v0,
由动能定理得mgL=m①
产生的电动势E0=BLv0②
由①②式得E0=BL
(2)将圆环分成4段,如图所示:由几何关系可知Rcf=R,Rde=R
由于导轨电阻不计,可认为cd、ef段被短路,圆环等效电阻R'==③
金属环中总电流I0=④
安培力大小F0=BI1L+BI2L=BI0L⑤
由牛顿第二定律有F0=2ma0⑥
由①~⑥式得a0=
(3)当棒ab的速度v1大于圆环速度v2时回路会有感应电流,安培力使ab减速,使圆环加速,直到ab速度等于圆环速度,此后圆环与棒ab一起匀速运动。设共同速度为vt,极短时间Δt内,由动量定理
对棒有BIL·Δt=mΔv1
对圆环BIL·Δt=2mΔv2
求和ΣBIL·Δt=Σm·Δv1
可得BLq=m(v0-vt)⑦
ΣBILΔt=Σ2mΔv2
可得BLq=2m·vt⑧
由⑦⑧式得
由闭合电路欧姆定律可得E1-E2=I·(R+R')
BLv1-BLv2=IR
BLv1Δt-BLv2Δt=IΔt·R
ΣBLv1Δt-ΣBLv2Δt=RΣIΔt
BLΣ(v1Δt-v2Δt)=RΣIΔt
BLΔx=Rq
Δx===
最小距离s=L+Δx=L+=
高考模拟练
1.A 2.BC 3.CD 4.AB 5.D 6.CD
1.A 按下按钮过程,穿过螺线管的磁通量向左且增大,根据楞次定律结合安培定则可知螺线管中感应电流为从P端流入从Q端流出,螺线管充当电源,则Q端电势较高;同理可知,松开按钮过程,P端电势较高,故A正确,B错误;按住按钮不动,穿过螺线管的磁通量不变,螺线管不会产生感应电动势,C错误;按下和松开按钮过程,螺线管中磁通量的变化率不一定相同,故螺线管产生的感应电动势不一定相同,D错误。
2.BC 开关S拨向2的瞬间,驱动线圈中的电流增大,线圈周围的磁场增强,根据楞次定律,发射线圈中的感应电流与驱动线圈中的电流反向,驱动线圈和发射线圈相互排斥,A错误,B正确;0~t0时间内,驱动线圈中的电流变化率逐渐减小,则周围磁感应强度的变化率逐渐减小,由法拉第电磁感应定律,发射线圈中的感应电动势减小,发射线圈中的电流不断减小,C正确;t0时刻后驱动线圈中电流减小,发射线圈中的感应电流与驱动线圈中的电流同向,驱动线圈和发射线圈相互吸引,发射线圈减速,只有选择合适的发射导管,使发射线圈在t0时刻能刚好到达管口,发射线圈的出射速度才最大,D错误。
方法技巧
根据图像分析问题的三个关键点
(1)弄清图像所揭示的物理规律或物理量间的函数关系。
(2)挖掘图像中的隐含条件,明确有关图线所包围的面积、图线的斜率(或其绝对值)、截距所表示的物理意义。
(3)借助有关的物理概念、公式、定理和定律做出分析判断。
3.CD 由右手定则可知,线圈中的电流方向为逆时针与顺时针交替变化,故A错误。跳楼机由静止下落后受安培力与重力,根据牛顿第二定律有mg-F安=ma,且安培力F安=2nBIL,E=2nBLv,I=,联立可得mg-=ma;随着速度的增大,加速度减小,当加速度为0时,速度达到最大值,以后跳楼机做匀速运动;当跳楼机速度最大时,安培力与重力平衡,有mg=F安m=,解得vm=2 m/s,此时克服安培力做功的功率为P安=F安m·vm=mgvm=640×10×2 W=12 800 W,故B错误,D正确。当跳楼机的速度为1 m/s时,线圈中的感应电流为I=== A=20 A,C正确。
4.AB 由于导线框做匀速运动,可知水平外力和安培力F大小相等,方向相反。导线框进入磁场的过程中,安培力为F=BIl=,B、l、v不变,则F不变,水平外力的冲量I=-Ft=-;完全进入磁场后,感应电流为零,安培力为零,故外力为零,冲量不变,A正确,D错误。进入磁场的过程中,有Uab=RI电=Blv,完全进入磁场后,a、b两点间的电势差为Uab=Blv,B正确;进入磁场的过程中,q=Δt==,完全进入磁场后感应电流为零,q不变,但不为零,C错误。
5.D 开关S闭合瞬间,D2立即发光,由于电感线圈L的自感,阻碍电流的增大,流经灯D3的电流小于流经D2的电流,A错误。开关闭合瞬间,电路等效于灯D1和D2串联,待稳定后,灯D2和D3并联后再与灯D1串联,总电阻比开关闭合瞬间小,故从开关S闭合瞬间至断开前,流经灯D1的电流是变化的,B错误。开关S断开前,流经灯D2和D3的电流相等,开关S断开瞬间,线圈L产生自感电动势阻碍电流的减小,由线圈L为灯D2和D3供电,流经灯D2的电流并没有突然增大,D2不会闪亮,只是逐渐熄灭,C错误。开关S闭合瞬间,电压传感器所在支路相当于断路,电路等效于灯D1和D2串联,电压传感器所测电压为D2两端电压,由串联分压规律可知u1=;电路稳定后,由欧姆定律可知流过D3的电流为I=·=;开关S断开瞬间,电感线圈L能够为D2和D3提供与之前等大的电流,其两端电压为u2=I·2R=,所以=,故可以推算出题图乙中u1与u2的比值,D正确。
6.CD 线框进入磁场过程中,平均感应电动势为=,平均感应电流为=,则线框进入磁场的过程中,流过横截面的电荷量为q=Δt==,可知流过横截面的电荷量与下落高度无关,故A错误。根据题意可知,ab边进入磁场前线框做自由落体运动,由v2=2gh可得,线框刚进入磁场时的速度为v=,产生的感应电动势为E=BLv,感应电流为I=,安培力为F=BIL=,由右手定则和左手定则可知,安培力竖直向上;若线框匀速运动,则有=mg,联立解得v=,H=;可知,若H>,则线框进入磁场时,安培力大于重力,由牛顿第二定律有-mg=ma,可知H越大,进入磁场时的加速度越大;若H<,则线框进入磁场时,安培力小于重力,由牛顿第二定律有mg-=ma,可知H越大,进入磁场时的加速度越小,故B错误,C正确。线框进入磁场的过程中,除了重力之外只有安培力做功,由功能关系可知,机械能的减少量等于克服安培力做的功,故D正确。
7.答案 (1)逆时针 (2)0.5 C (3)1.5 m/s
(4)0.5 m/s,方向向左
解析 (1)由右手定则可知,金属棒a第一次穿越磁场时回路中有逆时针方向的感应电流。
(2)金属棒a在第一次穿越磁场的过程中,平均感应电动势=,通过金属棒a的电荷量q=·Δt=·Δt=== C=0.5 C。
(3)金属棒a第一次穿越磁场的过程中,由动量定理可得
-BdΔt=mav1-mav0
q=·Δt=0.5 C
代入数据解得v1=1.5 m/s。
(4)两棒发生弹性碰撞,以向右为正方向,由动量守恒定律有mav1=mav2+mbv
由机械能守恒由ma=ma+mbv2
代入解得v2=-0.5 m/s,负号表示速度方向向左。
8.答案 (1)4.375 m/s2 (2) T C
(3)9.45 J
解析 (1)以金属棒ab和重物整体为研究对象,t=0时刻,根据牛顿第二定律得
Mg-mg sin θ=(M+m)a
解得a=4.375 m/s2。
(2)由题图乙可以看出,最终金属棒ab将匀速运动,匀速运动的速度为v== m/s=1.75 m/s
此时金属棒ab切割磁感线产生的感应电动势E=BLv
感应电流 I=
金属棒ab所受的安培力 F=BIL=
金属棒ab匀速运动时,金属棒和重物整体受力平衡,可得 F+mg sin θ=Mg
联立解得B= T
在1.2 s内通过电阻R的电荷量 q=== C。
(3)对金属棒和重物整体,由能量守恒定律得Mgs=mgs sin θ+Q+(M+m)v2
且有 QR=Q
联立解得QR=9.45 J。
方法技巧 电荷量、磁通量的变化量、安培力的冲量间的关系
设想在某一回路中,一金属杆运动时,感应电流在改变,安培力F为变力。
设在Δt时间内的平均电流为,平均感应电动势为,则=,==,
Δt时间内通过金属杆的电荷量q=Δt=;
设在Δt时间内的平均安培力为,平均电流为,安培力的冲量为I=Δt=BLΔt,
通过金属杆的电荷量q=Δt=。
9.答案 (1)向下 (2)见解析 (3)U
(4)
解析 (1)由题意根据右手定则可知,电阻R中的电流方向向下。
(2)(3)金属条做切割磁感线运动产生的感应电动势大小为E=BLv,
回路中的电流大小为I=,
电压表的示数为U=IR,
解得v=U,
由于电压表示数恒定,所以金属条的运动速度也恒定,说明人跑步过程中是匀速的。
人的平均跑步速度大小等于金属条的运动速度,为
v'=U。
(4)金属条中的电流为I=,
金属条受到的安培力大小为FA=ILB,
t时间内金属条克服安培力做的功为
W=FAvt==,
所以t时间内人体消耗的能量
E==。
方法创新 本题属于理论联系实际问题,关键是建立物理模型——“单杆模型”,人跑动时带动绝缘橡胶带上固定的细金属条运动,当细金属条在磁场中运动时切割磁感线,产生感应电动势,给电阻供电,通过电压表可读出路端电压,然后分析各个问题。
10
同课章节目录
