1.3 正方形的性质与判定(第1课时)教学设计(表格式)北师大版数学九年级上册
文档属性
| 名称 | 1.3 正方形的性质与判定(第1课时)教学设计(表格式)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 332.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 21:45:17 | ||
图片预览


文档简介
3 正方形的性质与判定
课题 第1课时 正方形的性质 授课类型 新授课
授课人
教学内容 课本P20-21
教学目标 1.理解正方形的概念,了解它与菱形、矩形、平行四边形之间的关系。 2.探索并证明正方形的性质,进一步发展推理能力。 3.体会探索与证明过程中所蕴含的抽象、推理等数学思想。
教学重难点 重点:探索并证明正方形的性质定理。 难点:掌握正方形的性质的应用方法。
教学准备 多媒体课件、矩形纸张、活动的菱形框架。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 下列图片中出现的四边形都是特殊的平行四边形。观察这些特殊的平行四边形,你能发现它们有什么样的共同特征吗? 师生活动:教师出示问题,学生回答,然后教师引出课题。 学生回答:这些特殊的平行四边形均是正方形。 这节课我们就来研究正方形的概念及性质。(教师板书课题: 第1课时 正方形的性质) 教师活动:同学们观察显示的图片后,有什么联想?正方形的四条边有什么关系?四个角呢? 学生活动:观察屏幕上所展示的生活中的正方形图片,进行联想.易知:正方形四条边都相等(小学已学过);正方形四个角都是直角(小学已学过)。 【归纳结论】 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
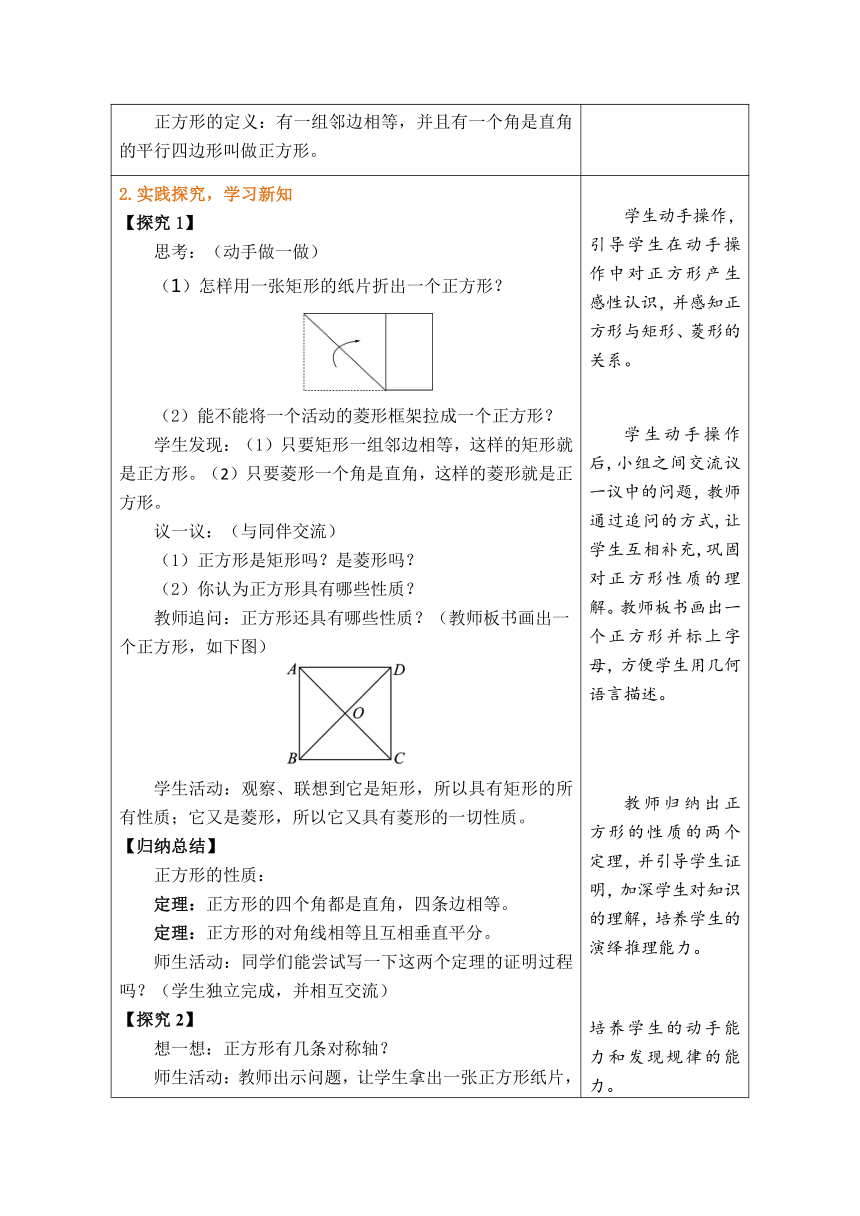
2.实践探究,学习新知 【探究1】 思考:(动手做一做) (1)怎样用一张矩形的纸片折出一个正方形? (2)能不能将一个活动的菱形框架拉成一个正方形? 学生发现:(1)只要矩形一组邻边相等,这样的矩形就是正方形。(2)只要菱形一个角是直角,这样的菱形就是正方形。 议一议:(与同伴交流) (1)正方形是矩形吗?是菱形吗? (2)你认为正方形具有哪些性质? 教师追问:正方形还具有哪些性质?(教师板书画出一个正方形,如下图) 学生活动:观察、联想到它是矩形,所以具有矩形的所有性质;它又是菱形,所以它又具有菱形的一切性质。 【归纳总结】 正方形的性质: 定理:正方形的四个角都是直角,四条边相等。 定理:正方形的对角线相等且互相垂直平分。 师生活动:同学们能尝试写一下这两个定理的证明过程吗?(学生独立完成,并相互交流) 【探究2】 想一想:正方形有几条对称轴? 师生活动:教师出示问题,让学生拿出一张正方形纸片,折一折,观察、思考、发现结论并与同伴交流。 总结:正方形是轴对称图形,它有四条对称轴。 【教材例题】 例1 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF。 BE与DF之间有怎样的关系?请说明理由。 教师活动:操作投影仪.组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:BE=DF,且BE⊥DF。理由如下: (1)∵四边形ABCD是正方形, ∴BC=DC,∠BCE=90°(正方形的四条边相等,四个角都是直角)。 ∴∠DCE=180°-∠BCE=180°-90°=90°。 ∴∠BCE=∠DCF。 又∵CE=CF, ∴△BCE≌△DCE。 ∴BE=DF。 (2)延长BE交DF于点M(如图)。 ∵△BCE≌△DCE, ∴∠CBE=∠CDF。 ∵∠DCF=90°, ∴∠CDF+∠F=90°, ∴∠CBE+∠F=90°, ∴∠BMF=90°, ∴BE⊥DF。 议一议:议平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗? 师生活动:教师出示问题,让学生尝试表示它们之间的关系,教师引导。 学生动手操作,引导学生在动手操作中对正方形产生感性认识,并感知正方形与矩形、菱形的关系。 学生动手操作后,小组之间交流议一议中的问题,教师通过追问的方式,让学生互相补充,巩固对正方形性质的理解。教师板书画出一个正方形并标上字母,方便学生用几何语言描述。 教师归纳出正方形的性质的两个定理,并引导学生证明,加深学生对知识的理解,培养学生的演绎推理能力。 培养学生的动手能力和发现规律的能力。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。 小组交流,引导学生从角、对角线的角度归纳总结。让学生整体地理解平行四边形、菱形、矩形、正方形之间的关系,并能直观地表示这种关系。
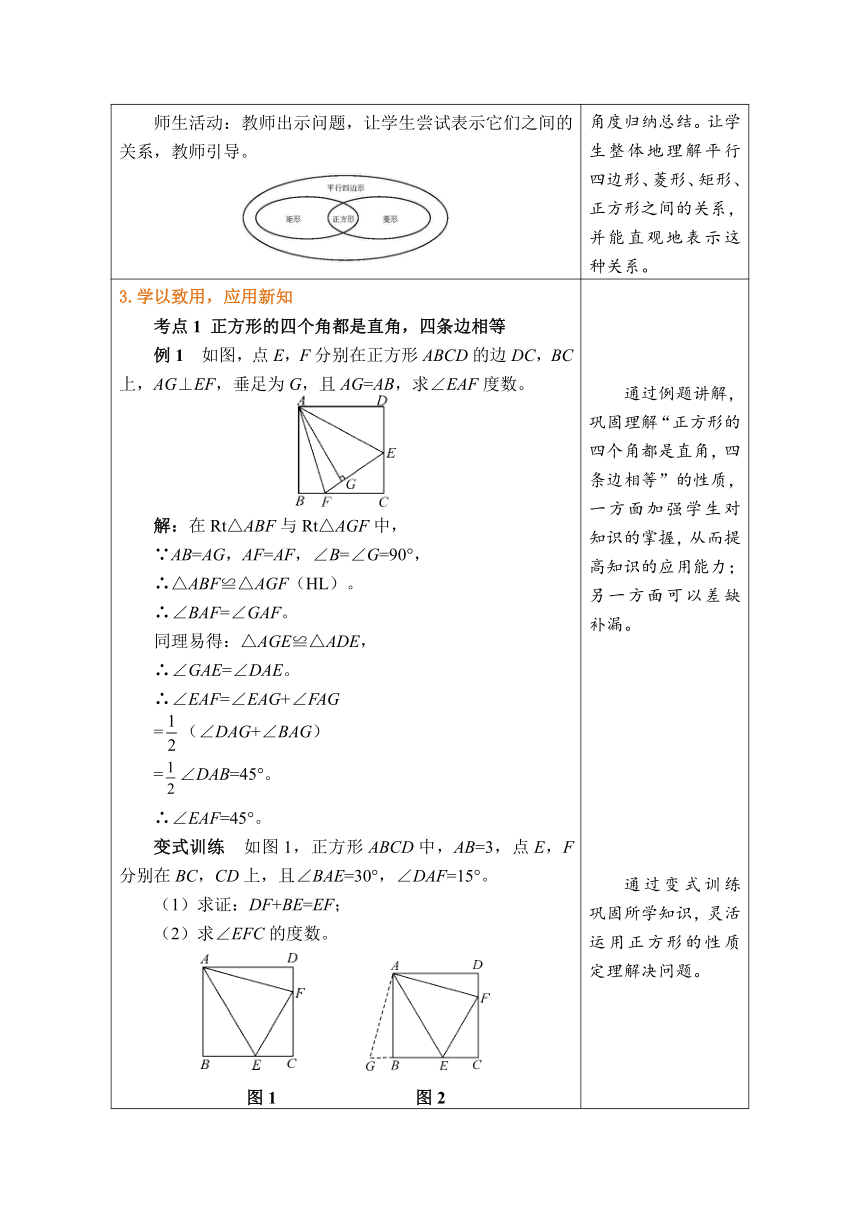
3.学以致用,应用新知 考点1 正方形的四个角都是直角,四条边相等 例1 如图,点E,F分别在正方形ABCD的边DC,BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF度数。 解:在Rt△ABF与Rt△AGF中, ∵AB=AG,AF=AF,∠B=∠G=90°, ∴△ABF≌△AGF(HL)。 ∴∠BAF=∠GAF。 同理易得:△AGE≌△ADE, ∴∠GAE=∠DAE。 ∴∠EAF=∠EAG+∠FAG =(∠DAG+∠BAG) =∠DAB=45°。 ∴∠EAF=45°。 变式训练 如图1,正方形ABCD中,AB=3,点E,F分别在BC,CD上,且∠BAE=30°,∠DAF=15°。 (1)求证:DF+BE=EF; (2)求∠EFC的度数。 图1 图2 解:(1)证明:如图2,延长EB至G,使BG=DF,连接AG。 ∵四边形ABCD是正方形, ∴AB=AD,∠ABG=∠ADF=∠BAD=90°。 ∵BG=DF, ∴△ABG≌△ADF。 ∴AG=AF。 ∵∠BAE=30°,∠DAF=15°, ∴∠FAE=∠GAE=45°。 ∵AE=AE, ∴△FAE≌△GAE。 ∴EF=EG=GB+BE=DF+BE。 (2)∵△AGE≌△AFE, ∴∠AFE=∠AGE=∠DFA=90°-∠DAF=75°。 ∴∠EFC=180°-∠DFA-∠AFE=180°-75°-75°=30°。 ∴∠EFC=30°。 考点2 正方形的对角线相等且互相平分 例2 如图,在正方形ABCD中,AB=1,P是线段AD上的动点,PE⊥AC,PF⊥BD,垂足分别为E,F,则PE+PF的值为( ) A. B. 4 C. 2 D. 答案:D 变式训练 如图,两个边长为4的正方形重叠在一起,点O是其中一个正方形的中心,则图中阴影部分的面积为_______。 答案:4 通过例题讲解,巩固理解“正方形的四个角都是直角,四条边相等”的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用正方形的性质定理解决问题。 通过例题讲解,巩固理解“正方形的对角线相等且互相平分”的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 平行四边形、矩形、菱形、正方形都具有的是( ) A. 对角线互相平分 B. 对角线互相垂直 C. 对角线相等 D. 对角线互相垂直且相等 答案:A 2. 如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( ) A. 5 B. 6 C. 7 D. 8 答案:B 3. 在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是________。 答案:22.5° 4. 如图,正方形CEGF的顶点E,F在正方形ABCD的边BC,CD上,且AB=5,CE=3,连接BG,DG,则图中阴影部分的面积是_______。 答案:8 5. 如图,正方形ABCD的边长为1 cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长。 解:∵四边形ABCD为正方形, ∴∠B=90°,∠ACB=45°,AB=BC=1 cm。 ∵EF⊥AC, ∴∠EFA=∠EFC=90°。 又∵∠ECF=45°, ∴△EFC是等腰直角三角形。 ∴EF=FC。 ∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE, ∴△ABE≌△AFE。 ∴AB=AF=1cm,BE=EF。 ∴FC=BE。 在Rt△ABC中,AC== cm, ∴FC=AC-AF=(-1)cm。 ∴BE=(-1)cm。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。 2.正方形的性质: 定理:正方形的四个角都是直角,四条边相等。 定理:正方形的对角线相等且互相垂直平分。 正方形是轴对称图形,它有四条对称轴。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P22习题1.7中的T1、T2、T3、T※4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 正方形的性质一、正方形的定义二、正方形的性质投影区1.定理2.定理3.对称性学生活动区
提纲掣领,重点突出。
教后反思 创设情境导入,新授知识层层递进、联系密切,过渡自然,调动学生的学习热情,注意力集中不分散。 让学生在知道正方形是特殊的菱形和矩形的基础上,小组讨论得出正方形的性质,有利于学生的自主学习。通过学生的动手操作,讨论如何将矩形折成正方形、如何将菱形拉成正方形,培养学生的动手能力和思维能力。本课虽然是学习正方形的性质,实际上应起到对平行四边形、矩形、菱形性质的复习、归纳和总结的作用,培养学生的发散思维能力。 教学中鼓励学生大胆探索新颖独特的解题思路和解题方法,提倡解题方法的多样性,并引导学生在与他人的交流中比较解题方法的异同,有利于提高学生的逻辑思维水平。 反思,更进一步提升。
课题 第1课时 正方形的性质 授课类型 新授课
授课人
教学内容 课本P20-21
教学目标 1.理解正方形的概念,了解它与菱形、矩形、平行四边形之间的关系。 2.探索并证明正方形的性质,进一步发展推理能力。 3.体会探索与证明过程中所蕴含的抽象、推理等数学思想。
教学重难点 重点:探索并证明正方形的性质定理。 难点:掌握正方形的性质的应用方法。
教学准备 多媒体课件、矩形纸张、活动的菱形框架。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 下列图片中出现的四边形都是特殊的平行四边形。观察这些特殊的平行四边形,你能发现它们有什么样的共同特征吗? 师生活动:教师出示问题,学生回答,然后教师引出课题。 学生回答:这些特殊的平行四边形均是正方形。 这节课我们就来研究正方形的概念及性质。(教师板书课题: 第1课时 正方形的性质) 教师活动:同学们观察显示的图片后,有什么联想?正方形的四条边有什么关系?四个角呢? 学生活动:观察屏幕上所展示的生活中的正方形图片,进行联想.易知:正方形四条边都相等(小学已学过);正方形四个角都是直角(小学已学过)。 【归纳结论】 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
2.实践探究,学习新知 【探究1】 思考:(动手做一做) (1)怎样用一张矩形的纸片折出一个正方形? (2)能不能将一个活动的菱形框架拉成一个正方形? 学生发现:(1)只要矩形一组邻边相等,这样的矩形就是正方形。(2)只要菱形一个角是直角,这样的菱形就是正方形。 议一议:(与同伴交流) (1)正方形是矩形吗?是菱形吗? (2)你认为正方形具有哪些性质? 教师追问:正方形还具有哪些性质?(教师板书画出一个正方形,如下图) 学生活动:观察、联想到它是矩形,所以具有矩形的所有性质;它又是菱形,所以它又具有菱形的一切性质。 【归纳总结】 正方形的性质: 定理:正方形的四个角都是直角,四条边相等。 定理:正方形的对角线相等且互相垂直平分。 师生活动:同学们能尝试写一下这两个定理的证明过程吗?(学生独立完成,并相互交流) 【探究2】 想一想:正方形有几条对称轴? 师生活动:教师出示问题,让学生拿出一张正方形纸片,折一折,观察、思考、发现结论并与同伴交流。 总结:正方形是轴对称图形,它有四条对称轴。 【教材例题】 例1 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF。 BE与DF之间有怎样的关系?请说明理由。 教师活动:操作投影仪.组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:BE=DF,且BE⊥DF。理由如下: (1)∵四边形ABCD是正方形, ∴BC=DC,∠BCE=90°(正方形的四条边相等,四个角都是直角)。 ∴∠DCE=180°-∠BCE=180°-90°=90°。 ∴∠BCE=∠DCF。 又∵CE=CF, ∴△BCE≌△DCE。 ∴BE=DF。 (2)延长BE交DF于点M(如图)。 ∵△BCE≌△DCE, ∴∠CBE=∠CDF。 ∵∠DCF=90°, ∴∠CDF+∠F=90°, ∴∠CBE+∠F=90°, ∴∠BMF=90°, ∴BE⊥DF。 议一议:议平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗? 师生活动:教师出示问题,让学生尝试表示它们之间的关系,教师引导。 学生动手操作,引导学生在动手操作中对正方形产生感性认识,并感知正方形与矩形、菱形的关系。 学生动手操作后,小组之间交流议一议中的问题,教师通过追问的方式,让学生互相补充,巩固对正方形性质的理解。教师板书画出一个正方形并标上字母,方便学生用几何语言描述。 教师归纳出正方形的性质的两个定理,并引导学生证明,加深学生对知识的理解,培养学生的演绎推理能力。 培养学生的动手能力和发现规律的能力。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。 小组交流,引导学生从角、对角线的角度归纳总结。让学生整体地理解平行四边形、菱形、矩形、正方形之间的关系,并能直观地表示这种关系。
3.学以致用,应用新知 考点1 正方形的四个角都是直角,四条边相等 例1 如图,点E,F分别在正方形ABCD的边DC,BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF度数。 解:在Rt△ABF与Rt△AGF中, ∵AB=AG,AF=AF,∠B=∠G=90°, ∴△ABF≌△AGF(HL)。 ∴∠BAF=∠GAF。 同理易得:△AGE≌△ADE, ∴∠GAE=∠DAE。 ∴∠EAF=∠EAG+∠FAG =(∠DAG+∠BAG) =∠DAB=45°。 ∴∠EAF=45°。 变式训练 如图1,正方形ABCD中,AB=3,点E,F分别在BC,CD上,且∠BAE=30°,∠DAF=15°。 (1)求证:DF+BE=EF; (2)求∠EFC的度数。 图1 图2 解:(1)证明:如图2,延长EB至G,使BG=DF,连接AG。 ∵四边形ABCD是正方形, ∴AB=AD,∠ABG=∠ADF=∠BAD=90°。 ∵BG=DF, ∴△ABG≌△ADF。 ∴AG=AF。 ∵∠BAE=30°,∠DAF=15°, ∴∠FAE=∠GAE=45°。 ∵AE=AE, ∴△FAE≌△GAE。 ∴EF=EG=GB+BE=DF+BE。 (2)∵△AGE≌△AFE, ∴∠AFE=∠AGE=∠DFA=90°-∠DAF=75°。 ∴∠EFC=180°-∠DFA-∠AFE=180°-75°-75°=30°。 ∴∠EFC=30°。 考点2 正方形的对角线相等且互相平分 例2 如图,在正方形ABCD中,AB=1,P是线段AD上的动点,PE⊥AC,PF⊥BD,垂足分别为E,F,则PE+PF的值为( ) A. B. 4 C. 2 D. 答案:D 变式训练 如图,两个边长为4的正方形重叠在一起,点O是其中一个正方形的中心,则图中阴影部分的面积为_______。 答案:4 通过例题讲解,巩固理解“正方形的四个角都是直角,四条边相等”的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用正方形的性质定理解决问题。 通过例题讲解,巩固理解“正方形的对角线相等且互相平分”的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 平行四边形、矩形、菱形、正方形都具有的是( ) A. 对角线互相平分 B. 对角线互相垂直 C. 对角线相等 D. 对角线互相垂直且相等 答案:A 2. 如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( ) A. 5 B. 6 C. 7 D. 8 答案:B 3. 在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是________。 答案:22.5° 4. 如图,正方形CEGF的顶点E,F在正方形ABCD的边BC,CD上,且AB=5,CE=3,连接BG,DG,则图中阴影部分的面积是_______。 答案:8 5. 如图,正方形ABCD的边长为1 cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长。 解:∵四边形ABCD为正方形, ∴∠B=90°,∠ACB=45°,AB=BC=1 cm。 ∵EF⊥AC, ∴∠EFA=∠EFC=90°。 又∵∠ECF=45°, ∴△EFC是等腰直角三角形。 ∴EF=FC。 ∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE, ∴△ABE≌△AFE。 ∴AB=AF=1cm,BE=EF。 ∴FC=BE。 在Rt△ABC中,AC== cm, ∴FC=AC-AF=(-1)cm。 ∴BE=(-1)cm。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。 2.正方形的性质: 定理:正方形的四个角都是直角,四条边相等。 定理:正方形的对角线相等且互相垂直平分。 正方形是轴对称图形,它有四条对称轴。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P22习题1.7中的T1、T2、T3、T※4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 正方形的性质一、正方形的定义二、正方形的性质投影区1.定理2.定理3.对称性学生活动区
提纲掣领,重点突出。
教后反思 创设情境导入,新授知识层层递进、联系密切,过渡自然,调动学生的学习热情,注意力集中不分散。 让学生在知道正方形是特殊的菱形和矩形的基础上,小组讨论得出正方形的性质,有利于学生的自主学习。通过学生的动手操作,讨论如何将矩形折成正方形、如何将菱形拉成正方形,培养学生的动手能力和思维能力。本课虽然是学习正方形的性质,实际上应起到对平行四边形、矩形、菱形性质的复习、归纳和总结的作用,培养学生的发散思维能力。 教学中鼓励学生大胆探索新颖独特的解题思路和解题方法,提倡解题方法的多样性,并引导学生在与他人的交流中比较解题方法的异同,有利于提高学生的逻辑思维水平。 反思,更进一步提升。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
