22.1.2 二次函数y=ax2的图象和性质 同步练习(含答案)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.2 二次函数的图象和性质
基础提优题
1.关于二次函数的图象,下列说法错误的是( )
A.它是一条抛物线 B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点 D.当x>0时,y随x的增大而增大
2.若二次函数的图象经过点P(-2,4),则该图象必经过点( )
A.(2,4) B.(-2,-4) C.(-4,2) D.(4,-2)
3.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出二次函数与的图象,则阴影部分的面积是( )
A.4 B.6 C.8 D.12
4.已知抛物线经过两点,则下列关系式一定正确的是( )
5.已知二次函数当0时,y随x的增大而减小,则实数a的值可能是_______________.(写出一个即可)
6.如图所示,三个二次函数的图象分别对应的是则a ,a ,a 的大小关系是_____________.
7.已知是二次函数,且当时,y随x的增大而增大.
(1)求k的值,并画出它的图象;
(2)写出该函数图象的对称轴和顶点坐标;
(3)如果点P(m,n)是此二次函数图象上的一点,若,求n的取值范围.
综合应用题
8.二次函数与一次函数在同一坐标系中的大致图象可能是
( )
9.如图,在平面直角坐标系中,平行于x轴的直线y=2,与二次函数分别交于点A,B和点C,D,若CD=2AB,则a=( )
A.4 B. C.2 D.
10.如图,直线y=kx+b(k≠0)与抛物线(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论中,正确的有( )
①抛物线图象的顶点一定是原点;
②当时,直线.与抛物线的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当时,
A.①② B.①②⑤ C.②③④ D.①②④⑤
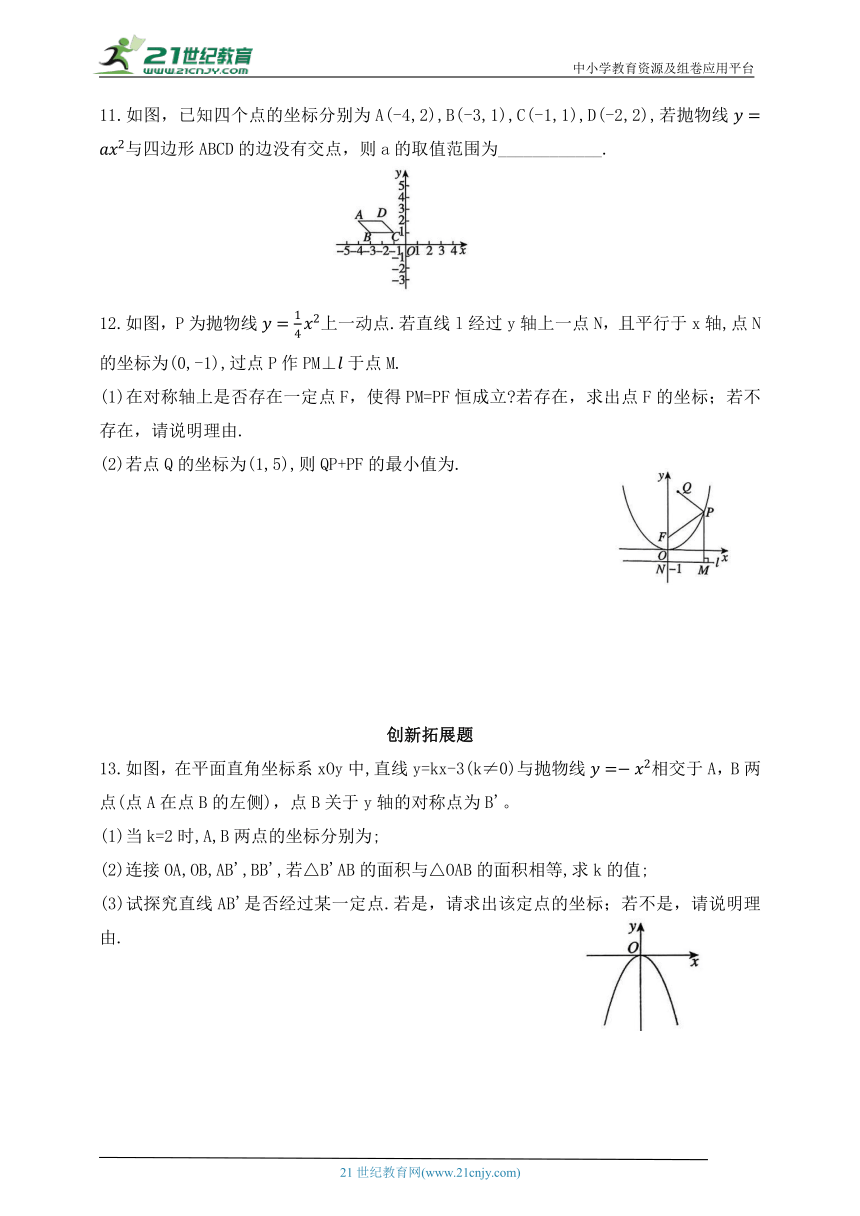
11.如图,已知四个点的坐标分别为A(-4,2),B(-3,1),C(-1,1),D(-2,2),若抛物线与四边形ABCD的边没有交点,则a的取值范围为____________.
12.如图,P为抛物线上一动点.若直线l经过y轴上一点N,且平行于x轴,点N的坐标为(0,-1),过点P作PM⊥于点M.
(1)在对称轴上是否存在一定点F,使得PM=PF恒成立 若存在,求出点F的坐标;若不存在,请说明理由.
(2)若点Q的坐标为(1,5),则QP+PF的最小值为.
创新拓展题
13.如图,在平面直角坐标系xOy中,直线y=kx-3(k≠0)与抛物线相交于A,B两点(点A在点B的左侧),点B关于y轴的对称点为B'。
(1)当k=2时,A,B两点的坐标分别为;
(2)连接OA,OB,AB',BB',若△B'AB的面积与△OAB的面积相等,求k的值;
(3)试探究直线AB'是否经过某一定点.若是,请求出该定点的坐标;若不是,请说明理由.
参考答案
1.C 2.A 3.C 4.C 5.0(答案不唯一)
7.【解】(1)根据题意,得解得(舍去).
∴二次函数的解析式为其图象如图所示.
(2)该函数图象的对称轴为y轴,顶点坐标为(0,0).
(3)∵点P(m,n)是此二次函数图象上的一点,且-2≤m≤1,
∴当m=-2时,
当m=1时,
当m=0时,n取最大值,n=0.
∴当-2≤m≤1时,-4≤n≤0.
8.D
9.B【点拨】设直线AB与y轴交于点E.∵直线y=2与二次函数交于A,B两点,∴当y=2时,得x=±,∴A(-,2),B(,2).∴AB=2.又∵CD=2AB,由二次函数图象的对称性可得CE=将点D的坐标代入y=ax ,得8a=2,解得
10.B【点拨】①抛物线顶点坐标为(0,0),故①说法正确,符合题意;②由题图可知,k>0,a>0,二次函数的顶点坐标为(0.0),所以当x>0时,直线y=kx+b(k≠0)与抛物线的函数值都随着x的增大而增大,故②说法正确,符合题意;③由点A的横坐标是-2,点B的横坐标是3,若AB=5,可得出直线AB与x轴平行,即k=0,与已知k≠0矛盾,故③说法错误,不符合题意;④当△OAB为等边三角形时,有OA=OB,可得出直线AB与x轴平行,即.k=0,与已知k≠0矛盾,故④说法错误,不符合题意;⑤由可知,所以判断直线y=kx+b(k≠0)的图象在抛物线的上方时,x的取值范围,结合两者交点A,B的横坐标可得,-211.或或【点拨】①当a<0时,恒成立;②当a>0时,将点C(-1,1)的坐标代入.y=ax ,得a=1,将点B(-3,1)的坐标代入得将点A(-4,2)的坐标代入y=ax ,得∵抛物线与四边形ABCD的边没有交点,∴a>1或
12.【解】(1)存在一定点F,使得PM=PF恒成立.
过点P作PB⊥y轴于点B.
设点P的坐标为∴易知
又∵PB=a,∴在Rt△PBF中,.
∴OF=1.∴点F的坐标为(0,1).
(2)6【点拨】由(1),得PM=PF,∴QP+PF的最小值为QP+PM的最小值.∴当Q,P,M三点共线时,QP+PM有最小值,最小值为点Q的纵坐标加点M的纵坐标的绝对值.∴QP+PF的最小值为6.
13.【解】(1)(-3,-9),(1,-1)
(2)∵A,B是抛物线图象上的两点,
设A(m,-m ),B(n,-n ),则
当k>0时,如图①,
根据题意,得整理,得
易知m,n是的两个根,∴.
设直线y=kx-3与y轴的交点为D,则点D(0,-3),∴OD=3.
∵易知且S△NAB。n)(m-n),∴3=-2n×(m+n)=2nk,∴2nk=-mn.
又∵n≠0,∴m=-2k.∴n=k.∴-2k×k=-3,解得或(舍去),故
当k<0时,如图②,
根据题意,得整理,得
易知m,n是的两个根,∴m+n=-k,mn=-3.
设直线y=kx-3与y轴的交点为D,则点D(0,-3),∴OD=3,
∵易知m).∴3=2n×(m+n)=-2nk.∴-2nk=-mn.
又∵n≠0,∴m=2k.∴n=-3k.∴2k×(-3k)=-3,
解得或(舍去),故
综上所述,k的值为或
(3)直线AB'一定经过定点(0,3).
∵A,B是抛物线图象上的两点,
∴设A(m,-m ),B(n,-n ),则.
根据题意,得整理,得
易知m,n是的两个根,∴m+n=-k,mn=-3.设直线AB'的函数解析式为y=px+q,根据题意,得解得
∴直线AB'的函数解析式为.
∴直线AB'的函数解析式为.
∴直线.AB'一定经过定点(0,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.2 二次函数的图象和性质
基础提优题
1.关于二次函数的图象,下列说法错误的是( )
A.它是一条抛物线 B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点 D.当x>0时,y随x的增大而增大
2.若二次函数的图象经过点P(-2,4),则该图象必经过点( )
A.(2,4) B.(-2,-4) C.(-4,2) D.(4,-2)
3.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出二次函数与的图象,则阴影部分的面积是( )
A.4 B.6 C.8 D.12
4.已知抛物线经过两点,则下列关系式一定正确的是( )
5.已知二次函数当0时,y随x的增大而减小,则实数a的值可能是_______________.(写出一个即可)
6.如图所示,三个二次函数的图象分别对应的是则a ,a ,a 的大小关系是_____________.
7.已知是二次函数,且当时,y随x的增大而增大.
(1)求k的值,并画出它的图象;
(2)写出该函数图象的对称轴和顶点坐标;
(3)如果点P(m,n)是此二次函数图象上的一点,若,求n的取值范围.
综合应用题
8.二次函数与一次函数在同一坐标系中的大致图象可能是
( )
9.如图,在平面直角坐标系中,平行于x轴的直线y=2,与二次函数分别交于点A,B和点C,D,若CD=2AB,则a=( )
A.4 B. C.2 D.
10.如图,直线y=kx+b(k≠0)与抛物线(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论中,正确的有( )
①抛物线图象的顶点一定是原点;
②当时,直线.与抛物线的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当时,
A.①② B.①②⑤ C.②③④ D.①②④⑤
11.如图,已知四个点的坐标分别为A(-4,2),B(-3,1),C(-1,1),D(-2,2),若抛物线与四边形ABCD的边没有交点,则a的取值范围为____________.
12.如图,P为抛物线上一动点.若直线l经过y轴上一点N,且平行于x轴,点N的坐标为(0,-1),过点P作PM⊥于点M.
(1)在对称轴上是否存在一定点F,使得PM=PF恒成立 若存在,求出点F的坐标;若不存在,请说明理由.
(2)若点Q的坐标为(1,5),则QP+PF的最小值为.
创新拓展题
13.如图,在平面直角坐标系xOy中,直线y=kx-3(k≠0)与抛物线相交于A,B两点(点A在点B的左侧),点B关于y轴的对称点为B'。
(1)当k=2时,A,B两点的坐标分别为;
(2)连接OA,OB,AB',BB',若△B'AB的面积与△OAB的面积相等,求k的值;
(3)试探究直线AB'是否经过某一定点.若是,请求出该定点的坐标;若不是,请说明理由.
参考答案
1.C 2.A 3.C 4.C 5.0(答案不唯一)
7.【解】(1)根据题意,得解得(舍去).
∴二次函数的解析式为其图象如图所示.
(2)该函数图象的对称轴为y轴,顶点坐标为(0,0).
(3)∵点P(m,n)是此二次函数图象上的一点,且-2≤m≤1,
∴当m=-2时,
当m=1时,
当m=0时,n取最大值,n=0.
∴当-2≤m≤1时,-4≤n≤0.
8.D
9.B【点拨】设直线AB与y轴交于点E.∵直线y=2与二次函数交于A,B两点,∴当y=2时,得x=±,∴A(-,2),B(,2).∴AB=2.又∵CD=2AB,由二次函数图象的对称性可得CE=将点D的坐标代入y=ax ,得8a=2,解得
10.B【点拨】①抛物线顶点坐标为(0,0),故①说法正确,符合题意;②由题图可知,k>0,a>0,二次函数的顶点坐标为(0.0),所以当x>0时,直线y=kx+b(k≠0)与抛物线的函数值都随着x的增大而增大,故②说法正确,符合题意;③由点A的横坐标是-2,点B的横坐标是3,若AB=5,可得出直线AB与x轴平行,即k=0,与已知k≠0矛盾,故③说法错误,不符合题意;④当△OAB为等边三角形时,有OA=OB,可得出直线AB与x轴平行,即.k=0,与已知k≠0矛盾,故④说法错误,不符合题意;⑤由可知,所以判断直线y=kx+b(k≠0)的图象在抛物线的上方时,x的取值范围,结合两者交点A,B的横坐标可得,-2
12.【解】(1)存在一定点F,使得PM=PF恒成立.
过点P作PB⊥y轴于点B.
设点P的坐标为∴易知
又∵PB=a,∴在Rt△PBF中,.
∴OF=1.∴点F的坐标为(0,1).
(2)6【点拨】由(1),得PM=PF,∴QP+PF的最小值为QP+PM的最小值.∴当Q,P,M三点共线时,QP+PM有最小值,最小值为点Q的纵坐标加点M的纵坐标的绝对值.∴QP+PF的最小值为6.
13.【解】(1)(-3,-9),(1,-1)
(2)∵A,B是抛物线图象上的两点,
设A(m,-m ),B(n,-n ),则
当k>0时,如图①,
根据题意,得整理,得
易知m,n是的两个根,∴.
设直线y=kx-3与y轴的交点为D,则点D(0,-3),∴OD=3.
∵易知且S△NAB。n)(m-n),∴3=-2n×(m+n)=2nk,∴2nk=-mn.
又∵n≠0,∴m=-2k.∴n=k.∴-2k×k=-3,解得或(舍去),故
当k<0时,如图②,
根据题意,得整理,得
易知m,n是的两个根,∴m+n=-k,mn=-3.
设直线y=kx-3与y轴的交点为D,则点D(0,-3),∴OD=3,
∵易知m).∴3=2n×(m+n)=-2nk.∴-2nk=-mn.
又∵n≠0,∴m=2k.∴n=-3k.∴2k×(-3k)=-3,
解得或(舍去),故
综上所述,k的值为或
(3)直线AB'一定经过定点(0,3).
∵A,B是抛物线图象上的两点,
∴设A(m,-m ),B(n,-n ),则.
根据题意,得整理,得
易知m,n是的两个根,∴m+n=-k,mn=-3.设直线AB'的函数解析式为y=px+q,根据题意,得解得
∴直线AB'的函数解析式为.
∴直线AB'的函数解析式为.
∴直线.AB'一定经过定点(0,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
