14.3 角的平分线 第1课时 角的平分线的性质(含答案)
文档属性
| 名称 | 14.3 角的平分线 第1课时 角的平分线的性质(含答案) | 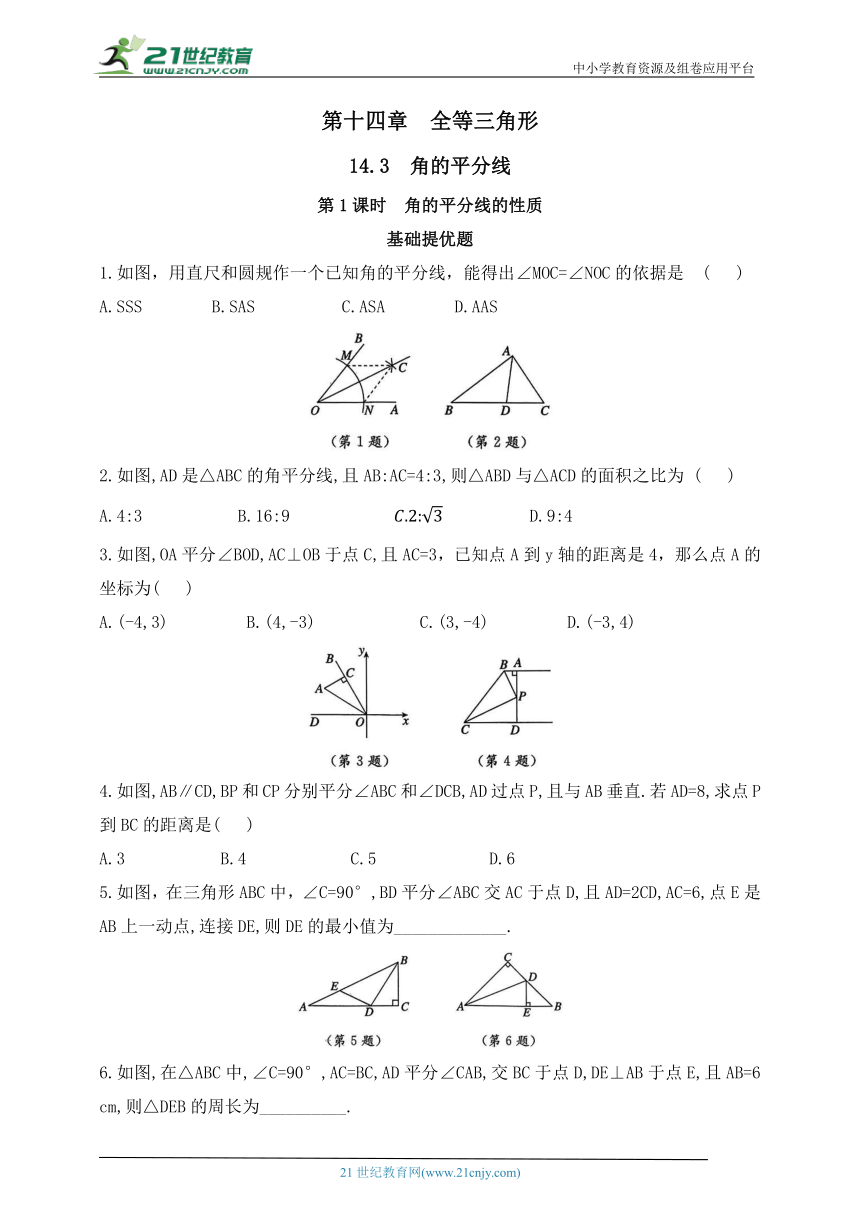 | |
| 格式 | docx | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 08:12:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十四章 全等三角形
14.3 角的平分线
第1课时 角的平分线的性质
基础提优题
1.如图,用直尺和圆规作一个已知角的平分线,能得出∠MOC=∠NOC的依据是 ( )
A.SSS B.SAS C.ASA D.AAS
2.如图,AD是△ABC的角平分线,且AB:AC=4:3,则△ABD与△ACD的面积之比为 ( )
A.4:3 B.16:9 D.9:4
3.如图,OA平分∠BOD,AC⊥OB于点C,且AC=3,已知点A到y轴的距离是4,那么点A的坐标为( )
A.(-4,3) B.(4,-3) C.(3,-4) D.(-3,4)
4.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,求点P到BC的距离是( )
A.3 B.4 C.5 D.6
5.如图,在三角形ABC中,∠C=90°,BD平分∠ABC交AC于点D,且AD=2CD,AC=6,点E是AB上一动点,连接DE,则DE的最小值为_____________.
6.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6cm,则△DEB的周长为__________.
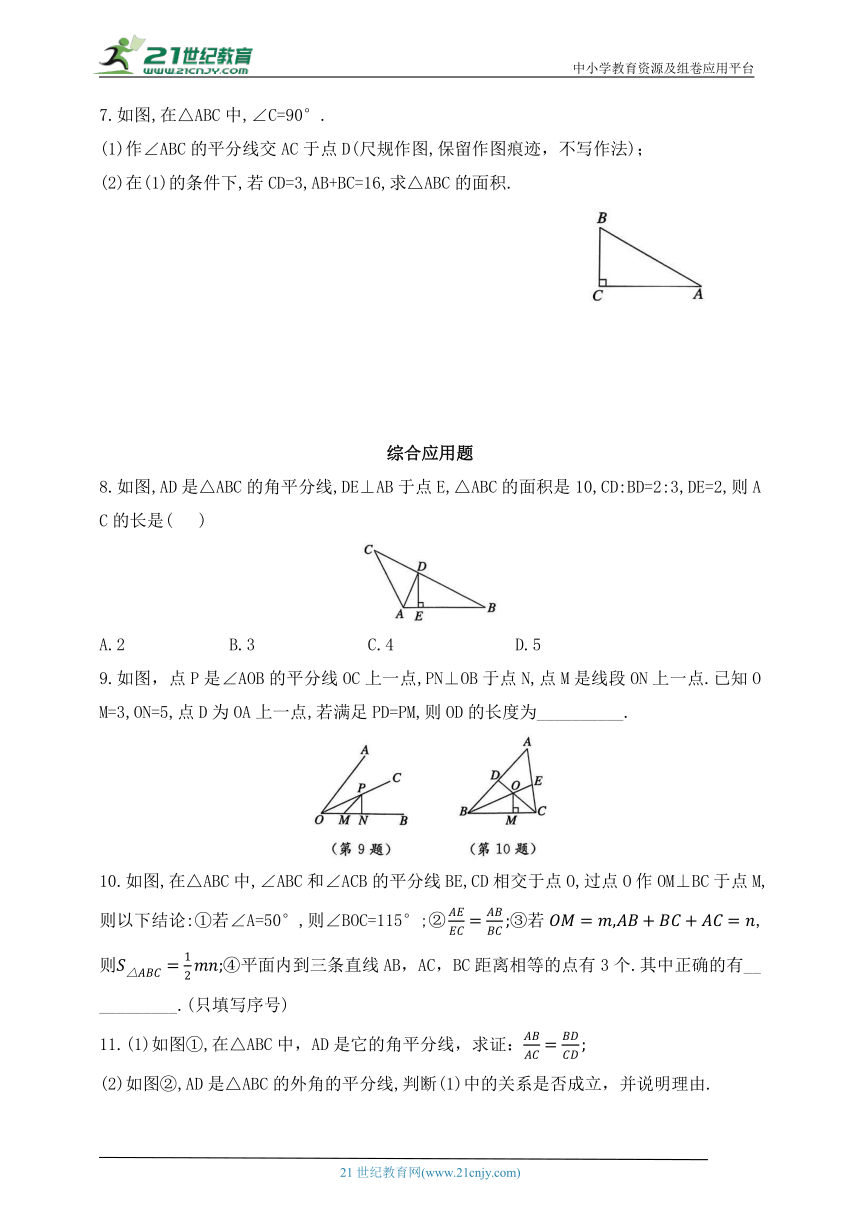
7.如图,在△ABC中,∠C=90°.
(1)作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,若CD=3,AB+BC=16,求△ABC的面积.
综合应用题
8.如图,AD是△ABC的角平分线,DE⊥AB于点E,△ABC的面积是10,CD:BD=2:3,DE=2,则AC的长是( )
A.2 B.3 C.4 D.5
9.如图,点P是∠AOB的平分线OC上一点,PN⊥OB于点N,点M是线段ON上一点.已知OM=3,ON=5,点D为OA上一点,若满足PD=PM,则OD的长度为__________.
10.如图,在△ABC中,∠ABC和∠ACB的平分线BE,CD相交于点O,过点O作OM⊥BC于点M,则以下结论:①若∠A=50°,则∠BOC=115°;③若,则④平面内到三条直线AB,AC,BC距离相等的点有3个.其中正确的有___________.(只填写序号)
11.(1)如图①,在△ABC中,AD是它的角平分线,求证:
(2)如图②,AD是△ABC的外角的平分线,判断(1)中的关系是否成立,并说明理由.
创新拓展题
12.【教材呈现】下面是人教版八年级上册数学教材49页的部分内容.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证PD=PE.
【问题解决】(1)请写出证明PD=PE的过程.
【类比探究】
(2)如图①,∠AOB=90°,OC是∠AOB的平分线,点M,N分别在OB,OA上,点P在射线OC上,连接PM和PN且PM⊥PN,求证:PM=PN.
(3)如图②,OC是∠AOB的平分线,点P在OC上,点M,N分别在OB,OA上,连接PM和PN,若∠PMO+∠PNO=180°,判断线段PM与PN的数量关系,并证明.
参考答案
1.A 2.A 3.A
4.B【点拨】过点P作PE⊥BC于E,∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.∵PA+PD=AD=8,∴PA=PD=4,∴PE=4.∴点P到BC的距离为4.
5.2【点拨】如图,当DE⊥AB时,DE有最小值.∵AD=2CD,平分∠ABC,DE⊥AB,DC⊥BC,∴DE=DC=2,∴DE的最小值为2.
6.6cm【点拨】∵AD平分∠CAB,∠C=90°,DE⊥AB,∴CD=DE,在Rt△ACD和Rt△AED中,∴Rt△ACD≌Rt△AED(HL),∴AC=AE,CD=ED,∴△DEB的周长为BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB.∵AB=6cm,∴△DEB的周长为6cm.
7.【解】(1)如图,BD即为∠ABC的平分线. 故③正确;
(2)如图,过点D作DH⊥AB于点H.
∵∠C=90°,∴DC⊥BC,
∵BD平分∠ABC,DH⊥AB,
∴DH=CD=3,
8.C【点拨】如图,过点D作DF⊥AC于F,∵AD是△ABC中∠BAC的角平分线,DE⊥AB,∴DF=DE=2.∵△ABC的面积是10,CD:BD=2:3,∴S△ADC=2=4,解得AC=4.
9.3或7
10.①②③【点拨】在△ABC中,若∠A=50°,则∠ABC+∠ACB=180°-∠A=180°-50°=130°.∵BE,CD分别平分∠ABC,∠ACB,∴∠ABE=∠CBE=在△BCO中,∠BOC=故①正确;
如图所示,过点E作EH⊥AB,EG⊥BC于点H,G,过点B作BK⊥AC于点K,
∵BE是∠ABC的平分线,故②正确;
如图所示,过点O作OR⊥AB,OS⊥AC于点R,S,连接OA,
∵BE,CD分别平分∠ABC,∠ACB,OM⊥BC,∴OM=OR=OS=m.∴S△ABC=故③正确;
∵OM=OR=OS,∴三角形内部有一个点O到直线AB,AC,BC距离相等,如图③所示,作△ABC外角的角平分线BP ,AP ,交于点P .过点P 作P N ⊥BC,P N ⊥AB,P N ⊥AC,
由角平分线的性质定理可得同理可得,三角形外部共有3个点到直线AB,AC,BC的距离相等,∴共有4个点到直线AB,AC,BC的距离相等,故④错误;综上所述,正确的有①②③.
11.(1)【证明】如图①,过点D作DE⊥AB于点E,DF⊥AC于点F,
∵AD平分∠BAC,∴DE=DF.
过点A作AH⊥BC于点H,
(2)【解】(1)中的关系仍然成立.理由如下:如图②,过点D作DF⊥AB于点F,DG⊥AC于点G,
∵AD平分∠CAE,∴DF=DG.
∵△ABD的面积△ACD的面积
过点A作AH⊥BD于点H,
12.(1)【证明】∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,∴∠POE=∠POD,∠OEP=∠ODP=90°.
在△OPE和△OPD中,∴△OPE≌△OPD(AAS),∴PD=PE.
(2)【证明】如图①,过点P分别作PE⊥OA于点E,PF⊥OB于点F,
∵OC是∠AOB的平分线,∴PE=PF,∠PEO=∠PFO=90°.
∠PFO=90°.
∵PM⊥PN,∴∠EPF=∠NPM,
∴∠EPF-∠EPM=∠NPM-∠EPM,即∠MPF=∠NPE.
在△PNE和△PMF中,∴△PNE≌△PMF(ASA).∴PM=PN.
(3)【解】PM=PN.
证明:如图②,过点P作PE⊥OA于点E,PF⊥OB于点F,
∵OC是∠AOB的平分线,∴PE=PF.
∵∠PNO+∠PNE=180°,∠PMO+∠PNO=180°,∴∠PNE=∠PMO.
在△PNE和△PMF中,∴△PNE≌△PMF(AAS),∴PM=PN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十四章 全等三角形
14.3 角的平分线
第1课时 角的平分线的性质
基础提优题
1.如图,用直尺和圆规作一个已知角的平分线,能得出∠MOC=∠NOC的依据是 ( )
A.SSS B.SAS C.ASA D.AAS
2.如图,AD是△ABC的角平分线,且AB:AC=4:3,则△ABD与△ACD的面积之比为 ( )
A.4:3 B.16:9 D.9:4
3.如图,OA平分∠BOD,AC⊥OB于点C,且AC=3,已知点A到y轴的距离是4,那么点A的坐标为( )
A.(-4,3) B.(4,-3) C.(3,-4) D.(-3,4)
4.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,求点P到BC的距离是( )
A.3 B.4 C.5 D.6
5.如图,在三角形ABC中,∠C=90°,BD平分∠ABC交AC于点D,且AD=2CD,AC=6,点E是AB上一动点,连接DE,则DE的最小值为_____________.
6.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6cm,则△DEB的周长为__________.
7.如图,在△ABC中,∠C=90°.
(1)作∠ABC的平分线交AC于点D(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,若CD=3,AB+BC=16,求△ABC的面积.
综合应用题
8.如图,AD是△ABC的角平分线,DE⊥AB于点E,△ABC的面积是10,CD:BD=2:3,DE=2,则AC的长是( )
A.2 B.3 C.4 D.5
9.如图,点P是∠AOB的平分线OC上一点,PN⊥OB于点N,点M是线段ON上一点.已知OM=3,ON=5,点D为OA上一点,若满足PD=PM,则OD的长度为__________.
10.如图,在△ABC中,∠ABC和∠ACB的平分线BE,CD相交于点O,过点O作OM⊥BC于点M,则以下结论:①若∠A=50°,则∠BOC=115°;③若,则④平面内到三条直线AB,AC,BC距离相等的点有3个.其中正确的有___________.(只填写序号)
11.(1)如图①,在△ABC中,AD是它的角平分线,求证:
(2)如图②,AD是△ABC的外角的平分线,判断(1)中的关系是否成立,并说明理由.
创新拓展题
12.【教材呈现】下面是人教版八年级上册数学教材49页的部分内容.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证PD=PE.
【问题解决】(1)请写出证明PD=PE的过程.
【类比探究】
(2)如图①,∠AOB=90°,OC是∠AOB的平分线,点M,N分别在OB,OA上,点P在射线OC上,连接PM和PN且PM⊥PN,求证:PM=PN.
(3)如图②,OC是∠AOB的平分线,点P在OC上,点M,N分别在OB,OA上,连接PM和PN,若∠PMO+∠PNO=180°,判断线段PM与PN的数量关系,并证明.
参考答案
1.A 2.A 3.A
4.B【点拨】过点P作PE⊥BC于E,∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD.∵PA+PD=AD=8,∴PA=PD=4,∴PE=4.∴点P到BC的距离为4.
5.2【点拨】如图,当DE⊥AB时,DE有最小值.∵AD=2CD,平分∠ABC,DE⊥AB,DC⊥BC,∴DE=DC=2,∴DE的最小值为2.
6.6cm【点拨】∵AD平分∠CAB,∠C=90°,DE⊥AB,∴CD=DE,在Rt△ACD和Rt△AED中,∴Rt△ACD≌Rt△AED(HL),∴AC=AE,CD=ED,∴△DEB的周长为BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB.∵AB=6cm,∴△DEB的周长为6cm.
7.【解】(1)如图,BD即为∠ABC的平分线. 故③正确;
(2)如图,过点D作DH⊥AB于点H.
∵∠C=90°,∴DC⊥BC,
∵BD平分∠ABC,DH⊥AB,
∴DH=CD=3,
8.C【点拨】如图,过点D作DF⊥AC于F,∵AD是△ABC中∠BAC的角平分线,DE⊥AB,∴DF=DE=2.∵△ABC的面积是10,CD:BD=2:3,∴S△ADC=2=4,解得AC=4.
9.3或7
10.①②③【点拨】在△ABC中,若∠A=50°,则∠ABC+∠ACB=180°-∠A=180°-50°=130°.∵BE,CD分别平分∠ABC,∠ACB,∴∠ABE=∠CBE=在△BCO中,∠BOC=故①正确;
如图所示,过点E作EH⊥AB,EG⊥BC于点H,G,过点B作BK⊥AC于点K,
∵BE是∠ABC的平分线,故②正确;
如图所示,过点O作OR⊥AB,OS⊥AC于点R,S,连接OA,
∵BE,CD分别平分∠ABC,∠ACB,OM⊥BC,∴OM=OR=OS=m.∴S△ABC=故③正确;
∵OM=OR=OS,∴三角形内部有一个点O到直线AB,AC,BC距离相等,如图③所示,作△ABC外角的角平分线BP ,AP ,交于点P .过点P 作P N ⊥BC,P N ⊥AB,P N ⊥AC,
由角平分线的性质定理可得同理可得,三角形外部共有3个点到直线AB,AC,BC的距离相等,∴共有4个点到直线AB,AC,BC的距离相等,故④错误;综上所述,正确的有①②③.
11.(1)【证明】如图①,过点D作DE⊥AB于点E,DF⊥AC于点F,
∵AD平分∠BAC,∴DE=DF.
过点A作AH⊥BC于点H,
(2)【解】(1)中的关系仍然成立.理由如下:如图②,过点D作DF⊥AB于点F,DG⊥AC于点G,
∵AD平分∠CAE,∴DF=DG.
∵△ABD的面积△ACD的面积
过点A作AH⊥BD于点H,
12.(1)【证明】∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,∴∠POE=∠POD,∠OEP=∠ODP=90°.
在△OPE和△OPD中,∴△OPE≌△OPD(AAS),∴PD=PE.
(2)【证明】如图①,过点P分别作PE⊥OA于点E,PF⊥OB于点F,
∵OC是∠AOB的平分线,∴PE=PF,∠PEO=∠PFO=90°.
∠PFO=90°.
∵PM⊥PN,∴∠EPF=∠NPM,
∴∠EPF-∠EPM=∠NPM-∠EPM,即∠MPF=∠NPE.
在△PNE和△PMF中,∴△PNE≌△PMF(ASA).∴PM=PN.
(3)【解】PM=PN.
证明:如图②,过点P作PE⊥OA于点E,PF⊥OB于点F,
∵OC是∠AOB的平分线,∴PE=PF.
∵∠PNO+∠PNE=180°,∠PMO+∠PNO=180°,∴∠PNE=∠PMO.
在△PNE和△PMF中,∴△PNE≌△PMF(AAS),∴PM=PN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
