4.3 相似多边形 教学设计(表格式)北师大版数学九年级上册
文档属性
| 名称 | 4.3 相似多边形 教学设计(表格式)北师大版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 166.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:28:27 | ||
图片预览



文档简介
3 相似多边形
课题 第3节 相似多边形 授课类型 新授课
授课人
教学内容 课本P86-87
教学目标 1.经历相似多边形概念的形成过程,了解相似多边形的含义。 2.在探索相似多边形本质特征的过程中,进一步发展学生观察、操作、归纳、类比等多方面的能力,提高学生的数学思维水平。
教学重难点 重点:会根据条件判断两个多边形是否为相似多边形。 难点:掌握相似多边形的性质,能根据相似比进行相关的计算。
教学准备 多媒体课件、量角器、直尺。
教与学互动设计(教学过程) 设计意图
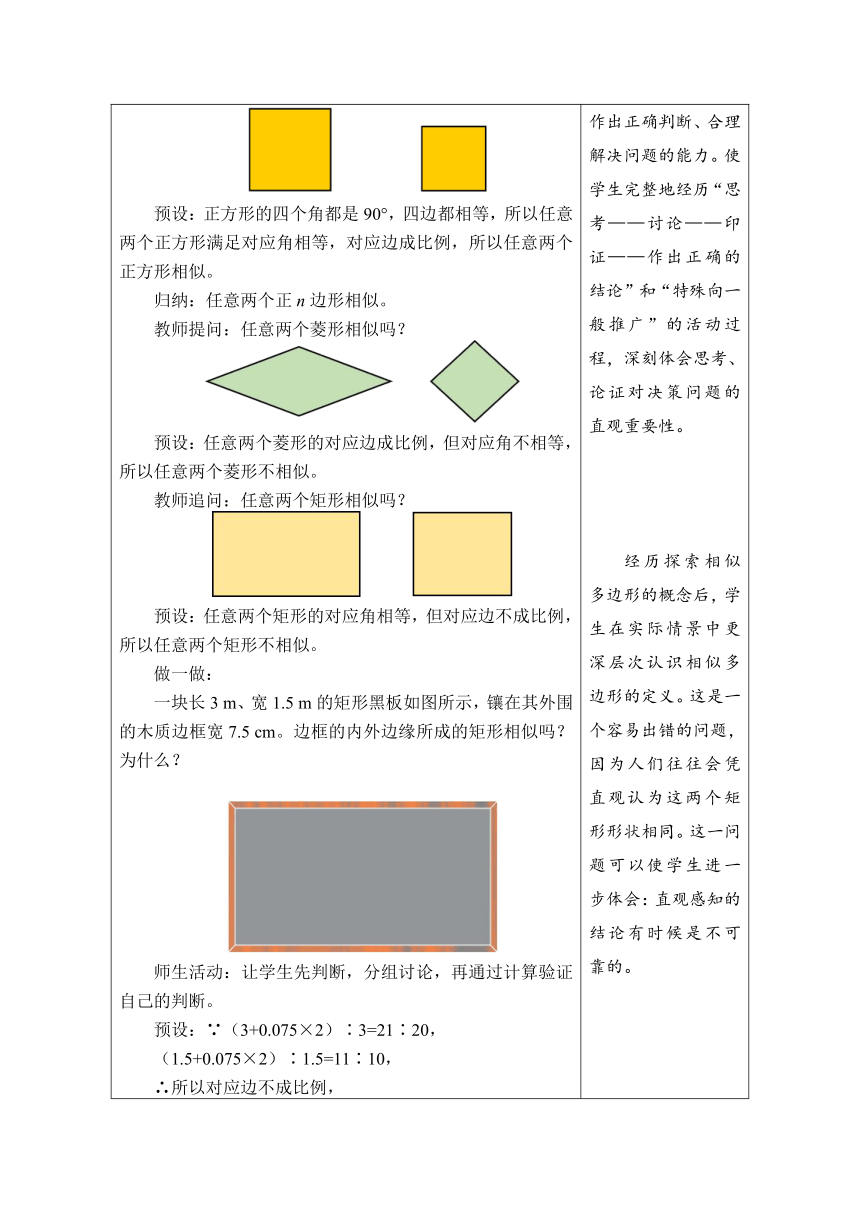
1.创设情景,导入新课 教师活动:教师在计算机上打开一张多边形图片,指着投影银幕问学生:计算机显示屏上的多边形与投影银幕上的多边形的形状相同吗? 学生回答:形状相同。 教师活动:以前我们学习过全等形,那这两个多边形有什么关系呢?这节课,我们来学习相似多边形。(教师板书课题: 第3节 相似多边形) 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
2.实践探究,学习新知 【探究1】 图中的六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的多边形。 (1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜想。 师生活动:学生根据生活经验和直观判断容易得出结论,应鼓励学生用自己的方法验证所得到的结论。例如,可以用量角器度量;还可以把两多边形画在透明纸上,然后剪下来把对应的角重叠在一起进行比较。 预设:A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E =∠E1,∠F=∠F1。 教师活动:这样的角我们称为对应角。 (2)在这两个多边形中,夹相等内角的两边否成比例? 师生活动:可以引导学生通过度量比较的方法获得结论。当然,度量会有误差,因此若条件允许,可以在学生实际度量的基础上,用多媒体课件进行演示,使学生对有关结论确信不疑。 预设:。 教师活动:这样的边我们称为对应边。 (3)在上述两问题中,你如何描述这些你所列的角和边的关系?以及相似多边形的定义是什么? 教师活动:鼓励学生用自己的话总结、小组交流展示。 【归纳总结】 六边形ABCDEF六边形A1B1C1D1E1F1是形状相同的 多边形,其中∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1对应相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1的比都相等,称为对应边。 相似多边形的定义:各角分别相等、各边成比例的两个多边形叫做相似多边形。 (相似多边形的定义,既是最基本、最重要的相似多边形的判定方法,也是最本质、最重要的相似多边形的性质) 六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1,“∽”读作“相似于”。 (教师要提醒学生注意:在用相似符号记两个多边形相似时,之所以把表示对应角顶点的字母写在对应的位置上,是因为这样可以一目了然地知道它们的对应角和对应边,可以类比全等形) 相似比:相似多边形对应边的比叫做相似比。例如,六边形ABCDEF∽六边形A1B1C1D1E1F1,对应边的比 ,因此六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为k1=,六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为k2=。 相似多边形的性质:相似多边形的对应角相等,对应边成比例。 【探究2】 想一想: 教师提问:任意两个等边三角形相似吗? 预设:等边三角形的三个角都是60°,三边都相等,所以任意两个等边三角形满足对应角相等,对应边成比例,所以任意两个等边三角形相似。 教师追问:任意两个正方形相似吗? 预设:正方形的四个角都是90°,四边都相等,所以任意两个正方形满足对应角相等,对应边成比例,所以任意两个正方形相似。 归纳:任意两个正n边形相似。 教师提问:任意两个菱形相似吗? 预设:任意两个菱形的对应边成比例,但对应角不相等,所以任意两个菱形不相似。 教师追问:任意两个矩形相似吗? 预设:任意两个矩形的对应角相等,但对应边不成比例,所以任意两个矩形不相似。 做一做: 一块长3 m、宽1.5 m的矩形黑板如图所示,镶在其外围的木质边框宽7.5 cm。边框的内外边缘所成的矩形相似吗?为什么? 师生活动:让学生先判断,分组讨论,再通过计算验证自己的判断。 预设:∵(3+0.075×2)∶3=21∶20, (1.5+0.075×2)∶1.5=11∶10, ∴所以对应边不成比例, ∴边框的内外边缘所成的不矩形相似。 【归纳总结】 任意两个正n边形相似。 任意两个菱形“各边成比例”,但不一定“各角分别相等”;矩形则正好相反:任意两个矩形“各角分别相等”,但不一定“各边成比例”。菱形和矩形从两个方面说明了,“各角分别相等”和“各边成比例”是刻画多边形相似的两个本质特征,二者缺一不可。 根据生活经验和直观判断,以问答的形式引导学生逐步深入的思考多边形相似的条件。问题的设置是帮助学生直观地寻找相似多边形特点;在前两个问题的铺设下,问题(3)的设置起到归纳总结的作用。 学生在教师的引导下总结相似多边形的定义。 判断两个正多边形的相似性,以及两个菱形的相似性,巩固对相似多边形概念的理解 此处留给学生充分的时间与空间去想象和思考。并培养学生对某个问题作出正确判断、合理解决问题的能力。使学生完整地经历“思考——讨论——印证——作出正确的结论”和“特殊向一般推广”的活动过程,深刻体会思考、论证对决策问题的直观重要性。 经历探索相似多边形的概念后,学生在实际情景中更深层次认识相似多边形的定义。这是一个容易出错的问题,因为人们往往会凭直观认为这两个矩形形状相同。这一问题可以使学生进一步体会:直观感知的结论有时候是不可靠的。
3.学以致用,应用新知 考点1 相似多边形的定义 例1 下面四个选项中的一般三角形、等边三角形、正方形、矩形的各边分别等距向外扩张1个单位,那么扩张后的几何图形与原几何图形不一定相似的是( ) A B C D 答案:D 变式训练 在如图所示的三个矩形中,相似的是( ) A. 甲和乙 B. 甲和丙 C. 乙和丙 D. 甲、乙和丙 答案:A 考点2 相似多边形的相似比及性质 例2 两个相似多边形一组对应边分别为3 cm,4.5 cm,那么它们的相似比为( ) A. 3∶2 B. 2∶3 C. 4∶9 D. 9∶4 答案:B 变式训练 如图所示的两个四边形相似,则下列结论不正确的是( ) A. a=2 B. m=2n C. x=2 D. ∠α=60° 答案:B 通过例题的讲解,巩固学生理解相似多边形的定义,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用相似多边形的相似比及性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 下列四组图形中,一定相似的是( ) A. 正方形与矩形 B. 正方形与菱形 C. 菱形与菱形 D. 正五边形与正五边形 答案:D 2. 如图所示的两个四边形相似,则α的度数是( ) A. 87° B. 60° C. 75° D. 120° 答案:A 3. 若△ABC∽△A′B′C′,且AB∶A′B′=1∶2,则△ABC与△A′B′C′相似比是_______,△A′B′C′与△ABC的相似比是_______。 答案: 6 4. 如图,把矩形ABCD对折,折痕为EF,若矩形ABCD与矩形EABF相似,AB=1。 (1)求BC的长; (2)求矩形ABEF与矩形ABCD的相似比。 解:(1)∵E是AD的中点, ∴AE=。 又∵矩形ABCD与矩形EABF相似,AB=1, ∴。 ∴AB2=AE·BC, 即12=BC·BC。 解得BC=。 (2)矩形ABEF与矩形ABCD的相似比===。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.相似多边形的定义 各角分别相等、各边成比例的两个多边形叫做相似多边形。 2.相似比 相似多边形对应边的比叫做相似比。 3.相似多边形的性质 相似多边形的对应角相等,对应边成比例。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P88习题4.4中的T1、T2、T3、T4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第3节 相似多边形 1.相似多边形的定义 2.相似比 3.相似多边形的性质 提纲掣领,重点突出。
教后反思 1.培养学生的主体意识,尊重学生的主体地位,让学生根据自己的理解,猜测、推断出结论,培养学生主动学习、自主探究的意识,真正成为课堂学习的主人。 2.根据学生的个体差异,注意因材施教、分层教学,在教学中结合课本“想一想”“议一议”“做一做”等教学环节调动学生的潜能,为每一位学生创设施展才能的空间,让学生学得轻松、愉快,增强学生的成就感,使每一位学生都能获得不同程度的成功。同时把学生的活动贯穿于教学的整体过程中,提供学生学习合作、交流、探索、归纳的机会,使学生最大限度的动手、动口、动脑、同伴互助,让学生通过实际感悟相似多边形的概念,找出相似多边形的性质。通过“读一读”让学生感受到数学的实际应用价值。 3.增加对学生自主探索的问题的拓展,应给学生充分时间和空间去自主学习,更加关心和爱护每一名学生,对需要指导的学生给予适当的指导.在教学方法和教学语言的选择上,尽可能注意知识的衔接,既不违反科学性,又符合可接受性原则,教师在课堂上要起好主导作用,并让学生有充分的活动机会,使得课堂气氛有新鲜感。对实现“人人学有价值的数学;人人都获得必需的数学;不同的人在数学上得到不同的发展”做得还不够。 反思,更进一步提升。
课题 第3节 相似多边形 授课类型 新授课
授课人
教学内容 课本P86-87
教学目标 1.经历相似多边形概念的形成过程,了解相似多边形的含义。 2.在探索相似多边形本质特征的过程中,进一步发展学生观察、操作、归纳、类比等多方面的能力,提高学生的数学思维水平。
教学重难点 重点:会根据条件判断两个多边形是否为相似多边形。 难点:掌握相似多边形的性质,能根据相似比进行相关的计算。
教学准备 多媒体课件、量角器、直尺。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 教师活动:教师在计算机上打开一张多边形图片,指着投影银幕问学生:计算机显示屏上的多边形与投影银幕上的多边形的形状相同吗? 学生回答:形状相同。 教师活动:以前我们学习过全等形,那这两个多边形有什么关系呢?这节课,我们来学习相似多边形。(教师板书课题: 第3节 相似多边形) 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
2.实践探究,学习新知 【探究1】 图中的六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的多边形。 (1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜想。 师生活动:学生根据生活经验和直观判断容易得出结论,应鼓励学生用自己的方法验证所得到的结论。例如,可以用量角器度量;还可以把两多边形画在透明纸上,然后剪下来把对应的角重叠在一起进行比较。 预设:A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E =∠E1,∠F=∠F1。 教师活动:这样的角我们称为对应角。 (2)在这两个多边形中,夹相等内角的两边否成比例? 师生活动:可以引导学生通过度量比较的方法获得结论。当然,度量会有误差,因此若条件允许,可以在学生实际度量的基础上,用多媒体课件进行演示,使学生对有关结论确信不疑。 预设:。 教师活动:这样的边我们称为对应边。 (3)在上述两问题中,你如何描述这些你所列的角和边的关系?以及相似多边形的定义是什么? 教师活动:鼓励学生用自己的话总结、小组交流展示。 【归纳总结】 六边形ABCDEF六边形A1B1C1D1E1F1是形状相同的 多边形,其中∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1对应相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1的比都相等,称为对应边。 相似多边形的定义:各角分别相等、各边成比例的两个多边形叫做相似多边形。 (相似多边形的定义,既是最基本、最重要的相似多边形的判定方法,也是最本质、最重要的相似多边形的性质) 六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1,“∽”读作“相似于”。 (教师要提醒学生注意:在用相似符号记两个多边形相似时,之所以把表示对应角顶点的字母写在对应的位置上,是因为这样可以一目了然地知道它们的对应角和对应边,可以类比全等形) 相似比:相似多边形对应边的比叫做相似比。例如,六边形ABCDEF∽六边形A1B1C1D1E1F1,对应边的比 ,因此六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为k1=,六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为k2=。 相似多边形的性质:相似多边形的对应角相等,对应边成比例。 【探究2】 想一想: 教师提问:任意两个等边三角形相似吗? 预设:等边三角形的三个角都是60°,三边都相等,所以任意两个等边三角形满足对应角相等,对应边成比例,所以任意两个等边三角形相似。 教师追问:任意两个正方形相似吗? 预设:正方形的四个角都是90°,四边都相等,所以任意两个正方形满足对应角相等,对应边成比例,所以任意两个正方形相似。 归纳:任意两个正n边形相似。 教师提问:任意两个菱形相似吗? 预设:任意两个菱形的对应边成比例,但对应角不相等,所以任意两个菱形不相似。 教师追问:任意两个矩形相似吗? 预设:任意两个矩形的对应角相等,但对应边不成比例,所以任意两个矩形不相似。 做一做: 一块长3 m、宽1.5 m的矩形黑板如图所示,镶在其外围的木质边框宽7.5 cm。边框的内外边缘所成的矩形相似吗?为什么? 师生活动:让学生先判断,分组讨论,再通过计算验证自己的判断。 预设:∵(3+0.075×2)∶3=21∶20, (1.5+0.075×2)∶1.5=11∶10, ∴所以对应边不成比例, ∴边框的内外边缘所成的不矩形相似。 【归纳总结】 任意两个正n边形相似。 任意两个菱形“各边成比例”,但不一定“各角分别相等”;矩形则正好相反:任意两个矩形“各角分别相等”,但不一定“各边成比例”。菱形和矩形从两个方面说明了,“各角分别相等”和“各边成比例”是刻画多边形相似的两个本质特征,二者缺一不可。 根据生活经验和直观判断,以问答的形式引导学生逐步深入的思考多边形相似的条件。问题的设置是帮助学生直观地寻找相似多边形特点;在前两个问题的铺设下,问题(3)的设置起到归纳总结的作用。 学生在教师的引导下总结相似多边形的定义。 判断两个正多边形的相似性,以及两个菱形的相似性,巩固对相似多边形概念的理解 此处留给学生充分的时间与空间去想象和思考。并培养学生对某个问题作出正确判断、合理解决问题的能力。使学生完整地经历“思考——讨论——印证——作出正确的结论”和“特殊向一般推广”的活动过程,深刻体会思考、论证对决策问题的直观重要性。 经历探索相似多边形的概念后,学生在实际情景中更深层次认识相似多边形的定义。这是一个容易出错的问题,因为人们往往会凭直观认为这两个矩形形状相同。这一问题可以使学生进一步体会:直观感知的结论有时候是不可靠的。
3.学以致用,应用新知 考点1 相似多边形的定义 例1 下面四个选项中的一般三角形、等边三角形、正方形、矩形的各边分别等距向外扩张1个单位,那么扩张后的几何图形与原几何图形不一定相似的是( ) A B C D 答案:D 变式训练 在如图所示的三个矩形中,相似的是( ) A. 甲和乙 B. 甲和丙 C. 乙和丙 D. 甲、乙和丙 答案:A 考点2 相似多边形的相似比及性质 例2 两个相似多边形一组对应边分别为3 cm,4.5 cm,那么它们的相似比为( ) A. 3∶2 B. 2∶3 C. 4∶9 D. 9∶4 答案:B 变式训练 如图所示的两个四边形相似,则下列结论不正确的是( ) A. a=2 B. m=2n C. x=2 D. ∠α=60° 答案:B 通过例题的讲解,巩固学生理解相似多边形的定义,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用相似多边形的相似比及性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 下列四组图形中,一定相似的是( ) A. 正方形与矩形 B. 正方形与菱形 C. 菱形与菱形 D. 正五边形与正五边形 答案:D 2. 如图所示的两个四边形相似,则α的度数是( ) A. 87° B. 60° C. 75° D. 120° 答案:A 3. 若△ABC∽△A′B′C′,且AB∶A′B′=1∶2,则△ABC与△A′B′C′相似比是_______,△A′B′C′与△ABC的相似比是_______。 答案: 6 4. 如图,把矩形ABCD对折,折痕为EF,若矩形ABCD与矩形EABF相似,AB=1。 (1)求BC的长; (2)求矩形ABEF与矩形ABCD的相似比。 解:(1)∵E是AD的中点, ∴AE=。 又∵矩形ABCD与矩形EABF相似,AB=1, ∴。 ∴AB2=AE·BC, 即12=BC·BC。 解得BC=。 (2)矩形ABEF与矩形ABCD的相似比===。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.相似多边形的定义 各角分别相等、各边成比例的两个多边形叫做相似多边形。 2.相似比 相似多边形对应边的比叫做相似比。 3.相似多边形的性质 相似多边形的对应角相等,对应边成比例。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P88习题4.4中的T1、T2、T3、T4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第3节 相似多边形 1.相似多边形的定义 2.相似比 3.相似多边形的性质 提纲掣领,重点突出。
教后反思 1.培养学生的主体意识,尊重学生的主体地位,让学生根据自己的理解,猜测、推断出结论,培养学生主动学习、自主探究的意识,真正成为课堂学习的主人。 2.根据学生的个体差异,注意因材施教、分层教学,在教学中结合课本“想一想”“议一议”“做一做”等教学环节调动学生的潜能,为每一位学生创设施展才能的空间,让学生学得轻松、愉快,增强学生的成就感,使每一位学生都能获得不同程度的成功。同时把学生的活动贯穿于教学的整体过程中,提供学生学习合作、交流、探索、归纳的机会,使学生最大限度的动手、动口、动脑、同伴互助,让学生通过实际感悟相似多边形的概念,找出相似多边形的性质。通过“读一读”让学生感受到数学的实际应用价值。 3.增加对学生自主探索的问题的拓展,应给学生充分时间和空间去自主学习,更加关心和爱护每一名学生,对需要指导的学生给予适当的指导.在教学方法和教学语言的选择上,尽可能注意知识的衔接,既不违反科学性,又符合可接受性原则,教师在课堂上要起好主导作用,并让学生有充分的活动机会,使得课堂气氛有新鲜感。对实现“人人学有价值的数学;人人都获得必需的数学;不同的人在数学上得到不同的发展”做得还不够。 反思,更进一步提升。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
