4.7 相似三角形的性质(第2课时)教学设计(表格式)北师大版数学九年级上册
文档属性
| 名称 | 4.7 相似三角形的性质(第2课时)教学设计(表格式)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:30:50 | ||
图片预览



文档简介
7 相似三角形的性质
课题 第2课时 相似三角形周长比、面积比的性质 授课类型 新授课
授课人
教学内容 课本P109-110
教学目标 1.掌握相似三角形的周长比、面积比与相似比的关系;并能灵活运用相似多边形的周长比、面积比与相似比的关系解决实际问题。 2.经历探索相似三角形性质的过程,进一步体验由特殊到一般的归纳思想和方法,感悟转化的思想,积累数学活动经验。
教学重难点 重点:理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方。 难点:掌握相似三角形的周长比、面积比在实际中的应用。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10 m2,CD长为4 m,BD长为6 m。 教师提问:同学们你们能计算出整个花坛△ABC的面积吗? 学生活动:学生可能会利用三角形面积公式先求出高,再利用上节课学习的相似三角形的性质来解题,教师应予以肯定。 教师活动:事实上,相似三角形的面积比与相似比存在一定的关系,这节课,我们来学习相似三角形周长比、面积比的性质。(教师板书课题: 第2课时 相似三角形周长比、面积比的性质) 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
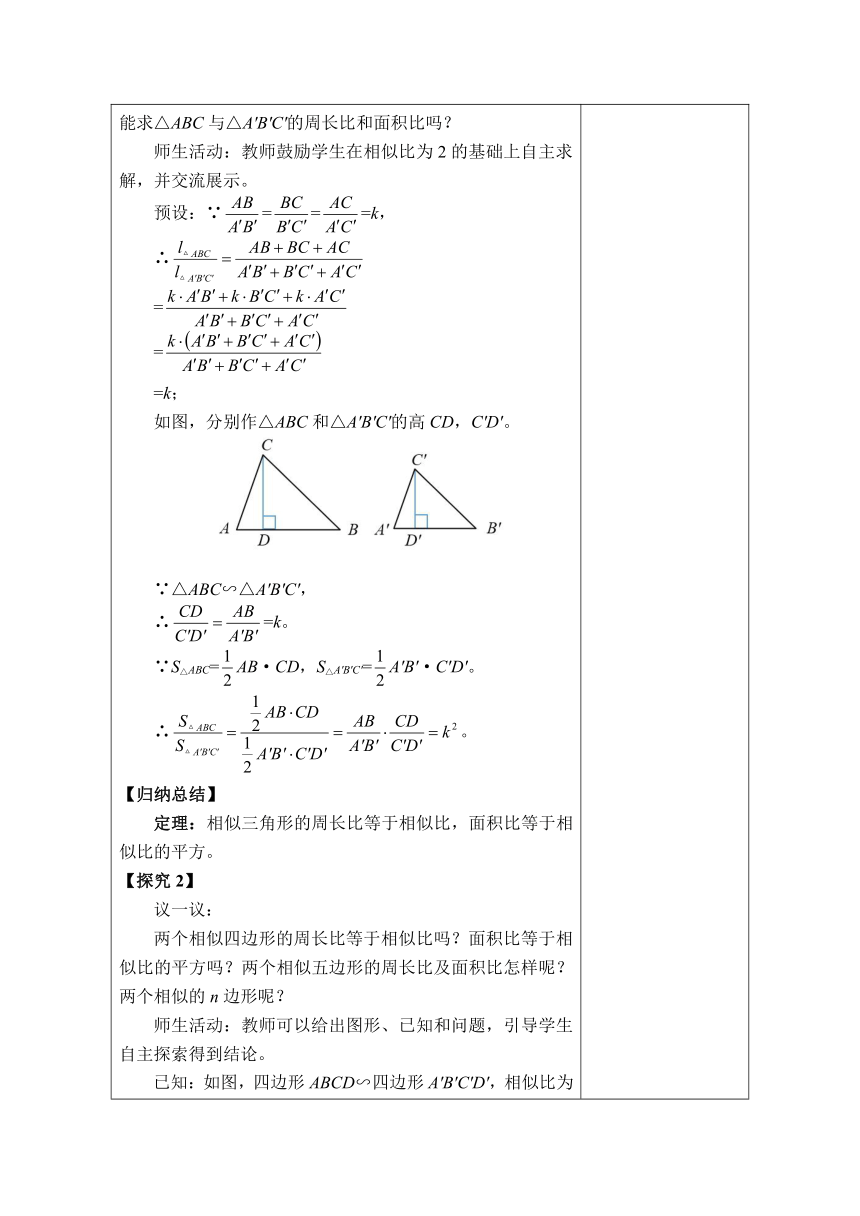
2.实践探究,学习新知 【探究1】 教师提问:如图,如果△ABC∽△A'B'C',相似比为2,那么△ABC与△A'B'C'的周长比是多少?面积比呢? 师生活动:教师鼓励学生自主解决,在求周长比时会用到笔记的等比性质,在求面积比时需要作出三角形的高,教师可在学生遇到困难时适当指导,并重视学生间的相互交流和启发。 预设:∵===2, ∴ = = =2; 如图,分别作△ABC和△A'B'C'的高CD,C′D′。 ∵△ABC∽△A'B'C', ∴=k(相似三角形对应高的比等于相似比)。 ∵S△ABC=AB·CD,S△A′B′C′=A′B′·C′D′。 ∴。 教师提问:如果△ABC∽△A'B'C',相似比为k,那么你能求△ABC与△A'B'C'的周长比和面积比吗? 师生活动:教师鼓励学生在相似比为2的基础上自主求解,并交流展示。 预设:∵===k, ∴ = = =k; 如图,分别作△ABC和△A'B'C'的高CD,C′D′。 ∵△ABC∽△A'B'C', ∴=k。 ∵S△ABC=AB·CD,S△A′B′C′=A′B′·C′D′。 ∴。 【归纳总结】 定理:相似三角形的周长比等于相似比,面积比等于相似比的平方。 【探究2】 议一议: 两个相似四边形的周长比等于相似比吗?面积比等于相似比的平方吗?两个相似五边形的周长比及面积比怎样呢?两个相似的n边形呢? 师生活动:教师可以给出图形、已知和问题,引导学生自主探索得到结论。 已知:如图,四边形ABCD∽四边形A′B′C′D′,相似比为k(k>0)。 (1)四边形ABCD与四边形A′B′C′D′的周长比是多少? (2)连接相应的对角线BD,B′D′,所得的△BCD与△B′C′D′相似吗?如果相似,它们的相似比各是多少?为什么? (3)设△ABD,△A′B′D′,△BCD,△B′C′D′的面积分别是,, , ,则,各是多少? (4)四边形ABCD与四边形A′B′C′D′的面积比是多少?如果把四边形换成五边形,那么结论又如何呢? 解:(1)∵四边形ABCD∽四边形A′B′C′D′相似比为k, ∴=k。 ∴。 (2)△BCD∽△B′C′D′,且相似比都为k。 ∵四边形ABCD∽四边形A′B′C′D′, ∴,∠C=∠C′。 在△BCD和△B′C′D′中, ∵,∠C=∠C′, ∴△BCD∽△B′C′D′。 ∴=k。 同理可知,△ABD∽△A′B′D′,且相似比为k。 (3)∵△ABD∽△A′B′D′, △BCD∽△B′C′D′, ∴=k2。 (4) =k2。 如果把四边形换成五边形,那么结论依旧成立。 总结:相似多边形的周长比等于相似比,面积比等于相似比的平方。 【教材例题】 例4 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半。已知BC=2,求△ABC平移的距离。 教师活动:操作投影仪。组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:根据题意,可知EG∥AB。 ∴∠GEC=∠B,∠EGC=∠A。 ∴△GEC∽△ABC(两角分别相等的两个三角形相似)。 ∴(相似三角形的面积比等于相似比的平方), 即。 ∴EC2=2。 ∴EC=(负值舍去)。 ∴BE=BC-EC=2-, 即△ABC平移的距离为2-。 学生通过计算相似比为2时,两个相似三角形的周长与面积比,积累在特殊相似比情况下,如何求解周长比和面积比的经验,为猜想并尝试推导一般情况下(相似比为k)周长比和面积比做铺垫。由此让学生感悟由特殊到一般的归纳思想和方法,体会类比的数学思想方法。 引导学生发现,无论是三角形、四边形,还是多边形,都有相同的结论,相似多边形的周长比等于相似比,面积比等于相似比的平方。学生亲身经历问题发现的过程,对知识从初步印象上升到了理论探求、证明的高度,今后在记忆和应用上会更加深刻。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。
3.学以致用,应用新知 考点1 相似三角形的周长比 例1 如图,△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△ABC与△DEF的周长比为( ) A. 1∶ B. 1∶2 C. 1∶3 D. 1∶4 答案:A 变式训练 两个相似三角形的最短边分别为5 cm和3 cm,它们的周长之差为14 cm,那么小三角形的周长为( ) A. 15 cm B. 17 cm C. 19 cm D. 21 cm 答案:D 考点2 相似三角形的面积比 例2 如图,△ABC是一块花园,D,E分别为线段BC,BA的中点,△EBD内种植的是太阳花,四边形AEDC内种植薰衣草。设整个花园的面积为S1,种植太阳花区域的面积为S2,则=( ) A. B. C. D. 答案:B 变式训练 两个相似三角形的面积之比是4∶9,其中一个三角形的周长为24 cm,则另一个三角形的周长是( ) A. 16 cm B. 16 cm或28 cm C. 36 cm D. 16 cm或36 cm 答案:D 通过例题的讲解,巩固学生应用相似三角形的周长比,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用相似三角形的面积比,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 如图,△ABO∽△CDO,BO=2OD,△CDO的周长为4,则△ABO的周长为( ) A. 2 B. 4 C. 8 D. 16 答案:C 2. 如图,在4×4的正方形网格中,△ABC的最短边长为,△MNG与△ABC相似,且其最短边长为2,则△MNG的面积为 ( ) A. 5 B. 5.5 C. 6 D. 6.5 答案:A 3. 两个相似三角形对应的中线长分别是6 cm和18 cm,若较大三角形的周长是42 cm,面积是12 cm2,则较小三角形的周长_______cm,面积为_______cm2。 答案:14 4. 如图,在△ABC中,AB=5,D是AB上的一点,AD=2,DE BC,交AC于点E,则△DEC与△ABC的面积比为_______。 答案:6∶25 5. 如图,在△ABC中,点D,E分别在边AB,AC上,DC与BE相交于点O,且DO=2,BO=DC=6,OE=3。 (1)求证:DE BC; (2)如果四边形BCED的面积比△ADE的面积大12,求△ABC的面积。 解:(1)∵OD=2,DC=6,OE=3, ∴OC=4,,。 ∴。 ∵∠DOE=∠BOC, ∴△DOE∽△COB。 ∴∠ODE=∠OCB, ∴DE∥BC。 (2)∵DE∥BC, ∴∠ADE=∠ABC,∠AED=∠ACB。 ∴△ADE∽△ABC。 ∴。 设△ADE的面积为x,则△ABC的面积为4x, ∴四边形BCED的面积为3x。 由题意得,3x-x=2x=12, 解得x=6。 ∴S△ABC=4x=24。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.相似三角形的周长比、面积比的性质 相似三角形的周长比等于相似比,面积比等于相似比的平方。 2.相似多边形的周长比、面积比的性质 相似多边形的周长比等于相似比,面积比等于相似比的平方。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P110-112习题4.12中的T1、T2、T3、T4、T5。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第2课时 相似三角形周长比、面积比的性质 1.相似三角形的周长比 2.相似三角形的面积比 3.相似多边形的周长比、面积比 提纲掣领,重点突出。
教后反思 经历相似三角形的性质的探索过程,培养学生的探索能力。通过交流、归纳,总结相似三角形的周长比、面积比与相似比的关系,体验化归思想。运用相似多边形的周长比,面积比解决实际问题,训练学生的运用能力,增强学生对知识的应用意识。 反思,更进一步提升。
课题 第2课时 相似三角形周长比、面积比的性质 授课类型 新授课
授课人
教学内容 课本P109-110
教学目标 1.掌握相似三角形的周长比、面积比与相似比的关系;并能灵活运用相似多边形的周长比、面积比与相似比的关系解决实际问题。 2.经历探索相似三角形性质的过程,进一步体验由特殊到一般的归纳思想和方法,感悟转化的思想,积累数学活动经验。
教学重难点 重点:理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方。 难点:掌握相似三角形的周长比、面积比在实际中的应用。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图所示是一个三角形的花坛,要在上面种满花草,园丁沿与AB平行的方向画一条直线,将花坛分割出一片三角形地块,测出△CDE的面积为10 m2,CD长为4 m,BD长为6 m。 教师提问:同学们你们能计算出整个花坛△ABC的面积吗? 学生活动:学生可能会利用三角形面积公式先求出高,再利用上节课学习的相似三角形的性质来解题,教师应予以肯定。 教师活动:事实上,相似三角形的面积比与相似比存在一定的关系,这节课,我们来学习相似三角形周长比、面积比的性质。(教师板书课题: 第2课时 相似三角形周长比、面积比的性质) 教师通过学生熟悉的场景和事物引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透善于观察生活中的数学的学习意识,同时也激发了学生的学习兴趣,加强了非智力因素的培养。
2.实践探究,学习新知 【探究1】 教师提问:如图,如果△ABC∽△A'B'C',相似比为2,那么△ABC与△A'B'C'的周长比是多少?面积比呢? 师生活动:教师鼓励学生自主解决,在求周长比时会用到笔记的等比性质,在求面积比时需要作出三角形的高,教师可在学生遇到困难时适当指导,并重视学生间的相互交流和启发。 预设:∵===2, ∴ = = =2; 如图,分别作△ABC和△A'B'C'的高CD,C′D′。 ∵△ABC∽△A'B'C', ∴=k(相似三角形对应高的比等于相似比)。 ∵S△ABC=AB·CD,S△A′B′C′=A′B′·C′D′。 ∴。 教师提问:如果△ABC∽△A'B'C',相似比为k,那么你能求△ABC与△A'B'C'的周长比和面积比吗? 师生活动:教师鼓励学生在相似比为2的基础上自主求解,并交流展示。 预设:∵===k, ∴ = = =k; 如图,分别作△ABC和△A'B'C'的高CD,C′D′。 ∵△ABC∽△A'B'C', ∴=k。 ∵S△ABC=AB·CD,S△A′B′C′=A′B′·C′D′。 ∴。 【归纳总结】 定理:相似三角形的周长比等于相似比,面积比等于相似比的平方。 【探究2】 议一议: 两个相似四边形的周长比等于相似比吗?面积比等于相似比的平方吗?两个相似五边形的周长比及面积比怎样呢?两个相似的n边形呢? 师生活动:教师可以给出图形、已知和问题,引导学生自主探索得到结论。 已知:如图,四边形ABCD∽四边形A′B′C′D′,相似比为k(k>0)。 (1)四边形ABCD与四边形A′B′C′D′的周长比是多少? (2)连接相应的对角线BD,B′D′,所得的△BCD与△B′C′D′相似吗?如果相似,它们的相似比各是多少?为什么? (3)设△ABD,△A′B′D′,△BCD,△B′C′D′的面积分别是,, , ,则,各是多少? (4)四边形ABCD与四边形A′B′C′D′的面积比是多少?如果把四边形换成五边形,那么结论又如何呢? 解:(1)∵四边形ABCD∽四边形A′B′C′D′相似比为k, ∴=k。 ∴。 (2)△BCD∽△B′C′D′,且相似比都为k。 ∵四边形ABCD∽四边形A′B′C′D′, ∴,∠C=∠C′。 在△BCD和△B′C′D′中, ∵,∠C=∠C′, ∴△BCD∽△B′C′D′。 ∴=k。 同理可知,△ABD∽△A′B′D′,且相似比为k。 (3)∵△ABD∽△A′B′D′, △BCD∽△B′C′D′, ∴=k2。 (4) =k2。 如果把四边形换成五边形,那么结论依旧成立。 总结:相似多边形的周长比等于相似比,面积比等于相似比的平方。 【教材例题】 例4 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半。已知BC=2,求△ABC平移的距离。 教师活动:操作投影仪。组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:根据题意,可知EG∥AB。 ∴∠GEC=∠B,∠EGC=∠A。 ∴△GEC∽△ABC(两角分别相等的两个三角形相似)。 ∴(相似三角形的面积比等于相似比的平方), 即。 ∴EC2=2。 ∴EC=(负值舍去)。 ∴BE=BC-EC=2-, 即△ABC平移的距离为2-。 学生通过计算相似比为2时,两个相似三角形的周长与面积比,积累在特殊相似比情况下,如何求解周长比和面积比的经验,为猜想并尝试推导一般情况下(相似比为k)周长比和面积比做铺垫。由此让学生感悟由特殊到一般的归纳思想和方法,体会类比的数学思想方法。 引导学生发现,无论是三角形、四边形,还是多边形,都有相同的结论,相似多边形的周长比等于相似比,面积比等于相似比的平方。学生亲身经历问题发现的过程,对知识从初步印象上升到了理论探求、证明的高度,今后在记忆和应用上会更加深刻。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。
3.学以致用,应用新知 考点1 相似三角形的周长比 例1 如图,△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△ABC与△DEF的周长比为( ) A. 1∶ B. 1∶2 C. 1∶3 D. 1∶4 答案:A 变式训练 两个相似三角形的最短边分别为5 cm和3 cm,它们的周长之差为14 cm,那么小三角形的周长为( ) A. 15 cm B. 17 cm C. 19 cm D. 21 cm 答案:D 考点2 相似三角形的面积比 例2 如图,△ABC是一块花园,D,E分别为线段BC,BA的中点,△EBD内种植的是太阳花,四边形AEDC内种植薰衣草。设整个花园的面积为S1,种植太阳花区域的面积为S2,则=( ) A. B. C. D. 答案:B 变式训练 两个相似三角形的面积之比是4∶9,其中一个三角形的周长为24 cm,则另一个三角形的周长是( ) A. 16 cm B. 16 cm或28 cm C. 36 cm D. 16 cm或36 cm 答案:D 通过例题的讲解,巩固学生应用相似三角形的周长比,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用相似三角形的面积比,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. 如图,△ABO∽△CDO,BO=2OD,△CDO的周长为4,则△ABO的周长为( ) A. 2 B. 4 C. 8 D. 16 答案:C 2. 如图,在4×4的正方形网格中,△ABC的最短边长为,△MNG与△ABC相似,且其最短边长为2,则△MNG的面积为 ( ) A. 5 B. 5.5 C. 6 D. 6.5 答案:A 3. 两个相似三角形对应的中线长分别是6 cm和18 cm,若较大三角形的周长是42 cm,面积是12 cm2,则较小三角形的周长_______cm,面积为_______cm2。 答案:14 4. 如图,在△ABC中,AB=5,D是AB上的一点,AD=2,DE BC,交AC于点E,则△DEC与△ABC的面积比为_______。 答案:6∶25 5. 如图,在△ABC中,点D,E分别在边AB,AC上,DC与BE相交于点O,且DO=2,BO=DC=6,OE=3。 (1)求证:DE BC; (2)如果四边形BCED的面积比△ADE的面积大12,求△ABC的面积。 解:(1)∵OD=2,DC=6,OE=3, ∴OC=4,,。 ∴。 ∵∠DOE=∠BOC, ∴△DOE∽△COB。 ∴∠ODE=∠OCB, ∴DE∥BC。 (2)∵DE∥BC, ∴∠ADE=∠ABC,∠AED=∠ACB。 ∴△ADE∽△ABC。 ∴。 设△ADE的面积为x,则△ABC的面积为4x, ∴四边形BCED的面积为3x。 由题意得,3x-x=2x=12, 解得x=6。 ∴S△ABC=4x=24。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.相似三角形的周长比、面积比的性质 相似三角形的周长比等于相似比,面积比等于相似比的平方。 2.相似多边形的周长比、面积比的性质 相似多边形的周长比等于相似比,面积比等于相似比的平方。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P110-112习题4.12中的T1、T2、T3、T4、T5。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第2课时 相似三角形周长比、面积比的性质 1.相似三角形的周长比 2.相似三角形的面积比 3.相似多边形的周长比、面积比 提纲掣领,重点突出。
教后反思 经历相似三角形的性质的探索过程,培养学生的探索能力。通过交流、归纳,总结相似三角形的周长比、面积比与相似比的关系,体验化归思想。运用相似多边形的周长比,面积比解决实际问题,训练学生的运用能力,增强学生对知识的应用意识。 反思,更进一步提升。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
