4.8 图形的位似(第1课时)教学设计(表格式)北师大版数学九年级上册
文档属性
| 名称 | 4.8 图形的位似(第1课时)教学设计(表格式)北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 613.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:31:08 | ||
图片预览

文档简介
8 图形的位似
课题 第1课时 图形的位似 授课类型 新授课
授课人
教学内容 课本P113-114
教学目标 1.理解位似多边形的有关概念;能利用位似将一个图形放大或缩小。 2.理解相似多边形与位似多边形的联系与区别。 3.掌握判断两个多边形是否是位似多边形的方法,并能准确指出位似中心和相似比。
教学重难点 重点:位似多边形的相关定义、性质的理解,绘制位似多边形方法的掌握。 难点:位似多边形的判断,从位似中心的不同方向绘制位似多边形。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图,是一幅宣传海报,它由一组形状相同的图片组成。 教师提问:在图片①和图片②上任取一组对应点A,A′,同学们你们能发现什么?自己动手试一试。 学生活动:学生通过连线、测量可以发现:直线AA′都经过镜头中心点O,且都等于一个固定值。 这节课,我们来学习图形的位似。(教师板书课题: 第1课时 图形的位似) 通过一个宣传海报的问题情境,让学生初步直观感受位似图形的特点。
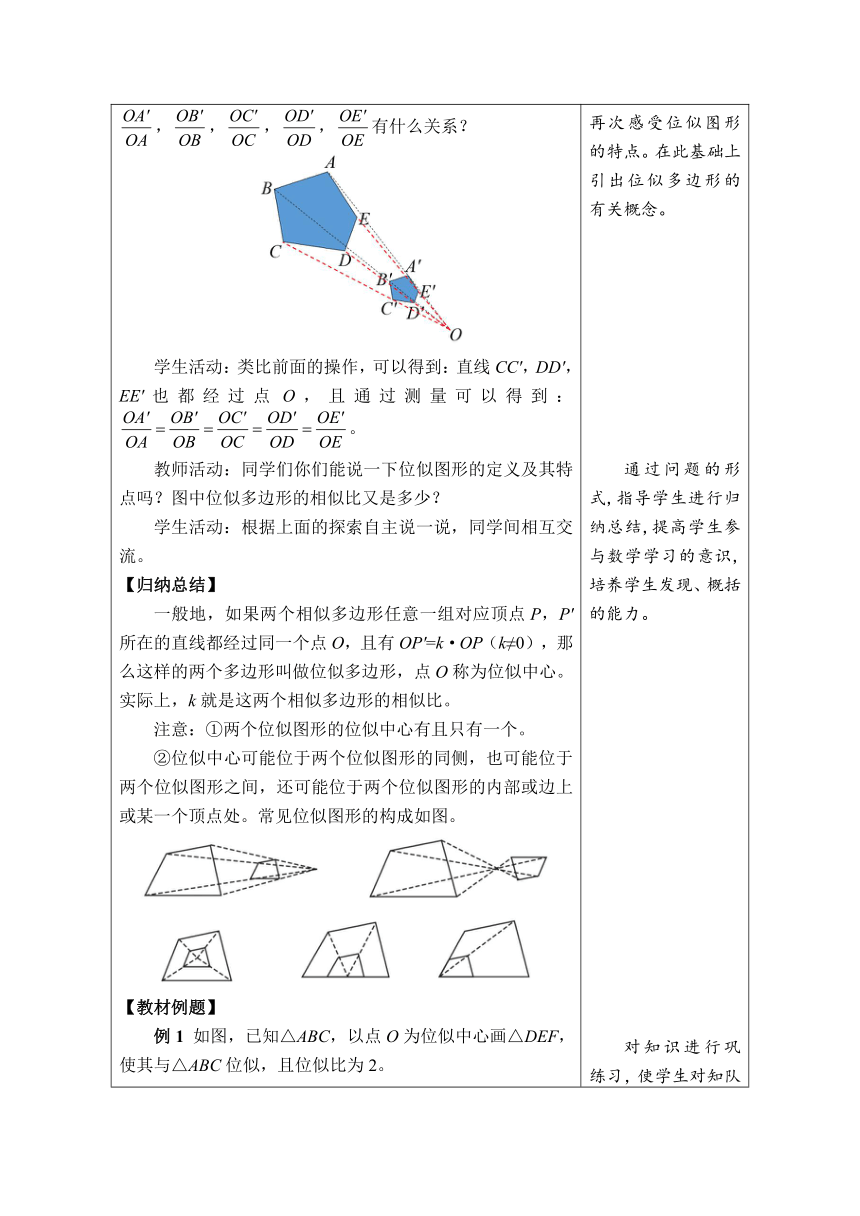
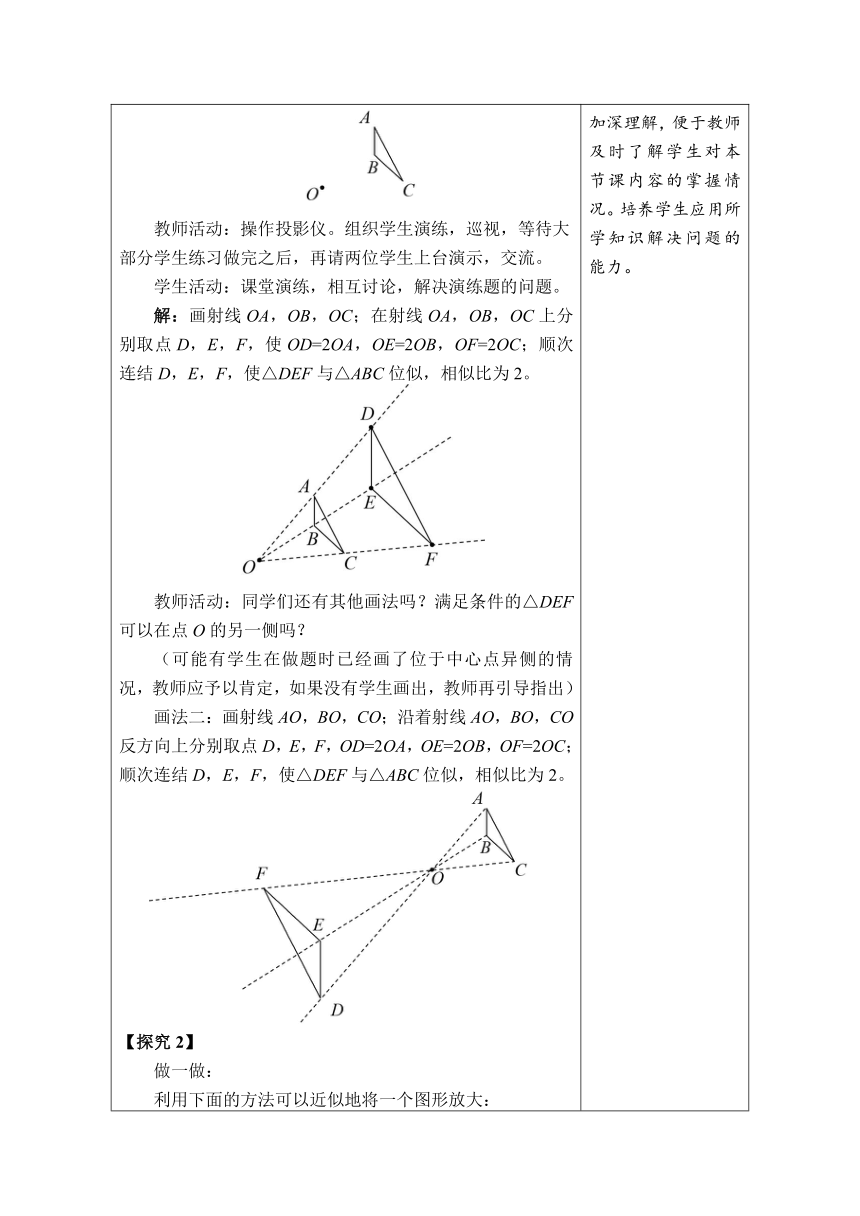
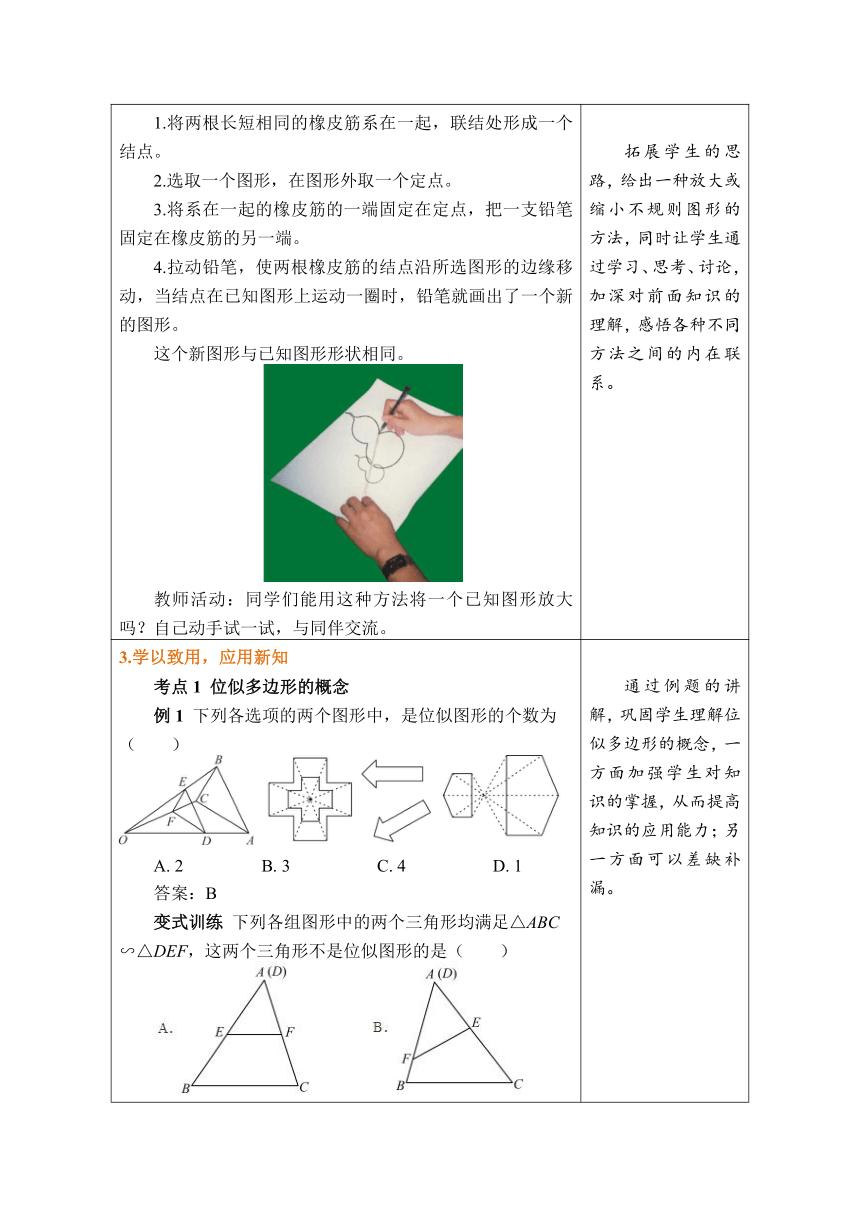
2.实践探究,学习新知 【探究1】 教师活动:如图是两个相似五边形,设直线AA′与BB′相交于点O,那么直线CC′,DD′,EE′是否也都经过点O?,,,,有什么关系? 学生活动:类比前面的操作,可以得到:直线CC′,DD′,EE′也都经过点O,且通过测量可以得到:。 教师活动:同学们你们能说一下位似图形的定义及其特点吗?图中位似多边形的相似比又是多少? 学生活动:根据上面的探索自主说一说,同学间相互交流。 【归纳总结】 一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一个点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O称为位似中心。实际上,k就是这两个相似多边形的相似比。 注意:①两个位似图形的位似中心有且只有一个。 ②位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处。常见位似图形的构成如图。 【教材例题】 例1 如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2。 教师活动:操作投影仪。组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC;顺次连结D,E,F,使△DEF与△ABC位似,相似比为2。 教师活动:同学们还有其他画法吗?满足条件的△DEF可以在点O的另一侧吗? (可能有学生在做题时已经画了位于中心点异侧的情况,教师应予以肯定,如果没有学生画出,教师再引导指出) 画法二:画射线AO,BO,CO;沿着射线AO,BO,CO反方向上分别取点D,E,F,OD=2OA,OE=2OB,OF=2OC;顺次连结D,E,F,使△DEF与△ABC位似,相似比为2。 【探究2】 做一做: 利用下面的方法可以近似地将一个图形放大: 1.将两根长短相同的橡皮筋系在一起,联结处形成一个结点。 2.选取一个图形,在图形外取一个定点。 3.将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端。 4.拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘移动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形。 这个新图形与已知图形形状相同。 教师活动:同学们能用这种方法将一个已知图形放大吗?自己动手试一试,与同伴交流。 呈现了两个具有特殊位置关系的相似五边形,让学生再次感受位似图形的特点。在此基础上引出位似多边形的有关概念。 通过问题的形式,指导学生进行归纳总结,提高学生参与数学学习的意识,培养学生发现、概括的能力。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。 拓展学生的思路,给出一种放大或缩小不规则图形的方法,同时让学生通过学习、思考、讨论,加深对前面知识的理解,感悟各种不同方法之间的内在联系。
3.学以致用,应用新知 考点1 位似多边形的概念 例1 下列各选项的两个图形中,是位似图形的个数为( ) A. 2 B. 3 C. 4 D. 1 答案:B 变式训练 下列各组图形中的两个三角形均满足△ABC∽△DEF,这两个三角形不是位似图形的是( ) 答案:B 考点2 位似多边形的性质 例2 如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=3OB,则△ABC与△DEF的周长之比是( ) A. 1∶2 B. 1∶4 C. 1∶3 D. 1∶9 答案:C 变式训练 如图,以点O为位似中心,把△ABC放大到原来的2倍得到△A′B′C′,以下说法中错误的是( ) A. △ABC∽△A′B′C′ B. 点A,O,A′三点在同一条直线上 C. AO∶AA′ D. S△ABC∶S△A′B′C′=1∶4 答案:C 考点3 位似多边形的画法 例3 课堂上数学老师让同学们完成“以点O为位似中心,将△ABC扩大到原来的两倍得到△A′B′C′,画出一个符合条件的△A′B′C′”的作图题,小明和小刚率先完成,他们的作图如下,则( ) A. 小明正确,小刚错误 B. 小明错误,小刚正确 C. 两人的作图都正确 D. 两人的作图都错误 答案:C 变式训练 如图,△ABC的顶点和定点O都在单位长度为1的正方形网格的格点上。以点O为位似中心,在网格纸中画出△ABC的位似△A′B′C′,使它与△ABC的相似比为2,且位于点O的右侧。 解: 通过例题的讲解,巩固学生理解位似多边形的概念,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用位似多边形的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生掌握位似多边形的画法,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. “标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形( ) A. 左上 B. 左下 C. 右上 D. 右下 答案:B 2. 如图,位似图形由三角尺与其灯光照射下的影子组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为( ) A. 8 cm B. 20 cm C. 3.2 cm D. 10 cm 答案:B 3. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( ) A. 1∶2 B. 1∶4 C. 1∶5 D. 1∶6 答案:B 4. 用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可选在( ) A. 原图形的外部 B. 原图形的内部 C. 原图形的边上 D. 任意位置 答案:D 5. 如图所示,△ABC与△A′B′C′关于点O位似,BO=3,B′O=6。 (1)若AC=5,求A′C′的长; (2)若△ABC的面积为7,求△A′B′C′的面积。 解:(1)∵△ABC与△A′B′C′是位似图形,位似比为OB∶OB′=3∶6=1∶2, ∴=,即=, ∴A′C′=10。 (2)根据题意,得==, 即=,所以S△A′B′C′=7×4=28。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一个点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O称为位似中心。实际上,k就是这两个相似多边形的相似比。 2.两个位似图形的位似中心有且只有一个;位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处。 3.位似多边形的画法 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P115习题4.13中的T1、T2、T3、T4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 图形的位似 1.位似多边形的概念及其性质 2.位似多边形的画法 提纲掣领,重点突出。
教后反思 位似是相似图形的延伸和深化。经历位似图形的探索过程,进一步发展学生的探究、交流能力,培养学生动手操作的能力,体验学习的乐趣.位似图形在实际生产和生活中有着广泛的应用,通过现实情境,进一步发展学生从数学角度提出问题、分析问题、解决问题的能力,培养学生的数学应用意识,体会数学与自然、社会的联系。 反思,更进一步提升。
课题 第1课时 图形的位似 授课类型 新授课
授课人
教学内容 课本P113-114
教学目标 1.理解位似多边形的有关概念;能利用位似将一个图形放大或缩小。 2.理解相似多边形与位似多边形的联系与区别。 3.掌握判断两个多边形是否是位似多边形的方法,并能准确指出位似中心和相似比。
教学重难点 重点:位似多边形的相关定义、性质的理解,绘制位似多边形方法的掌握。 难点:位似多边形的判断,从位似中心的不同方向绘制位似多边形。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图,是一幅宣传海报,它由一组形状相同的图片组成。 教师提问:在图片①和图片②上任取一组对应点A,A′,同学们你们能发现什么?自己动手试一试。 学生活动:学生通过连线、测量可以发现:直线AA′都经过镜头中心点O,且都等于一个固定值。 这节课,我们来学习图形的位似。(教师板书课题: 第1课时 图形的位似) 通过一个宣传海报的问题情境,让学生初步直观感受位似图形的特点。
2.实践探究,学习新知 【探究1】 教师活动:如图是两个相似五边形,设直线AA′与BB′相交于点O,那么直线CC′,DD′,EE′是否也都经过点O?,,,,有什么关系? 学生活动:类比前面的操作,可以得到:直线CC′,DD′,EE′也都经过点O,且通过测量可以得到:。 教师活动:同学们你们能说一下位似图形的定义及其特点吗?图中位似多边形的相似比又是多少? 学生活动:根据上面的探索自主说一说,同学间相互交流。 【归纳总结】 一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一个点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O称为位似中心。实际上,k就是这两个相似多边形的相似比。 注意:①两个位似图形的位似中心有且只有一个。 ②位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处。常见位似图形的构成如图。 【教材例题】 例1 如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2。 教师活动:操作投影仪。组织学生演练,巡视,等待大部分学生练习做完之后,再请两位学生上台演示,交流。 学生活动:课堂演练,相互讨论,解决演练题的问题。 解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC;顺次连结D,E,F,使△DEF与△ABC位似,相似比为2。 教师活动:同学们还有其他画法吗?满足条件的△DEF可以在点O的另一侧吗? (可能有学生在做题时已经画了位于中心点异侧的情况,教师应予以肯定,如果没有学生画出,教师再引导指出) 画法二:画射线AO,BO,CO;沿着射线AO,BO,CO反方向上分别取点D,E,F,OD=2OA,OE=2OB,OF=2OC;顺次连结D,E,F,使△DEF与△ABC位似,相似比为2。 【探究2】 做一做: 利用下面的方法可以近似地将一个图形放大: 1.将两根长短相同的橡皮筋系在一起,联结处形成一个结点。 2.选取一个图形,在图形外取一个定点。 3.将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端。 4.拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘移动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形。 这个新图形与已知图形形状相同。 教师活动:同学们能用这种方法将一个已知图形放大吗?自己动手试一试,与同伴交流。 呈现了两个具有特殊位置关系的相似五边形,让学生再次感受位似图形的特点。在此基础上引出位似多边形的有关概念。 通过问题的形式,指导学生进行归纳总结,提高学生参与数学学习的意识,培养学生发现、概括的能力。 对知识进行巩练习,使学生对知队加深理解,便于教师及时了解学生对本节课内容的掌握情况。培养学生应用所学知识解决问题的能力。 拓展学生的思路,给出一种放大或缩小不规则图形的方法,同时让学生通过学习、思考、讨论,加深对前面知识的理解,感悟各种不同方法之间的内在联系。
3.学以致用,应用新知 考点1 位似多边形的概念 例1 下列各选项的两个图形中,是位似图形的个数为( ) A. 2 B. 3 C. 4 D. 1 答案:B 变式训练 下列各组图形中的两个三角形均满足△ABC∽△DEF,这两个三角形不是位似图形的是( ) 答案:B 考点2 位似多边形的性质 例2 如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=3OB,则△ABC与△DEF的周长之比是( ) A. 1∶2 B. 1∶4 C. 1∶3 D. 1∶9 答案:C 变式训练 如图,以点O为位似中心,把△ABC放大到原来的2倍得到△A′B′C′,以下说法中错误的是( ) A. △ABC∽△A′B′C′ B. 点A,O,A′三点在同一条直线上 C. AO∶AA′ D. S△ABC∶S△A′B′C′=1∶4 答案:C 考点3 位似多边形的画法 例3 课堂上数学老师让同学们完成“以点O为位似中心,将△ABC扩大到原来的两倍得到△A′B′C′,画出一个符合条件的△A′B′C′”的作图题,小明和小刚率先完成,他们的作图如下,则( ) A. 小明正确,小刚错误 B. 小明错误,小刚正确 C. 两人的作图都正确 D. 两人的作图都错误 答案:C 变式训练 如图,△ABC的顶点和定点O都在单位长度为1的正方形网格的格点上。以点O为位似中心,在网格纸中画出△ABC的位似△A′B′C′,使它与△ABC的相似比为2,且位于点O的右侧。 解: 通过例题的讲解,巩固学生理解位似多边形的概念,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生应用位似多边形的性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过例题的讲解,巩固学生掌握位似多边形的画法,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
4.随堂训练,巩固新知 1. “标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形( ) A. 左上 B. 左下 C. 右上 D. 右下 答案:B 2. 如图,位似图形由三角尺与其灯光照射下的影子组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为( ) A. 8 cm B. 20 cm C. 3.2 cm D. 10 cm 答案:B 3. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( ) A. 1∶2 B. 1∶4 C. 1∶5 D. 1∶6 答案:B 4. 用作位似图形的方法,可以将一个图形放大或缩小,位似中心位置可选在( ) A. 原图形的外部 B. 原图形的内部 C. 原图形的边上 D. 任意位置 答案:D 5. 如图所示,△ABC与△A′B′C′关于点O位似,BO=3,B′O=6。 (1)若AC=5,求A′C′的长; (2)若△ABC的面积为7,求△A′B′C′的面积。 解:(1)∵△ABC与△A′B′C′是位似图形,位似比为OB∶OB′=3∶6=1∶2, ∴=,即=, ∴A′C′=10。 (2)根据题意,得==, 即=,所以S△A′B′C′=7×4=28。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1.一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一个点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O称为位似中心。实际上,k就是这两个相似多边形的相似比。 2.两个位似图形的位似中心有且只有一个;位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处。 3.位似多边形的画法 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P115习题4.13中的T1、T2、T3、T4。 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 图形的位似 1.位似多边形的概念及其性质 2.位似多边形的画法 提纲掣领,重点突出。
教后反思 位似是相似图形的延伸和深化。经历位似图形的探索过程,进一步发展学生的探究、交流能力,培养学生动手操作的能力,体验学习的乐趣.位似图形在实际生产和生活中有着广泛的应用,通过现实情境,进一步发展学生从数学角度提出问题、分析问题、解决问题的能力,培养学生的数学应用意识,体会数学与自然、社会的联系。 反思,更进一步提升。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
