1.1.2 锐角三角函数 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 1.1.2 锐角三角函数 教学设计(表格式)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:36:06 | ||
图片预览



文档简介
1 锐角三角函数 第2课时
课题 锐角三角函数(第2课时) 授课类型 新授课
授课人
教学内容 课本P1-27
教学目标 1.经历探索直角三角形中边角关系的过程。 2.理解锐角三角函数正弦、余弦的意义,并能够举例说明。 3.能够运用cos A,sin A表示直角三角形中两边的比。 4.能够根据直角三角形中的边角关系,进行简单的计算。
教学重难点 重点:理解正弦、余弦的概念。 难点:用函数观点理解正弦、余弦,并用它来解决生活中的实际问题。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.复习回顾,导入新课 教师:通过上节课的学习,我们知道刻画梯子倾斜程度的方法一共有几种? 学生:有两种。一种是用梯子的倾斜角来刻画梯子的倾斜程度,一种是用倾斜角的正切来刻画梯子的倾斜程度。 教师:很好!在上节课的学习中,我们得出当倾斜角一定时,倾斜角的对边和邻边的比值也就随之确定,即这一比值只与倾斜角的大小有关,与直角三角形的大小无关。并在此基础上用直角三角形中锐角的对边与邻边之比定义了正切。那么还有没有其他方法来刻画梯子的倾斜程度呢 今天,我们就对这个问题继续进行深入研究。(板书课题:锐角三角函数 第2课时) 教师出示问题,学生回答,然后教师引出课题。 创设有意义的问题情境,调动学生学习积极性,让学生感受到倾斜程度在生活中的随处可见,并可以用数学模型来描述。
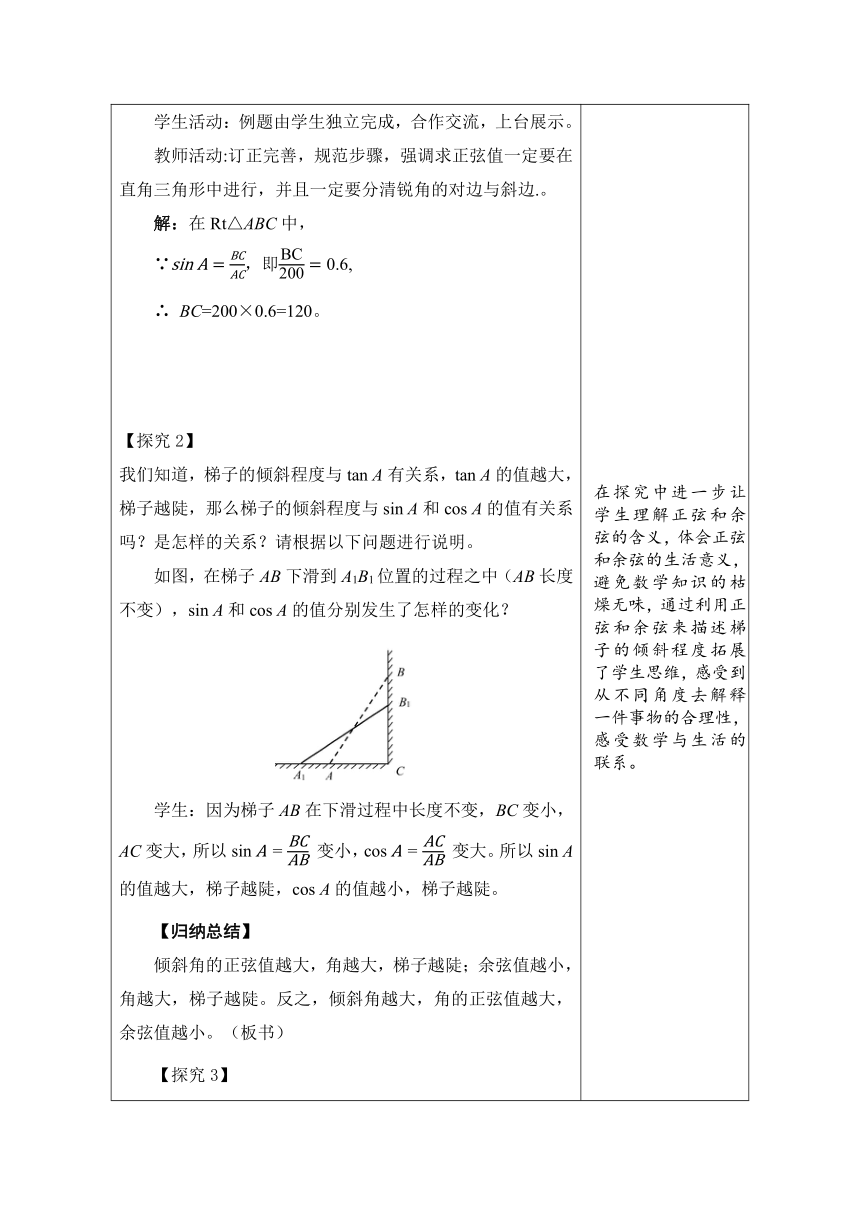
2.实践探究,学习新知 【探究1】 我们知道,当Rt△ABC中的锐角A确定时,∠A的对边与邻边的比便随之确定,此时其它边之间的比值也确定吗 (多媒体呈现) 学生:当Rt△ABC中的锐角A确定时,其它边之间的比值也确定。 教师:为什么?可以说下理由吗? 学生:因为任意两个直角三角形,当其中有一个锐角相等时,这两个三角形一定相似,所以其它边之间的比值也同对边和邻边的比值一样,是确定的。 教师(引入概念):非常好,在Rt△ABC中,如果锐角A确定,那么不仅∠A的对边与邻边的比是确定的,其他边的比值也是确定的。 此时,我们把∠A的对边BC与斜边AB的比叫做∠A的正弦,记作sin A,即; 把∠A的邻边AC与斜边AB的比叫做∠A的余弦,记作cos A,即。(多媒体呈现或板书正、余弦公式) 把锐角A的正弦,余弦,正切和余切都叫做∠A的三角函数。 教师:同学们还记得我们上节课学习正切时,对于正切有哪些要注意的吗? 学生:(1)tan A中常省略角的符号“∠”; (2)用希腊字母表示角时也可省略“∠”,如:tan α,tan β等; (3)用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成tan∠BAC或tan∠1,tan∠2等; t(4)an A是一个完的整数学符号,不可分割,不表示“tan”乘“A”。 教师追问:很好,其实正弦和余弦需要注意的问题同正切一样,同学们可以类比正切所注意的问题,尝试归纳下正弦和余弦需要注意的问题吗? 学生:(1)sin A,cos A中常省略角的符号“∠”。 (2)用希腊字母表示角时也可省略“∠”,如:sin α,cos β等; (3)用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成sin∠BAC或cos∠BAC,sin∠1,sin∠2等; (4)tan A是一个完的整数学符号,不可分割,不表示“tan”乘“A”。 教师:非常好。 师生活动:教师提问,学生思考讨论,最后由学生上台板书,教师查缺补漏。 【教材例题】 例 如图,在Rt△ABC中,∠B=90°,AC=200, sin A=0.6,求BC的长。 学生活动:例题由学生独立完成,合作交流,上台展示。 教师活动:订正完善,规范步骤,强调求正弦值一定要在直角三角形中进行,并且一定要分清锐角的对边与斜边.。 解:在Rt△ABC中, ∵,即, ∴ BC=200×0.6=120。 【探究2】 我们知道,梯子的倾斜程度与tan A有关系,tan A的值越大,梯子越陡,那么梯子的倾斜程度与sin A和cos A的值有关系吗?是怎样的关系?请根据以下问题进行说明。 如图,在梯子AB下滑到A1B1位置的过程之中(AB长度不变),sin A和cos A的值分别发生了怎样的变化? 学生:因为梯子AB在下滑过程中长度不变,BC变小,AC变大,所以 变小, 变大。所以sin A的值越大,梯子越陡,cos A的值越小,梯子越陡。 【归纳总结】 倾斜角的正弦值越大,角越大,梯子越陡;余弦值越小,角越大,梯子越陡。反之,倾斜角越大,角的正弦值越大,余弦值越小。(板书) 【探究3】 教师:如图,在Rt△ABC中,∠C=90°,有同学可以用三角形的边将sin A,sin B和cos A,cos B分别表示出来吗? 学生:, ,,。 教师追问:同学们,仔细观察,在Rt△ABC中,sin A和cos B,sin B和cos A之间分别存在什么数量关系? 学生:相等。 教师:也就是说,在直角三角形中,一个锐角的正弦值等于另一个锐角的余弦值。延伸一下,因为锐角的三角函数值只与锐角的大小有关,所以,只要两个锐角互余,那么其中一个锐角的正弦值,就一定等于另一个锐角的余弦值。(板书,几何语言表示) 做一做 如图,在Rt△ABC中,∠C=90°,AC=10,cos A=,求AB的长及sin B. 解:在Rt△ABC中, ∵cos A=, 即=,∴AB=。 ∴sinB==cosA=。
3.学以致用,应用新知 考点1 已知边长求三角函数值 P6 随堂练习1 变式训练 如图,某厂房屋顶呈人字架形(等腰三角形),已知AC=8,DB=4,CD⊥AB于点D,求sin B的值. 解:∵△ABC是等腰三角形,∴BC=AC=8. ∵CD⊥AB, ∴∠CDB=90°, ∴CD===4, ∴sin B===. 考点2 已知三角函数值求边长 P6 随堂练习2 变式训练 在Rt△ABC中,∠C=90°,AC=6,sinA,则AB的值为( ) A.8 B.9 C.10 D.7.5 答案:C 在例题讲解的基础上,通过基本的练习,以及对应的变式训练,进一步加强学生对正切和坡度的理解,形成相应的技能。
4.随堂训练,巩固新知 1. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则cos A的值是( ) A. B. C. D. 答案:D 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c。则下列各式中,正确的是( ) A. B. C. D. 答案:C 一等腰三角形的两边长分别为4 cm和6 cm,则其底角的余弦值为 . 答案:或 如图,在5×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是 . 答案: 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 1.理解了正弦和余弦的概念; 2.探索了正弦值、余弦值与梯子倾斜程度的关系,即倾斜角的正弦值越大,角越大,梯子越陡;余弦值越小,角越大,梯子越陡; 3.了解了互余的两锐角的三角函数的关系; 4.知道了在用三角函数解决一般三角形或四边形的实际问题中,应注意构造直角三角形。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:习题1.2 第1,2,3,4题; 2.弹性作业:习题1.2 第5题。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 锐角三角函数(第2课时)正弦、余弦的概念 正弦、余弦与梯子倾斜程度 互余两锐角的三角函数教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 由于上节课学生学习了三角函数中的正切,所以本节课引导学生进行类比学习,唤起和加深学生对教学内容的体会和了解,相对容易地掌握正弦和余弦的概念和意义。同时,探究活动培养和发展了学生的观察、思维能力。 本课时贯彻“从生动的直观到抽象的思维,并从抽象的思维到实践”的基本认识规律,运用直观教学,使学生易于理解正弦、余弦和角度之间的关系,以及两锐角的正弦、余弦值之间的关系。在学习新知的同时,完成了知识的巩固与内化。 反思,更进一步提升。
课题 锐角三角函数(第2课时) 授课类型 新授课
授课人
教学内容 课本P1-27
教学目标 1.经历探索直角三角形中边角关系的过程。 2.理解锐角三角函数正弦、余弦的意义,并能够举例说明。 3.能够运用cos A,sin A表示直角三角形中两边的比。 4.能够根据直角三角形中的边角关系,进行简单的计算。
教学重难点 重点:理解正弦、余弦的概念。 难点:用函数观点理解正弦、余弦,并用它来解决生活中的实际问题。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.复习回顾,导入新课 教师:通过上节课的学习,我们知道刻画梯子倾斜程度的方法一共有几种? 学生:有两种。一种是用梯子的倾斜角来刻画梯子的倾斜程度,一种是用倾斜角的正切来刻画梯子的倾斜程度。 教师:很好!在上节课的学习中,我们得出当倾斜角一定时,倾斜角的对边和邻边的比值也就随之确定,即这一比值只与倾斜角的大小有关,与直角三角形的大小无关。并在此基础上用直角三角形中锐角的对边与邻边之比定义了正切。那么还有没有其他方法来刻画梯子的倾斜程度呢 今天,我们就对这个问题继续进行深入研究。(板书课题:锐角三角函数 第2课时) 教师出示问题,学生回答,然后教师引出课题。 创设有意义的问题情境,调动学生学习积极性,让学生感受到倾斜程度在生活中的随处可见,并可以用数学模型来描述。
2.实践探究,学习新知 【探究1】 我们知道,当Rt△ABC中的锐角A确定时,∠A的对边与邻边的比便随之确定,此时其它边之间的比值也确定吗 (多媒体呈现) 学生:当Rt△ABC中的锐角A确定时,其它边之间的比值也确定。 教师:为什么?可以说下理由吗? 学生:因为任意两个直角三角形,当其中有一个锐角相等时,这两个三角形一定相似,所以其它边之间的比值也同对边和邻边的比值一样,是确定的。 教师(引入概念):非常好,在Rt△ABC中,如果锐角A确定,那么不仅∠A的对边与邻边的比是确定的,其他边的比值也是确定的。 此时,我们把∠A的对边BC与斜边AB的比叫做∠A的正弦,记作sin A,即; 把∠A的邻边AC与斜边AB的比叫做∠A的余弦,记作cos A,即。(多媒体呈现或板书正、余弦公式) 把锐角A的正弦,余弦,正切和余切都叫做∠A的三角函数。 教师:同学们还记得我们上节课学习正切时,对于正切有哪些要注意的吗? 学生:(1)tan A中常省略角的符号“∠”; (2)用希腊字母表示角时也可省略“∠”,如:tan α,tan β等; (3)用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成tan∠BAC或tan∠1,tan∠2等; t(4)an A是一个完的整数学符号,不可分割,不表示“tan”乘“A”。 教师追问:很好,其实正弦和余弦需要注意的问题同正切一样,同学们可以类比正切所注意的问题,尝试归纳下正弦和余弦需要注意的问题吗? 学生:(1)sin A,cos A中常省略角的符号“∠”。 (2)用希腊字母表示角时也可省略“∠”,如:sin α,cos β等; (3)用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成sin∠BAC或cos∠BAC,sin∠1,sin∠2等; (4)tan A是一个完的整数学符号,不可分割,不表示“tan”乘“A”。 教师:非常好。 师生活动:教师提问,学生思考讨论,最后由学生上台板书,教师查缺补漏。 【教材例题】 例 如图,在Rt△ABC中,∠B=90°,AC=200, sin A=0.6,求BC的长。 学生活动:例题由学生独立完成,合作交流,上台展示。 教师活动:订正完善,规范步骤,强调求正弦值一定要在直角三角形中进行,并且一定要分清锐角的对边与斜边.。 解:在Rt△ABC中, ∵,即, ∴ BC=200×0.6=120。 【探究2】 我们知道,梯子的倾斜程度与tan A有关系,tan A的值越大,梯子越陡,那么梯子的倾斜程度与sin A和cos A的值有关系吗?是怎样的关系?请根据以下问题进行说明。 如图,在梯子AB下滑到A1B1位置的过程之中(AB长度不变),sin A和cos A的值分别发生了怎样的变化? 学生:因为梯子AB在下滑过程中长度不变,BC变小,AC变大,所以 变小, 变大。所以sin A的值越大,梯子越陡,cos A的值越小,梯子越陡。 【归纳总结】 倾斜角的正弦值越大,角越大,梯子越陡;余弦值越小,角越大,梯子越陡。反之,倾斜角越大,角的正弦值越大,余弦值越小。(板书) 【探究3】 教师:如图,在Rt△ABC中,∠C=90°,有同学可以用三角形的边将sin A,sin B和cos A,cos B分别表示出来吗? 学生:, ,,。 教师追问:同学们,仔细观察,在Rt△ABC中,sin A和cos B,sin B和cos A之间分别存在什么数量关系? 学生:相等。 教师:也就是说,在直角三角形中,一个锐角的正弦值等于另一个锐角的余弦值。延伸一下,因为锐角的三角函数值只与锐角的大小有关,所以,只要两个锐角互余,那么其中一个锐角的正弦值,就一定等于另一个锐角的余弦值。(板书,几何语言表示) 做一做 如图,在Rt△ABC中,∠C=90°,AC=10,cos A=,求AB的长及sin B. 解:在Rt△ABC中, ∵cos A=, 即=,∴AB=。 ∴sinB==cosA=。
3.学以致用,应用新知 考点1 已知边长求三角函数值 P6 随堂练习1 变式训练 如图,某厂房屋顶呈人字架形(等腰三角形),已知AC=8,DB=4,CD⊥AB于点D,求sin B的值. 解:∵△ABC是等腰三角形,∴BC=AC=8. ∵CD⊥AB, ∴∠CDB=90°, ∴CD===4, ∴sin B===. 考点2 已知三角函数值求边长 P6 随堂练习2 变式训练 在Rt△ABC中,∠C=90°,AC=6,sinA,则AB的值为( ) A.8 B.9 C.10 D.7.5 答案:C 在例题讲解的基础上,通过基本的练习,以及对应的变式训练,进一步加强学生对正切和坡度的理解,形成相应的技能。
4.随堂训练,巩固新知 1. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则cos A的值是( ) A. B. C. D. 答案:D 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c。则下列各式中,正确的是( ) A. B. C. D. 答案:C 一等腰三角形的两边长分别为4 cm和6 cm,则其底角的余弦值为 . 答案:或 如图,在5×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是 . 答案: 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 1.理解了正弦和余弦的概念; 2.探索了正弦值、余弦值与梯子倾斜程度的关系,即倾斜角的正弦值越大,角越大,梯子越陡;余弦值越小,角越大,梯子越陡; 3.了解了互余的两锐角的三角函数的关系; 4.知道了在用三角函数解决一般三角形或四边形的实际问题中,应注意构造直角三角形。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:习题1.2 第1,2,3,4题; 2.弹性作业:习题1.2 第5题。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 锐角三角函数(第2课时)正弦、余弦的概念 正弦、余弦与梯子倾斜程度 互余两锐角的三角函数教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 由于上节课学生学习了三角函数中的正切,所以本节课引导学生进行类比学习,唤起和加深学生对教学内容的体会和了解,相对容易地掌握正弦和余弦的概念和意义。同时,探究活动培养和发展了学生的观察、思维能力。 本课时贯彻“从生动的直观到抽象的思维,并从抽象的思维到实践”的基本认识规律,运用直观教学,使学生易于理解正弦、余弦和角度之间的关系,以及两锐角的正弦、余弦值之间的关系。在学习新知的同时,完成了知识的巩固与内化。 反思,更进一步提升。
