1.4 解直角三角形 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 1.4 解直角三角形 教学设计(表格式)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 647.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:36:35 | ||
图片预览


文档简介
4 解直角三角形
课题 解直角三角形 授课类型 新授课
授课人
教学内容 课本P16-18
教学目标 1.了解解直角三角形的含义。 2.经历解直角三角形的过程, 掌握解直角三角形的方法。
教学重难点 重点:理解并掌握直角三角形边角之间的关系,运用直角三角形的两锐角互余、勾股定理及锐角三角函数求直角三角形的未知元素。 难点:从已知条件出发,正确选用适当的边角关系或三角函数解题。
教学准备 多媒体课件、三角尺、直尺。
教与学互动设计(教学过程) 设计意图
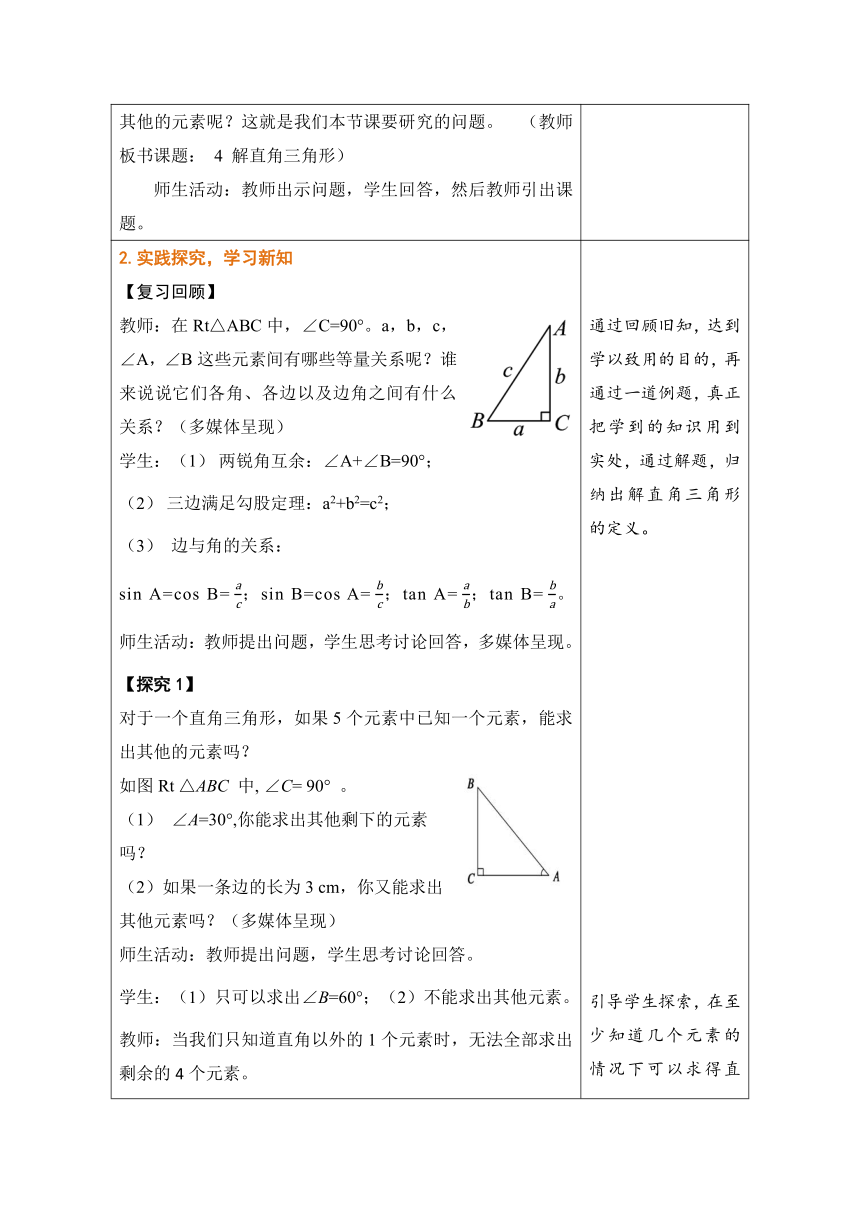
1.创设情景,导入新课 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.如图,现有一个长6 m的梯子,问: (1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1 m)? (2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子? 学生:解:(1)由题意,得6×sin75°≈5.8 m。 (2)由题意,得cos α==0.4,cos 0.4≈66°。可以安全使用。 教师:在图形的研究中,直角三角形是常见的三角形之一,因而人们经常会遇到求直角三角形的边长或角度等问题。为了解决这些问题,则往往需要确定直角三角形的边或角。 我们知道,直角三角形有三条边和三个角,一共6个元素,那么除直角以外,当我们至少知道几个元素时,就可以求出其他的元素呢?这就是我们本节课要研究的问题。 (教师板书课题: 4 解直角三角形) 师生活动:教师出示问题,学生回答,然后教师引出课题。 体会数学知识来源于生活,激发学生的学习兴趣,由此引入对解直角三角形的探究.
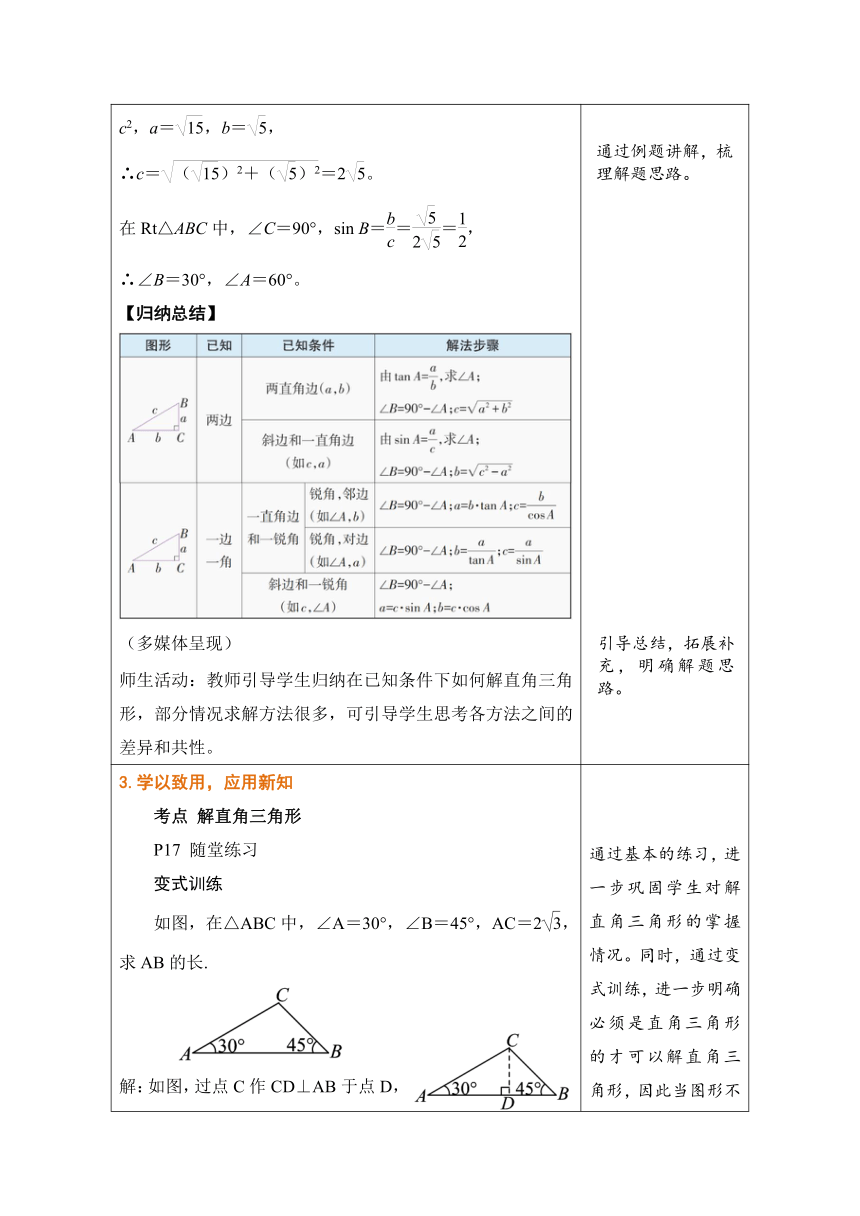
2.实践探究,学习新知 【复习回顾】 教师:在Rt△ABC中,∠C=90°。a,b,c,∠A,∠B这些元素间有哪些等量关系呢?谁来说说它们各角、各边以及边角之间有什么关系?(多媒体呈现) 学生:(1) 两锐角互余:∠A+∠B=90°; (2) 三边满足勾股定理:a2+b2=c2; (3) 边与角的关系: sin A=cos B= ;sin B=cos A= ;tan A= ;tan B= 。 师生活动:教师提出问题,学生思考讨论回答,多媒体呈现。 【探究1】 对于一个直角三角形,如果5个元素中已知一个元素,能求出其他的元素吗? 如图Rt △ABC 中, ∠C= 90° 。 (1) ∠A=30°,你能求出其他剩下的元素吗? (2)如果一条边的长为3 cm,你又能求出其他元素吗?(多媒体呈现) 师生活动:教师提出问题,学生思考讨论回答。 学生:(1)只可以求出∠B=60°;(2)不能求出其他元素。 教师:当我们只知道直角以外的1个元素时,无法全部求出剩余的4个元素。 【探究2】 如果5个元素中已知两个元素,能求出其他的元素吗? 在Rt△ABC中, (1)根据AC=,BC=,你能求出这个三角形的其他元素吗? (2)根据∠A= 60°,斜边AB=30,你能求出这个三角形的其他元素吗 (3)根据∠A=60°,∠B=30°, 你能求出这个三角形的其他元素吗 (多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师引导讲解。 学生:(1)能。在Rt△ABC中,∵AB2=AC2+BC2,AC=,BC=,∴AB=。在Rt△ABC中,,∴∠A=60°,∠B=30°。 (2)能。在Rt△ABC中,∠C=90°,∠A=60°,∴∠B=30°。 ∵,AB=30,∴BC=ABsin A=。 ∵,AB=30,∴AC=ABsin B=。 (3)不能求出三角形的边长。 教师(概念引入):我们可以发现,在直角三角形中,只要知道其中两个元素(至少有一个是边)就可以求出其余的几个元素,像这样的,由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形。 【例题讲解】 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=,b=,求这个三角形的其他元素. 师生活动:学生思考解题,板书呈现,教师补充讲解。 解:在Rt△ABC中,∠C=90°,根据勾股定理,得a2+b2=c2,a=,b=, ∴c==2。 在Rt△ABC中,∠C=90°,sin B===, ∴∠B=30°,∠A=60°。 【归纳总结】 (多媒体呈现) 师生活动:教师引导学生归纳在已知条件下如何解直角三角形,部分情况求解方法很多,可引导学生思考各方法之间的差异和共性。 通过回顾旧知,达到学以致用的目的,再通过一道例题,真正把学到的知识用到实处,通过解题,归纳出解直角三角形的定义。 引导学生探索,在至少知道几个元素的情况下可以求得直角三角形中的剩余元素(解直角三角形),进而引出解直角三角形的概念。
3.学以致用,应用新知 考点 解直角三角形 P17 随堂练习 变式训练 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长. 解:如图,过点C作CD⊥AB于点D, ∴∠ADC=∠BDC=90°. ∵∠B=45°, ∴∠BCD=∠B=45°,∴CD=BD。 ∵∠A=30°,AC=2,∴CD=,∴BD=CD=。 由勾股定理得,AD==3,∴AB=AD+BD=3+。 【拓展延伸】(多媒体呈现、教师讲解) 常见的做辅助线构造直角三角形的方法 三角形内部作辅助线(背靠背型) 背靠背型 平移变形 旋转变形 模型特点:三角形三个内角分别是:两个特殊角以及一个合角。(特殊角指已知三角函数值的角,合角指由两个特殊角组合成的角) 辅助线的常用做法:在三角形内部,过特殊角的合角的顶点作高,构造两个直角三角形. 三角形外部作辅助线(母子型) 母子型 平移变形 平移变形 旋转变形 旋转→平移变形 模型特点:三角形的三个内角分别是:一个特殊角、一个特殊角的补角以及一个差角.(差角指由两个特殊角作差形成的角) 辅助线的常用做法:在三角形外部,过特殊角的差角的顶点作高,构造两个直角三角形. 通过基本的练习,进一步巩固学生对解直角三角形的掌握情况。同时,通过变式训练,进一步明确必须是直角三角形的才可以解直角三角形,因此当图形不是直角三角形时,应当首先构建直角三角形。 拓展延伸
4.随堂训练,巩固新知 1. 已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么( ) A.BC=10cos 50° B.BC=10sin 50° C.AC=10tan 50° D.AC=10cos 50° 答案:A 如图,在△ABC中,tan B=1,sin C,AB,则边BC的长为( ) A. B. C. D. 答案:B 如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则tan∠AED的值为( ) A. B. C.2 D.2 答案:C 如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cos A的值. 解:在Rt△ABC中,∠C=90°,由勾股定理可知:BC5,cos A。 “木楔”是指木材制作的楔形物,它能够使榫卯配合的牢固程度最大化,如图1,是木工制作中一种叫做楔钉榫的补强方式,其所用木楔的截面图如图2所示,若 已 测 ∠C=90° ,∠B=25° ,AC=10 cm,则AB,BC的长度是多少?(结果精确到0.1 cm) (参考数据:sin 25°≈0.42,cos 25°≈0.91, tan 25°≈0.47) 解:在Rt△ABC中,∠C=90°, sin 25°,tan 25°, ∴AB≈23.8(cm), BC≈21.3(cm), ∴AB长23.8 cm,BC长21.3 cm。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1. 直角三角形中边与边、角与角、边与角的关系(基础)。 2. 解直角三角形定义。 3. 解直角三角形的方法(重点) 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P17 习题1.5 第1,2,3题。 课后练习巩固,让学生所学知识得以运用,提高解直角三角形的能力。
板书设计 4 解直角三角形一、解直角三角形教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课,为解直角三角形应用题之前的准备课,旨在建立好解直角三角形的数学模型,以便有效的为现实生活服务。培养学生解答实际应用题的技能,掌握如何构建解直角三角形的思想方法、技巧。把勾股定理和锐角三角函数的前期准备知识有机的组织起来,使学生能承前启后、有思想性和可操作性。因此,本节课在教材教学计划中起着一发牵制全局的重要作用。 本节课由生活中的实际问题引出课题,激发了学生学习数学的积极性。同时通过通过师生互动的教学形式,归纳出只有具有至少一边的两个条件,可解直角三角形,以及直角三角形的基本类型和解法。同时为了深化知识,设计变式训练,提高学生的解题能力。 反思,更进一步提升。
课题 解直角三角形 授课类型 新授课
授课人
教学内容 课本P16-18
教学目标 1.了解解直角三角形的含义。 2.经历解直角三角形的过程, 掌握解直角三角形的方法。
教学重难点 重点:理解并掌握直角三角形边角之间的关系,运用直角三角形的两锐角互余、勾股定理及锐角三角函数求直角三角形的未知元素。 难点:从已知条件出发,正确选用适当的边角关系或三角函数解题。
教学准备 多媒体课件、三角尺、直尺。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.如图,现有一个长6 m的梯子,问: (1)使用这个梯子最高可以安全攀上多高的墙(精确到0.1 m)? (2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角α等于多少(精确到1°)?这时人是否能够安全使用这个梯子? 学生:解:(1)由题意,得6×sin75°≈5.8 m。 (2)由题意,得cos α==0.4,cos 0.4≈66°。可以安全使用。 教师:在图形的研究中,直角三角形是常见的三角形之一,因而人们经常会遇到求直角三角形的边长或角度等问题。为了解决这些问题,则往往需要确定直角三角形的边或角。 我们知道,直角三角形有三条边和三个角,一共6个元素,那么除直角以外,当我们至少知道几个元素时,就可以求出其他的元素呢?这就是我们本节课要研究的问题。 (教师板书课题: 4 解直角三角形) 师生活动:教师出示问题,学生回答,然后教师引出课题。 体会数学知识来源于生活,激发学生的学习兴趣,由此引入对解直角三角形的探究.
2.实践探究,学习新知 【复习回顾】 教师:在Rt△ABC中,∠C=90°。a,b,c,∠A,∠B这些元素间有哪些等量关系呢?谁来说说它们各角、各边以及边角之间有什么关系?(多媒体呈现) 学生:(1) 两锐角互余:∠A+∠B=90°; (2) 三边满足勾股定理:a2+b2=c2; (3) 边与角的关系: sin A=cos B= ;sin B=cos A= ;tan A= ;tan B= 。 师生活动:教师提出问题,学生思考讨论回答,多媒体呈现。 【探究1】 对于一个直角三角形,如果5个元素中已知一个元素,能求出其他的元素吗? 如图Rt △ABC 中, ∠C= 90° 。 (1) ∠A=30°,你能求出其他剩下的元素吗? (2)如果一条边的长为3 cm,你又能求出其他元素吗?(多媒体呈现) 师生活动:教师提出问题,学生思考讨论回答。 学生:(1)只可以求出∠B=60°;(2)不能求出其他元素。 教师:当我们只知道直角以外的1个元素时,无法全部求出剩余的4个元素。 【探究2】 如果5个元素中已知两个元素,能求出其他的元素吗? 在Rt△ABC中, (1)根据AC=,BC=,你能求出这个三角形的其他元素吗? (2)根据∠A= 60°,斜边AB=30,你能求出这个三角形的其他元素吗 (3)根据∠A=60°,∠B=30°, 你能求出这个三角形的其他元素吗 (多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师引导讲解。 学生:(1)能。在Rt△ABC中,∵AB2=AC2+BC2,AC=,BC=,∴AB=。在Rt△ABC中,,∴∠A=60°,∠B=30°。 (2)能。在Rt△ABC中,∠C=90°,∠A=60°,∴∠B=30°。 ∵,AB=30,∴BC=ABsin A=。 ∵,AB=30,∴AC=ABsin B=。 (3)不能求出三角形的边长。 教师(概念引入):我们可以发现,在直角三角形中,只要知道其中两个元素(至少有一个是边)就可以求出其余的几个元素,像这样的,由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形。 【例题讲解】 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a=,b=,求这个三角形的其他元素. 师生活动:学生思考解题,板书呈现,教师补充讲解。 解:在Rt△ABC中,∠C=90°,根据勾股定理,得a2+b2=c2,a=,b=, ∴c==2。 在Rt△ABC中,∠C=90°,sin B===, ∴∠B=30°,∠A=60°。 【归纳总结】 (多媒体呈现) 师生活动:教师引导学生归纳在已知条件下如何解直角三角形,部分情况求解方法很多,可引导学生思考各方法之间的差异和共性。 通过回顾旧知,达到学以致用的目的,再通过一道例题,真正把学到的知识用到实处,通过解题,归纳出解直角三角形的定义。 引导学生探索,在至少知道几个元素的情况下可以求得直角三角形中的剩余元素(解直角三角形),进而引出解直角三角形的概念。
3.学以致用,应用新知 考点 解直角三角形 P17 随堂练习 变式训练 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求AB的长. 解:如图,过点C作CD⊥AB于点D, ∴∠ADC=∠BDC=90°. ∵∠B=45°, ∴∠BCD=∠B=45°,∴CD=BD。 ∵∠A=30°,AC=2,∴CD=,∴BD=CD=。 由勾股定理得,AD==3,∴AB=AD+BD=3+。 【拓展延伸】(多媒体呈现、教师讲解) 常见的做辅助线构造直角三角形的方法 三角形内部作辅助线(背靠背型) 背靠背型 平移变形 旋转变形 模型特点:三角形三个内角分别是:两个特殊角以及一个合角。(特殊角指已知三角函数值的角,合角指由两个特殊角组合成的角) 辅助线的常用做法:在三角形内部,过特殊角的合角的顶点作高,构造两个直角三角形. 三角形外部作辅助线(母子型) 母子型 平移变形 平移变形 旋转变形 旋转→平移变形 模型特点:三角形的三个内角分别是:一个特殊角、一个特殊角的补角以及一个差角.(差角指由两个特殊角作差形成的角) 辅助线的常用做法:在三角形外部,过特殊角的差角的顶点作高,构造两个直角三角形. 通过基本的练习,进一步巩固学生对解直角三角形的掌握情况。同时,通过变式训练,进一步明确必须是直角三角形的才可以解直角三角形,因此当图形不是直角三角形时,应当首先构建直角三角形。 拓展延伸
4.随堂训练,巩固新知 1. 已知在△ABC中,∠C=90°,∠B=50°,AB=10,那么( ) A.BC=10cos 50° B.BC=10sin 50° C.AC=10tan 50° D.AC=10cos 50° 答案:A 如图,在△ABC中,tan B=1,sin C,AB,则边BC的长为( ) A. B. C. D. 答案:B 如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则tan∠AED的值为( ) A. B. C.2 D.2 答案:C 如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cos A的值. 解:在Rt△ABC中,∠C=90°,由勾股定理可知:BC5,cos A。 “木楔”是指木材制作的楔形物,它能够使榫卯配合的牢固程度最大化,如图1,是木工制作中一种叫做楔钉榫的补强方式,其所用木楔的截面图如图2所示,若 已 测 ∠C=90° ,∠B=25° ,AC=10 cm,则AB,BC的长度是多少?(结果精确到0.1 cm) (参考数据:sin 25°≈0.42,cos 25°≈0.91, tan 25°≈0.47) 解:在Rt△ABC中,∠C=90°, sin 25°,tan 25°, ∴AB≈23.8(cm), BC≈21.3(cm), ∴AB长23.8 cm,BC长21.3 cm。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1. 直角三角形中边与边、角与角、边与角的关系(基础)。 2. 解直角三角形定义。 3. 解直角三角形的方法(重点) 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P17 习题1.5 第1,2,3题。 课后练习巩固,让学生所学知识得以运用,提高解直角三角形的能力。
板书设计 4 解直角三角形一、解直角三角形教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课,为解直角三角形应用题之前的准备课,旨在建立好解直角三角形的数学模型,以便有效的为现实生活服务。培养学生解答实际应用题的技能,掌握如何构建解直角三角形的思想方法、技巧。把勾股定理和锐角三角函数的前期准备知识有机的组织起来,使学生能承前启后、有思想性和可操作性。因此,本节课在教材教学计划中起着一发牵制全局的重要作用。 本节课由生活中的实际问题引出课题,激发了学生学习数学的积极性。同时通过通过师生互动的教学形式,归纳出只有具有至少一边的两个条件,可解直角三角形,以及直角三角形的基本类型和解法。同时为了深化知识,设计变式训练,提高学生的解题能力。 反思,更进一步提升。
